基于灰狼算法的配电网短路故障自动监测系统

施晓敏，徐 飞，沈 磊

（国网安徽省电力有限公司，合肥 230022）

配电网在电力系统当中起着至关重要的作用，由于实际配电网运行过程中存在一定的噪声干扰等情况，导致故障识别的准确率与快捷性无法进一步提高[1-2]。基于此提出通过灰狼算法进行神经网络的优化，并结合集成经验模态进行本证模态分量的分解，以此构建相应的自动化监测系统，对故障线路进行自动化识别。

1 基于经验模态的电流暂态分解

短路接地的等效电路如图1 所示。

图1 短路接地等效暂态分析Fig.1 Equivalent transient analysis of short-circuit grounding

图1 中，C 为线路相应的对地电容；R0为等效后的等值电阻，该接地电阻包括发生故障时的电弧电阻以及接地电阻[3-5]；L0为未接地的中性点等效后的电感；L 为消弧线圈等效后的电感，对应等效电阻用RL表示；U0为零序电源对应的等效电压。

发生故障时电流的暂态可以描述为

式中：暂态电流由两部分组成，iC为一部分电容产生的电流，iL为一部分电感产生的电流；ICm为稳态情况下iC对应的幅值；ILm为iL对应的幅值；Um为零序电压对应的幅值；ω 为工频情况下对应的频率；φ 为电压的相位。电容回路中，τC为时间常数；电感回路中，τL为时间常数；无外界干扰时，ωf为电流振荡频率。其中接地电流时的稳态对应式（1）中的（ICm-ILm）·cos（ωt+φ），电容电流对应的直流部分对应式（1）中的，电感电流对应的直流部分对应式（1）中的ILmcosφe-t/τL，电容与电感电流的直流部分构成对应的暂态电流。

2 集成经验模态分解

2.1 集成经验模态概述

首先需要对输入的原始信号进行多次复制，得到原始信号相应的序列，而后加入相应的高斯白噪声，这一过程表述为

式中：ni（t）为相应的高斯白噪声；x（t）为原始信号。

在得到相应的集成经验模态原始信号的序列之后，对其进行经验模态的分解，将其表述为

式中：集成经验模态被分解为2 个部分，cij为信号i分解之后对应的经验模态分量j，ri为除去信号i 对应其余的残余分量。

依据上述步骤对整体经验模态进行分解，而后求对应的平均值，再进行经验模态分量以及残余分量的求和，将其表述为

式中：cj（t）为经验模态j，通过式（5）求取，相应的参与分量通过式（6）求取。

式中：M 为相应经验模态分量的个数。

2.2 提取数据特征

系统选择的采样频率为10 kHz，对故障后一工频周期进行数据采样，步长选择1 ms，滑动窗窗宽设置为5 ms。对于滑动窗，可以如下形式划分：

式中：ch为采样点，h=1，2，…，200；si为滑动窗，i=1，2，…，16。

对各窗口得到的波形数据通过集成经验模态做出分解，得到对应多个经验模态，对应分量的能量值可以表述为

式中：v 为对应分量k 不同的离散点；N 为采样点的总数；x 为对应窗口序列；y 为相应的线路。

3 灰狼算法寻优

3.1 改进循环神经网络

改进后循环神经网络的结构示意图如图2所示。

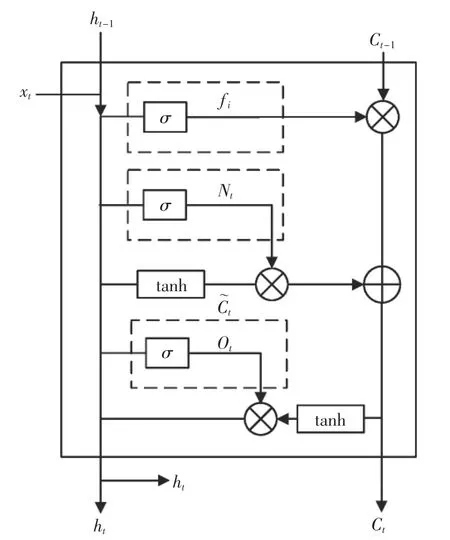
图2 改进神经网络结构示意图Fig.2 Schematic diagram of the improved neural network structure

图2 由下及上不同的虚线框分别对应输出门、输入门以及遗忘门。对于上一时刻，Ct-1、ht-1为相应的隐藏量，xt为时刻t 对应隐藏量，fi为遗忘门对应的输出，Nt为输入门对应的输入，为输入单元当前状态，Ot为输出门对应的输出，Ct和ht为时刻t对应的输出。

优化后仅设置重置门以及相应的更新门，对应的网络结构示意图如图3 所示。

图3 优化后网络结构示意图Fig.3 Schematic diagram of the optimized network structure

优化后神经网络的参数更新可以表示为

式中：rt为重置门；zt为更新门；xt为时刻t 对应的输入为对应的候选隐藏量；ht为隐藏量；wr、wz以及wh分别为不同的权重系数；σ（）为sigmoid 激活函数；tanh（）为双曲正切函数。

3.2 灰狼算法优化

灰狼算法以狼群为学习对象，设狼群中α 适应的能力最强，β 适应的能力仅次于α，σ 为其余适应能力的狼，3 种狼通过定位不断靠近猎物。

据此，狼群与猎物之间的初始距离可以表示为

式中：g 为迭代的次数；s 为狼的位置；sp为猎物对应位置；c 为不同类狼对应的权重系数；r1为随机数，范围是［0，1］。

初始距离确定之后，按照式（11）～式（14）进行距离以及适应度的更新。

式中：μ 为收敛向量；r2为随机数，范围是［0，1］；a随着迭代线性递减，初始值设为2；dk为狼群k 同猎物的距离；ci为不同狼对应的权重系数；μi为对应的收敛向量。

由此优化后的神经网络流程如图4 所示。

图4 灰狼算法优化神经网络流程Fig.4 Flow chart of grey wolf algorithm optimizes neural network

4 自动化监测模型构建

4.1 神经网络构建

优化后的神经网络如图5 所示。

图5 优化神经网络整体示意图Fig.5 Schematic diagram of the optimized neural network

图5 中，单独由灰狼算法优化后的神经网络难以具备较强的分类性能，加入对应的softmax 层以提高分类能力，Mi（i=0，1，…，n）为神经网络对应的输入层。

4.2 整体检测模型构建

基于灰狼算法优化神经网络的整体监测模型具体流程如图6 所示。

图6 自动化监测模型具体流程Fig.6 Flow chart of the automated monitoring model

5 实例验证及性能分析

5.1 自动化监测系统实例验证及分析

5.1.1 故障模型参数设置

系统仿真模型通过PSCAD 进行搭建，具体线路仿真如图7 所示，对应的线路参数如表1 所示。

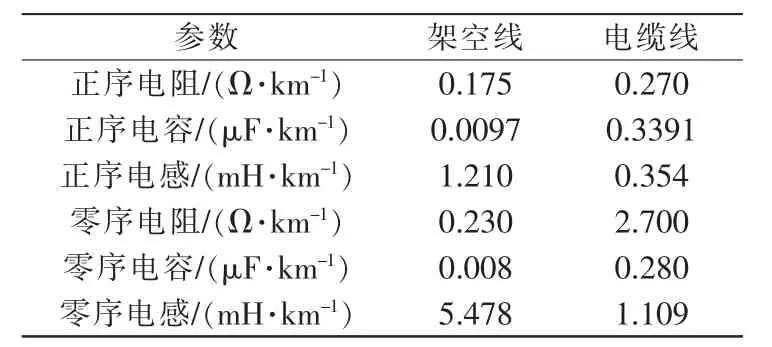
表1 线路参数设定Tab.1 Line parameter settings

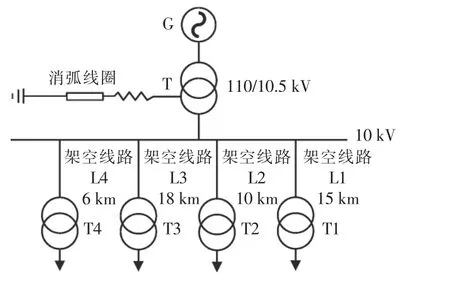
图7 实际线路仿真模型Fig.7 Actual line simulation model

故障设定为发生接地短路的线路为L2，得到对应的零序电流测试图如图8 所示。

图8 零序电流测试图Fig.8 Zero-sequence current test diagram

5.1.2 故障数据样本选择

故障样本数据选择接地短路故障时产生的零序电流的数据信息。首个滑动窗通过集成经验模态分解之后的示意图如图9 所示。

图9 集成经验模态分解滑动窗示意图Fig.9 Schematic diagram of integrated empirical mode decomposition sliding window

实际故障数据采集时，对接地电阻、初始角以及接地点进行不同设定，具体设定如表2 所示。

表2 中，依据不同的参数设定，在4 条线路当中可以生成720 组不同的样本数据信息。

5.1.3 故障检测分析测试

依据上述分组，选择640 组样本数据信息作为训练集数据，选择80 组数据作为测试数据，最终测试结果如图10 所示。

图10 最终测试结果对比Fig.10 Comparison of final test results

图10 中，实际测试结果与系统预测结果基本吻合。

实际配电网运行时，短路故障是随机的，为了真实模拟实际情况，对故障参数进行随机生成并分析，得到的结果如表3 所示。

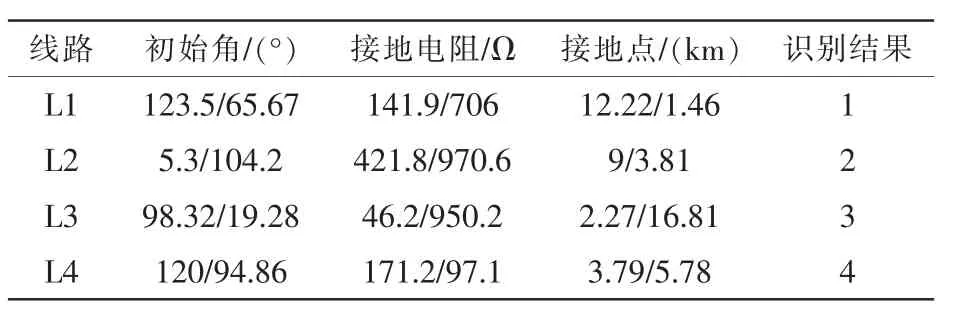
表3 随机故障测试结果Tab.3 Random fault test results

5.2 系统算法实例验证及分析

5.2.1 噪声干扰测试

当噪声干扰为10 dB 时，原始波形与噪声干扰图像如图11 所示。

图11 原始波形写噪声干扰波形示意图Fig.11 Schematic diagram of the original waveform and the noise interference waveform

分析图11 可知，当噪声干扰时，整体波形的变化幅度不大，仅在0.025 s 左右波形产生了较大幅度变化。对不同噪声干扰对比得测试结果如表4所示。

表4 不同噪声干扰测试结果对比Tab.4 Comparison of test results of different noise interference

表4 中，噪声干扰的识别率均在92.5%以上，且随着信噪比的增大，识别率相对变高。

5.2.2 随机数据信息丢失

实验测试选择L1 线路进行数据信息丢失测试，原始数据图像如图12 所示，数据丢失图像如图13 所示。

图12 未丢失数据原始图像Fig.12 Raw image of no data loss

图13 丢失部分数据图像Fig.13 Image of partial data loss

图12 与图13 中，当数据部分丢失时，与原始图像产生较大差别，具体的识别结果如图14 所示。

图14 实际改进算法测试结果Fig.14 Test results of the actual improved algorithm

图14 中，尽管在数据信息部分丢失的情况下波形差别相对较大，但改进算法依旧能够精确地识别到相应的故障线路。

5.2.3 不同神经网络对比测试

将灰狼优化后的神经网络与其他神经网络如RBF、Elman 以及BP 进行对比，得到的对比结果如表5 所示。表5 中，本文改进的神经网络在不同情况下均表现出优异的识别性能。

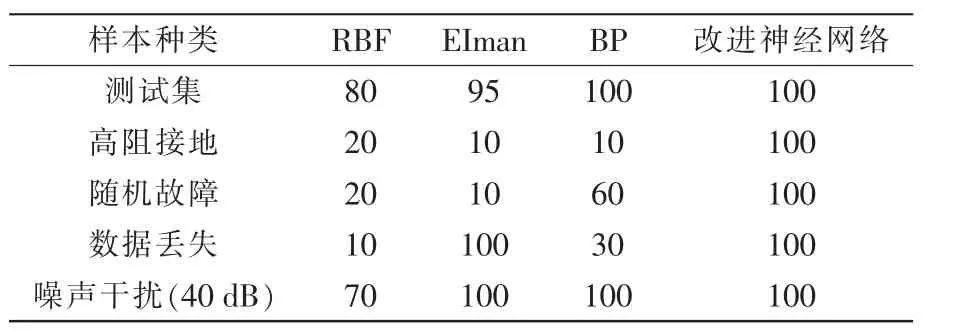
表5 不同神经网络对比结果/（%）Tab.5 Comparison results of different neural networks/（%）

6 结语

自动化监测系统中，通过灰狼算法对神经网络进行进一步的优化，同时结合集成经验模态进行暂态电流的分解，改进系统参数设置更少，同时优化相应的计算步骤。经过实际算例验证，提出的自动化监测系统能够在提高效率的同时，具备更好的抗干扰性能，相比其他算法具有更精确的识别率。