基于半解析涡环模型的农用单旋翼直升机流场快速计算

金济 薛新宇 姚伟祥

摘要：農业航空领域中，定量获取风场（流场）速度分布对单旋翼直升机辅助授粉作业、农药施用效率提升具有重要意义。基于此提出一种半解析理论方法能够快速完整计算单旋翼流场速度。以涡环模型为基础，将农用直升机旋转桨盘下的尾涡系等效为涡环连续叠加所形成的圆柱涡面，再由涡环速度诱导公式半解析计算直升机旋翼空间各点速度。理论模型与仿真和文献试验数据比较，结果表明：涡环模型简单快速，普通计算机（CPU 2 GHz，内存2 GB）上2.8 s完成计算；悬停时与计算流体力学仿真结果下洗速度径向平均误差小于1.9 m/s，平均相对误差小于39.1%，轴向平均误差小于2.26 m/s，平均相对误差小于54.6%；悬停时，诱速从中央往桨尖递增；前飞时，平飞速度越大诱速越小；流场主要影响因素依次为前飞速度、旋翼半径、飞机总重、空气密度。为定量计算农用直升机旋翼风场、辅助授粉作业和田间施药喷头布置提供一种快速方法和参考。

关键词：农用单旋翼直升机；流场计算；涡环模型；流场影响因素；农业航空

中图分类号：S252  文献标识码：A  文章编号：2095-5553 （2024） 03-0163-10

Fast computation of single-rotor helicopter flow field based on semi-analytic vortex ring model

Jin Ji1， Xue Xinyu 2， Yao Weixiang3

（1. College of Engineering， South China Agricultural University， Guangzhou， 510642， China; 2. Nanjing Institute ofAgricultural Mechanization， Ministry of Agriculture and Rural Affairs， Nanjing， 210014， China; 3. School ofInformation and Electrical Engineering， Shenyang Agricultural University， Shenyang， 110866， China）

Abstract：

In agricultural aviation， quantitative acquisition of wind field （flow field） velocity distribution is important for single-rotor helicopter-assisted pollination operations and pesticide application efficiency improvement. As a complement to the wind field computational fluid dynamics simulation， field or laboratory measurement methods， this paper applies a semi-analytical theoretical method to rapidly and completely calculate the single-rotor flow field velocity. Based on the vortex ring model， the trailing vortex by the tip of the helicopters high-speed rotating propeller is equated to a vortex ring， and the wake vortices system under the propeller disk is equated to a cylindrical vortex surface formed by the continuous superposition of vortex rings. The wake shape is judged according to the motion state， and the vortex ring position and radius are determined by the fixed wake or predetermined wake， and the velocity of each point in helicopter rotor space is calculated analytically or semi-analytically by the vortex ring velocity induction equation. The comparison of the theoretical model with the computational fluid dynamics simulation and literature test data shows that the vortex ring model is simple and fast， and the calculation is completed in 2.8 s on an ordinary computer （CPU 2 GHz， memory 2 GB）. The average error in radial direction is less than 1.71 m/s， the average relative error is less than 39.1%， the average error in axial direction is less than 2.26 m/s， and the average relative error is less than 54.6%. When hovering， the induced velocity increases from the center to the tip of the rotor. In forward flight， the higher the leveling speed， the lower the induced velocity， and the lower the forward flight speed， the airflow outside the slipstream below the rotor changes from upwash to horizontal flow to downwash. The main factors affecting the flow field are forward flight speed， rotor radius， gross weight of the aircraft， and air density in that order. This model and results can provide a quick method and reference for quantitative calculation of rotor wind field to assist pollination operation and field application nozzle arrangement.

Keywords：single-rotor helicopter; rotor flow field; vortex ring; impact factors of flow field； agricultural aviation

0 引言

农用单旋翼直升机广泛用于植保施药或植物辅助授粉作业。航空施药中的单旋翼尺度变化范围大，航速、航高、喷头数量等不尽相同，雾滴飘失程度也就相差较远［1， 2］。单旋翼直升机施药作业时应使雾滴进入尾迹，利用旋翼下洗气流使之准确快速接触植株冠层［3］。同样，直升机风场宽度、速度也对作物辅助授粉效果有重要影响［4］。故快速有效计算速度分布对掌握单旋翼风场（流场）规律，提高施药质量、提升授粉效果、降低飘失带来的环境污染具有重要意义。

研究旋翼流场有数值模拟［5］、理论分析［6］、实验室（含风洞）或外场试验三种途径。传统直升机空气动力学领域中，结合数值计算的涡流模型应用最为广泛。涡流模型的实现需要借助计算机，和旋翼气动模型、数值算法一起，形成了浩瀚的模型变种和组合［7］。可用于流场计算的模型众多，已编写成代码模块应用较广的，至少包括OVERFLOW模型［8］，AGDISP实际使用并扩展到多旋翼的CHARM模型［9， 10］，以及黏性涡粒子或涡元法［11， 12］。然而上述代码或软件并不完全对外公开，自行编写工作量大，且同样涉及数值精度，计算量和稳定性问题，平均相对误差超过20%［13］。传统航空领域另有采用CFD或实验方法研究旋翼流场的极多工作，可为农业航空风场研究提供借鉴。

当前，农业航空领域对旋翼流场的研究尚处于起步阶段［14］。例如，AGDISP/AgDrift模型的公开论文［15， 16］处理直升机流场就存在理想化问题。该模型将直升机部分地看成固定翼飞机，认为桨盘下的流场初始为下洗流但迅速转换为翼尖涡主导，桨叶诱导的下洗流仅在旋翼下方，尖涡诱导的速度场随距离平方衰减。该流场模型只有当前飛速度较高才成立，而我国喷雾作业往往不符合条件。国外研究单旋翼直升机喷雾的文献也较少，从理论［17］和ANSYS Fluent［18］方面考虑了飞行速度和侧风对流场影响。国内农业航空界近年出于植保施药飘移预测的实际需求，使用数值模拟、实验室或田间试验方法研究直升机旋翼流场。田间法［5， 19］使用传感器研究无人机辅助授粉时，测量发现单旋翼风场流速沿飞行方向最大，垂直地面方向最小，随着飞机总重增加，航高降低，风速峰值逐步增大。实验室法［20， 21］使用不同测速技术捕捉到直升机不同悬停高度和前飞下洗流特征。CFD软件仿真［2228］观察到下洗流场主要集中在桨盘下方，伴有周向旋转和径向收缩运动。未计入地面效应情况下，下洗流最大值位于旋翼0.8R下方，随高度降低逐渐减小，风场宽度增大。如有机身阻挡［29， 30］，速度轴向分量比径向大，沿翼展方向先增加后减小［31］，在桨尖附近达最大值。除CFD软件外，另有应用格子玻尔兹曼机［3234］数值方法模拟单旋翼全机身，发现飞行速度与尾涡的关系，及对雾滴飘移的影响。

上述农业航空领域流场研究针对的均为特定机型和特定飞行状态，定性结果居多，不易推广扩展。试验手段成本太高，耗费人力物力，不易获得完整流场数据。CFD可以计算任意空间点速度，但只针对具体场景和应用，难以二次开发，且计算量大，使用普通计算机需耗费数小时乃至数十小时。因此保证合理精度，提出一种简单且相对有效方法用于旋翼流场速度计算具有实际意义。

涡环模型是一种消耗较少计算资源的方法，近年已引起一些学者关注，并成功应用于风力机气动建模［35］。由于风力机与直升机桨叶的相似性，本文选择涡环作为直升机旋翼尾流模型，研究旋翼周围空间流场的定量完整快速计算。忽略机身、尾翼等影响，将旋翼等效为作用盘，所发出尾迹用叠加的涡环代替，综合固定尾迹法或预定尾迹法确定涡环空间位置和半径，从而可利用Biot-Savart法则解析或半解析快速求出悬停和不同前飞速度下旋翼周围流场诱导速度及其特征。

1 理论和计算方法

1.1 涡环模型

涡流理论考虑旋翼尾流中涡量的分布，可以完整计算诱导流场。通常涡量分布在螺旋涡面上，即使采用最简单的固定尾迹法，从螺旋涡面计算诱导速度仍较复杂。注意到桨盘转速很快，每一圈拖出的涡面近乎圆形，而桨尖集中了桨叶的大部分涡量，故可用连续的涡环等效螺旋涡面。涡环是涡量高度集中在环状结构里的一种流体对象。以涡环中心为原点，建立圆柱坐标系（r，θ，z），则涡量空间分布

ω=Γδ（r－R）δ（z）

涡量位于圆心z=0、旋翼半径R的圆上，环量Γ固定。该涡环诱导出轴向速度w和径向速度u，均有解析表达式［35］。对圆柱坐标系下半径r、轴向z处的点，诱速为

u（r，z）=Γk4πRzRRr3/2－K（k）+2－k22（1－k2）E（k）（1）

w（r，z）=Γk4πRRr1/2K（k）+R2rk21－k2－2－k22（1－k2）E（k）（2）

k=2Rrz2+（R+r）2

式中：K（k）、E（k）——第一类和第二类完全椭圆积分。

1.2 滑流边界计算

涡环位置和直径由滑流（slipstream）边界确定。滑流边界与流场计算、喷头布置密切关联，边界内外的分割标志是桨尖涡。Landgrebe提出预定尾迹法，为确定尖涡位置和滑流边界，做了很多试验，得到定量结果［6］。依Landgrebe公式，画出悬停滑流边界如图1（a）所示，接近桨盘0.78R处，边界明显向内收缩，该现象不依赖桨叶具体几何结构，主要与桨叶雷诺数有关。

前飞时自由来流以与直升机航速V∞相同的值进入桨盘平面，滑流向飞机尾部斜下拖出，不再是悬停时的竖直状态。Beddoes通过确定入流分布估计桨尖涡竖向位置，依其计算可得到前进比μ=0.022时滑流边界示意图1（b）所示。

1.3 旋翼流场计算

按照固定尾迹法和涡环模型，桨叶旋转尖端不断发射出一圈圈涡环。如果桨盘由无穷多的桨叶构成（作用盘假设），那么涡环将连续组成圆柱涡面。传统固定尾迹法的尾迹结构除圆柱涡面外，还包括旋翼平面的涡盘（bound vortex disk）和沿转轴的根涡（root vortex）。涡盘和根涡激起周向速度分量。已知诱导流场以轴向速度为主，同时伴有周向和径向速度分量。一般计算时，径向速度可直接忽略，周向速度（切向或旋流速度）也很小，不到诱导功率的1%。故基于涡环模型计算诱导流场，实际中周向和径向速度的影响可忽略不计。

1.3.1 悬停状态

根据固定尾迹法单旋翼直升机悬停时涡环分布和坐标系如图2所示。

设前进方为x轴，沿径向y轴，z轴竖直向上，原点位于桨盘中心。设环量为Γ，圆柱坐标系切向单位分量eΨ，径向er，轴向ez，圆柱涡面的轴向分布区间为［0，z0］。由Biot-Savart法则，圆柱涡面诱导速度［35］为

u（r，z）=ΓR4π∫z00∫2π0eΨ（θ′）［r2+R2－2rRcos（θ′－Ψ）+（z－z′）2］1/2dθ′dz′（3）

设ζ=z-z′，计算得径向速度和轴向速度为

u（r，z）=ΓR2πr2－k2kK（k2）－2kE（k2）ζ2ζ1（4）

w（r，ζ）=－Γ4πRrζkK（k2）+R－rR+rΠ（k20，k2）ζ2ζ1（5）

其中ζ1=z，ζ2=z-z0，Π为第三类完全椭圆积分。令z0→∞，可解析求得旋翼稳定悬停后的径向和轴向诱导速度，实际计算中z0只需取较大数。

1.3.2 前飞状态

前飞时，旋翼尾迹呈一斜圆柱体（skewed cylinder），速度越快，倾斜越大。设圆柱倾角χ，桨盘迎角i，前飞尾流见图3。在图3中定义新坐标系x-ζ，ζ与原坐标变量x-z存在确定函数关系，设为ζ=f（x，z）。

在x-ζ坐标系中诱导速度公式与x-z坐标系下的圆柱涡面相同。函数f与尾流倾角χ相关，而倾角由式（6）确定。

tanχ=V∞cosiV∞sini+vi（6）

桨盘处诱导速度vi由式（7）给出。

vi=V∞sini+T2ρAvi2+（V∞cosi）2（7）

如果桨盘迎角i≈0，解得诱导速度为

vi=－V∞22+V∞222+vh4（8）

式中：vh——悬停时桨盘处诱速；ρ——空气密度；A——桨盘面积；T——拉力。vh=T/2ρA（9）

求出倾角χ后，涡环便可以按图3确定圆心空间位置，半径不变。由式（1）、式（2）求解单个涡环诱导速度，再将各涡环诱速叠加，最后的合速度就是斜圆柱尾流对空间点的诱导速度。尾流倾角χ与前进比（μ=V∞cosi/ΩR）相关，当μ≥0.15时，式（6）已不准确，旋翼尾流应作平面涡系处理［6］。如果对象是重型直升机，高速前飞下的旋翼则可以看成圆形固定机翼，尾流涡量集中在桨尖涡里，旋翼平面涡系可用桨尖涡对替代。AGDISP/AgDrift便如此处理，原因是美国施药所使用的多为大型直升机，且前飞速度快。

1.3.3 基于预定尾迹的旋翼流场

上两小节流场计算基于固定尾迹，假设尾流中涡环半径不变，这不符合事实。根据预定尾迹法确定的滑流边界就是涡环的分布界限。由该界限可确定各xy截面上涡环半径和圆心，继而计算诱导流场。如果用涡环模型表示悬停或前飞时的尾流，旋翼滑流边界在桨盘平面下的形态如图1所示。设左右两条边界曲线为z=f1，z=f2，则涡环中心为［f-11（z）+f-12（z）］/2，半径为|f－11（z）－f－12（z）|/2。同前飞斜圆柱情形一样，基于预定尾迹的旋翼尾涡是不规则圆柱，没有解析公式，可以利用单个涡环诱速式（1）、式（2）叠加计算，此为半解析法。

2 计算结果和分析

2.1 CFD仿真

目前以Ansys Fluent为代表的商业软件很成熟，农业航空领域也有较多直升机流场仿真成功案例。为定量验证涡环模型准确性，本文同时设计CFD仿真试验。首先使用ICEM CFD建立旋翼三维模型，略去机身、尾桨等结构。旋翼半径0.219 m，弦长0.032 m，转速2 400 r/min，桨叶扭转角-6°，桨叶尖线速度55.013 m/s。旋翼直径记为D。流域设置为无滑移圆柱体壁面，半径10D，上表面为速度入口，距旋翼10D，下表面为压力出口，距旋翼40D，如图4所示。借鉴张宋超等［29］方法设置动域和静域，动域为包含旋翼的较小空间，内部使用MRF动网格模型模拟桨叶旋转。静域和动域间使用interface连接传递计算，动域网格划分较细，无需生成边界层网格，经试验几乎对精度无影响，静域较粗。采用非结构化网格，总网格数量约150万。试验发现，网格数在120万～200万之间，仿真流场、压力云图等均无显著变化，且能捕捉到桨尖涡。故选择了偏小的网格数量，减少计算复杂度。使用Ansys Fluent仿真，检测网格质量后选择稳态，无压缩（桨尖马赫数Ma<0.3），基于压力的求解器，湍流方程为k-ω sst模型。梯度项计算为基于单元体的最小二乘法插值，压力—速度耦合采用二阶迎风格式的SIMPLE算法。设置自由来流0 m/s，模拟悬停状态。当残差至少下降三个数量级以上才认为计算收敛。仿真完成后使用后处理软件Tecplot打开数据文件，导出流场相应数据，方便与模型计算结果比较。

2.2 悬停流场

悬停状态下的流场可根据式（4）、式（5）计算。流场速度理论上可以解析求出，但式（4）、式（5）中的椭圆积分无法手动计算，且实际积分限并非无穷，故需使用计算机。此处应用的是普通PC机，配置为Intel CPU T6400 2 GHz，內存2 GB，计算软件MATLAB，用时2.8 s，是一种半解析方法。

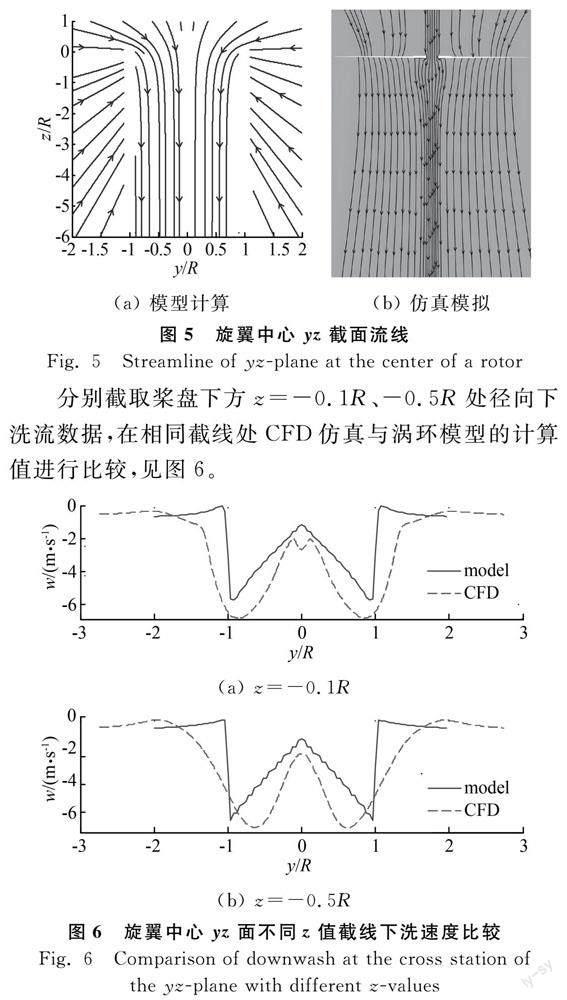
因圆柱涡面对称性，取yz截面研究，悬停时模型计算和CFD仿真的旋翼流场流线见图5。模型计算的尾流内部流场称为下洗流，之外为上洗。尾流内流线与CFD整体相同，均竖直向下，且有收缩。不同的是由于能量耗散，CFD下洗流场先收缩后扩大，相应速度则先增加后减少，符合张宋超等［30］研究的结论。涡环模型没有考虑涡量耗散，流场宽度只在桨盘处（z=0）收缩，没有明显扩充变化。因为桨盘旋转带来的压差，上方旋翼周围空气被吸入桨盘，但并不流经桨盘面覆盖的整个下方空间，传统结果是气流半径突然收缩为0.78R。CFD流场在桨盘处收缩体现得较为剧烈，而观察模型流线图坐标，收缩半径大约为0.9R，相对误差15.4%。考虑到涡环模型较简单，该精度已能令人满意。

分别截取桨盘下方z=-0.1R、-0.5R处径向下洗流数据，在相同截线处CFD仿真与涡环模型的计算值进行比较，见图6。

模型计算的流场速度范围为-7.2～0.3 m/s，而CFD仿真的诱速范围为-7.5～0.2 m/s，根据式（8）计算的桨盘诱导速度为-6.9 m/s。模型和CFD两者曲线的总趋势是从中心开始沿径向递增至桨尖附近最大，越过滑流边界受桨尖涡影响迅速转为上洗，而后诱导速度减弱趋于0。故尾流圆柱以外，即上洗流区域和桨盘平面上方气流速度很小，在直升机空气动力学中常被视作静流区。在同一高度，尾流内部平均下洗速度是外部最大上洗速度的5倍以上。从曲线看CFD仿真的下洗速度值和收缩程度均比模型大，在y=0.8左右达最值（模型y=0.9处最大），与图5滑流边界一致，而上洗流表现不如模型剧烈，显示CFD流场捕捉的空间分辨率不够。原因很可能是使用MATLAB逼近CFD数据时步长偏大，错过了桨尖涡效应。此外因为无机身遮挡，与刘鑫［20］和张宋超［30］报道的中心诱速近于0不同，本算例模型预测桨盘下z=-0.1R中心点有较小下洗流w≈-0.5 m/s，为平均下洗流值（-3 m/s）的16.67%。CFD曲线上桨盘中心速度值为平均速度的42.83%。在转轴下方z=-0.5R处CFD曲线原点的峰值消失，可能是根涡诱导效应减弱所致。涡环模型不考虑根涡，故原点周围速度无波动。

在yz平面离中心y=0.1R、0.5R、0.9R处，下洗流沿轴向分布如图7所示。

CFD仿真和模型计算均表明桨盘旋翼上方为下洗流。CFD曲线离旋翼平面越近速度值越大，中心附近区域上方有一峰值，此后接近旋翼速度递减。CFD径向不同位置的三条曲线均在桨盘平面处表现出振荡行为。越过桨盘平面后y=0.1R、0.5R处CFD曲线模拟的下洗速度先增大后减小。y=0.9R处受桨尖涡影响，轴向的平均下洗数值较大，无明显能量耗散。涡环模型因为比较简单，仅曲线y=0.1R下洗流在桨盘上方波动，其余曲线速度值均沿轴向一路递增。跨越桨盘时模型与CFD曲线行为相差较大，其他位置绝对速度误差最大约3 m/s，相对误差为42%。说明考虑能量耗散对预测速度轴向分布很重要，模型与CFD吻合度需要进一步提高。

Landgrebe由多个模型计算和试验测量得到下洗流径向分布［6］，可以定性表述为：除桨叶尖端外，0.2R～0.9R范围流速近似保持线性递增。与图6基本吻合，说明本算例的仿真和计算是可靠的。

2.3 前飞流场

下面考虑前飞情形。前飞旋翼尾流非定常，随桨叶方位角变化大，CFD瞬态仿真需较强算力，故这里与前人的标准结果对照。NASA的Heyson［36， 37］对独立旋翼流场做了大量测算工作，发布了一系列可靠报告，为下面算例比较参照。

现设尾流倾角χ为45°，绘制诱导流场xz截面流线如图8所示。圆柱中的尾流斜向下运动，而圆柱下方滑流边界外的气流包含较小的下洗分量，气流主要向前方上卷，离旋翼桨盘边沿越近，对应坐标（1，0）处，上卷越强烈。注意到图中流线从上到下穿透尾流，实际中是不存在的。出现该现象一则因MATLAB数值计算误差，二因未捕捉到桨尖涡，而桨尖涡是滑流内外分界的标志。

随着前飞速度加大，斜圆柱形态的尾流倾角将增大，其边界下方上洗流区域缩小，逐渐前移到飞行前方，原来区域转为下洗流。最极端情况尾流水平向后拖出，旋翼下方诱导速度完全下洗，仅水平前方上洗。我国中小型农用直升机通常前飞速度较小，以农业农村部南京农业机械化研究所N-3直升机为例［29］，平飞速度V∞=3 m/s，旋翼转速Ω=828 r/min，桨盘直径D=3.115 m，则前进比μ=0.022，尾流倾角χ=22°，远达不到水平尾流状态。

从图8可以看出，飞行方向旋翼前后流场不对称。令z=-0.2R，得到沿x轴分布的下洗速度，并与Heyson［36］结果比较，如图9所示，纵坐标已使用平均诱导速度v0无维化。Heyson给出的是无维化后的数据，并未给定v0，故需要模型同时无维化与之比较速度分布形态。桨盘后缘曲线值显著高于前缘，桨盘范围以外后方为下洗，前方上洗，2R外趋于0。桨盘后缘最大诱速为平均值v0的1.4～1.8倍，前缘处为平均值0.2～0.5倍。x=±R处速度有一个跳变，进入桨盘前缘从上洗转为下洗，脱离桨盘后缘下洗值急剧减小。略有不同的是，Heyson曲线很准确地定位跳变点在x=±R，而模型曲线向后方有约0.2R平移，且行为模式更复杂，表现为先增大后减少。这是桨尖涡临近速度的典型行为，Heyson因试验测量，传感器布置不够密，空间分辨率欠缺，有可能错过流场的精细行为。此外，模型预测的滑流边界外诱导速度比Heyson试验值偏小。

植保施药时，喷头通常安装在旋翼后下方。该位置的速度特征直接关系到喷头布置。设典型参数χ=75°，x=0.5R，取旋翼上下两条截线z=0.3R，z=-0.12R，绘制下洗流沿y轴分布曲线，和Heyson［37］结果见图10。

旋翼上方z=0.3R处模型和试验结果吻合得非常好，下洗流几乎在整个桨面上维持稳定。旋翼下方z=-0.12R处超出尾流区域时上洗流较大，但在中心y=0处两种方法差异明显。模型预测为下洗流，Heyson试验测量曲线则轻微上洗。由计算结果可知，z=-0.12R处已接近尾流边界，容易受桨尖涡影响，加之前飞尾流复杂，致使此处模型不太准确。而在0.5R～0.8R区域，模型與试验一致，此区域也是布置喷头，最大限度利用下洗流场的地方。故x=0处误差并不影响实际喷头处模型速度估计。

2.4 误差分析

对悬停情形，以CFD曲线为基准，根据图6、图7计算模型与CFD间的误差Δw，并取绝对值|Δw|。由对称性，径向只取正半轴，绘制误差曲线如图11所示。对y轴范围-R～R，z轴下方0～4R计算各项误差指标（最大误差、平均误差、平均相对误差），并设线性回归函数y=p1x+p2，拟合模型和CFD值，得到表1。

综合表1和图11，径向上下洗流转换位置y=1.1R～1.2R处误差最大，为6.6 m/s，原因可能为桨尖涡位置模型预测值与CFD并非完全一致，模型预测为上洗流时CFD还是下洗。轴向桨盘z=0处和洗流耗散将要衰减处（y=2R），误差最大分别达到7.8 m/s和4.2 m/s。除个别极端点外，模型与CFD间径向平均误差小于1.71 m/s，平均相对误差小于39.1%，轴向平均误差小于2.26 m/s，平均相对误差小于54.6%。除軸向y=0.5R外，模型与CFD线性拟合决定系数R2均大于0.72，均方根误差RMSE小于0.52，说明模型可以经简单线性回归矫正达到同CFD仿真接近的效果。值得注意的是y=0.5R和y=0.9R的拟合系数p1小于0，说明模型与CFD数据负相关，原因是CFD曲线先增后减，而模型曲线是严格的增函数，导致远离桨盘时诱速趋势不一致。

对前飞情形，以Heyson曲线为基准，根据图9、图10计算模型与Heyson曲线间的误差，并取绝对值设为E，如图12所示。同样计算各项误差并线性拟合得到表2。

由于Heyson试验数据已经做无维化处理，且无法获知该因子v0，故无法得到真实速度误差。无维化的意义是为不同参数的试验或计算提供统一比较。对χ=45°，z=-0.2R，平均误差0.2，最大误差在滑流边界x=±R。对χ=75°，z=-0.12R、z=0.3R，平均误差小于0.71，中心和边界处误差最大。三条曲线的决定系数均大于0.73，最大为0.8，表明模型与试验数据相关性较强。

实际尾流圆柱内部充满涡量，且涡环半径比理论值小，而涡环模型假定涡量自桨尖发出构成圆柱面，这是速度误差的根源。模型计算值比实际小，但速度曲线形态一致，并有较强线性相关性，这就可以改进涡环模型，精细地向圆柱内补充涡量，或通过线性回归调整模型数据，减小速度误差。

3 讨论

涡环模型能够定量计算一般旋翼流场，不局限具体直升机型号，还可以定性分析速度规律，合理化喷头布置。

设无维化系数w0=Γ/2πR，由式（1）、式（2）知实际速度依赖此系数，不同旋翼或直升机w0数值并不相同。对涡环模型而言，流场形态、径向或轴向速度相对于平均速度的比例，不同直升机均为一致，只是绝对数值在变，需要乘以系数w0获得真实速度。悬停情形［6］，有

w0=W/NπρΩR3

这样飞机总重W、桨片数量N、空气密度ρ、旋翼转速Ω、旋翼半径R等直升机具体参数均包含在无维化系数w0或环量Γ中，各参数影响最终通过w0体现。w0越大实际速度越大。一般农用单旋翼桨叶数N=2，故速度是总重W的增函数，是空气密度ρ，转速Ω，旋翼半径R的减函数。不同作业环境下，空气密度ρ变化较大，海平面与高原可相差30%～40%，诱速改变近30%，所以直升机高原作业时下洗速度变大。拉力T常与桨尖速平方成比例，T∝v2tip=（ΩR）2。即是说给定某直升机总重W（等于T）和旋翼半径R，旋翼转速Ω是W和R的因变量，并不能随意变化。这正是一些轻型单旋翼直升机转速高的原因，其桨盘直径小，维持相同载荷必须通过高转速弥补拉力。故悬停状态流场主要受W、ρ、R的影响。又知R微小变化导致无维化系数w0与其三次方成反比，而同一区域地表空气密度ρ变化不大，因此流场影响因素重要性排序为R、W、ρ。

前飞情况较复杂，可以认为［6］

w0=1－1.5μsinΨ1－1.5μ2WNπρΩR3cosi=FG

式子中包含F和G两项。桨盘迎角i≈0，第二项与悬停相同。绘制第一项函数

F=1－1.5μsinΨ1－1.5μ2

关于前进比μ和方位角Ψ的云图如图13所示。可以看出，当方位角Ψ运行在三、四象限时比一、二象限诱导的流场速度大。μ增大，前行桨叶（一、二象限）诱速减小，后行桨叶（三、四象限）诱速增大。实际农用单旋翼直升机喷雾不可能考虑前后行桨叶情况，只能计及平均效应。根据式（7）诱速是航速的减函数。故前飞状态流场主要受W、ρ、R、V∞的影响。由于前飞速度可控性最强，变化最灵活，按重要性前飞流场影响因素依次为V∞、R、W、ρ。这里仅从涡环模型予以理论分析，实际流场还很复杂，与桨叶几何、飞行高度、作业环境等诸多因素相关。

当选定农用单旋翼直升机和作业环境后，流场便主要与V∞相关。前飞速度越小，流场越接近悬停状态。悬停或接近悬停时滑流内部气流速度大，施药效果好，但工作效率降低。所以应根据实际作业要求选择合适前飞速度，在工作效率和施药质量间达到平衡。

已知滑流外部为上洗流或微弱的下洗流，雾滴需要较长时间沉降，且受自然风影响，容易偏离靶标。那么应该根据尾流倾角χ调整喷头位置和角度，使释出雾滴落入滑流内部。目前单旋翼施药时，相当部分喷杆沿y轴横向布置在旋翼中央正下方。当增加前飞速度，滑流偏离中心，向后倾斜较大时，所有喷头将裸露在滑流界外，无法利用下洗气流，易于飘失。如果将喷头向桨盘后缘移动，或喷杆纵向沿x轴放置，则可以利用后缘更大下洗流，提高施药质量，减少飘失农药带来的环境污染。

4 结论

1） 本文针对目前农业航空领域流场研究成本高、耗时耗力状况，提出一种基于半解析涡环模型用于旋翼流场速度计算。该模型简单快速，在普通PC机（CPU 2 GHz，内存2 GB）上可2.8 s完成计算。模型与CFD仿真和试验数据趋势一致。

2） 悬停时径向平均误差小于1.9 m/s，平均相对误差小于39.1%，轴向平均误差小于2.26 m/s，平均相对误差小于54.6%，除y=0.5R轴向截线外，其他模型数据与基准曲线间的线性拟合决定系数R2均大于0.72，最大为0.934 8。前飞时模型与试验曲线的决定系数均大于0.73，最大为0.803 3。悬停时桨盘及下方0.5R区域内，中央下洗流较小，沿径向速度增加，越过尾流区域后表现为上洗，迅速衰减。前飞时，桨盘后缘比前缘速度大。当前飞速度增大，滑流外速度方向由上洗逐渐水平呈卷扬气流甚至变成下洗。

3） 旋翼流场主要影响因素依次是前飞速度、旋翼半径、飞机总重、空气密度。通常诱导流场速度随飞机总重增加而变大，随旋翼半径、空气密度、前飞速度增加而变小。

参 考 文 献

［1］姚伟祥， 兰玉彬， 王娟， 等. AS350B3e直升机航空喷施雾滴飘移分布特性［J］. 农业工程学报， 2017， 33（22）： 75-83.Yao Weixiang， Lan Yubin， Wang Juan， et al. Droplet drift characteristics of aerial spraying of AS350B3e helicopter ［J］. Transactions of the Chinese Society of Agricultural Engineering， 2017， 33（22）： 75-83.

［2］王昌陵， 何雄奎， 曾爱军， 等. 基于仿真果园试验台的植保无人机施药雾滴飘移测试方法与试验［J］. 农业工程学报， 2020， 36（13）： 56-66.Wang Changling， He Xiongkui， Zeng Aijun， et al. Measuring method and experiment on spray drift of chemicals applied by UAV sprayer based on an artificial orchard test bench ［J］. Transactions of the Chinese Society of Agricultural Engineering， 2020， 36（13）： 56-66.

［3］Li J， Shi Y， Lan Y， et al. Vertical distribution and vortex structure of rotor wind field under the influence of rice canopy ［J］. Computers and Electronics in Agriculture， 2019， 159： 140-146.

［4］李继宇， 周志艳， 胡炼， 等. 单旋翼电动无人直升机辅助授粉作业参数优选［J］. 农业工程学报， 2014， 30（10）： 10-17.Li Jiyu， Zhou Zhiyan， Hu Lian， et al. Optimization of operation parameters for supplementary pollination in hybrid rice breeding using uniaxial single-rotor electric unmanned helicopter ［J］. Transactions of the Chinese Society of Agricultural Engineering， 2014， 30（10）： 10-17.

［5］招启军， 徐国华. 直升机计算流体动力学基础［M］. 北京： 科学出版社， 2016.

［6］Johnson W. Helicopter theory ［M］. Courier Corporation， 2012.

［7］Komerath N M， Smith M J， Tung C. A review of rotor wake physics and modeling ［J］. Journal of the American Helicopter Society， 2011， 56（2）： 22006.

［8］Yoon S， Pulliam T H， Chaderjian N M. Simulations of XV-15 rotor flows in hover using overflow ［J］. Proceedings of the 50th AHS Aeromechanics Specialists， AHS， San Francisco， CA， 2014： 1-11.

［9］Wachspress D A， Quackenbush T R， Boschitsch A H. Rotorcraft interactional aerodynamics with fast vortex/fast panel methods ［J］. Journal of the American Helicopter Society， 2000， 48（4）： 223-235.

［10］Teske M E， Wachspress D A， Thistle H W. Prediction of aerial spray release from UAVs ［J］. Transactions of the ASABE， 2018， 61（3）： 909-918.

［11］He C， Zhao J. Modeling rotor wake dynamics with viscous vortex particle method ［J］. AIAA Journal， 2009， 47（4）： 902-915.

［12］魏鵬， 史勇杰， 徐国华， 等. 基于黏性涡模型的旋翼流场数值方法［J］. 航空学报， 2012， 33（5）： 771-780.Wei Peng， Shi Yongjie， Xu Guohua， et al. Numerical method for simulation rotor flow field based upon viscous vortex model ［J］. Acta Aeronautica  et Astronautica Sinica， 2012， 33（5）： 771-780.

［13］Chen R， Yuan Y， Thomson D. A review of mathematical modelling techniques for advanced rotorcraft configurations ［J］. Progress in Aerospace Sciences， 2021， 120： 100681.

［14］田志伟， 薛新宇， 李林， 等. 植保无人机施药技术研究现状与展望［J］. 中国农机化学报， 2019， 40（1）： 37-45.Tian Zhiwei， Xue Xinyu， Li Lin， et al. Research status and prospects of spraying technology of plant-protection unmanned aerial vehicle ［J］. Journal of Chinese Agricultural Mechanization， 2019， 40（1）： 37-45.

［15］Bilanin A J， Teske M E， Barry J W， et al. AGDISP： The aircraft spray dispersion model， code development and experimental validation ［J］. Transactions of the ASAE， 1989， 32（1）： 327-334.

［16］Teske M E， Bird S L， Esterly D M， et al. AgDRIFT （R）： A model for estimating near-field spray drift from aerial applications ［J］. Environmental Toxicology and Chemistry， 2002， 21（3）： 659-671.

［17］Parkin C S. Rotor induced air movements and their effects on droplet dispersal ［J］. The Aeronautical Journal， 1979， 83（821）： 183-187.

［18］Seredyn T P. A computational study of the fluid particles distribution in an helicopter wake ［C］. Journal of Physics： Conference Series. IOP Publishing， 2018， 1101（1）： 012032.

［19］汪沛， 胡炼， 周志艳， 等. 无人油动力直升机用于水稻制种辅助授粉的田间风场测量［J］. 农业工程学报， 2013， 29（3）： 54-61， 294.Wang Pei， Hu Lian， Zhou Zhiyan， et al. Wind field measurement for supplementary pollination in hybrid rice breeding using unmanned gasoline engine single-rotor helicopter ［J］. Transactions of the Chinese Society of Agricultural Engineering， 2013， 29（3）： 54-61.

［20］刘鑫. 单旋翼植保无人机旋翼流场下洗气流速度分布规律研究［D］. 大庆： 黑龙江八一农垦大学， 2019.Liu Xin. Research on distribution regularity of downwash airflow velocity in rotor flow field of single rotor plant protection UAV ［D］. Daqing： Heilongjiang Bayi Agricultural University， 2019.

［21］Tang Q， Zhang R， Chen L， et al.High-accuracy， high-resolution downwash flow field measurements of an unmanned helicopter for precision agriculture ［J］. Computers and Electronics in Agriculture， 2020， 173： 105390.

［22］石強， 管贤平， 孙宏伟. 基于CFD的小型植保无人直升机喷雾场数值模拟［J］. 江苏农业科学， 2016， 44（9）： 360-364.Shi Qiang， Guan Xianping， Sun Hongwei. Numerical simulation of spray field of small unmanned helicopter for plant protection based on CFD ［J］. Jiangsu Agricultural Sciences， 2016， 44（9）： 360-364.

［23］石强. 小型无人直升机超低空飞行时下洗流场数值分析［J］. 排灌机械工程学报， 2015， 33（6）： 521-525.Shi Qiang. Numerical simulation for downwash flow field of small-size unmanned helicopter hedgehopping ［J］. Journal of Drainage and Irrigation Machinery Engineering， 2015， 33（6）： 521-525.

［24］王军锋， 徐文彬， 闻建龙， 等. 大载荷植保无人直升机喷雾气液两相流动数值模拟［J］. 农业机械学报， 2017， 48（9）： 62-69.Wang Junfeng， Xu Wenbin， Wen Jianlong， et al. Numerical simulation on gas-liquid phase flow of large-scale plant protection unmanned aerial vehicle spraying ［J］. Journal of Agricultural Machinery， 2017， 48（9）： 62-69.

［25］徐文彬， 王军锋， 闻建龙， 等. 大载荷植保无人直升机近地飞行流场模拟［J］. 江苏大学学报（自然科学版）， 2017， 38（6）： 665-671.Xu Weibin， Wang Junfeng， Wen Jianlong， et al. Numerical simulation for downwash flow field of large-size plant protection unmanned helicopter hedgehopping ［J］. Journal of Jiangsu University （Natural Science Editions）， 2017， 38（6）： 665-671.

［26］杨知伦， 葛鲁振， 祁力钧， 等. 植保无人机旋翼下洗气流对喷幅的影响研究［J］. 农业机械学报， 2018， 49（1）： 116-122.Yang Zhilun， Ge Luzhen， Qi Lijun， et al. Influence of UAV rotor down-wash airflow on spray width ［J］. Transactions of the Chinese Society for Agricultural Machinery， 2018， 49（1）： 116-122.

［27］贾志成. 小型无人直升机航空喷雾试验系统及喷雾流场研究［D］. 南京： 南京林业大学， 2018.Jia Zhicheng. Research on aerial spray testing system and spraying flow field for small unmanned aerial vehicle ［D］. Nanjing： Nanjing Forestry University， 2018.

［28］边永亮， 李建平， 王鹏飞， 等. 单旋翼无人机流场分布特征及作业性能试验研究［J］. 河北农业大学学报， 2020， 43（3）： 115-120， 129.Bian Yongliang， Li Jianping， Wang Pengfei， et al. Experimental study on distribution characteristics and operating performance of airflow field in single rotor UAV ［J］. Journal of Hebei Agricultural University， 2020， 43（3）： 115-120， 129.

［29］张宋超， 薛新宇， 秦维彩， 等. N-3型农用无人直升机航空施药飘移模拟与试验［J］. 农业工程学报， 2015， 31（3）： 87-93.Zhang Songchao， Xue Xinyu， Qin Weicai， et al. Simulation and experimental verification of aerial spraying drift on N-3 unmanned spraying helicopter ［J］. Transactions of the Chinese Society of Agricultural Engineering， 2015， 31（3）： 87-93.

［30］张宋超， 薛新宇， 孙竹， 等. 单旋翼油动无人施药直升机悬停状态下风场下洗气流分布规律研究［J］. 中国农业文摘-农业工程， 2018， 30（3）： 13-22.

［31］王军. 单旋翼非定常流场的数值模拟及尺度效应的研究［D］. 杭州： 浙江大学， 2018.Wang Jun. Numerical study of the unsteady flow field of a single rotor and the scale effect ［D］. Hangzhou： Zhejiang University， 2018.

［32］文晟， 韩杰， 兰玉彬， 等. 单旋翼植保无人机翼尖涡流对雾滴飘移的影响［J］. 农业机械学报， 2018， 49（8）： 127-137， 160.Wen Sheng， Han Jie， Lan Yubin， et al. Influence of wing tip vortex on drift of single rotor plant protection unmanned aerial vehicle ［J］. Transactions of the Chinese Society for Agricultural Machinery， 2018， 49（8）： 127-137， 160.

［33］Tang Q， Zhang R， Chen L， et al. Numerical simulation of the downwash flow field and droplet movement from an unmanned helicopter for crop spraying ［J］. Computers and Electronics in Agriculture， 2020， 174： 105468.

［34］Tang Q， Chen L， Zhang R， et al. Effects of application height and crosswind on the crop spraying performance of unmanned helicopters ［J］. Computers and Electronics in Agriculture， 2021， 181： 105961.

［35］Branlard E. Wind turbine aerodynamics and vorticity-based methods： Fundamentals and recent applications ［M］. Springer， 2017.

［36］ Jewel J W J， Heyson H H. Charts of the induced velocities near a lifting rotor ［R］. NASA-MEMO-4-15-59L， 1959.

［37］Heyson H， Katzoff S. Induced velocities near a lifting rotor with nonuniform disk loading ［R］. NACA-TR-1319， 1957.

基金项目：国家重点研发计划项目（2017YFD0701000）

第一作者：金濟，男，1980年生，湖北荆门人，博士，讲师；研究方向为植保施药雾滴飘移建模。E-mail： ji_king314@scau.edu.cn

通讯作者：薛新宇，女，1969年生，江苏苏州人，博士，研究员；研究方向为植保机械与施药工程。E-mail： 735178312@qq.com