基于前置探究 确定学习路径
——以“ 长方形和正方形的面积计算”教学为例
文/中山火炬高技术产业开发区第五小学 刘林源
前置性探究是根据教学的核心目标, 针对重点难点和关键问题,设计探究任务,引导学生在上课前进行自主探究、 主动摸索、积极建构知识。 那么,如何基于前置性探究,确定学生的学习路径? 本文以 “长方形和正方形的面积计算”教学为例,从精准分析教材与学情、前置探究任务设计、确定学习路径进行阐述。
一、精准分析教材与学情
基于前置性探究的学习需要,教师精准把握教材的知识结构,分析教学内容,把准教学重难点,以及充分了解学情和认知规律, 方能有效地设计前置探究单, 促进学生对知识的自主构建。
二、前置探究任务设计
前置性探究任务单的设计是有效实施前置探究的关键,其探究任务具有很强的导向性、 针对性,引导学自主探究经历知识的形成过程。 教师要结合学习的具体内容,根据学生的认知特点和认知规律,在教学的重点、难点处设计探究活动,引导学生自主探究,经历数学化过程,助推学生积累数学活动经验,提升主动思考、乐于探究的思维品质。
1.不同教材细化对比
不同版本教材编排, 其侧重点可能不同, 将各版本的教材进行分析对比,可帮助教师确立重难点,并可借鉴各版本的优点, 巧用适合素材。为此,笔者将人教版、北师大版、苏教版 “长方形和正方形面积的计算”这一内容的教材进行对比,梳理编排的相同点和不同点。
三个版本最大的相同点, 都是用面积单位去测量长方形的面积,突出面积的本质是度量的结果,再通过1 平方厘米的小正方形拼摆出不同的长方形, 学生在操作和观察中感悟长和每行个数、 宽和摆的行数, 以及面积单位个数和长方形面积的关系, 再抽象概括出长方形正方形的面积计算公式, 从而让学生理解面积计算的意义。
2.核心目标具体化
本节课的核心目标是“理解长方形正方形的面积计算的意义”,需要借助大量的操作活动,让学生在活动中去观察、感悟。 怎样才算是真正理解? 在前置探究活动中,怎样才能看到学生思维的发生发展过程? 这时,很有必要将目标细化、具体化、层级化。 结合彼格斯的solo 分类理论的五个层次, 将本节课的核心目标具体化,即根据学生对核心目标理解的具体表现进行思维水平的划分。 “长方形和正方形的面积计算”核心目标的具体表现如下。
核心目标: 理解长方形正方形面积计算的意义。
具体表现:(1)方形的周长和面积混淆不清;(2)只能用1 平方厘米的小正方形去度量长方形面积;(3)除了用面积单位度量, 还会用借用画图或只铺图形的部分等方式去探究长方形的面积;(4)能用面积单位度量,并理解长与每行摆的个数、宽与摆的行数, 面积单位个数与面积之间的联系;(5)能利用以上的学习经验迁移应用到推导长方体正方体的体积计算。
Solo 分类层次: 水平0, 前结构;水平1,单点结构;水平2,多点结构;水平3,关联结构;水平4,抽象拓展。
要使学生的前置探究作品,能反映学生不同的思维层次, 教师在设计前置探究任务时, 探究任务应是低门槛且又是开放的, 不仅所有学生都能参与, 而且学生有不同的想法都有所体现。这样,教师就可根据学生的探究作品分析其思维处于哪一层次, 为后续教学提供有效支撑。
3.明确探究任务
基于以上教材分析和目标具体化,结合学生的实际情况,精心设计的以下两个适度开放的探究任务,让学生通过摆一摆、 分一分、 数一数,算一算这一系列过程,帮助学生积累丰富的表象, 实现操作经验与思考经验、策略性经验的有机融合,引导学生在探究活动中体验, 亲历实践过程, 初步感悟面积大小是度量的本质。
前置探究任务1: 用浅色彩笔涂一涂图1、图2 两个图形的面积,再比较两个图形的面积大小。

图1

图2
设计意图: 考查学生会不会将周长和面积混淆, 对应的是具体目标的最底层次,另外,能否用面积单位去测量图形的面积。
前置探究任务2: 想办法求出下面4 个长方形(图3)的面积。 可以用1 平方厘米的小正方形摆一摆,也可以用铅笔、直尺分一分。
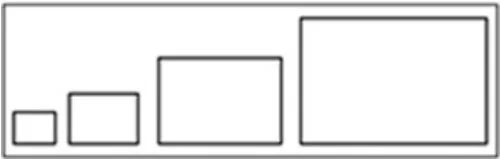
图3
设计意图:让学生在多次操作、拼摆的过程中,去感悟、观察长与每行摆的个数、宽与摆的行数、面积单位个数与面积之间的关系。
三、确定学习路径
长方形、 正方形面积大小的本质是度量, 公式只是便于操作化的形式。因此,在教学时需要充分利用学生的前置探究成果, 层层深入地选取有代表性的作品, 必要时在课堂上进行二次探究, 逐层经历由本质到形式的过程。基于前面的分析,确定这节课学生的学习路径。
环节一: 呈现前置探究1 题的正反两种探究成果,明晰面积概念,进一步区别周长与面积。
环节二: 巧用前置探究2 题的学生作品,有代表性、有层次地呈现,组织学生汇报交流、观察对比,教师适时的引导点拨,让学生初步理解长与每行摆的个数、 宽与摆的行数、面积单位个数与面积之间的联系。
环节三: 通过课堂上的二次探究,再次让学生动手操作,用面积是1 平方厘米的小正方形拼摆出不同的长方形。汇报的时候,先让学生看拼摆图形的想长方形的长、 宽与面积分别是几,然后看记录的数据,想象拼出长方形是怎样的。 这样把操作和想象内化相互结合, 进一步验证上述的关系, 概括出长方形的面积计算公式。
环节四:沟通长方形与正方形的联系,推导正方形的面积计算公式。
环节五:巩固练习,深化学生对面积本质的理解。
以上学习路径, 学生利用前置性探究任务,经历前置操作、思考与观察, 初步感知面积的大小是度量的本质。 教师在课堂上适时的引导点拨,深入进行二次探究,促进学生真正理解知识的本质。

