基于改进KCF算法的织物折皱回复检测研究
郭栩源 李忠健 王蕾 潘如如 高卫东


Research on fabric wrinkle recovery detection based on an improved KCF algorithm
摘要:织物折皱回复性能是评价织物形态稳定性的关键指标。传统折皱回复角测试方法存在检测过程依赖人工操作、难以量化折皱动态演变等问题。为实现对折皱回复全过程的自动化监测,文章提出一种基于改进核相关滤波算法的动态折皱回复检测方法。该方法使用高速摄像机捕捉织物折皱形变回复过程,应用改进的核相关滤波算法检测追踪折皱顶点的运动角度变化。通过引入多特征融合提高检测鲁棒性,利用Canny边缘检测自适应调整目标区域,减小边界效应。在此基础上提取感兴趣区域骨架,计算折皱顶角度随时间变化信息。结果表明,不同织物折皱角度变化规律与织物组织结构高度相关。最后与标准测试结果建立线性模型,验证所提方法的有效性。文章实现了对织物折皱回复全过程的自动化检测与定量评估,提供了一种更为高效准确的折皱回复性能检测新思路,具有广阔应用前景。
关键词:折皱回复角;特征融合;目标追踪;核相关滤波器;改进KCF
中图分类号:TS103.7
文献标志码:A
文章编号:10017003(2024)04007908
DOI:10.3969j.issn.1001-7003.2024.04.010
收稿日期:20230731;
修回日期:20240307
基金项目:纺织之光应用基础研究计划项目(J202109);国家自然科学基金项目(61802152);浙江省基础公益研究计划项目(LGG21F030007);中国博士后科学基金面上资助项目(2020M681736);江南大学研究生科研与实践创新项目(KYCX-23-ZD0 KYCX-23-ZD02)
作者简介:郭栩源(1997),男,硕士研究生,研究方向为数字化纺织技术。通信作者:王蕾,副研究员,wangl_jn@163.com。
织物折皱回复性能是评价织物形态稳定性的一项重要指标。在服装生产和日常使用过程中,织物都会出现不同程度的折皱,而折皱的快速消除对保证织物手感舒适、外观效果及提高生产效率都有重要影响,织物折皱回复性能的优劣在某种程度上直接决定面料及服装的品质与档次[1]。良好的折皱回复性能可以使织物在折叠、运输、加工等情况下迅速恢复原状,从而提高织物的实用性。
目前,国内外广泛采用的评价织物折皱回复性能的标准测试方法主要是折皱回复角测试,即对织物进行折叠加压处理,然后放松对其约束并在一定条件下测量其自然回复的折痕角度大小,以评估织物的折皱回复能力[2]。这种方法操作简便,能够直观反映织物的折皱回复程度。但是传统折皱回复角测试方法也存在一些问题,主要体现在:1)检测过程需要过多人工参与,效率较低[3];2)测试结果易受人为因素影响,难以保证测量时间的准确及角度测量的精度[4];3)无法区分不同时刻的折皱回复情况[5]。因此,这种方法只能给出折皱回复性能的整体略评,对织物折皱回复规律的细节描述不够。针对传统折皱回复角测试法的不足,学术界提出了一些改进方案,如在标准测试的基础上增加不同方向折皱回复角度检测[6]、结合图像处理技术计算折皱面积比例[7]等。这些方法扩展了测试指标,但仍然存在检测过程依赖人工操作、难以量化折皱动态演变等问题[8]。因此,开发一种能够实现对织物折皱回复全过程的自动化检测与分析方法,对于提高折皱回复性能的测试效率与结果可靠性具有重要意义[9]。
为实现对织物折皱的全自动检测分析,降低系统计算开销,提高分析针对性和精确度,本文将折皱顶点区域作为目标进行跟踪分析。在众多目标跟踪算法中,由于KCF(Kernel Correlation Filter)算法[10]具有极强的鲁棒性和实时性,在对运动目标追踪方面具有良好的表现效果[11],本文决定使用KCF算法作为织物折皱顶角跟踪算法。KCF算法是一种高效的核相关滤波算法,由Henriques等[10]在2012年提出,KCF算法属于由Bolme等[12]所提出的相关滤波器算法的一种,是在MOSSE(Minimum Output Sum of Square Error)算法基礎上引入高斯核、循环矩阵、脊回归等相关概念。新特性的引入同时带来了跟踪精度下降、边界效应等问题出现。针对这些问题,Bertinetto等[13]在KCF算法基础上加入颜色特征,但当目标发生形变时仍会丢失目标信息。潘长城等[14]提出融合类残差更新策略的KCF改进算法,但该算法在对目标进行持续跟踪时仍有部分时刻丢失目标信息,无法完整记录目标状态信息。孙晓锋等[15]使用目标丢失重检测及扩充区域重检测的方法,但很难对丢失目标进行重新定位。为了对织物折皱顶角进行完整准确跟踪,本文提出一种多特征融合及自适应边界调整的KCF算法。该算法能够对织物折皱顶角的整个动态过程进行完整跟踪检测,保证本文整套测试方法的有效性和准确性。
1 织物折皱回复性检测方法
1.1 方法概述
本文提出了一种基于改进KCF算法的织物折皱回复检测方法,流程如图1所示。该方法可以实现对织物折皱形成与消失过程的自动化监测,并精确提取折皱动态参数,给出客观评价。首先,使用定制装置对织物进行加压释放处理,然后使用高速摄像机采集织物折皱回复过程中的图像序列,使用改进的KCF算法跟踪折皱区域,获取感兴趣的折皱部位图像。接着进行折皱区域图像二值化与骨架化处理,最后使用直线拟合函数和反、正切函数直接提取折皱关键点角度信息。通过对不同组织规格织物进行实验,获取各织物试样折皱回复过程中的折皱顶角角度信息,分析比较织物折皱回复性能。
1.2 传统KCF算法
1.2.1 传统KCF算法基本原理
KCF算法基本原理是构建一个核相关滤波器来实时跟踪视频序列中的目标。算法的关键在于利用核技巧将线性相关滤波推广到非线性空间,使图像特征可以映射到高维空间[10]。这样可以利用核方法提取目标的更多非线性特征,提高跟踪鲁棒性,通过在核空间中学习训练相关滤波器,使所得相关滤波器可以对新样本进行分类,具体算法流程如图2所示。
1.2.2 传统KCF算法在检测中的问题
经过预实验,发现直接应用KCF算法进行织物折皱顶角的跟踪主要存在以下两个问题:
算法使用单一HOG特征[16],对织物折皱顶角外观变形、光照变化等情况缺乏鲁棒性,容易导致跟踪目标丢失;跟踪框边界效应明显,在目标出现形变时无法有效捕捉边界信息,降低了跟踪精度,为后续顶角角度计算处理带来过多干扰。
1.3 改进KCF算法
为解决这两个问题,本文在传统KCF算法的基础上在特征表达和目标区域调整两个方面进行优化。在特征表达方面,采用了多特征融合的策略,同时结合HOG特征和SIFT特征来表达折皱顶角的纹理与轮廓信息,以提高检测鲁棒性。在目标区域调整方面,提出了一种基于边缘检测的自适应边界调整方法,根据检测到的边缘位置与方向信息,自适应调整跟踪框的大小与位置,以减小边界效应,提高定位精度。
1.3.1 多特征融合
为增强对织物折皱顶角的检测鲁棒性,本文采用了多特征融合的策略。具体来说,同时结合HOG特征和SIFT特征[17]来表达折皱顶角的纹理与轮廓信息。其中,HOG特征通过统计目标局部方向梯度直方图来描述形状;SIFT特征通过检测关键点与计算描述子来表示局部纹理。为降低特征维数,本文首先利用主成分分析(PCA)算法对HOG和SIFT特征进行降维处理,然后将经降维的两种特征拼接起来进行核相关跟踪,这样既提高了特征表达能力,又减少了计算量。假设原始的特征向量为x∈Rd(x属于d维实数空间),PCA的目标是找到一个变换矩阵W∈Rd×k,其中k是降维后的维度,使得投影后的特征向量y=WTx∈Rk最大化方差。具體来说,PCA可以通过以下步骤实现:
1)对所有的特征向量进行中心化,即将每个特征向量减去均值,得到:
X=xHOGxSIFT(1)
式中:xHOG∈RdHOG表示HOG特征向量,xSIFT∈RdSIFT表示SIFT特征向量。
通过在这两个向量上进行垂直拼接,得到了长为dHOG+dSIFT的列向量X,它将这两个特征向量中的信息一起编码成了一个单一的向量。假设通过PCA将这两种特征向量降至k维,得到降维后的特征向量为:
yHOG=WTHOGxHOG∈Rk(2)
ySIFT=WTSIFTxSIFT∈Rk(3)
式中:yHOG和ySIFT分别是HOG特征和SIFT特征的降维矩阵。
2)计算协方差矩阵:
Cy=1n∑ni=1yiyTi(4)
式中:n是样本数,yi是第i个样本的降维后的特征向量。
3)对协方差矩阵进行特征值分解,得到特征值和特征向量:
Cy=UΛUT(5)
式中:Λ=diag (λ λ …,λk)是特征值矩阵,U=[u u …,uk]是特征向量矩阵,且满足UTU=I。
4)选择前m个特征向量,组成降维矩阵:
U(:,1:m)(6)
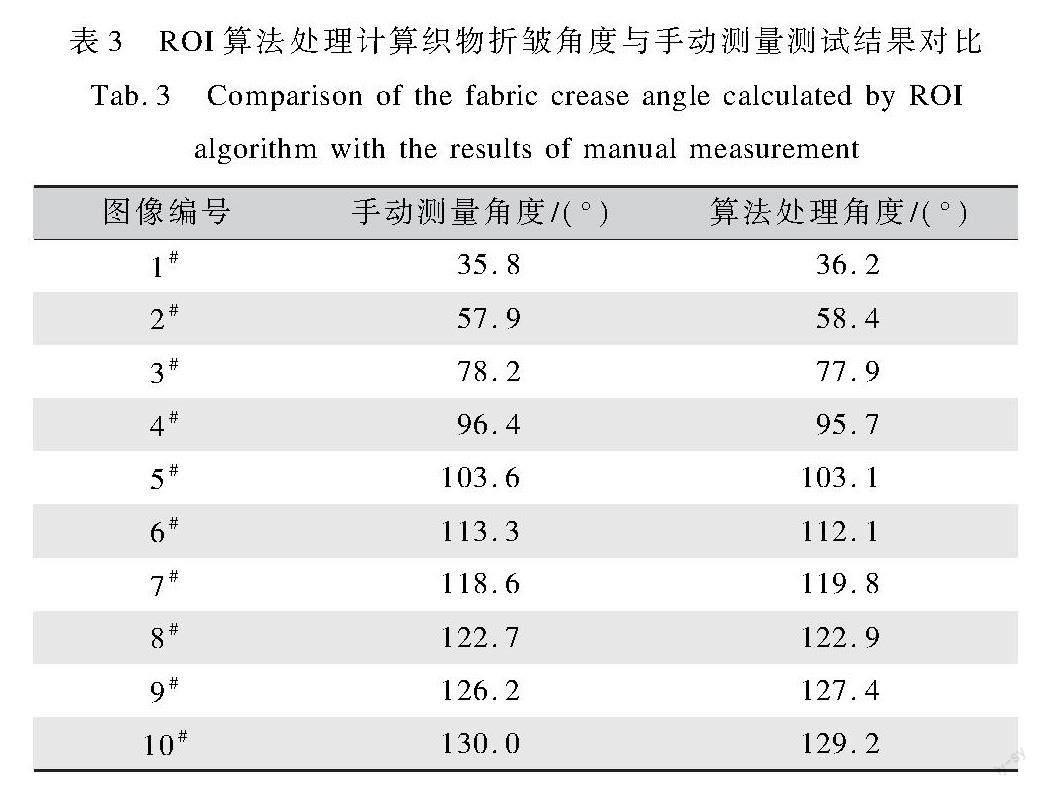
式中:m 5)将HOG特征和SIFT特征的降维矩阵分别乘以降维矩阵V,得到融合后的特征向量: yfusion=[yHOG,ySIFT]V∈R2k×m(7) 式中:[,]表示特征向量的拼接操作,yfusion是融合后的特征向量,维度为2k×m。 通过将HOG特征和SIFT特征进行PCA降维,并将降维后的特征向量融合,可以得到更加紧凑且表达能力更强的特征向量,从而提高图像识别的准确度。 1.3.2 基于边缘检测的自适应边界调整 为减小边界效应对跟踪精度的影响,本文提出了一种基于边缘检测的自适应边界调整方法。具体来说,利用Canny边缘检测算法检测折皱顶角的边缘轮廓,根据检测到的边缘位置与方向信息,自适应调整跟踪框的大小与位置,使其能够准确锁定目标边界。这样可以有效减小边界效应,提高跟踪精度。该方法包括以下几个步骤: 1)初始化目标跟踪框:在第一帧图像中,使用KCF算法初始化目标跟踪框,得到目标区域的中心位置(xc,yc)、宽度w和高度h。 2)检测目标边缘:在每一帧图像中,使用Canny边缘检测算法来检测目标的边缘,得到边缘的位置和方向(xe,ye)和θc。 3)计算目标区域的调整量:根据边缘的位置和方向,计算目标区域的调整量dw、dh、dx、dy,其中dw、dh表示目标区域的宽度和高度的调整量,可以根据边缘的宽度和高度以一定的比例进行计算;dx、dy表示目标区域中心位置的调整量,可以根据边缘方向的余弦和正弦值以一定的比例进行计算。 4)调整目标区域的大小和位置:根据目标区域的当前大小和位置,以及计算得到的调整量,自适应地调整目标区域的大小和位置。具体来说,可以使用下式进行计算: w′=w+α·dw h′=h+α·dh x′c=xc+α·dx y′c=yc+α·dy(8) 式中:α是调整步长,用于控制目标区域大小和位置的调整速度。 通过调整目标区域的大小和位置,可以减少边界效应的影响,提高目标跟踪的准确性。 5)更新目标跟踪器:使用新的目标区域大小和位置,更新KCF算法的目标跟踪器,继续跟踪目标。 1.4 ROI图像处理 为了获得织物折皱顶角角度信息,需要对经过KCF算法处理后获取的一系列ROI图像进行进一步处理,来提取折皱角度特征参数。首先进行图像二值化,使用Otsu方法[18]根据图像直方图确定一个全局阈值,对图像进行阈值分割,将图像中的像素分类为前景和背景两个部分以滤除背景噪声,突出折皱的轮廓特征。然后对二值化图像进行骨架化处理,使用Zhang-Suen算法[19]迭代腐蚀图像而保留拓扑结构,得到折皱区域的细化代表,以便突出折皱的拓扑形状,能够在保修角度信息的同时大大降低后续处理的复杂度。之后在骨架图像上使用最小二乘法拟合直线,并计算两条直线的夹角。本文采用简单高效的最小二乘法来进行几何特征拟合,既能提取出折皱顶点的角度信息,又避免了较为复杂的模型拟合。最后利用反正切函数求出两直线的夹角值,即为折皱顶点的角度。ROI图像通过上述处理可以从原始图像中有效提取出折皱回复研究所需的角度信息。 2 实 验 2.1 装置及操作方法 为实现对织物折皱回复全过程进行检测,本文自主设计并搭建了织物折皱回复测试装置,如图3所示。该装置主要由样品台、升高装置、加载装置、高速摄像机等组成。样品台采用光滑不锈钢材质,可以调节倾斜角度;升高装置和加压装置分别用于抬高和加压样品;高速摄像机最大帧率为960 fps,采集图像分辨率为1 280×1 024像素。测试过程使用气压传动作为动力系统。 本文选择了6种不同规格的面料作为试样,以全面评估所提出方法的鲁棒性和泛化能力。这些面料样本覆盖了不同的纤维类型、织物结构、厚度和密度,试样具体规格参数如表1所示。具体而言,选择的面料包括纯棉、涤纶、涤棉和亚麻等不同纤维类型,代表了常见服装面料的主要组成材质。此外,还选择了平纹、斜纹和方格等不同的基本织物结构,以检验织物组织对方法适用性的影响。不同规格的纱线和不同的织物密度也在选样范围内,以代表厚度和密度不同的织物材质。通过在这些具有差异性的参数的面料上进行测试,可以全面验证所提出方法的适用范围,以证明该方法的广泛适用性,不受具体面料参数的限制。实验操作前,对每種面料剪取10片大小为26 cm×15 cm的样品,所有样品在标准状态(温度20 ℃±2 ℃,相对湿度65%±5%)条件下放置24 h后进行测试。 通过预实验,本文发现将织物折皱回复检测装置参数设置为试样台倾斜30°,升高装置抬起升高15 cm,加压压力60 N,加压时间设定为60 s时,采集所选规格织物试样折皱回复过程图像更为理想。 使用织物折皱回复检测装置具体方法为:将试样固定在试样台上,其中试样23处与仪器升高装置线对齐。打开气阀开关,调整气压数值使气压表压力达到60 N;打开升高装置,将织物试样升起到指定高度之后,打开加压装置开关,使两端力臂对织物试样进行加压处理使其产生折皱。加载结束后,同时关闭升高装置和加载装置,使样品自由下落并开始折皱回复过程,高帧率摄像机记录织物下落过程中顶角折皱回复形变过程。在对织物进行加压折皱处理后,对折皱回复过程进行记录,使用改进KCF算法追踪并截取感兴趣区域内图像。在全过程中,高速摄像机以240 fps的速度对样品图像动态进行采集,随后每隔10帧从采集的图像序列中选取一帧进行算法处理。对每种面料随机选择5片样品进行测试。 2.2 基于改进KCF算法的折皱回复过程分析 利用改进的KCF算法处理高速摄像机采集的折皱回复图像序列,实现对面料折皱区的准确跟踪。首先选择面料折皱区顶点作为目标区域进行初始化,然后应用改进的KCF算法自动跟踪折皱顶点在复原过程中的运动轨迹。为增强跟踪鲁棒性,算法融合使用HOG和SIFT特征,并辅以Canny边缘检测调整目标区域。 为了验证改进KCF算法在研究中的必要性和有效性,本文使用改进KCF算法和传统KCF算法对相同织物折皱顶角图像序列进行测试,测试过程中部分图像如图4所示。其中红色虚线部分为传统KCF算法跟踪框,绿色部分为改进后的KCF算法跟踪框。由图4可以看出,相较于改进后的KCF算法,传统KCF算法在面对较大形变时,会出现跟踪丢失的情况。 对跟踪ROI部分进行截图(图5(a)),提取折皱顶点对应的图像区域。截取ROI图像的目的是精确定位感兴趣的折皱顶点区域,便于进行后续定量分析,并将ROI图像转化为二值化图像(图5(b))。进行二值化处理是为了滤除背景及不相关区域,突出折皱顶点的轮廓特征,简化形状表达。使用骨架提取算法处理二值图像可以得到折皱区域的细化(图5(c))。骨架提取通过细化可以有效保留目标区域的拓扑结构,本文采用Zhang-Suen算法进行骨架提取。该算法计算开销较低,易于实现,能够有效细化折皱顶点区域,突出其角度特征。对细化后骨架图像使用直线拟合函数进行拟合计算,并使用反正切函数求出两直线夹角角度,即折皱顶点角度。通过对骨架使用简单的几何特征拟合,可以提取折皱顶点角度这一定量参数,便于进行动态跟踪分析。对每帧图像重复该过程,获得不同面料样品折皱顶点角度变化规律,并进行对比分析。 3 结果与分析 3.1 改进KCF算法有效性验证 为了验证算法准确性和有效性,本文将基于多特征融合和自适应边界调整的改进KCF算法与传统KCF算法在VOT-2016(Visual Object Tracking, 2016)数据集上进行对比测试。VOT-2016数据集是一个用于视觉目标跟踪算法评估的公开数据集,并且提供了一套评估指标,用于定量地评估算法的性能,包括准确性、鲁棒性和速度等方面。实验操作系统环境为:64位专业版Windows 11操作系统,Python 3.9. AMD5800H,NVIDIA RTX3080Ti,16 G内存;本文选取ROC曲线(Receiver Operating Characteristic Curve)下的面积AUC(Area Under Curve)、追踪成功率SR(Success Rate)及每秒处理帧率FPS作为对比参考指标,其中各指标定义及计算方法如下: 1)AUC指标:AUC指Area Under Curve,代表ROC(Receiver Operating Characteristic)曲线下的面积值。它通过在不同阈值下计算真正率和假正率,即在二分类问题中,被正确地预测为正例的样本数量与实际正例样本数量之间的比例和被错误地预测为正例的负例样本数量与实际负例样本数量之间的比例,进而绘制ROC曲线。曲线下面积值越大,表示分类性能越好。其计算方法是将ROC曲线下的面积数值化到0~1。 在本文中,AUC指标反映了改进KCF算法在不同判定阈值下的检测精度,值越大表示检测准确率越高。 2)SR指标:SR表示Success Rate,代表跟踪成功率。它是跟踪过程中成功跟踪帧数占总帧数的比例,计算方法为: SR=NsuccessNtotal(9) 式中:Nsuccess和Ntotal分别代表成功追踪到目标的帧数和总帧数。 SR指标反映了目标跟踪的稳定性,SR值越大表示改进算法跟踪更加稳定可靠。 3)FPS指标:FPS代表每秒处理帧数(Frame Per Second),计算方法为: FPS=NframesTtotal(10) FPS指标反映了算法的处理效率。本文中,FPS值越大表示改进算法在保证精度的前提下,处理帧数越多,实时性越好。 传统KCF与本文改进KCF在VOT-2016数据集测试结果对比如表2所示。 由表2的数据可以看出,在VOT-2016数据集上的测试中,相比原始的KCF算法,加入HSP(HOG+SIFT+PCA)模块和ABT(Adaptive Boundary Tuning)模块的KCF+HSP+ABT算法效果最好,AUC指标反映检测准确率,本文改进算法KCF+HSP+ABT的AUC值为0.785,较原始KCF算法的0.463显著提高了69.5%。这表示融合多特征和自适应调整技术大大提高了检测精度,使得算法在织物折皱顶角跟踪过程中对目标的提取和定位更准确,有效降低因传统算法边际效应带来的织物折皱顶角部分图像跟踪丢失的比率。SR指标反映跟踪稳定性,本文改进算法的SR为0.68 较KCF的0.396提高了72.2%。这意味着改进算法明显增强了对织物折皱顶点的跟踪鲁棒性,说明HSP和ABT模块对提升KCF算法的鲁棒性与准确率有积极作用,也证明在整个目标跟踪过程中,改进后的KCF算法更加稳定可靠,对于织物折皱动态回复过程的提取更加完整。另外,对于追踪织物顶角任务,改进算法的FPS下降在可接受范围内,考虑到性能指标的大幅度提升,该计算代价可接受。 3.2 ROI处理算法有效性验证 为保证算法的速度和精确度,本文对上述ROI图像处理过程进行实验。在速度测试部分,测试环境与系统环境保持一致,在该环境下算法处理一帧ROI图像的平均速度为20 ms,考虑到每秒需处理24帧图像,该算法满足测试速度需求;在算法准确性测试部分,本文对1#织物试样进行实验处理,将1#织物试样折皱回复过程每隔1.5 s记录一次,选取其中连续记录的10帧顶角图像分别使用算法测量和人工手动测量进行对比测试,测试结果如表3所示。计算其平均误差为0.70°,测试结果表明对ROI图像的处理算法可以滿足实际检测需要。 同时表3数据也可以看出,织物试样在开始阶段折皱回复形变速度较快,后续逐渐减缓,逐渐趋于稳定的回复过程。这反映出1# 织物试样折皱回复的动态演变过程,不同阶段的折皱形态也可以通过顶角角度数据量化反映。 3.3 测试方法与标准方法测试结果对比 为验证该方法有效性,本文选取该方法下不同织物在回复稳定状态下同一时刻的顶角角度与标准织物折皱回复角检测法测得结果进行对比。按照AATCC 66—2017《机织物折皱回复:回复角法》标准检测要求对所选织物试样折皱回复性进行检测,检测结果与本文方法所得结果对比如表4所示。 经过相关性检验,两者的皮尔逊相关系数为0.857 (大于0.500),显著性水平为0.000 4(小于0.01),说明两种方法所得测试结果之间存在较强正相关,呈现高度的线性相关关系。经过计算,两种方法所得结果相关系数R2为0.73 R2较高说明本文方法所得结果可以与标准折皱角检测方法结果很好拟合。使用线性回归计算出二者存在一元线性模型: Y=0.549×X+34.754(11) 式中:X为ROI区域织物顶角角度,Y为标准方法测量的织物折皱回复角平均值。 该结果验证了基于改进KCF算法的动态折皱回复检测方法能够有效反映面料折皱回复性,测试结果与标准方法具有可比性,可以作为一种新的折皱回复性能评价手段。 4 结 论 本文提出了一种基于改进KCF算法的动态织物折皱回复检测方法。对传统KCF算法在织物折皱回复检测任务中的问题,提出了两种优化策略。第一是采用多特征融合的方法,综合运用HOG、SIFT等特征表达,增强了算法对织物纹理的适应性,提高了检测鲁棒性。第二是基于Canny边缘检测结果进行自适应目标区域调整,有效减小了边界效应,提高了定位精度。两种策略相互协同,形成了一种改进的KCF算法。实验结果表明,该改进算法相比原KCF方法,在处理织物折皱动态回复图像序列时性能提升显著,其中AUC指标达到0.78 相较于原KCF算法提高了69.5%;SR指标达到0.68 相较于原KCF算法提高了72.2%,这验证了所提出的两种优化策略的有效性。本文整套测试方法流程实现了对整个折皱回复过程的自动监测与分析,基于该改进算法,实现了对不同织物折皱回复过程的自动化监测和参数化分析,方法检测结果与标准测试结果具有很好的一致性(R2=0.736)。相比传统折皱回复角测试法,该方法实现了对折皱回复动态过程的精确捕捉,测量结果平均误差控制在0.70°,大幅提高了检测效率与结果可重复性,该方法无需人工参与,检测周期短,提供了一种更为高效准确的织物折皱回复性能评估新思路。后续工作将进一步增强算法鲁棒性,并扩展应用到包括服装面料在内的更多织物折皱回复检测。 参考文献: [1]韩茹. 影响棉织物折皱回复性因素的探讨[J]. 轻工科技, 2015, 31(10): 92-93. HAN R. Discussion on factors affecting the wrinkle recovery of cotton fabrics[J]. Light Industry Science and Technology, 2015, 31(10): 92-93. [2]魏艳红, 刘新金, 李文静, 等. 几种不同组织结构的衬衫面料保形性研究[J]. 丝绸, 2020, 57(1): 20-25. WEI Y H, LIU X J, LI W J, et al. Study on shape preservation of shirt fabrics with several different weave structures[J]. Journal of Silk, 2020, 57(1): 20-25. [3]張小琪. 形状记忆纺织品和遮热纺织品检测方法的研究[D]. 上海: 东华大学, 2018. ZHANG X Q. Testing Methods for Shape Memory Fabric and Thermal Shielding Fabric[D]. Shanghai: Donghua University, 2018. [4]蒋双歌, 王蕾, 王静, 等. 织物折皱回复的各向异性表征[J]. 纺织学报, 2016, 37(6): 42-47. JIANG S G, WANG L, WANG J, et al. Characterization on anisotropy of fabric wrinkle recovery[J]. Journal of Textile Research, 2016, 37(6): 42-47. [5]杨书会. 基于织物结构与力学参数的纯棉织物抗皱性能研究[D]. 天津: 天津工业大学, 2017. YANG S H. Research on Wrinkle Resistance of Cotton Fabrics Based on Fabric Structure and Mechanical Parameters[D]. Tianjin: Tiangong University, 2017. [6]刘婷, 刘成霞. 织物多向抗皱性分析研究[J]. 毛纺科技, 2015, 43(12): 47-51. LIU T, LIU C X. Wrinkle resistance test research and analysis of fabric in multi-angle[J]. Wool Textile Journal, 2015, 43(12): 47-51. [7]唐千惠, 王蕾, 高卫东. 基于图像处理的织物保形性检测[J]. 纺织学报, 2021, 42(3): 89-94. TANG Q H, WANG L, GAO W D. Detection of fabric shape retention based on image processing[J]. Journal of Textile Research, 2021, 42(3): 89-94. [8]姚金波, 王志意, 董敏, 等. 温湿环境下棉织物的抗皱性能变化规律及其预测模型[J]. 天津工业大学学报,202 39(5):43-49. YAO J B, WANG Z Y, DONG M, et al. Change and prediction model of crease resistance of cotton fabric under warm and humid environment[J]. Journal of Tiangong University, 2020, 39(5): 43-49. [9]唐千惠, 王蕾, 傅佳佳, 等. 织物保形性检测系统开发初探[J]. 棉纺织技术, 2020, 48(5): 31-34. TANG Q H, WANG L, FU J J, et al. Primary investigation of fabric conformality detection system[J]. Cotton Textile Technology, 2020, 48(5): 31-34. [10]HENRIQUES J F, CASEIRO R, MARTINS P, et al. Exploiting the circulant structure of tracking-by-detection with kernels[C]. Providence, RI, USA: IEEE Conference on Computer Vision and Pattern Recognition, 2012. [11]张薇, 康宝生. 相关滤波目标跟踪进展综述[J]. 中国图象图形学报, 2017, 22(8): 1017-1033. ZHANG W, KANG B S. Recent advances in correlation filter-based object track[J]. Journal of Image and Graphics, 2017, 22(8): 1017-1033. [12]BOLME D S, BEVERIDGE J R, DRAPER B A, et al. Visual object tracking using adaptive correlation filters[C]The 23th IEEE Conference on Computer Vision and Pattern Recognition. San Francisco, USA: IEEE, 2010. [13]BERTINETTO L, VALMADRE J, GOLODETZ S, et al. Staple: Complementary Learners for Real-time Tracking[C]. Las Vegas: Proceedings of IEEE Conference on Computer Vision and Pattern Recognition, 2016. [14]潘長城, 刘妍妍, 郑志强, 等. 类残差更新策略的核相关滤波目标跟踪[J]. 电光与控制, 2019, 26(10): 1-6. PAN C C, LIU Y Y, ZHENG Z Q, et al. Kernel correlation filtering target tracking based on quasi-residua updating strategy[J]. Electronics Optics & Control, 2019, 26(10): 1-6. [15]孙晓锋, 贾子彦, 张雷, 等. 基于重检测机制的核相关滤波跟踪算法[J]. 电光与控制, 2021, 28(8): 44-47. SUN X F, JIA Z Y, ZHANG L, et al. A kernel correlation filter tracking algorithm based on re-detection mechanism[J]. Electronics Optics & Control, 2021, 28(8): 44-47. [16]DALAL N. Histograms of oriented gradients for human detection[C]International Conference on Computer Vision & Pattern Recognition. San Diego, CA, USA: IEEE Computer Society, 2005. [17]LOWED G. Object Recognition from local scale-invariant features[C]Proceedings of the Seventh IEEE International Conference on Computer Vision. Bombay, India: IEEE, 1999. [18]OTSU N. A Threshold selection method from gray-level histograms[C]IEEE Transactions on Systems, Man, Cybernetics. Philadelphia, PA, USA: IEEE, 1979. [19]CHEN Y S, HSU W H. A modified fast parallel algorithm for thinning digital patterns[J]. Pattern Recognition Letters, 1988, 7(2): 99-106. Research on fabric wrinkle recovery detection based on an improved KCF algorithm GUO Xuyuan1, LI Zhongjian2, WANG Lei1, PAN Ruru1, GAO Weidong1 ( 1.Key Laboratory of Science & Technology of Eco-Textile, Ministry of Education, Jiangnan University, Wuxi 214122, China; 2.Key Laboratory of Clean Dyeing and Finishing Technology of Zhejiang Province, Shaoxing University, Shaoxing 312000, China) Abstract:Fabric wrinkle recovery performance is an important indicator for evaluating the shape retention of fabrics. It reflects the ability of fabrics to spontaneously recover their original shape after wrinkling during use and processing. Good wrinkle recovery performance enables fabrics to quickly recover after folding, transportation and cutting, thereby improving utility. The currently widely used standard method for evaluating fabric wrinkle recovery performance is the wrinkle recovery angle test. This involves folding and pressing fabric samples and then measuring the angle of recovery for the resulting creases to assess the fabrics wrinkle recovery capability. However, this method is complex to operate, relies on manual judgment and measurement for testing, yields results vulnerable to subjective effects, and cannot distinguish or quantify the dynamic evolution of wrinkles during different recovery stages. It can only provide an approximate overall evaluation and fails to accurately describe wrinkle recovery patterns in detail. Therefore, there is a need to develop a new testing method to achieve automated monitoring and quantified parameterization analysis of the entire wrinkle recovery process, in order to more efficiently, precisely and comprehensively evaluate the wrinkle recovery performance of different fabric materials and provide a basis for fabric performance optimization. In view of this, this study proposed a fabric wrinkle recovery detection method based on an improved kernel correlation filter algorithm to achieve automated monitoring and key parameter extraction of the entire fabric wrinkle recovery process. As for the method, a high-speed camera was used to collect and record images throughout the dynamic process of the formation and recovery of fabric wrinkles and a set of detection system was designed to process and analyze the image sequence. In the system, a robustness-enhanced improved KCF algorithm was first applied to track and locate fabric wrinkle areas. This algorithm improved adaptation to texture and shape changes by fusing multiple feature expressions and employed an edge adaptive adjustment algorithm to reduce boundary effects. Next, morphological binarization and skeleton extraction were performed on the wrinkle area of interest to preserve the topological structure while simplifying structural expression. Finally, based on the principles of analytic geometry, polyline fitting was performed on the skeletonized graphical shapes to calculate the vertex angle parameter, thereby obtaining time-series data on the variation of the wrinkle peak angle over time. The method achieved automated monitoring of the entire fabric wrinkle recovery process, avoided subjective judgment, and greatly improved detection efficiency, enabling detection and record of fabric crease recovery at different stages. By comparing the results obtained by this new method with those obtained by the standard wrinkle recovery angle test method, it is found that the two test results have strong correlation, which verifies the effectiveness of this new method and shows that this method can be used as a new technical means to evaluate the crease recovery performance of fabrics more accurately and comprehensively. This study establishes detection technology and analysis methods that lay the foundations for building an intelligent fabric wrinkle recovery evaluation platform going forwards. Future work will progress in the following areas: (i) to continue to improve algorithm robustness to address detection issues under conditions involving light, occlusion, etc.;(ii) to expand the algorithms scope of application to enable generalized detection across more fabric types; (iii) to collect and annotate large quantities of dynamic wrinkle process data to train deep neural network models for intelligent analysis of fabric wrinkle morphology to support structural design and performance enhancement of fabrics. Progress in the above areas will make testing methods more efficient and precise, promote advances in wrinkle recovery evaluation techniques, and provide new ideas to improve fabric structural design and performance. Key words: wrinkle recovery angle; feature fusion; target tracking; kernel correlation filter; improved KCF

