织物和静电极板参数对静电吸附力的影响分析

王青 党帅 盛晓超 吕绪山 姜越夫 赵恬恬

Analysis of the effect of fabric and electrostatic pole plate parameters on the electrostatic adsorption force

摘要：为了明确织物和静电极板参数对静电吸附力的影响规律，为服装软面料的静电吸附式抓取提供理论支撑，文章开展织物参数和静电极板参数对静电吸附力影响规律的系统性研究。首先建立纬编织物结构模型及静电吸附力理论模型，通过理论分析结果和仿真结果的对比分析，验证仿真方法的有效性；接着基于Maxwell张量法推导了五层二维静电吸附力理论模型，分析静电吸附力模型结构参数对静电吸附力的影响规律，并得出结论：1）静电吸附力和电极上施加电压的平方成正比；2）织物密度越大，产生的静电吸附力越大；3）绝缘层介电常数越大，静电吸附力越大；绝缘层厚度越大，静电吸附力越小；4）随着极板占空比及电极间距的增大，静电吸附力均呈先增大后减小的趋势。

关键词：面料抓取；织物建模；叉指状电极；静电极板；静电吸附力；Maxwell

中图分类号：TS181.8

文献标志码：A

文章编号：10017003（2024）04007108

DOI：10.3969j.issn.1001-7003.2024.04.009

收稿日期：20230506;

修回日期：20240312

基金项目：国家自然科学基金项目（52105584）

作者简介：王青（1985），女，博士，讲师，主要从事智能纺织设备开发与研究。

纺织服装生产过程中，由于面料具有高弹、透气、轻质和柔性等特点，目前其抓取转移过程主要依靠人工来完成，这并不符合智能化发展趋势。当下能够实现服装面料抓取和转移的方法主要有机械手抓取［1-2］、针刺抓取［3］、负压吸盘式抓取［4］和静电吸附式抓取［5］几种。其中机械手抓取与针刺抓取过程容易对面料造成不同程度的破坏；负压吸盘式的抓取方式在抓取不同透气性的面料时吸附力不稳定，且在抓取透气性高的面料，能耗与噪声过大；静电吸附式的抓取方式则因吸附力稳定、抓取定位精度高，成为较为理想的抓取方式［6］。

鉴于静电吸附技术的优势，学者们开展了一系列相关研究工作，主要集中于静电吸附式爬壁机器人的设计研究、静电吸附式机械手的研究及静电吸附技术的理论研究等。Yamamoto等［7］设计了一种基于静电吸附的爬壁装置，并测试了该装置在导电与非导电壁面的附着性能，发现吸附力与施加电压的平方成正比；Sogard等［8］根据库伦作用及J-R卡盘力评估了静电吸盘的夹持性能；Berengueres等［9］通过将静电卡盘吸附力与壁虎脚面粗糙度自适应功能相结合，提出一种新型爬壁系统；Dhelika等［10］提出了一种双极型静电夹持器，分析了粗糙表面对吸附力的影響，并实现了物体的抓取与转移放置操作；Guo等［11］利用电流变凝胶作为阵列电极绝缘介质层，改善对易变形、致密性差的材料吸附性能；在极板结构优化方面，王黎明等［12］分析了静电吸附原理，并建立了静电极板与壁面之间的吸附力建模，最终通过实验验证了其静电吸附作用的存在，且对极板性能进行优化；陈辉云等［13］对静电吸附力的主要影响因素进行了分析，并针对不同的抓取物件设计了两种类型的静电吸附抓手；刘立东等［14］以服装面料为抓取对象，研究了极板部分结构参数对静电吸附力的影响，提出通过增加电极板边缘长度来实现叉指电极的电容增长，并成功将静电极板的吸附能力提高了10%。

综上分析，虽然基于静电吸附技术的应用研究较多，但以服装面料为抓取对象的研究还很少，且缺乏静电极板结构参数和织物参数对静电吸附力影响的系统性分析。因此，本文以纬编织物为抓取对象，系统研究织物参数和静电极板结构参数对静电吸附力的影响规律，以期为静电极板的设计和优化提供理论参考。

1  静电吸附模型的建立

1.1  织物模型建立

日常生活中大部分的针织物都是由纬编织物单元阵列组合而成，纬编织物单元结构是决定针织物内在性质和外观特征的主要因素。目前，国内外纬编织物建模主要采取Pierce建模法、非均匀有理B样条曲线（NURBS）建模法等［15］。Pierce线圈模型主要由针编弧、沉降弧及圆柱三个部分构成，是比较理想化的模型，故与真实织物存在较大差异［16］；非均匀有理B样条（NURBS）法建立的织物模型，具有数据精确、结构灵活的特点，更加贴近织物的真实结构形态［17］。因此，本文采用非均匀有理B样条（NURBS）建模方法对纬编织物单元进行建模。

建立三维坐标系，参数u、v、w分别作为坐标系的横轴、纵轴、竖轴，并于坐标系中添加织物单元控制点，依次记为P1～P16。其中P5～P8点对应织物单元针编弧，P13～P16对应下个织物单元的针编弧，P1～P3与P10～P12控制点分别对应左右两侧沉降弧，剩余控制点则对应织物单元圆柱。

设纬编织物单元线宽为W，线高为H，圈深为D，织物单元控制点空间坐标则为：

Pi=（kWWu，kHHv，kDDw）（1）

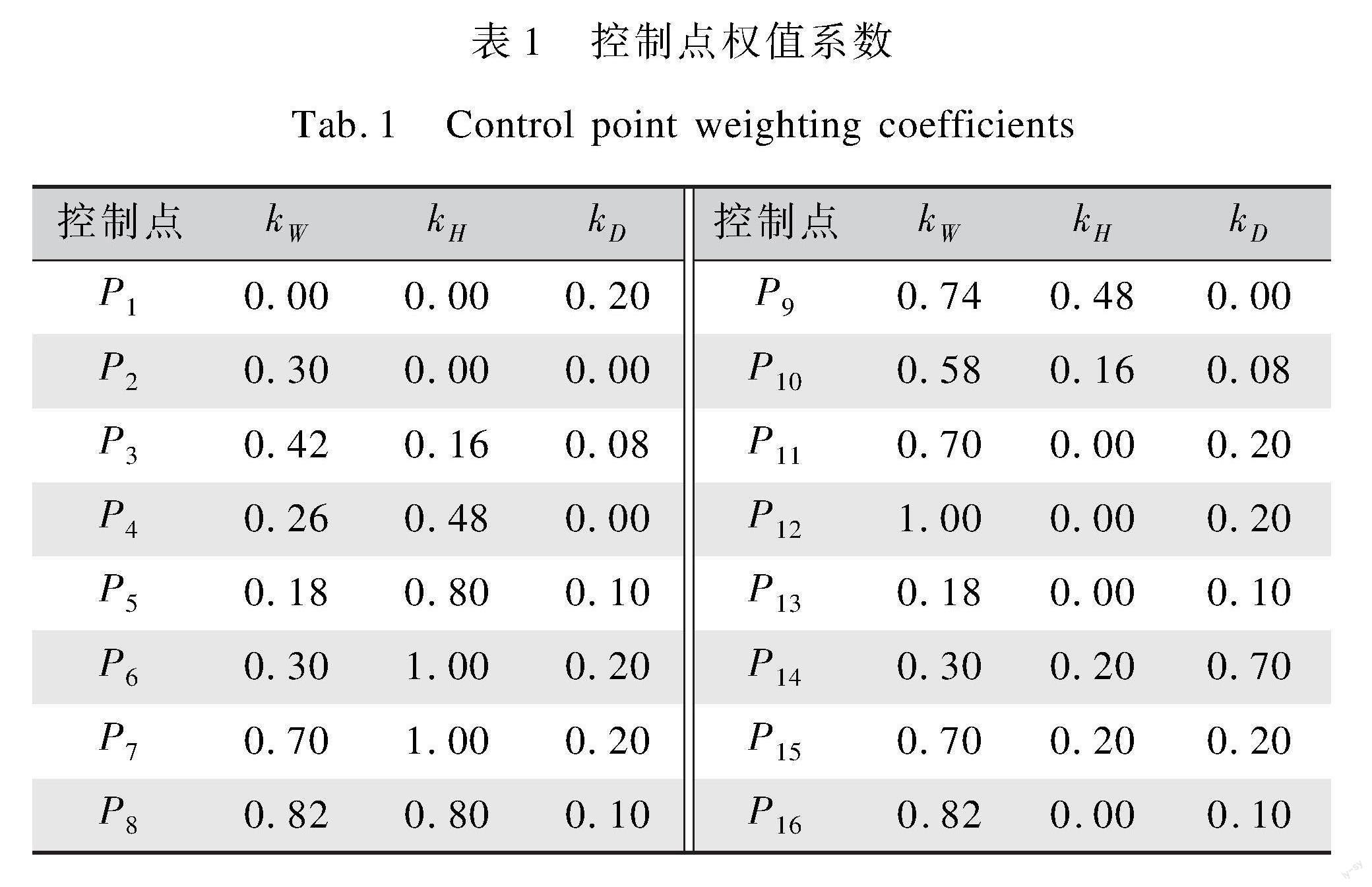
式中：kW、kH、kD分别表示控制点线宽、线高、圈深所对应权值系数，用于控制对应点与线圈尺寸的比例，各控制点所对应的权值系数取值如表1所示。

采用3次NUBRS曲线建模法，借助三维建模软件，结合各控制点确定织物单元各段中心线，并赋予其对应截面，扫掠后构成纬编织物线圈单元实体模型，最终经过阵列形成纬编织物面结构模型，如图1所示。

1.2  极板选型与静电吸附理论模型

1.2.1  极板选型

吸附电极分为单极型和双极型两种。单极型电极由金属极板和两侧绝缘介质层组成，金属极板接正向电压，置物台接负向电压，形成极化电场，使得织物层内正负电荷重新排布，从而实现吸附效果；双极型电极由正、负电极构成，处于同一平面，多采用镶嵌式结构，吸附原理与单极型相同，但无需额外的辅助电极即可实现吸附效果。

相比于单极型吸附电极，双极型吸附电极具有更快的反应时间，对吸附与放置过程有更好的控制，而且静电弛豫现象不明显，可大幅提高吸附电极在工业生产过程中的安全性，是较理想的吸附电极选型。双极型吸附电极包括同心圆、方螺旋、希伯特曲线和叉指状电极等几种拓扑结构［18］，叉指状电极由于可在内部产生更大的平均电场，且更多的电极对数可形成更均匀的吸附力，更适合于抓取服装面料。因此，本文采用具有叉指状拓扑结构的双极型吸附电极。

1.2.2  静电吸附理论模型

双极型吸附电极所产生的总电场强度E为电极板所产生的电场强度和介质极化后产生的退极化电场强度的叠加，表示为：

E=E0－E1－E2－E3（2）

式中：E0、E1、E2、E3分別为吸附电极所产生的电场强度和绝缘介质层、空气层和织物层所形成的退极化电场强度。

退极化电场强度由高斯定理可表示为：

Ei=Eχi（3）

式中：Ei为被极化层产生的退极化电场强度， χi为被极化层的电极化率。

电极化率与该层介电常数有如下关系：

εi=1+χi（4）

式中：εi为被极化层介电常数。

整理式（2～4）可得总电场强度E表达式为：

E=E0εc+εa+εf－2（5）

式中：εc、εa、εf分别表示绝缘介质层、空气层与织物层的相对介电常数。

通过分析电偶极矩为p→的电偶极子在静电场中的受力情况，与织物层中电偶极子所对应的电偶极矩，可得到织物层中电偶极子所受静电吸附力为：

F=l（εf－1）εc+εa+εf－2ΔE02（6）

式中：l为织物层厚度；ΔE02表示沿极板方向电场强度的增减程度，Vm。

ΔE20求解参考文献［19］中圆环等效的方法，计算公式为：

ΔE20=∫+SymboleB@0  32εrrUh（h2+r2）52dr2（7）

式中：r、h分别为圆环半径与织物距离极板的间距，εr为等效介电常数，U为极板施加电压。

将式（7）代入式（6），可得静电吸附力为：

F=l（εf－1）εc+εa+εf－2∫+SymboleB@0  32εrrUh（h2+r2）52dr2（8）

1.3  仿真验证

由式（8）可以看出，静电吸附力F与织物层厚度l、电极板两端电压U及织物层距极板间距h等参数有关。为确保后续采用仿真模拟方法的有效性，设定l、εf及h等参数为定值（其中εf与织物中各纤维的体积百分比、几何形态有关，本文取为固定数值4），运用COMSOL Mutiphysics软件分析U对F的影响情况，将分析结果与式（8）的理论分析结果进行对照，得到F与U的曲线，如图2所示。

图2曲线表明，理论分析结果和仿真结果曲线趋势相同，即单位体积的静电吸附力F随着织物和极板电压U的增大而增大，但两曲线又存在一定偏差，且随着间距U的增大，偏差比例增大。分析原因，认为理论模型忽略了边缘效应，因此导致仿真结果与理论结果存在误差。

上述分析结果表明，织物结构在电场中确实会受到静电吸附力的作用，同时证明了仿真模拟方法的有效性和可行性。因此，后续将主要采用仿真模拟方法来进行静电极板参数对静电吸附力的影响分析。

2  结构参数对静电吸附力的影响分析

在前述研究中，采用了三维静电吸附理论模型，验证了当极板电压U增大时，静电吸附力增加的趋势，证明了织物在电场中会受到静电吸附力的作用，同时也验证了仿真模拟方法的有效性。然而，式（8）主要分析的是静电吸附模型外部调节参数（如织物厚度l、极板外接电压U与织物距离极板的间距h等）与静电吸附力之间的关系，不能体现静电吸附力模型内部结构参数对静电吸附力的影响。因此，将构建一种五层的二维静电吸附力模型，通过应用Maxwell应力张量方法，深入探究吸附模型中各参数对吸附力的影响规律。

2.1  静电吸附力模型建立

选取双极型叉指静电吸附模型的一个截面，在此基础上建立一个二维静电吸附力模型。由于该模型中正负电极周期性交替排列，故只选取一个周期进行建模和分析。采用COMSOL Multiphysics仿真软件，选择ACDC物理场中静电模块进行稳态研究。模型中电极宽度及电极对宽度分别设置为2a与2b；电极间距为t（t=2（b－a））；电极厚度忽略不计，施加电压分别为U和－U；占空比为k（k=ab）；吸附电极与织物层之间的气隙厚度为h；同时织物层具有孔隙，且不同结构和不同孔隙大小的织物层其织物密度不同，此处以覆盖系数η表征织物密度大小；空气、织物层、绝缘介质层和基底介电常数分别为εa、εf、εc和εs。建立双极型单周期静电吸附力模型，如图3所示。

织物层表面的静电吸附力，主要由施加的非均匀电场及极化电荷提供，所受静电吸附力可通过Maxwell应力张量法计算［20］，其公式为：

Tij=εEiEj－12δij|E|2（9）

式中：ε表示介电常数，δij表示张积量，Ei、Ej表示电场i、 j方向的分量。

沿织物层表面法线方向的吸引力FN通过对织物层表面上麦克斯韦应力张量Tij进行积分求得。假设吸附电极与织物层相互平行，长度为2b、覆盖系数为η的织物层上，静电吸附力的计算公式为：

FN=∮V fydv=∮STyyds=12εa∫2b0［（E23y－E23x）－（E21y－E21x）］dl（10）

式中：E1x和E1y分别表示绝缘介质层表面x与y方向上的电场分量，E3x和E3y分别表示织物层表面x与y方向上的电场分量。

整理得吸附模型上平均吸附力为：

σab=12εaεfεa2－1C（ab，h1b，hb，εcεf，η）U2b2（11）

式中：C（ab，h1b，hb，εcεf，η）为无量纲函数，受ab、h1b等因素影响，无实际物理含义。

式（11）也表明，静电吸附力与电极板施加的电压平方成正比，与1.2.2的推断一致。

2.2  理论模型验证

为验证上述理论模型的可行性，借助COMSOL Multiphysics软件分别构建文献［21］与文献［22］中相同结构构型的静电力吸附模型，且依次称为A吸附模型与B吸附模型。在A模型设计中，设定靜电吸盘的介电层厚度分别为123 μm和228 μm，并选择环氧树脂作为介电层材料（介电常数εc=7.8），基底层厚度为105 μm，采用了玻璃环氧树脂作为基底层材料（介电常数εc=4.2），铜电极厚度为35 μm，宽度为1 mm，最终将一块厚度为105 μm的硅晶片作为被吸附对象；在B模型设计过程中，设定静电吸盘的介电层厚度分别为33、133 μm和233 μm，并选择聚二甲基硅氧烷（PDMS）作为介电层材料（介电常数εc=3），基底层厚度为20μm，采用了聚酰亚胺（PI）作为基底层材料（介电常数εc=2.8），铜电极厚度为17 μm，宽度为2 mm，电极间距为100 μm，最终将一块纸张与丙烯酸的黏合体作为被吸附对象。

通过仿真验证，得到了静电吸附力的仿真结果与实验结果［21-22］对比曲线，如图4所示。对比曲线表明：仿真结果与实验结果变化趋势相一致，但具体数值存在一定偏差。分析数值偏差产生的原因包括实验过程中可能存在制作静电极板的不完美而导致产生误差，如基材与铜膜之间存在一定的气泡；此外，环境因素如温度、湿度等，也可能导致仿真结果和实验数据之间存在一定偏差。仿真结果和实验数据对比结果表明，本文提出的理论模型具有一定的可信度。因此，本文将基于此理论模型进行进一步的仿真分析。

2.3  参数对静电吸附力的影响分析

在COMSOL Multiphysics中建立五层静电吸附力模型，如图3所示。前文已经讨论过U对吸附力的影响，故此处设其为定值。设定静电极板施加的电场U为2 000 V［23］，电场频率f=100 Hz，此时织物介电常数εf不随织物层覆盖系数η的变化而显著变化［24］，因此后续研究均不考虑织物介电常数εf对静电吸附力的影响。则式（11）中C（ab，h1b，hb，εcεf，η）简化为C（ab，h1b，εcεf，η），后文将统一称作C，即可通过C随参数的变化情况间接反映单位长度上吸附力σab的变化情况，以此来探究静电吸附力模型结构参数与静电吸附力之间的关系。接下来，将采用控制变量方法，分别研究电极宽度a、绝缘介质层厚度h1、绝缘介质层介电常数εc和织物层覆盖系数η对参数C的影响，其中以绝缘介质层介电常数εc作为研究的基础，旨在减少仿真计算的次数，以及更加清晰地观察静电吸附力模型各参数对静电吸附力的影响效果。

2.3.1  εc与η对参数C的影响分析

设定εf与k（k=ab）分别为4ε0、0. h1b为0.0 研究极板绝缘层介电常数εc与织物覆盖系数η对静电吸附力的影响情况，其结果曲线如图5所示。

由图5可知，当η一定时，随着εc的增大静电吸附力相应变大，即绝缘层介电常数越大，所产生的静电吸附力越大；当εc一定时，η越大对应的静电吸附力越大，如εcεf为1时，η每增加0. 对应的C依次增大93%、40%、21%，即随着η的增加，所带来的静电吸附力增益逐渐减小。但整体而言，η与静电吸附力呈正相关关系，即织物越密，所产生的静电吸附力越大。

2.3.2  h1与εc对参数C的影响分析

设定εf与k分别为4ε0、0. 织物层覆盖系数η为0. 2b=2 mm，研究h1与εc的变化对参数C的影响情况，通过仿真模拟得到变化曲线，如图6所示。

由图6可知，当h1一定时，随着εc的增大静电吸附力也相应变大，和前文分析结果一致；当εc一定时，h1越大对应的静电吸附力越小，如εcεf为1时，h1b每增加0.0 对应的C依次减小27%、20%、15%，即随着h1b的增加，所带来的静电吸附力减益逐渐减小，但整体而言h1b与静电吸附力呈负相关关系。此处b为定值，因此绝缘介质层厚度h1越大，所产生的静电吸附力越小。

2.3.3  k与εc对参数C的影响分析

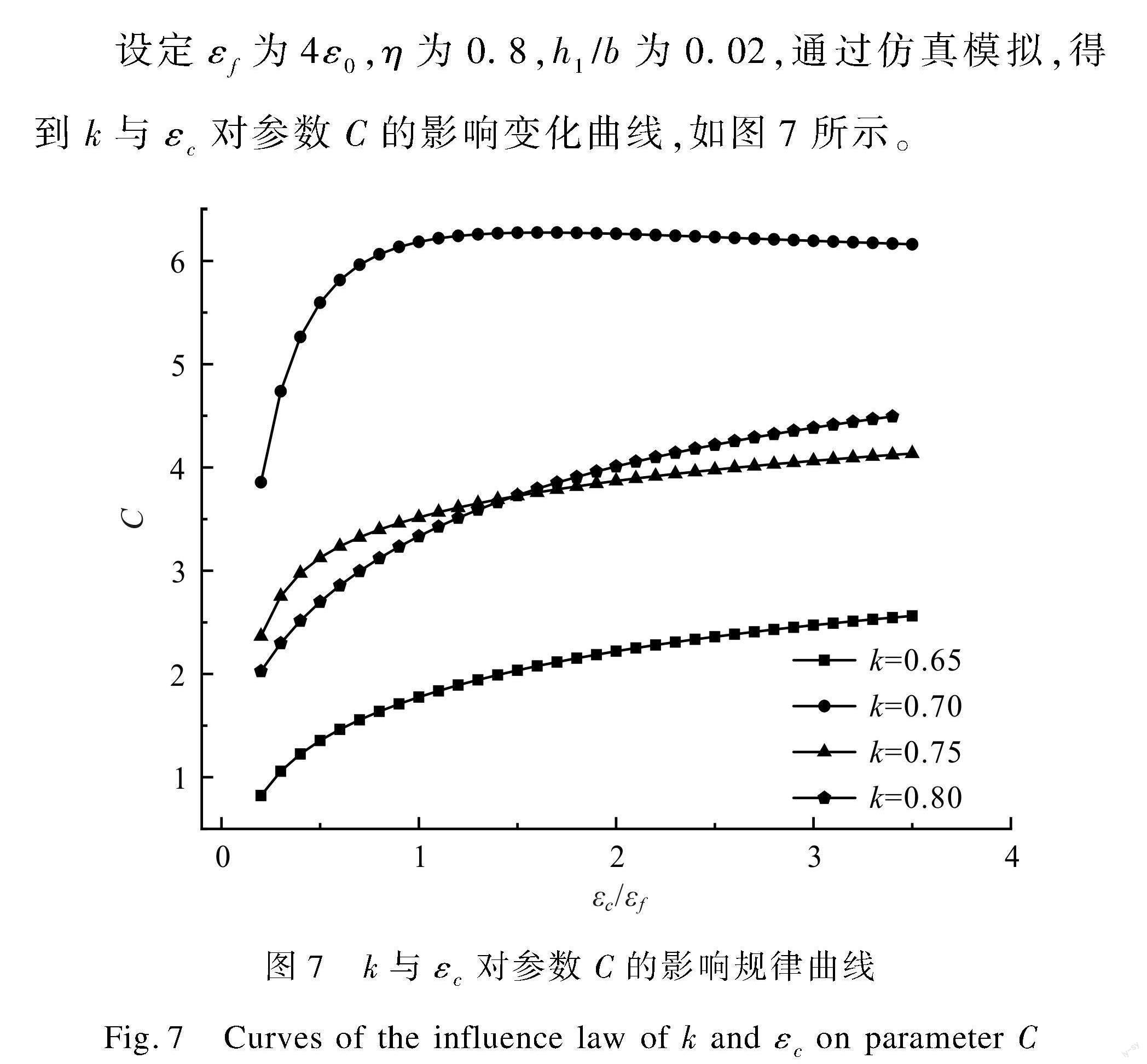
设定εf为4ε η为0. h1b为0.0 通过仿真模拟，得到k与εc对参数C的影响变化曲线，如图7所示。

由图7可知，电极占空比k一定时，参数C随绝缘介质层介电常数εc的增大而增大，静电吸附力也随之增大；当εc一定时，随着k的增加参数C呈现先增大后减小的趋势，表明静电吸附力与k并非呈现线性关系，而是存在最优值，大约在0.7。

2.3.4  极板间距t对吸附力F的影响分析

设定极板宽度2a=1 mm、η=0. 研究不同极板间距t（t=2（b－a））所对应单位长度织物上的吸附力F，结果如图8所示。由图8可知，静电吸附力随着电极间距t的增加呈现先增大后减小的趋势，当且仅当t为0.78 mm左右时，极板静电吸附性能最佳。

综上分析表明，静电吸附力与施加在电极上的电压平方成正比；织物密度越大，极板所产生的静电吸附力越大；随着绝缘介质层介电常数的增大，静电吸附力也相应增大；随着绝缘介质层厚度的增加，静电吸附力减小；随着极板占空比的增大，静电吸附力呈现先增大后减小的趋势；随着电极间距的增大，静电吸附力也呈现先增大后减小的趋势。

因此，静电极板的设计时应遵循：在保证接触高电压时，绝缘介质不被击穿且安全的前提下，尽量选用厚度较小、介电常数较高的绝缘介质；在设计电极时，电极间距与电极宽度之比应尽量保持在0.78左右。

3  结  论

本文针对纺织行业中服装面料抓取转移问题，提出采用静电吸附技术解决。首先，以纬编织物为研究对象，采用叉指状拓扑结构的双极型吸附电极作为吸附电极，通过构建理论与仿真静电吸附模型，验证了仿真模拟方法在静电吸附力分析方面的可行性。其次，建立了五层二维静电吸附力模型，利用Maxwell应力张量计算法系统性分析了吸附力模型结构参数对极板吸附性能的影响。最后，以提高极板单位面积吸附性能为目标，对静电吸附极板的结构参数进行了优化设计，并得出以下结论：

1）通过构建理论与仿真静电吸附模型验证了纬编织物结构在电场中确实受到静电吸附力的作用，同时证明了仿真模拟方法的有效性和可行性。

2）静电极板所产生的静电吸附力大小受到极板电压与极板结构参数的影响，通过改变极板电压和极板结构参数来提高极板的吸附性能。

3）静电极板的极板宽度与静电极板间距之间存在最优解，通过调整极板宽度和静电极板间距来提高静电极板整体的吸附性能。

本文结合理论构建、仿真模拟和优化设计等方面，研究结果可为后续静电吸附极板模型的设计和优化提供一定的理论参考。

参考文献：

［1］DOULGERI Z， FAHANTIDIS N. Picking up flexible pieces out of a bundle［J］. IEEE Robotics & Automation Magazine， 2002， 9（2）： 9-19.

［2］KAZEOONI H， FOLEY C. A robotic mechanism for grasping sacks［J］. IEEE Transactions on Automation Science & Engineering， 2005， 2（2）： 111-120.

［3］劉汉邦， 李新荣， 刘立东. 服装面料自动抓取转移方法的研究进展［J］. 纺织学报， 2021， 42（1）： 190-196.

LIU H B， LI X R， LIU L D. Research progress of automatic grabbing and transfer methods for garment fabrics ［J］. Journal of Textile Research， 2021， 42（1）： 190-196.

［4］KOLLURU R， VALAVANIS K P， HEBERT T M. A robotic gripper system for limp material manipulation： Modeling， analysis and performance evaluation［C］Proceedings of the IEEE International Conference on Robotics & Automation. Albuquerque： IEEE， 1997： 310-316.

［5］TAYLOR P M， MONKMAN G J， TAYLOR G E. Electrostatic grippers for fabric handling［C］Proceedings of the IEEE International Conference on Robotics & Automation. Philadelphia： IEEE， 1988： 431-433.

［6］PRAHALD H， PELRINE R， STANFORD S， et al. Electroadhesive robots： Wall climbing robots enabled by a novel， robust， and electrically controllable adhesion technology［C］2008 IEEE International Conference on Robotics and Automation. Pasadena： IEEE， 2008： 3028-3033.

［7］YAMAMOTO A， NAKASHIMA T， HIGUCHI T. Wall climbingme-chanisms using electrostatic attraction generated by flexible electrodes［C］2007 International Symposium on Micro-NanoMechatronics and Human Science. Nagoya： IEEE， 2007： 389-394.

［8］SOGARD M R， MIKKELSON A R， RAMASWAMY V， et al. Analysis of Coulomb and Johnsen-Rahbek electrostatic chuck performance in the presence of particles for extreme ultraviolet lithography［J］. Journal of MicroNanolithography， 2009， 8（4）： 2334-2343.

［9］BERENGUERES J， URAGO M， SAITO S， et al. Gecko inspired electrostatic chuck［C］Proceedings of the IEEE International Conference on Robotics and Biomimetics. Kunming： IEEE， 2006： 1018-1023.

［10］DHELIKA R， HEMTHAVY P， AKAHASHI K， et al. Compliant bipolar electrostatic gripper with micropillar electrodes array for manipulation at macroscale［J］. Smart Materials and Structures， 2016， 25（5）： 055037.

［11］GUO J C， DAI G H， CUI G C. A wall climbing robot based on the improved electro adhesion technology［J］. Applied Mechanics and Materials， 2013， 328： 56-61.

［12］王黎明， 胡青春. 基于静电吸附原理的双履带爬壁机器人设计［J］. 机械设计， 2012， 29（4）： 22-25.

WANG L M， HU Q C. Design of a double track wall-climbing robot based on the electrostatic adsorption mechanism［J］. Journal of Mechaine Design， 2012， 29（4）： 22-25.

［13］陈辉云. 基于静电吸附机理的机械抓手研究及设计［D］. 邯郸： 河北工程大学， 2018.

CHEN H Y. Research and Design of Mechanical Gripper Based on Electrostatic Adsorption Mechanism［D］. Handan： Hebei University of Engineering， 2018.

［14］劉立东， 李新荣， 刘汉邦， 等. 服装面料静电吸附抓取转移电极板优化设计［J］. 纺织学报， 2021， 42（2）： 185-192.

LIU L D， LI X R， LIU H B， et al. Optimization design of electrode plate based on electrostatic adsorption and transfer used for garment fabric［J］. Journal of Textile Research， 2021， 42（2）： 185-192.

［15］ABGHARY M J， HASANI H， NEDOUSHAN R J. Geometrical modeling for bi-axial weft knitted fabrics based on rib structure［J］. Indian Journal of Fibre & Textile Research， 2017， 42（4）： 431-438.

［16］张克和， 方园. 针织物结构研究与计算机仿真［J］. 浙江理工大学学报（自然科学版）， 2006， 23（1）： 8-12.

ZHANG K H， FANG Y. The study of knitting fabric structure and computer simulation［J］. Journal of Zhejiang Sci-Tech University（Natural Sciences）， 2006， 23（1）： 8-12.

［17］POURAZADY M， XU X. Direct manipulations of NURBS surfaces subjected to geometric constraints［J］. Computers & Graphics， 2006， 30（4）： 598-609.

［18］RUFFATTO D， PARNESS A， SPENKO M. Improving controllable adhesion on both rough and smooth surfaces with a hybrid electrostaticgecko-like adhesive［J］. Journal of the Royal Society Interface， 2014， 11（93）： 20131089.

［19］刘立东， 李新荣， 刘汉邦， 等. 基于纬编针织物特性的静电吸附力模型［J］. 纺织学报， 2021， 42（3）： 161-168.

LIU L D， LI X R， LIU H B， et al. Electrostatic adsorption model based on characteristics of weft knitted fabrics［J］. Journal of Textile Research， 2021， 42（3）： 161-168.

［20］CAO C Y， SUN X Y， FANG Y H， et al. Theoretical model and design of electroadhesive pad with interdigitated electrodes［J］. Materials & Design， 2016， 89： 485-491.

［21］YATSUZUKA K， HATAKEYAMA F. Fundamental characteristics of electrostatic wafer chuck with insulating sealant［J］. IEEE Transactions on Industry Applications， 2000， 36（2）： 510-516.

［22］HWANG G， PARK J， CORTES D S D， et al. Electroadhesion-based high-payload soft gripper with mechanically strengthened structure［J］. IEEE Transactions on Industrial Electronics， 2022， 69（1）： 642-651.

［23］FENG W Q， HU Y L， LI X R， et al. Robot end effector based on electrostatic adsorption for manipulating garment fabrics［J］. Textile Research Journal， 2022， 92（56）： 691-705.

［24］LIU Y， ZHAO X. Experimental studies on the dielectric behaviour of polyester woven fabrics［J］. Fibres & Textiles in Eastern Europe， 2016， 24（3）： 67-71.

Analysis of the effect of fabric and electrostatic pole plate parameters on the electrostatic adsorption force

WANG Qing， DANG Shuai， SHENG Xiaochao， L Xushan， JIANG Yuefu， ZHAO Tiantian

（School of Mechanical and Electrical Engineering， Xian Polytechnic University， Xian 710048， China）

Abstract：With the continuous advancement of textile and garment production processes， traditional fabric handling methods heavily reliant on manual labor are gradually insufficient for the demands of intelligent development. In addressing the issue of fabric handling， industrial robots currently employ various methods such as mechanical grasping， needle puncture， vacuum suction， and electrostatic adsorption. In comparison to traditional methods like mechanical arm gripping， needle puncture， or vacuum cup suction， electrostatic adsorption stands out as an ideal approach due to its stable adhesion force and high-precision gripping. Therefore， this paper opts for electrostatic adsorption technology to address the challenge of fabric handling in garment production. In the realm of electrostatic adsorption technology research， prior studies have predominantly focused on areas such as climbing robots and mechanical arms， with relatively limited systematic analysis in the field of fabric handling for garments. Building upon electrostatic adsorption technology， this paper delves into the transfer of garment fabrics， aiming to gain a profound understanding of the electrostatic adsorption force model. Through a systematic exploration of the impact patterns of fabric and electrostatic plate parameters on electrostatic adsorption force， the paper aims to provide a scientific foundation for the design and optimization of electrostatic plates.

To enhance the adhesion performance of electrostatic plates during the transfer of garment fabrics， this paper focused on warp-knitted fabrics， establishing a three-dimensional electrostatic adsorption model and a five-layer two-dimensional electrostatic adsorption model to provide scientific basis for the design and optimization of electrostatic plates. Firstly， the paper established a structural model for warp-knitted fabrics and a theoretical model for electrostatic adsorption force， ensuring the effectiveness of the research through theoretical analysis and simulation verification. Secondly， employing the Maxwell tensor method， the paper derived a five-layer two-dimensional theoretical model for electrostatic adsorption force， thoroughly investigating the impact patterns of internal structural parameters on adhesion force. Finally， through the optimization of structural parameters in the design of electrostatic adsorption plates， the paper aimed to enhance the adhesion performance of these plates， so as to provide theoretical support for the intelligent handling of garment fabrics. By introducing a five-layer two-dimensional electrostatic adsorption force model and employing the Maxwell stress tensor method for analysis， this paper extensively explored the impact of internal structural parameters on electrostatic adsorption force， offering a theoretical basis for more accurate predictions of electrostatic adsorption force. Simultaneously， the paper suggested the existence of optimal solutions for plate width and the distance between electrostatic plates， proposing adjustments to these parameters to enhance the overall adhesion performance of electrostatic plates.

Research findings indicate that by establishing a theoretical and simulation-based electrostatic adsorption model， the effect of electrostatic adsorption force on the warp-knitted fabric structure in an electric field is verified. The effectiveness and feasibility of the simulation method are confirmed. The magnitude of electrostatic adsorption force generated by the electrostatic plate is jointly influenced by plate voltage and plate structural parameters. Adjusting plate voltage and structural parameters enhances plate adhesion performance. Notably， in designing the electrostatic plate structure， an optimal proportion exists between plate width and the distance between electrostatic plates. Optimization suggests maintaining a ratio of around 0.78 between plate distance and electrode width to maximize overall electrostatic plate adhesion performance. Electrostatic adsorption technology injects new vitality into the textile and garment production industry， improving production efficiency by automating fabric handling and transfer processes. The introduction of this technology not only innovates the mode of production， but promotes the textile and garment industry to move towards a smarter and more efficient direction.

Key words：

fabric gripping; fabric modeling; fork-finger electrodes; electrostatic polar plates; electrostatic adsorption force; Maxwell