结合四元数拉盖尔矩和三维结构的图像哈希

白杰,赵琰

(上海电力大学电子与信息工程学院,上海 200090)

0 引言

随着网络媒体的日益发展,用户可以将更多的视频等包含大量图像的信息传入互联网。这些图像通过photoshop等图像处理软件进行一定操作就可以产生诸如改变亮度、添加水印、马赛克等拷贝版本。若有人恶意篡改图像则可能带来严重后果,因而正确区分这些图像至关重要。图像哈希技术的出现为这类问题带来了解决方法。图像哈希是指将一副图像定向映射为一串字符或数字序列。哈希算法需要具备具有鲁棒性、区别性、安全性、紧凑性等基本特性,在图像分类、检索等领域中被广泛应用。

1)基于变换的图像哈希。早期哈希主要通过图像变换来提取特征,如离散傅里叶变换(DFT)、离散余弦变换(DCT)、小波变换、对数极坐标变换等。文献[1]结合对数极坐标变换和离散傅里叶变换对图像提取旋转不变特征矩阵来构建哈希序列。文献[2]将DFT变换和Radon变换结合构建哈希,通过量化DFT变换系数和提取变换后的特征得到哈希。以上两种算法在对抗攻击的鲁棒性方面效果有限,且适用攻击操作种类较少。文献[3]考虑到对数极坐标变换具有良好的旋转不变性,结合LT变换和四元数傅里叶变换,将经过LT变换的次级图像提取QDFT幅度矩阵完成哈希算法,该算法鲁棒性较强但可对抗操作不多。文献[4]将图像进行非重叠分割,提取每个图像块的DCT系数并量化得到鲁棒的哈希序列。基于同样的非重叠分割思想,文献[5]使用canny算子计算图像块的特征点,选取代表性强的特征块和位置信息与DCT系数连接,经过主成分分析(PCA)得到哈希序列,这两种算法可对抗的攻击操作种类有所增加,但旋转攻击抗性都较弱。文献[6]使用Radon变换提取图像系数并进行一维DCT,通过低频系数统计特征得到哈希序列,该算法的旋转抗性较优。文献[7]利用多级离散小波变换(DWT)提取特征构造哈希序列。文献[8]在小波变换基础上结合图像的特征点构造哈希序列,增强了算法的区别性。文献[9]提出将对数极坐标变换和Gabor变换相结合提取图像特征,该算法在区分性良好的基础上还具有较强的紧凑性。早期的图像哈希算法结构较为简单,主要聚焦于提高算法的鲁棒性和区别性,但对计算效率、攻击容量有所欠缺。因此,在保证算法鲁棒性的前提下,为了提高算法的处理效率,序列紧凑性也成为优化的目标。

2)基于数据降维的图像哈希。文献[10]将局部线性嵌入用于哈希序列的压缩,降低了算法的计算代价。随后文献[11]提出使用图像的最大内接圆进行等面积环形分割将图像重组为列,再进行非负矩阵分解提取特征,该算法对旋转攻击的鲁棒性良好,但由于使用环分割导致图像边缘处的敏感性不足。文献[12]提取图像块纹理特征并压缩。文献[13]将小波分解和CS-LBP相结合,该算法性能良好,且具备了一定的拷贝检测能力。文献[14]提出利用WeberLBP提取图像的纹理特征,并与图像的颜色特征相结合构建哈希算法,使用PCA压缩数据使得算法具有不错的紧凑性。文献[15]在Lab颜色空间中结合环形分区和向量不变矩,提出了具备区别性和强鲁棒性的算法。

3)基于颜色特征和图像矩的图像哈希。随着研究的深入,简单的变换方式和单一的特征构成已经不能满足对算法性能的要求。文献[16]将RGB彩色图像转换到HSI和YCbCr颜色空间,计算各分量均值和方差,提取局部颜色特征。文献[17]以图像颜色特征作为出发点,提取彩色图像的对立色并分块提取颜色特征,再对亮度图像进行四叉树分解得到结构特征,联合两种特征组成哈希序列。该算法具有强鲁棒性并且可以进行篡改定位。文献[18]使用图像的Zernike矩构成哈希序列,结合保角变换,提取图像的角信息,提高算法鲁棒性且可以进行篡改定位。

此外,文献[19]利用四元数奇异值分解计算出拼接图像的噪声信息,增强了图像的特征表达。文献[20]使用空洞卷积提取不同尺度的图像特征,将多尺度特征融合后作为网络的输入,有效增强了算法的检测性能。这些针对图像特征的提取和表达方面的改进值得学习借鉴。

目前的哈希算法在保证鲁棒性的前提下各具优势,但仍存在一些短板,如针对灰度图像的方案整体鲁棒性较强但不适用于彩色图像,可对抗的攻击种类较少。本文提出一种可以直接处理彩色图像并且在鲁棒性、区别性和序列紧凑性上具备一定优势的算法。由于拉盖尔矩对多数篡改操作具有鲁棒性,将其与四元数理论相结合拓展到图像哈希中,直接提取RGB图像的特征,得到的全局特征具有较好的鲁棒性。对预处理后的图像提取能量,在三维空间视角下提取能量的结构特征,在保证算法鲁棒性的同时提高区别性,增强对旋转攻击的鲁棒性。

1 本文图像哈希算法

1.1 算法框架

图1是结合四元数拉盖尔矩和三维结构特征的哈希算法流程,主要由预处理、特征提取、哈希生成组成(彩色效果见《计算机工程》官网HTML版,下同)。图像预处理是指对图像进行双线性插值得到二次图像,再对二次图像进行多尺度融合分别得到高斯融合图像和拉普拉斯融合图像。特征提取包括全局特征和三维能量结构特征,全局特征是指提取图像的四元数拉盖尔矩系数,三维能量结构特征是指利用亮度图像的能量和非重叠分割后各子块的能量,在三维空间下提取结构特征。哈希生成将所得各部分特征量化组合得到中间哈希,经过密钥加密生成哈希序列。

图1 哈希算法流程Fig.1 Procedure of Hash algorithm

1.2 图像预处理

用双线性插值统一输入图像尺寸为N×N,以处理不同大小的输入图像。该操作可以略微提升缩放攻击抗性,对统一尺寸图像I0进行下采样。下采样的模糊图像记为I1、I2、I3、I4。再用圆盘均值滤波器进行多级滤波。拉普拉斯金字塔表达式如式(1)所示:

(1)

图像金字塔包含不同尺度下图像的信息。I0、I1、I2、I3为四级高斯金字塔,L1、L2、L3、L4为四级拉普拉斯金字塔,将图像金字塔进行融合可以发挥增强图像的作用。通过多尺度融合得到二次图像的高斯融合图像IM和拉普拉斯融合图像LM,如式(2)所示:

(2)

1.3 全局特征提取

文献[21]提出在笛卡儿坐标系中灰度图像的广义拉盖尔矩,广义拉盖尔多项式可以由式(3)定义:

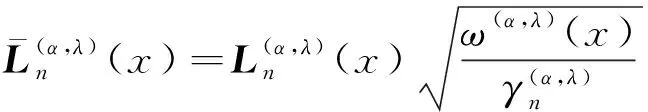
(3)

由式(3)可得,广义拉盖尔矩的定义如式(4)所示:

(4)

其中:fgray(i,j)表示一幅N×N的灰度图像。

(5)

表1 Ln,m系数Table 1 Ln,mcoefficients

由于两种融合图像求得的四元数拉盖尔矩系数是复数形式,因此对其求模并排列为行向量,则IM的四元数拉盖尔矩系数为G= [g1,g2,…,gn(n+1)/2],LM的四元数拉盖尔矩系数为J= [j1,j2,…,jn(n+1)/2]。按式(6)分别对融合图像的矩系数进行二值化,GM和JM为G和J的均值,G1和J1为二值化向量,i= 1,2,…,n(n+1)/2。

(6)

连接融合图像的矩系数得到全局特征HQ=[G1,J1],长度为L1=n(n+1)。

1.4 三维能量结构特征提取

文献[22]提出图像在经过常见的攻击操作前后,其能量并不会发生大的波动,所以可以认为图像能量对于常见攻击操作有较好的鲁棒性。算法在YCbCr颜色空间下提取高斯融合图像的亮度图像Y,对于尺寸为N×N的亮度图像,它的能量E可以表示为:

(7)

其中:trace(·)表示矩阵的迹;yi,j表示亮度图像Y的像素值。本文选择在三维空间内进行特征提取,图像的三维能量结构特征由两部分组成。第一部分先计算亮度图像Y的能量矩阵NE,以NE的行位置为x轴、列位置为y轴、能量值为z轴构建三维模型,在xOz和yOz两个投影面上画出峰顶曲线和峰谷曲线,求取峰值点与谷值点连线的夹角余弦值。第二部分以b×b的子块大小非重叠分割亮度图像,计算各子块能量值得到亮度图像的分块能量矩阵NY,以NY的行位置为x轴、列位置为y轴、能量值为z轴构建三维模型并画出等高线,求出特定点到等高线上最近点和最远点连线的余弦值,从而充分提取三维结构特征。

本文算法三维特征在构造时主要考虑:1)使用图像能量构造三维模型;2)通过提取峰谷值点和分重叠分割使哈希序列更紧凑;3)加入等高线特征增强抵抗旋转攻击的能力。

三维能量图像和相应投影面的峰谷值曲线如图2所示。

图2 三维能量模型和峰谷值曲线Fig.2 Three-dimensional energy model and peak and valley value curves

按照式(8)获得NE在xOz投影面下的峰顶曲线M1和峰谷曲线M2,同理可以得到NE在yOz投影面下的峰顶曲线M3和峰谷曲线M4。

M1=max(NE,1),M2=min(NE,1)

(8)

其中:min(·,1)和max(·,1)表示按行取NE最小值和最大值。在不同投影面的峰谷值曲线上等间距取出16对峰谷值点,记xOz投影面取出的峰值点集为M1P,谷值点集为M2V,yOz投影面取出的峰值点集为M3P,谷值点集为M4V。提取xOz投影面峰值点集M1P在xOy平面上的位置信息矩阵P=[P1,P2,…,P16]与yOz投影面峰值点集M3P在xOy平面上的位置信息矩阵U=[U1,U2,…,U16]。同理,xOz投影面谷值点集M2V在xOy平面上的位置信息矩阵Q=[Q1,Q2,…,Q16],yOz投影面谷值点集M4V在xOy平面上的位置信息矩阵V=[V1,V2,…,V16]。将xOz投影面上的峰值点集按照序数从大到小依次与谷值点集序数从小到大的顺序相连,形成线段集S=[P1Q16,P2Q15,…,P16Q1],共计16条线段。同理,取得yOz投影面上的峰值点与谷值点的线段集K=[U1V16,U2V15,…,U16V1]。记xOy平面为F,求出这些线段与xOy平面夹角的余弦值,将一系列余弦值排列成行向量并按式(9)进行二值化。

(9)

其中:SM表示xOz平面线段集与水平面F夹角余弦值的平均值;KM表示yOz平面线段集与水平面F夹角余弦值的平均值,i=1,2,…,16;H1、H2长度都为16。以上是通过图像在三维能量模型上不同投影面的特征点得到局部结构特征。

为了进一步提高算法对于旋转攻击的鲁棒性,接下来对图像进行抗旋转特征提取。使用图像子块能量值作为等高线特征的z轴主要原因如下:1)图像子块的能量值对常见的攻击操作同样具有良好的鲁棒性;2)分块处理可以在不影响算法鲁棒性的前提下有效降低数据维度,提高计算效率;3)为了提高对于旋转攻击的鲁棒性,选择在三维结构上寻找等高线提取抗旋转的结构特征,图像分块处理可以使算法以微弱降低ROC曲线表现力为代价,明显提升对旋转攻击的鲁棒性。具体步骤如下:算法利用亮度图像的分块能量矩阵NY的信息,以行位置信息为x轴、列位置信息为y轴、子块能量值为z轴构造三维模型。在三维结构上画出一系列等高线,选定xOy平面的中心点O作为原点,找到原点在每一条等高线上距离最近和最远的两点。这样做的优点是当图像受到任意角度的旋转攻击,分块能量矩阵的三维模型会随之发生旋转,但等高线只会发生水平旋转,所选取的原点到等高线上任意一点的连线与水平面的夹角在旋转前后不会发生改变。所以选取这样一组在任意角度旋转攻击下保持不变的特征有助于提高算法的鲁棒性。分块能量矩阵NY的三维模型等高线和等高线在xOy平面的投影示意图如图3所示。

图3 等高线模型示意图Fig.3 Schematic diagram of the contour model

为便于观察,图3显示了取4条等高线的三维结构示意图,且标注出了中心点O所在位置。求解原点到等高线近点远点连线与水平面F的余弦值,记为近点余弦值集Dmin=[D1,D2,…,Dn],远点余弦值集Dmax=[d1,d2,…,dn],将其按式(10)进行二值化:

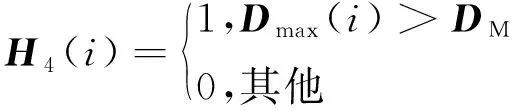
(10)

其中:DM为所有连线与水平面夹角余弦值的平均值;i=1,2,…,n;H3、H4长度都为n。通过联合投影面峰谷值点的局部结构特征和分块能量矩阵的等高线特征,得到图像的三维能量结构特征HE=[H1,H2,H3,H4],L2=2n+32表示HE的长度。

1.5 哈希生成

连接HQ和HE得到中间哈希Hmid=[HQ,HE],本文算法得到的哈希序列长度为L=L1+L2=n(n+1)+2n+32。出于安全性考虑,用随机生成的1 000个伪随机数列w重排中间哈希Hmid得到最终哈希序列h,如式(11)所示:

h(i)=Hmid(w[i])

(11)

其中:w(i)表示伪随机数序列w的第i个数。本文算法得到二进制哈希序列,选择汉明距离作为图像相似度判断依据,当两幅图像的汉明距离小于阈值T时判断为相似图像,反之为不同图像。汉明距离D的计算公式如式(12)所示:

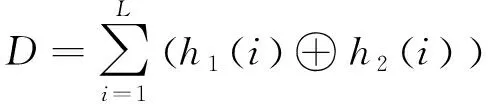
(12)

其中:h1(i)和h2(i)是h中的第i个元素;⨁为异或运算;h1、h2表示进行判断的两幅图像。

2 实验结果与分析

本节主要进行包括鲁棒性实验、区别性实验、参数分析、不同算法对比。实验中使用的参数如下:图像归一化尺寸N=256,图像子块大小b=16,阶数n=8,故算法的哈希序列长度为L=120 bit。所有的实验均通过MATLABR2019a平台进行仿真。

2.1 鲁棒性实验

鲁棒性实验中测试样本由图4所示的20幅彩色图像组成。

图4 鲁棒性实验图像Fig.4 Images of robustness experiments

按照如表2所示的操作攻击每幅测试图像,单个测试图有66个相似版本,将测试图像与相似图像配对,计算相似图像对的哈希距离。

表2 鲁棒性实验攻击参数Table 2 Attack parameters for robustness experiments

表3是20幅测试图像经过以上12类攻击操作得到的相似图像与原图像的哈希距离统计。由表3可以看出,相似图像与原图像的哈希距离都落在0～18区间内,哈希距离均值都不超过12。说明本文算法对常见的攻击操作具有良好的鲁棒性,并且当阈值设置到18以上时,理论上可以将全部的相似图像识别出来。

表3 哈希距离表Table 3 Hash distance table

图5展示了图4中前5个测试样本在不同篡改攻击下的哈希距离分布,可得算法对多种常见攻击的鲁棒性都较好。

图5 鲁棒性实验结果Fig.5 Results of robustness experiments

2.2 区别性实验

表4 区别性实验攻击参数Table 4 Attack parameters of the differentiation experiment

图6展示了不同图像对和相似图像对的哈希距离分布。其中,横坐标表示汉明距离,纵坐标表示该距离下相似或不同图像对数目。由图6可以看出,相似图像对汉明距离区间为0～45,不同图像对汉明距离区间为22～118,即在汉明距离为22～45时,相似图像对和不同图像对发生了重叠。算法选取碰撞率(PC)和检错率(PE)指标衡量区别性,根据式(13)计算确定合适的阈值区分相似和不同图像对。

图6 汉明距离分布Fig.6 Hamming distance distribution

PC=NC/ND

PE=NE/NS

(13)

其中:NC表示不同图像误判相似图像数;ND为不同图像数;NE表示相似图像误判不同图像数;NS为相似图像数。计算结果如表5所示,由图6和表5可知,当阈值T=34时,碰撞率为7.80×10-5,检错率为2.42×10-5,综合考虑碰撞率和检错率,选择T=34为阈值。

表5 各阈值检错率和碰撞率Table 5 Error detection rate and collision rate for each thresholds

2.3 参数分析

2.3.1 阶数n和分块大小b对算法的影响

实验在除阶数和分块大小以外的条件固定情况下,取n=[6,7,8,9],b=[8,16],两两组合分别进行实验。通过ROC[25]曲线衡量选取阶数和分块大小的不同取值时算法的综合性能如图7所示。参数分析实验的数据集与前文区别性实验相同。通过错误接受率(PFPR)和正确接受率(PTPR)指标衡量区别性,计算公式如式(14)所示:

图7 各分块大小和阶数下的ROC曲线Fig.7 ROC curves for each block size and order

PFPR=n1/N1

PTPR=n2/N2

(14)

其中:n1指错判相似图像对数;n2为正确判定相似图像对数;N1和N2分别为不同图像对和相似图像对的总数。

图7显示,当n=8、b=16时,算法的ROC曲线表现力最佳,且当b的取值固定为8或16时,曲线表现力都随着n由6增加到8持续提高,但n=9时哈希序列长度达到140,等高线特征长度达到18,一定程度上影响了算法的综合表现力,故综合考虑当n=8、b=16时为最佳选择。

2.3.2 多尺度融合处理的效果

由于所提算法在预处理的过程中为了强化对图像信息的表达,对插值以后的二次图像进行了多尺度融合的处理,因此在所有参数都相同的情况下,将经过多尺度融合的算法和直接使用二次图像进行特征提取并计算哈希的算法进行比较。ROC曲线对比如图8所示,说明算法经过多尺度融合后,区别性有所提高。

图8 多尺度融合前后的ROC曲线Fig.8 ROC curves before and after multi-scale fusion

2.3.3 等高线特征对旋转抗性的影响

为了验证等高线特征对算法在旋转攻击鲁棒性方面的影响,在其他参数相同的情况下,不添加等高线特征的算法对旋转攻击的鲁棒性和加入等高线特征的旋转攻击鲁棒性如图9所示。

图9 加入等高线特征前后的鲁棒性对比Fig.9 Robustness comparison before and after adding contour features

图9(a)是无等高线特征的旋转攻击鲁棒性图,哈希序列长度为104,可以看出,在0.2°～1.0°的旋转攻击下,哈希距离最高为22,且上升趋势明显。图9(b)为加入等高线特征的旋转攻击鲁棒性,哈希序列长度为120,由图9(b)显示在0.2°～1.0°的旋转攻击下,哈希距离最大为14,图9(c)显示在1.0°～5.0°旋转攻击下,哈希距离最大为26。可以看出,在哈希序列长度增加的同时,原始图像与经过旋转攻击的图像之间的哈希距离反而有所降低,证明等高线特征的加入有效提高了算法对于旋转攻击的鲁棒性和综合表现力。

2.4 图像分类性能对比

为考量本文算法的图像分类性能,将本文算法与文献[12,26-28]算法的ROC曲线性能进行对比。为保证公平性,本节参与对比的各个算法使用同样的数据集并且在相同平台运行。图10展示了不同算法之间ROC曲线对比。

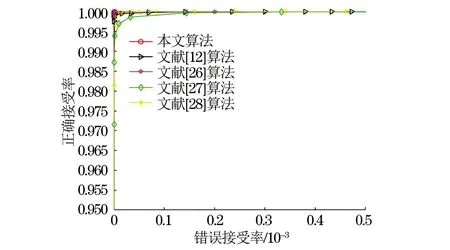
图10 不同算法的ROC曲线对比Fig.10 ROC curve comparison of different algorithms

当PFPR=0时,本文算法的PTPR为0.999 2。参与对比的算法[12, 26-28]PTPR分别为0.998 5、0.999 1、0.924 5和0.996 4。当PTPR接近于1时,本文算法的PFPR为0.000 6,文献[12, 26-28]算法的PFPR分别为0.112 1、0.002 0、0.761 1和0.060 4。可以看出,当PFPR=0、PTPR=1时,本文算法的表现都优于对比算法。在算法的哈希生成效率和储存代价方面,计算了同样外部参数情况下本文算法与各对比算法的总运行时间和哈希长度。将1 000张输入图像产生哈希序列的总时间记录下来并除以1 000得到各个算法的平均哈希生成时间。表6综合记录了本文算法与对比算法的性能对比。通过表6可以看出,本文算法的哈希序列长度为120 bit,在所有对比算法中紧凑性最好,运算速度快。图10展示出本文算法的ROC曲线最接近图像的左上角,说明本文算法的综合性能较好。

表6 不同算法的性能对比Table 6 Performance comparison of different algorithms

由于等高线特征通过分块能量矩阵得到,若图像归一化尺寸N发生变化,等高线特征就会随之变化而改变算法性能。为了展现本文算法在不同N值下的性能,选择N=256和N=512,通过ROC曲线来衡量算法性能,如图11所示。可以看出,本算法在N=512时性能发生了轻微下滑,这是由于虽然N取值的变化会使图像的分块能量矩阵发生变化,但等高线特征的长度并不会受到影响,从而将归一化尺寸波动带来的影响控制在可接受的范围内。文献[12]算法性能下滑非常明显,这是由于N取值提高导致哈希序列过长,在区别性上的表现下降明显,从而影响了ROC曲线。文献[26]算法也有一定程度的削弱。由图易得,在N=256时本算法具有ROC曲线表现上的优势。

图11 各算法在不同N值下ROC曲线对比Fig.11 Comparison of ROC curve of each algorithms under different N values

2.5 拷贝检测实验

图像检索在实际应用中面对的目标应该是互联网媒体中的各种图像,但在实验研究中通常使用已有的数据库,并对这些数据库中的图像进行攻击处理来验证算法的图像分类性能。拷贝检测实验则是在网络上随机下载图像,并对图像进行攻击处理。原始图像的来源不同可能导致分辨率、尺寸、颜色空间上的差异。这些差异在实验中会体现为算法可能在对某些数据库上能表现出较好的图像分类性能,但在拷贝检测实验中表现会有所降低。引入文献[29]提出的查全率(P)和查准率(R)作为衡量算法在拷贝检测方面性能的指标。随机下载1 000幅网络图像为拷贝检测原始图像库,其中抽取100幅作为查询图像库。对查询图像库的图片进行28种攻击操作,如表7所示。将得到的拷贝图像和原始图像库共计3 800幅作为实验图像库,对查询图像库进行实验。P和R的计算公式如式(15)所示:

表7 拷贝检测攻击参数Table 7 Attack parameters for copy detection

P=N3/N4

R=N3/N5

(15)

其中:N3是结果中正确查询拷贝图像数;N4是结果中拷贝图像数;N5是测试图像库中拷贝图像数。

表8是进行5次随机抽取后,拷贝图像与查询图像之间汉明距离在选择不同的阈值下算法的平均查全率和查准率。当得到的汉明距离小于所选阈值时,认为该图像为拷贝图像,反之则认为图像是实验数据库中除拷贝图像之外的其他图像。由表8可以看出,当阈值为30时,算法能以94.92%的准确率将所有拷贝图像识别出来;当阈值取38时,查全率为97.58%,查准率为96.77%。

表8 平均查全率和查准率Table 8 Average completion rate and accuracy rate

同时为了增强查全率与查准率指标的稳定性,选取1 000幅图像中的400幅进行多次随机抽取实验得到的平均查全率与查准率如表9所示。

表9 增加查询图像后的平均查全率和查准率Table 9 Increase the average search completion rate and accuracy rate after querying images

通过拷贝检测实验与文献[12,22,26-27]算法进行比较,画出查全率和查准率曲线,结果如图12所示。可以看出,本文算法P-R曲线最靠近右上角,优于其他算法。结果表明,本文算法在拷贝检测应用方面具有较好的表现。

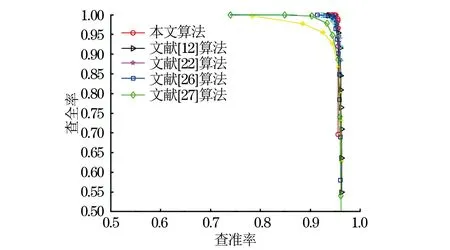
图12 不同算法的P-R曲线对比Fig.12 Comparison of P-R curve of different algorithms

3 结束语

本文提出一种结合四元数拉盖尔矩和三维能量结构的哈希算法。用四元数拉盖尔矩提取融合彩色图像的全局特征,对三维空间下高斯融和图像的能量信息建立模型并提取结构特征,同时对非重叠分割后的能量信息构建三维模型,提取其中抗旋转的等高线特征,提高鲁棒性。实验结果表明,该算法的哈希长度紧凑,运算速度快,鲁棒性与区别性之间取得了较好的平衡。下一步将尝试对等高线特征进行拓展,使算法在保证性能的前提下增强对更大角度旋转攻击的鲁棒性。