移动边缘网络中的多目标缓存优化方法
吴 越,薛钊煜,郭婉婉,崔志华
(太原科技大学 计算机科学与技术学院,太原 030024)
0 引 言
随着信息技术的快速发展,各种社交媒体、视频网站的发展十分迅速,用户量快速增长,大量的网络通信流量对基站造成了巨大的压力.基于移动边缘计算(MEC)的缓存方法利用边缘网络靠近用户的特点和感知与存储能力,将数据放置于靠近用户的边缘节点上,能够有效降低网络负载、提升服务质量.但是在边缘网络环境中,每个边缘节点的可用缓存空间十分有限,因此如何合理的利用有限的缓存空间将流行度更高的内容放置于合适的位置成为了关键问题.
为了提高MEC缓存的性能,研究人员做出了许多工作.文献[1,2]使用基于贝叶斯的流行内容预测来制定缓存预取方案;文献[3]将存储资源和计算资源推到网络边缘,基于长短期记忆(LSTM)神经网络预测内容流行度,将预测结果应用于缓存方案的制定;文献[4]基于博弈论的思想将边缘网络中的节点看做博弈者,决定自身的缓存策略来达到最大缓存收益,在博弈中达到纳什均衡并据此设计了一种分布式均衡算法;文献[5]基于多臂强盗方法设计的解决如何估计未知用户偏好,并提出了一种基于多智能体扩展单抗的解决方案,实现了分散的缓存放置策略;文献[6]使用神经网络模型预测未来可能的用户请求,并通过联合优化延迟和能耗来制定缓存方案;文献[7]使用Zipf定律估计用户偏好,将目标建模为延迟最优,提出了基于改进KM(Kuhn-Munkres)的内容放置方法;文献[8]从服务运营商的角度将数据缓存问题表述为一个约束优化问题,优化目标位延迟最低,用整数规划的方法来解决优化问题;文献[9]结合了基于长短期记忆(LSTM)的局部学习和基于集成的元学习来提高预测性能继而提高缓存命中率.以上研究主要针对估计用户偏好,根据估计的用户偏好进行缓存决策,虽然能够提高缓存性能,但考虑缓存问题的角度单一,不能满足多样化的缓存需求.
针对复杂的缓存需求,文献[10]将RAN建模为一个区域,通过划分区域的方式简化问题,将缓存问题表述为一个混合整数线性规划模型,文献[11]同样使用区域划分的方式建模,提出基于博弈论的缓存放置策略;文献[12,13]从服务提供商的角度考虑,在满足访问延迟约束的前提下最大化服务提供商的利益;文献[14-16]使用数据访问计数、数据访问频率和数据大小作为优化目标的多目标优化数据缓存模型,结合了蚁群算法和遗传算法进行求解;文献[17]为了克服缓存污染问题,提出了LRU-GENACO,该方法结合了LRU、ACO和GA算法,其中LRU算法被分配用于解决缓存污染问题,而混合ACO-GA在缓存数据被消除之前优化缓存数据选择;[18]使用评估的缓存值、数据对象获取和替换成本将缓存放置问题建模,使用禁忌搜索算法求解模型;文献[19]提出了一种基于贪心算法的云边缘协同缓存模型和相应算法,以降低负载提高缓存命中率;文献[20]提出了归一化布谷鸟搜索算法联合优化延迟、功耗、连接成功率;文献[21]基于博弈论的思想研究了联合优化中如何公平的处理具有竞争关系的优化目标,将QoE和能量效率作为博弈对象,置于纳什均衡模型中,并提出了一个公平的多回合博弈算法;文献[22]提出了一种基于多臂强化学习的实用感知协作服务缓(UACSC)方案,以协调多个边缘服务器以做出动态联合缓存决策,在最小化缓存成本的同时优化服务延迟.文献[23]将STP和平均传输延迟建模为一个多目标优化问题,以最大化STP或最小化延迟为目标,并建立了多目标缓存布局优化问题.提出了一种新的投影多目标杜鹃搜索算法(PMOCSA),以获得最优缓存布局的解决方案.上述研究考虑了多样化的缓存需求,大部分通过将多目标转化为单目标的方式联合优化,然而多个目标之间的关系难以区分、不易比较,不同目标的权重参数确定方式十分主观,尤其是目标之间互相冲突时会使加权目标函数的结构十分复杂,权重参数需要在优化开始前确定,在迭代过程中无法干预,这使得优化结果难以使人满意.
综上本文站在不同的角度观察MEC缓存方案得到了不同的需求[24]:用户希望能在更短的时间内得到响应获得所访问的内容;网络提供商希望使得边缘节点的负载尽可能地低,缓存效率更高;服务提供商则希望降低缓存成本的支出.为了使多个利益相关方均能收益,提升系统整体性能,本文构建了一个考虑3个目标的边缘缓存模型,并设计了一种基于最远交配和淘汰策略的多目标进化算法(MOEA-FMES).
本文的重要贡献总结如下:
1)构建了一个考虑用户时延、缓存存储成本和边缘节点传输能耗的多目标缓存模型,以提高系统的整体性能,使得不同的利益相关方均能从中收益.
2)为了求解所提出的缓存模型,设计了MOEA-FMES,采用基于参考向量的最远距离选择来选择父代个体;采用一种基于BDE和欧式距离的动态适应度值算子;在环境选择中循环淘汰机制选出下一代种群.
3)为了验证所提方法的有效性、评估提出算法,设计了模拟仿真试验,通过对比AGEII、IBEA、SPEA/R、NSGAII、VaEA和MOEA-FMES说明了本文提出方法的有效性.
1 模型设计
1.1 网络模型
边缘云计算环境是多层网络架构,包括云计算层、边缘计算层和终端层.为了能够更为高效的利用边缘网络资源来提升服务效率,需要将高流行度的缓存内容放置在合适的边缘节点.不同的放置方案会产生不同的影响、收益,如前文所述,MEC缓存中的利益相关方之间互相冲突.
本文考虑如图1所示的网络架构,包含一个宏基站(MBS)和M个小基站(SBS),宏基站通过光纤链路与云网络连接,通过BS链路与SBS连接;每个SBS与不等数量的用户设备(UE)连接,MBS中存储整个内容库,考虑到实际情况中的内容大小不同,本文假设内容库包含N个大小不等的内容,记为D={d1,d2,…,dN},内容大小服从参数为α的正态分布.使用E={e1,e2,…,eM}表示SBS集合,SBS的存储容量有限,容量大小记为C.将用户连接的SBS称为本地SBS,当UE所请求的内容不在本地SBS中时,可以向一跳友邻SBS请求内容,若一跳友邻SBS也没有缓存内容时,向MBS请求内容,SBS之间的关联情况由Z={zm1,zm2,…,zMM}表示,zmm=1表示互相连接,否则表示不连接,Y={y1,y2,…,yN}表示SBS连接的用户的数量的集合,本文假设在时隙t内Y服从参数为δ的泊松分布.X={xm1,xm2,…,xmn}表示缓存方案,xmn表示基站em是否缓存内容dn,1表示缓存该内容,0则表示不缓存该内容.
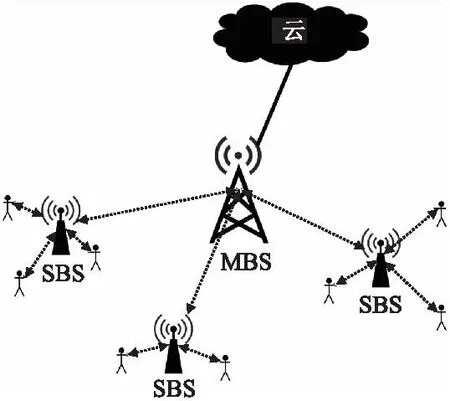
图1 MEC结构Fig.1 MEC structure
1.2 缓存模型
本文考虑在时隙t内的缓存内容放置方案,假设在时隙t内内容的流行度基本稳定不变.齐普夫(Zipf)定律被用于估计内容的流行度已经被证明了其有效性,许多的研究也基于假设满足该定律展开,如文献[25]证明YouTube上的内容流行度服从Zipf分布.因此本文假设内容流行度服从Zipf分布.内容库中包含N个内容,并按照访问次数进行降序排序P={p1,p2,…,pN},表示内容的请求概率分布,pi表示第i个内容被请求概率,概率值由公式(1)按照Zipf计算:
(1)
式中γ为参数控制分布的密集程度.
SBS、MBS向所连接的设备发送数据的速率V由公式(2)得出:
(2)
式中y表示所连接的设备数量,B为带宽,Q为平均发射功率,μ为噪声功率.SBS的缓存空间大小记为C.
1.3 优化目标
本文针对MEC缓存中不同利益方的需求,提出了3个优化目标,分别为延迟、缓存成本、基站传输功耗.当用户请求的内容不在本地SBS时,仅向一跳友邻SBS或MBS发起请求.因此本文中所计算的延迟、传输功耗需要综合考虑不同的情况进行计算,即a)请求的内容缓存于本地SBS时,直接向用户返回内容;b)请求的内容未缓存与本地SBS但缓存于友邻SBS时,首先将请求的内容发送至本地SBS,再由本地SBS发送给用户;c)当请求的内容本地SBS与友邻SBS均未缓存时,先由MBS发送至本地SBS,再由本地SBS发送给用户.delay(m)表示某个SBS所连接用户的延迟,计算方式由公式(3)给出.cost(m)表示某个SBS所缓存的内容大小,用于衡量缓存成本计算方式由公式(4)给出,用于衡量存储成本,power(m)表示某个SBS提供服务时的传输功耗,计算方式由公式(5)给出.
delay(m)=t1+t2+t3
(3)
(4)
power(m)=Qst1+Qst2+QMt3
(5)
其中t1为情况a下的延迟;t2为情况b下的延迟;t3为情况c下的延迟.
(6)
(7)
(8)
式中BS,BM分别表示SBS和MBS的带宽,QM,QS分别表示SBS和MBS的平均发射功率.
那么可以得到3个互相冲突的目标,分别是:用户平均延迟f1,SBS平均缓存成本f2,平均传输功耗f3.由于本文考虑的SBS的缓存空间大小有限且一致,故每个SBS所缓存的内容大小必须不大于C.
因此MEC缓存多目标优化问题可以表述为:
(9)
显然的,延迟与缓存是否命中相关,节点缓存的内容越多缓存命中的可能性越高将会使得平均延迟越低,而这将导致缓存成本变高,所以f1与f2互相是冲突的.另外当缓存命中时本地SBS直接向服务的用户发送数据,而未命中时则需要友邻SBS或MBS先向本地SBS发送数据再由本地SBS发送给服务的用户,所以节点缓存内容增加将使得平均传输功耗降低,故而f2与f3互相冲突.由于MBS发射功率高于SBS,因此当友邻节点缓存了本地所请求的内容时本地SBS无需向MBS请求数据从而降低了功耗但相应的提高了延迟,因此f1与f3也是互相冲突的.图2(a)~图2(c)展示了求解本文时模型不同目标值之间的关系,通过观察图中解的分布也能得出相同的结论.

图2 目标值关系图Fig.2 Objective value relation diagram
2 算法改进
上述问题是一个非凸优化问题,进化算法是解决大规模非凸优化问题的一种有效方法.再过去的十数年中,研究者们提出了多种高性能多目标进化算法.这些算法的基本一般过程是:1)随机生成初始种群并计算目标函数的值;2)通过交配选择算子从种群中选择个体,以杂交和突变产生后代种群;3)父代和子代种群被合并,下一代种群从环境选择算子中选择;4)重复上述操作,直到满足终止条件.其中,匹配选择算子和环境选择算子极大地影响了算法的求解性能.为了更好地平衡分集和收敛,本文提出了MOEA-FMES算法,在匹配选择时采取最远邻居结合的策略来增加多样性,设计了结合SDE[23]和欧式距离的适应度值计算方式用于环境选择算子,以平衡进化过程中的收敛性和多样性,并且环境选择还采用了循环淘汰的方式为下一代种群选择优秀的个体.
2.1 算法总体描述
为了同时优化本文所提出的3个目标函数,本文提出了MOEA-FMES.如前文所述X表示一个缓存方案矩阵,表示某个SBS是否缓存某个内容,因此本文的多目标进化算法采用二进制编码方式,种群数量记为L.
多目标进化算法总体流程如算法1中伪代码所示.首先进行初始化设置,包括初始化种群,产生L个个体;通过混合均匀设计方法在单位超平面上精确返回L个具有M个目标的均匀分布点;对目标值进行归一化处理,并将每个个体关联到余弦距离最近的参考向量上,从而完成初始种群划分.然后开始进化过程,直到达到最大迭代次数:计算参数θ;根据匹配选择算子选择父代种群;进行交叉变异操作产生子代种群;将父代与子代合并,并进行归一化处理;根据环境选择算子选择最优的前L个个体作为下一代种群.
算法1.多目标进化算法框架
输入:种群数量L
输出:最终解集
1.Create an initial parent populationP
2.Generate L reference vectors W according to the MUD method
3.W=MUD()
4.Normalize objectives of members inP
5.P′:= Objective_Normalization (P)
6.Associated reference vector:
7.E(i)=Associate(P′, W)
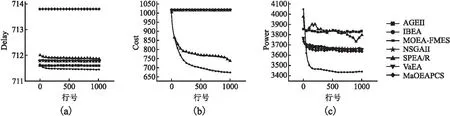
8.while t 9. θ is calculated by Eq.8 10.P=FarthestSelection (W,E(i)) //Select the P by Matching Selection Operator 11. O=GA(P)//The Offspring population O was generated by GA 12.G=P∪O 13.G′=Objective_Normalization(P) 14.P=Environment_Selection(G′,W,θ); 15.end while 匹配选择的目的是通过高质量的父代个体进行交叉、变异,从而产生优秀的子代,是进化算法的重要组成部分.本文的匹配选择通过选择两个最远子种群中的个体即余弦距离最远的参考向量所关联的个体来组成父代种群.伪代码如算法2所示.首先通过使用公式(11)计算所有参考向量之间的余弦距离: θ=(FE/maxFE)2 (11) 然后开始选择:从参考向量集中选择一个w,随机选择一个w关联的个体添加到Parent1中并从当前种群中删去该个体,选择w余弦距离最远的参考向量w′,之后随机选择一个w′关联的个体添加到Parent2中并从当前种群中删去该个体.循环结束后合并Parent1,Parent2. 算法2.匹配选择 输入:参考向量W,个体关联的参考向量集合E(i) 输出:用于交叉变异的父代种群P 1.Wdis=cosθ(W)//by Eq.(12) 2.while length/(Parent1) 3. for w=W 4. p1=random(E(i)==w) 5. Parent1=[Parent1,p1] 6.w′=max(Wdis(w)) 7. p2=random(E(i)==w) 8. Parent2=[Parent2,p2] 9. end for 10.P=[Parent1, Parent2] 11.end while σ=(FE/maxFE)2 (12) (13) 环境选择的目的是从合并后的种群中选择优秀的个体组成新的种群,新的种群应当确保个体之间保持收敛性和多样性的平衡,从而不断优化种群.在本文的设计中,环境选择参考了SPEA/R[27].与SPEA/R不同的是:本文替换了适应度的计算方式,且不同于SPEA/R的适应度以多样性优先、收敛性第二,本文根据迭代次数动态的调整多样性与收敛性的关系;SPEA/R在一个选择循环完成后进行下一轮循环,而本文在一个选择循环完成后会删去被选择的个体并重新评估剩余个体再开始下一轮循环. 环境选择循环的从各个参考向量的关联个体中进行选择.在每一轮开始时首先计算当前种群中个体的适应度值,然后从每个参考向量周围选择适应度值最小的个体(求解最小化问题时),选择完一轮之后将选择的个体添加到下一代种群中并从当前种群中删去,直到新种群的数量达到种群数量L.之所以每选择一轮就重新计算剩余个体的适应度值,这是因为循环选择的目的是均匀的选择参考向量所划分的子种群中的优秀个体,以选择高质量的解并提高解的均匀性,而本文在适应度的计算中考虑了个体之间的密度信息,一轮选择循环结束之后剩余个体之间的密度信息必然会发生变化,因此有必要对剩余个体进行重新评估.虽然重新计算适应度增加了计算量但能够更好的评估剩余个体的优劣.环境选择的伪代码如算法3所示. 算法3.环境选择 输入:归一化目标值P′,参考向量W,平衡参数 输出:NextP,E 1.E=Associate(P′,W)//Associate reference vector 2.while length(NextP) 3. Fit=(P′,E,σ) 4. for each reference directioni∈W 5. if E(i)≠Ø 6. q=argminp∈E(i)Fit(p) 7. Save q to H 8. end if 9. end for 10. remove H from P and E 11.end while 为了验证本文提出的MEC缓存方法的有效性,本文基于MATLAB 2022a软件使用PlatEMO v3.3平台进行仿真模拟实验,参数设置如表1所示,并与5种多目标优化算法进行对比:AGEII[28]、IBEA[29]、SPEA/R[30]、NSGAII[31]、VaEA[32]、MaOEAPCS[33].为了保证结果的可靠性,对比算法的参数设置保持默认设置. 表1 仿真参数表Table 1 Simulation parameter table 本文使用Spacing[34]、IGD[35]来进行性能评价,这两个指标被广泛使用的评估多目标优化算法,分别用于评价算法的解的多样性、综合性能. 1)Spacing metric (SP): (14) 2)Inverse generation distance (IGD): (15) P为解集,P′为从前沿面上采样的一组均匀分布的参考点,d(i,j)为参考集中的点i与解集中的点j之间的欧氏距离. 在多目标问题中,每个算法都会最终给出一组非支配解集,供决策者进行决策,解集中的每个解在不同目标上的各有优劣. 表2中给出了AGEII、IBEA、NSGAII、SPEAR、VaEA、MaOEAPCS和MOEA-FMES在本文提出的MEC缓存模型上计算得到的SP、IGD值.表中用黑体着重标出了最优值,并在每个数值的后面用‘+’、‘-’、‘=’标注了对比算法与MOEA-FMES的对比情况,分别表示优于MOEA-FMES、弱于MOEA-FMES和与MOEA-FMES持平.结果显示在IGD上MOEA-FMES表现最好,说明MOEA-FMES覆盖了真实的帕累托前沿面,能够给出一组高质量的非支配解集,SPEA/R和NSGAII在IGD上较为接近MOEA-FMES,而其他算法表现较差.在SP上,MOEA-FMES表现最好,说明所提出算法的解集最为均匀,种群的多样性最好,SPEA/R在SP上的表现较为接近MOEA-FMES,而AGEII性能最差,说明其给出的解集分布不均匀,多样性较差. 表2 评价指标对照表Table 2 Comparison table of evaluation indicators 表3中给出了AGEII、IBEA、NSGAII、SPEAR、VaEA、MaOEAPCS和MOEA-FMES对本文模型上的影响情况.通过对比不同算法给出的最终解集的不同目标值上的最优、最差、平均值来评估算法的优劣.可以看出MOEA-FMES在3个目标值上的平均、最优和最差表现均优于其他算法,表现出了良好的整体性能.具体来说在延迟方面6种算法的表现相似,无论是最优、最差还是平均值MOEA-FMES的领先幅度都很小;在缓存成本上MOEA-FMES和SPEA/R在平均、最优和最差上对于其他算法都有明显优势,且MOEA-FMES均能取得最优结果,说明MOEA-FMES能够有效的降低缓存成本;在传输功耗方面,虽然六种算法的最优值和平均值区别较小,但在最差值上VaEA与其他算法的差距很大,MOEA-FMES在最优、最差和平均值上都优于其他算法,说明MOEA-FMES能够有效降低传输功耗. 表3 6种算法在3个目标上的目标值Table 3 Target values of six algorithms on three targets 图3中的折线图显示了AGEII、IBEA、NSGAII、SPEAR、VaEA、MaOEAPCS和MOEA-FMES求解本文模型的3个目标的收敛情况.本文仿真实验最大迭代次数设为1000,可以看出在前300代收敛速度较快,之后收敛速度不断放缓,在约900代之后收敛程度基本没有变化.MOEA-FMES能够使得3个目标均有效收敛,且表现最好,SPEA/R虽然也能使3个目标共同收敛,但在传输功耗上的收敛程度较差,而其他算法则仅能使个别目标收敛,其余目标上几乎不收敛,导致曲线重叠,最终的收敛折线图直观上不易观察到每个图像的收敛程度,且收敛程度较低,陷入了局部最优. 图3 解集收敛图Fig.3 Convergence plot of the solution set 图4中的散点图显示了AGEII、IBEA、NSGAII、SPEAR、VaEA、MaOEAPCS和MOEA-FMES求解本文模型得到的解集分布情况,图中每一个小球代表一个解.可以看出SPEA/R的解在空间中的分布呈长条状,MaOEAPCS的解集虽然分散较为均匀但最终保留的解个数过少,AGEII的解主要分布在空间的上半部分,IBEA、NSGAII、和VaEA的分布范围较为均匀、接近,MOEA-FMES解在空间中的分布最为均匀,表明解的多样性较好,在3个目标上均进行了有效的探索. 图4 解集分布图(a~g分别为AGEII、IBEA、NSGAII、SPEAR、VaEA/MaOEAPCS和MOEA-FMES)Fig.4 Solution set distribution diagram (a~g is AGEII, IBEA, NSGAII, SPEAR, VaEA, MaOEAPCS and MOEA-FMES, respectively) 这是由于MOEA-FMES的环境选择在循环选择中不断地重新评估剩余个体,动态地调整收敛性和多样性的关系,从而使得选出的个体具有更好的代表性,在匹配选择时从两个最远子种群中随机选择个体来组成父代种群,因此MOEA-FMES不仅能够探索更多的解空间,解集的多样性更好,还能避免解集陷入局部最优,使算法更快地收敛且3个目标均能收敛到最优. 以上分析说明本文提出的MEC缓存模型是合理的,并且本文提出的优化算法在求解所提出的缓存模型时能够同时优化3个目标,最终给出一组收敛性好且分布均匀的非支配解集供决策者选择. 针对MEC缓存资源紧张的问题,为了提升系统整体性能,使得各个利益相关方均能从MEC中获益,本文提出了一种兼顾延迟、缓存成本、传输能耗的多目标缓存模型.为了更好的求解提出的模型,提出了一种基于最远交配和淘汰策略的多目标进化算法(MOEA-FMES),通过从具有最远余弦距离的参考向量周围选择个体的方式来选择父代个体,通过循环淘汰机制从各个参考向量的关联个体中进行环境选择,由于淘汰个体后会导致剩余个体的密度信息发生改变,所以每一轮选择开始前需要重新评估剩余个体.为了评估提出的MOEA-FMES,本文进行了模拟仿真实验,在IGD、Spacing上均表现优秀,并分析了算法的性能.在未来的工作中,将进一步完善缓存模型、改进算法来提高系统整体性能,如考虑用户偏好的动态变化;多个用户之间的优先性;考虑用户的移动对缓存性能的影响.2.2 匹配选择
2.3 适应度计算

2.4 环境选择
3 实验与总结
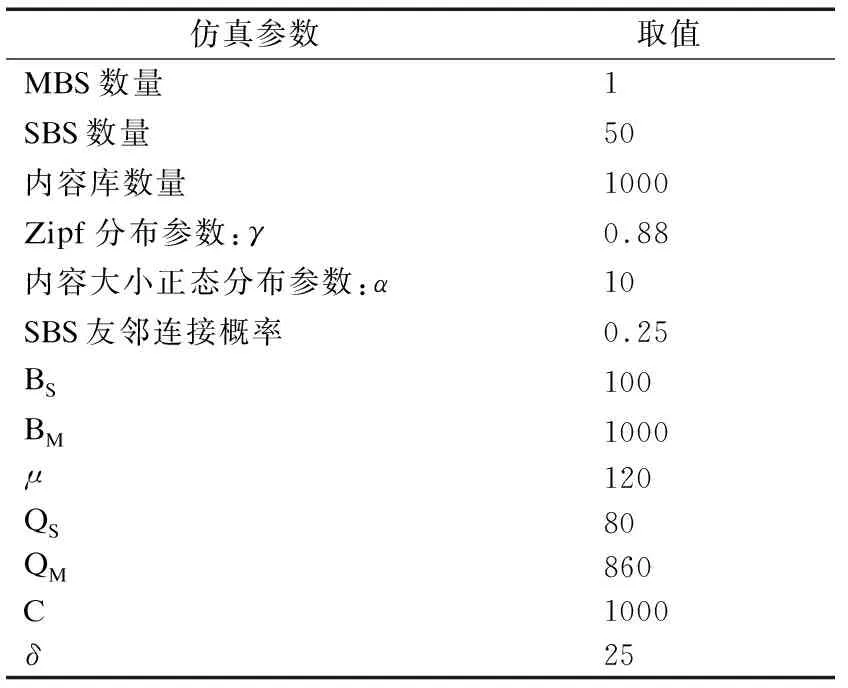
3.1 实验设计
3.2 评价指标
3.3 结果分析



4 总 结

