基于改进积分不等式的时变时滞系统稳定性分析

李紫薇,姜偕富,李敬莹,李佳峰,马雪乐

(杭州电子科技大学自动化学院,浙江 杭州 310018)

0 引 言

时滞在实际系统中十分常见,如数字控制系统、气动系统中的长传输线、制造过程和远程控制系统中都存在时滞,时滞已成为致使系统性能差甚至不稳定的主要原因之一。在过去的几十年里,由于时滞在许多实际系统中都会出现,导致一些不适当的性能、振荡甚至不稳定,人们对时滞系统的稳定性分析付出了大量的努力,主要集中在以下几个方向:一种方法是找到一个合适的L-K泛函;例如,LKF延迟分区方法[1],LKF增强项[2],LKF三重积分及四重积分项[3]等等。另一种方法是通过发展各种不等式技术,如Jensen不等式[4]、基于Wirtinger积分不等式[5]、Bessel-Legendre不等式[6]等。此外,为了进一步提高求解LMI的自由度,在LKF的导数中经常引入额外的自由加权矩阵技术,如零等式[7]、自由加权矩阵[8]等。其中,Bessel-Legendre积分不等式可以极大程度地减少所得到的结果的保守性。对于恒延迟系统,Bessel-Legendre积分不等式有得到解析解的潜力。然而,它在时滞系统中的应用中存在一个缺点,即它所得到的边界依赖于互凸组合。对于具有时变时滞的系统,通过引入松弛矩阵,Lee等人提出了一个affine Bessel-Legendre积分不等式(ABLI)[9]。然而其松弛项是与延迟无关的,其中的自由度还没有得到充分的反映,这导致了一定的保守性。受参考文献[10]的启发,本文通过插入一对凸参数,给出了一个基于松弛矩阵的复合积分不等式(CSMBII)。该不等式有以下两个优点。

(1)避免了Bessel-Legendre积分不等式中时滞变量h(t)出现在分母中这一情况,能更方便地处理时变时滞系统。

(2)解决了ABLI积分不等式中的松弛矩阵与时变时延无关的问题[11],使得CSMBII能进一步捕获时变时延和系统状态之间的耦合信息。在此基础上,针对时滞系统导出了一种新的稳定性判据。通过两个数值例子,验证了该准则的有效性。

1 问题描述

考虑以下线性时变时滞系统:

(1)

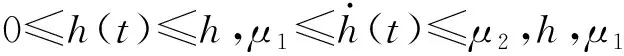
引理1(Bessel-Legendre积分不等式)[6]对于任意正定矩阵R和任意一个连续可微函数{x(s)|s∈[a,b]},对于所有整数N,以下积分不等式成立:

(2)

引理2(ABLI)[9]给定对称矩阵R>0,任意矩阵X和一个连续可微函数{x(s)|s∈[a,b]},对于所有整数N,以下积分不等式成立:

(3)

其中:

引理3[12]对于一个给定的二次函数f(y)=a2y2+a1y+a0,其中ai∈R,i=0,1,2,且0≤y=h(t)≤h,如果满足以下条件:

(1)f(0)<0;(2)f(h)<0;(3)-h2a2+f(0)<0;

则有:f(y)<0,其中y∈[0,h]。

引理4(CSMBII) 对于满足系统(1)的时滞变量h(t),任意正定矩阵Ri(i=1,2),任意连续可微函数{x(t)|t∈[-h,0]},及松弛矩阵Xi(i=1,2),存在参数α,β∈[0,1],且满足α+β=1,使得下面的不等式成立:

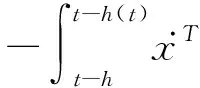
(4)

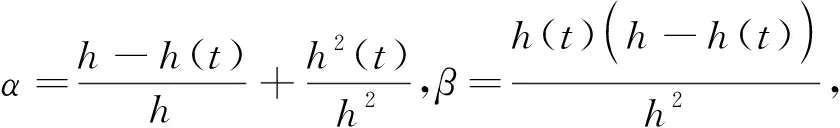
证明根据引理2和引理3可得:

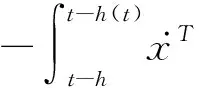
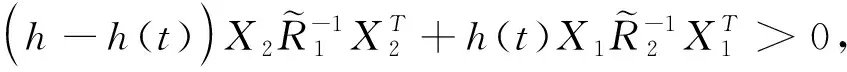
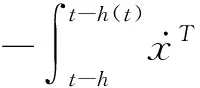
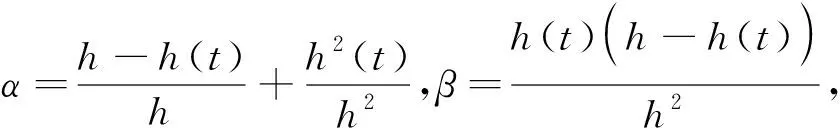
注2:从式(4)中可以看出,Bessel-Legendre不等式前的分数由于参数β的存在可以被消去,进而可以避免时滞变量h(t)出现在分母中的情况,使得该不等式能更方便地用来处理时滞系统;同时,可以看出(X1H+X2H)这一松弛量由于参数α的存在与时滞变量h(t)相关,使得其可以更多地捕获时滞变量与系统状态之间的耦合信息,故引理4综合了引理2与引理3的优点,预期可以得到一个保守性较小的稳定性准则。后续将围绕引理4给出一个系统(1)的稳定性判断准则并通过数值示例来说明运用该不等式的优势。

2 主要结果

(5)

(6)

(7)

则系统(1)渐近稳定。其中:

G2[h(t)]=[h(t)e7e1-e2h(t)(e1-e7)h(t)(e7-e2)],

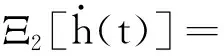
E1=[e1e2e7e9],E2=[e2e3e8e10],

ei=col{0(i-1)n×n,In,0(10-i)n×n},i=1,2,…,10.

证明首先,构造如下形式的L-K泛函,

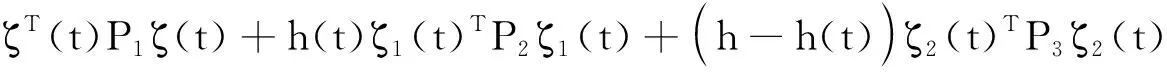
式中:

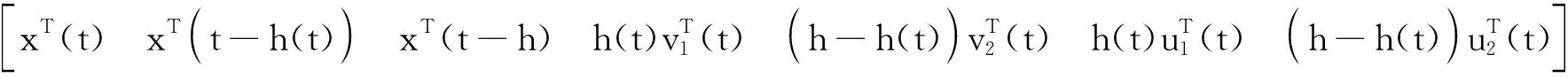
基于系统(1)的轨迹求取V(t)的时间导数:

其中:

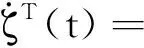
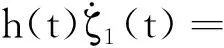
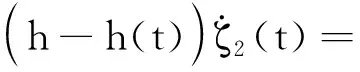
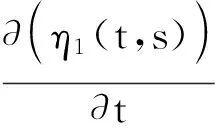
由引理4(N=2)易知:

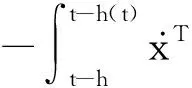
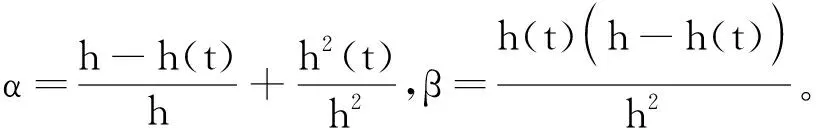
综上,对V(t)求导可得:

当

(8)

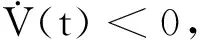
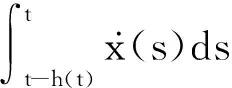
3 数值算例

本节通过两个例子验证了本文提出的稳定性准则的有效性。

首先,针对时滞系统(1)考虑了以下两个系统模型,这些系统模型在许多文献[9,11,13,14,15]中被广泛用于验证稳定性准则的有效性。

例1使用文献[13]中的系统模型:

(9)

令μ=-μ1=μ2,运用定理1计算了不同μ={0.1,0.2,0.5,0.8}的时滞系统(1)的最大时滞上界h,将本文所得最大时滞上界h与文献[9,13,14]对比,得到的结果如表1所示。

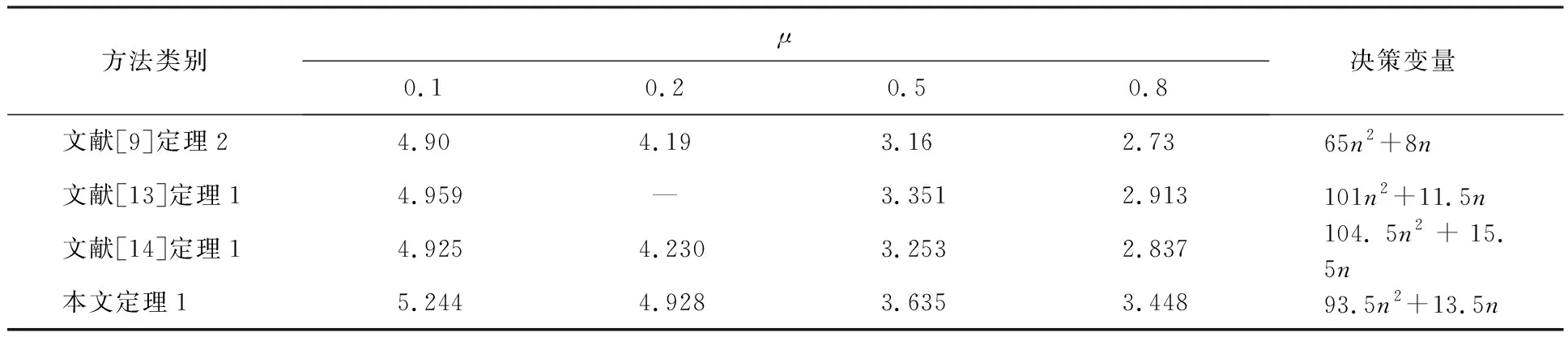
表1 例1中具有不同μ值的最大允许时滞上界h

对于给定的μ,时滞系统(1)的最大时滞上界h如表1所示,显然,本文定理1所得的结果要优于文献[3,5,12],且本文定理引入的决策变量相对文献[3]和文献[5]而言更少,在一定程度上降低了计算复杂度。

例2使用文献[5]中的系统模型:

(10)

令μ=-μ1=μ2,运用定理1计算了不同μ={0.1,0.2,0.5,0.8}的线性系统(1)的最大时滞上界h,将本文所得最大时滞上界h与文献[2,5,14]对比,得到的结果如表2所示。

表2 例2中具有不同μ值的最大允许时滞上界h

对于给定的μ,如表2所示,本文定理1得到的最大允许时滞上界h最大。因为本文运用了基于松弛矩阵的复合积分不等式(CSMBII),并在此基础上在积分泛函中补充了两对积分项的修正L-K泛函,考虑了更多的时滞相关信息,有效减小了结果的保守性。

通过上述2个数例的验证可知,使用CSMBII的定理1可以得到较小保守性的稳定性结果。

4 结束语

本文研究了时变时滞线性系统的相关稳定性问题。给出了一个基于松弛矩阵的复合积分不等式(CSMBII),基于该不等式,构造一个适当的L-K泛函,基于新的L-K泛函和引理4,导出了一个具有较小保守性的稳定性准则。最后,给出了两个数值例子,证明了该方法的有效性。但是,本文并未考虑非线性因素,下一步将本文方法应用于非线性时滞系统的相关研究中。