基于DE-SARSA(TS)的跳频系统智能抗干扰决策算法

袁 泽,赵知劲,2

(1.杭州电子科技大学通信工程学院,浙江 杭州 310018;2.中国电子科技集团第36研究所通信系统信息控制技术国家级重点实验室,浙江 嘉兴 314001)

0 引 言

随着信息化程度的提高,电磁干扰环境日益复杂,要保障信息的可靠传输,对通信系统的抗干扰能力提出了更高、更严的要求[1]。传统的跳频通信已经不能满足对抗干扰的需求,期望能够根据干扰环境自适应改变跳频通信系统的带宽、跳速、频率序列等参数,进行智能抗干扰。传统优化算法的抗干扰效果不佳,免模型的强化学习通过试错与动态环境交互具有更快的收敛速度[2]。文献[3]提出了一种改进Q学习算法HAQL-OSGM,并将其应用于跳频通信的跳频图案决策,提升了系统的收敛速度和抗干扰能力。对比于Q学习,SARSA学习是在线学习且注重学习期间所获奖励,具有更强的适应性[4],已在通信系统不同模块如EH-MQAM点对点无线通信系统的资源分配[5]、动态基站休眠[6]、认知无线网络抗恶意干扰[7]和水声通信自适应调制[8]等方面得到应用。近年来,在传统SARSA学习的基础上,有多种改进算法被提出。文献[9]将SARSA学习与卷积神经网络相结合;文献[10]将Q学习和SARSA学习相结合,得到反向Q学习;文献[11]采用自适应归一化径向基函数(ANRBF)网络对奖励进行整形,得到梯度下降(GD) Sarsa(lambda)算法;文献[12]应用期望SARSA(Expected Sarsa)算法,消除了SARSA选择动作而带来的误差;文献[13]在动作选择策略上使用模拟退火算法取代ε-greedy策略,加快了收敛速度;文献[14]引入线性近似方法得到一个近似的SARSA学习,平衡了算法的复杂度和性能之间的矛盾;文献[15]将SARSA学习引入到深度Q网络中,消除Q网络过高的估计;这些改进更好地平衡了智能体对状态空间的探索和利用,加快了收敛速度,提升了稳定性。但是由于采用的是无模型的SARSA学习,当状态动作空间比较大时,算法的收敛速度将变慢。文献[16]利用强化学习中的Dyna框架,提出了一种基于Sarsa-Dyna的自动驾驶路径规划算法,将无模型与有模型的优势互补,提高了算法收敛速度,有效地保证了路径规划的效率和安全性。上述算法都采用ε-greedy或Bolzmann这两种常用动作选择策略,ε-greedy策略存在盲目性导致收敛速度较慢;Bolzmann策略很少选择概率较小的动作,容易陷入局部最优。对此,本文采用汤普森采样(Thompson Sampling)算法作为动作选择策略,同时结合期望SARSA和Dyna框架的思想提出一种改进SARSA算法DE-SARSA(TS),平衡了探索与利用的矛盾,提升其收敛速度和稳定性,并将DE-SARSA(TS)算法应用于跳频系统智能抗干扰决策,得到了优于HAQL-OSGM[3]的结果。

1 问题建模

不同的干扰环境下,跳频通信系统通过改变其跳速、跳频序列和信道划分间隔等参数,从而大幅提高其抗干扰能力。首先通过频谱感知来估计未来N个时隙的信道干扰参数,之后设置跳频通信主要参数,其中信源速率c固定,信源功率p、跳频序列K、信道带宽B和跳频速率v则根据干扰情况自适应调整。

由香农公式可知,影响通信系统最大信息传输速率的参数主要为信道带宽B和信干噪比(Signal to Interference to Noise Ratio, SINR),如式(1)所示

c=Blog2(1+SINR)

(1)

其中,信道带宽B为决策参数,而式(2)所示的信干噪比SINR是度量通信系统通信质量可靠性的一个主要技术指标,信干噪比越大,系统的通信质量越好。

(2)

其中,hn为第n个时隙的信道增益,其服从瑞利分布;p为信源功率;Jn是第n个时隙的加性干扰功率;n0为噪声功率(默认为高斯白噪声)。

但在干扰和噪声功率一定的情况下,提高信干噪比需要更高的发射功率,增加了系统能耗。所以需要控制系统的能耗。在满足通信质量的情况下尽可能控制发射功率不会过高,因此本文将每个时隙的能量效率Φ作为决策目标,即:

(3)

2 算法设计

2.1 期望SARSA学习

SARSA是一种同轨策略下的时序差分学习,顾名思义,其更新公式中包含五个值:当前的状态值st,当前状态对应的动作at,即时奖励rt+1,下一个新的状态st+1以及所选择的新动作at+1。类似于蒙特卡洛方法,SARSA学习就是价值迭代,通过更新价值函数,进一步更新当前策略,再通过新的策略从而得到新的状态和即时奖励,一直迭代下去,最后使价值函数和策略都收敛。具体如图1所示

图1 SARSA流程图

图2 Dyna结构图

相比于传统SARSA,期望SARSA的形式与SARSA一样,都是根据状态s和动作a,计算出相应的动作价值函数,只是更新的目标变成了Q的期望值,更新公式如式(4)所示。虽然计算量增大,但可以消除SARSA中选择at+1时带来的误差,提升学习效果。

(4)

其中,Qt(st,at)是经过t次迭代后,状态st对应动作at的价值;π(a|st+1)是选择动作a的概率,则Qt(st+1,a)是该动作的价值;rt+1是执行第t次动作的即时奖励;参数μ∈(0,1)是学习率(learning rate),表明对此次误差的学习程度;参数γ∈(0,1)是衰减因子(attenuation factor),表示对未来收益的重视程度,γ值越大,算法就越会考虑后续收益的影响。

2.2 动作选择策略

传统算法大多采用ε-greedy或Bolzmann作为动作选择策略。ε-greedy算法虽然使每个动作都有被选择的概率,但由于这种选择太过随机,当状态动作空间比较大时,并不容易找到最优动作,最后导致收敛速度缓慢。Bolzmann算法使每个动作被选择的概率有所不同,但概率很小的动作很难被选中,选择的动作缺少多样性,探索度有所欠缺。对此,本文将基于汤普森采样算法的动作选择机制引入期望SARSA学习,汤普森采样是运用Beta分布求解最优解。Beta(α,β)表示连续概率分布函数族,且区间为[0,1],α和β为形状参数,Beta分布的概率密度函数形式如下

(5)

Beta分布的均值为α/(α+β),它的均值越大,概率密度分布的中心位置越接近1,因此其产生的随机数也都接近1,反之则都接近0。Beta分布的方差如式(6)所示,可以看出,如果(α+β)的值越大,则分布会越窄,产生的随机数分布更集中在中心位置。

(6)

本文将α设为Gt(st,a)+λ,β设为Bt(st,a)+λ,其中,Gt(st,a)是动作奖励值,Bt(st,a)是动作惩罚值,λ是初始参数,在某一状态下,选择一个动作后,如果其奖励比较大,则导致α增加,反之则β增加。在开始阶段,α和β都很小,分布较宽,有着很好的探索作用;随着选择次数的增加,(α+β)的值逐渐增大后,其分布变窄,产生随机数也在中心位置附近,进入利用阶段。如果一个动作的α值远大于β值,那么其分布很接近于1,即为好的动作,反之则为差的动作。Gt(st,a)和Bt(st,a)的更新公式为

Gt(st,at)=Gt(st,at)+Qt(st,at)*Qt(st,at)

(7)

Bt(st,at)=Bt(st,at)+1/Qt(st,at)

(8)

在t状态下,动作的奖励收益越大,其Gt(st,at)越大,Bt(st,at)越小,动作的奖励收益越小,则Gt(st,at)越小,Bt(st,at)越大。汤普森采样算法在前期增大了选择的随机性,更好地对状态动作空间进行探索,随着选择次数的增加,分布变窄减小随机性,使最佳动作被充分的利用,提升了系统的收敛速度和稳定性。

为进一步提升学习效率,本文在初期更多地对未选择过的动作进行遍历探索,避免算法陷入局部最优,利用tanh函数的特性,定义收敛函数如式(9)所示,设计的动作选择策略如式(10)所示

S(t)=(tanh((t/ε)-η)+1)/2

(9)

(10)

其中,t为迭代次数;ε和η为特定参数,其中ε决定了探索度的大小;ax是P表中值为0的动作,即未被选择过的动作,表P(st,at)记录动作被访问的次数,每次选择动作后,P表中对应值加1;rand为分布在0～1之间的随机数。随着迭代次数t的增多,函数值S(t)逐渐由0平稳上升为1,因此可以在前期进行更加充分探索,使系统有更快的收敛速度。

2.3 状态动作空间和奖励函数设计

本文定义系统状态st是当前跳频信号对应的时隙,定义可选动作at是信源功率p、跳频序列K、信道带宽B和跳频速率v的离散组合。对应不同的时隙,智能体通过与环境交互进行自适应学习找到最佳动作,即信源功率p、跳频序列K、信道带宽B和跳频速率v的最优分配方案,最大程度地规避各种干扰,得到最适合当前环境的跳频图案。

本文的决策目标是每个时隙的能量效率Φ最大化,因此设计奖励函数如下:

(11)

(12)

其中,Rt+1是第t次迭代中得到的平均奖励值;rn是第n个时隙的瞬时奖励,其满足正态分布,均值为Φ,方差为σ2;Cn为信道容量,可由式(1)得到,Φ为每个时隙的能量效率,可由式(3)得到;θ为参数,用于调整Q值与Rt+1之间的平衡,当奖励过大时,会导致Q值过大,超出计算机的储存上限,奖励过小时,则会导致Q值更新缓慢,从而影响系统的收敛速度。

2.4 Dyna算法框架

在面对复杂多变的电磁环境时,不基于模型的强化学习性能提升有限,学习模型可能会有更好的效果,但单纯基于模型不可能精确和完美地拟合环境,会导致模拟的结果与实际存在误差。为了避免上述弊端,本文引入Dyna算法框架,将模型学习和强化学习结合起来。下图为Dyna结构。

从上图中可以发现,首先通过与环境交互得到实际经验,然后从两个方向对决策进行更新,右边是通过无模型的强化学习直接进行更新,左边则是先通过实际经验建立一个模型,之后从模型中选择批量的模拟经验对决策进行规划更新。在本算法中,一定的干扰环境下,通过期望SARSA学习对Q表进行更新;用M表和E表存放模型信息,M表储存每个状态下不同动作的奖励,E表储存每个状态下不同动作对应的下一个状态,每次Q值更新时同步更新M值和E值;再随机选择多个已选择过的状态和动作,通过M表和E表对Q值进行规划更新。所以当智能体选择了一个动作后,同时通过实际的动作选择和环境模型的模拟对Q值进行更新,从而提升了系统的收敛速度和稳态性能。

2.5 算法步骤

由上得到结合汤普森采样动作选择机制和Dyna模型思想的期望SARSA学习算法(本文简记为DE-SARSA)步骤如下:

(a)估计未来N个时隙信道的干扰频谱瀑布图。

(b)设定参数μ,γ,λ,ε,η,θ,σ;设定学习迭代次数I,将各状态动作的Q值初始化为1,随机初始化状态s0和动作a0;对于Dyna模型,将M表和E表初始化为0,设定迭代次数J,随机选取遇到过的状态ns,随机选取执行过的动作na。

(c)i=0,重复I次循环:

(1)选择状态si和动作ai,由式(9)计算S(i),产生一个0～1的随机数,根据式(10)选择动作ai,根据式(3)、式(11)和式(12)计算奖励Ri+1并得到下一状态si+1;

(2)根据式(4)更新Q表,将每个状态下不同动作的奖励Ri+1储存在M表,将每个状态下不同动作对应的下一状态si+1储存在E表,根据式(7)更新G表,根据式(8)更新B表。

(3)j=0,重复J次循环:

①随机选择遇到过的状态ns,随机选择执行过的动作na,读取M表的奖励值Ri+1,读取E表的下一状态si+1,根据式(4)更新Q表。

②j←j+1。

(4)i←i+1。

3 算法仿真及性能分析

实验参数设置如下:时隙数N取100,取0-160 MHz作为总带宽,信源速率为5 Mbps,信源可选功率为{150,200,250,300} mW,可选信道带宽集合为{1,2,4,8} MHz,跳频速率为{500,1000,2000,4000}次/秒,可选频率序列满足在跳频频段内随机跳变的条件,共有8种,信道增益h服从瑞利分布,高斯白噪声功率n0取10-7mW,在仿真期间h和n0取值保持不变,μ=0.7,γ=0.3,λ=1,η=8,σ=0.2。单次实验迭代次数取20 000次,并分为20个学习阶段进行统计。10次独立实验结果的平均值作为仿真结果,将高斯白噪声、扫频干扰、窄带干扰和宽带干扰的组合作为干扰环境,其频谱瀑布图如图3所示。

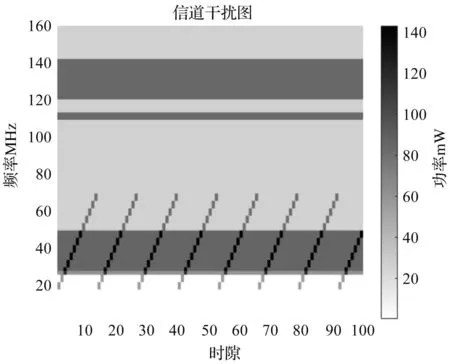
图3 干扰环境频谱瀑布图

3.1 参数θ和ε对算法性能的影响

当参数θ取5,15,25,35,45时,使用本文算法后得到的系统能量效率曲线(a)如图4所示。当θ为25,参数ε取200,300,400,500,600,700时,使用本文算法得到的能量效率曲线(b)如图5所示。

图4 系统能量效率曲线(a)

图5 系统能量效率曲线(b)

由图4可见,增大θ值,可以提升算法的收敛速度和稳态性能;当θ大于15时,算法的收敛速度没有显著提升,但稳态性能开始下降。根据上述结论,为了平衡奖励值和Q值,下文取θ为25。由图5可见,随着ε取值的增大,系统最终的能量效率逐渐升高,但收敛速度会下降,当ε取值大于400后收敛速度显著下降,但系统能量效率提升较少,为了平衡收敛速度和能量效率,下文取ε为400。

3.2 不同环境下算法性能对比分析

将基于ε-greed机制的经典SARSA学习、基于Boltzmann机制的经典SARSA学习、引入Dyna模型的SARSA学习依次简写为SARSA(ε)、SARSA(B)、SARSA-D。将本文算法DE-SARSA和SARSA(ε)、SARSA(B)、SARSA-D、期望SARSA学习(EX-SARSA)、文献[3]的改进Q学习算法HAQL-OSGM做性能对比,其中SARSA(B)、SARSA-D、EX-SARSA和改进Q学习算法HAQL-OSGM的初始温度参数T0都设为1,在如图6(a)-(c)所示的三种不同干扰环境中进行跳频通信系统智能抗干扰决策,对应得到六种算法的能量效率曲线如图6(d)-(f)所示,六种算法所需的平均运行时间和占用内存结果如图7和图8所示。

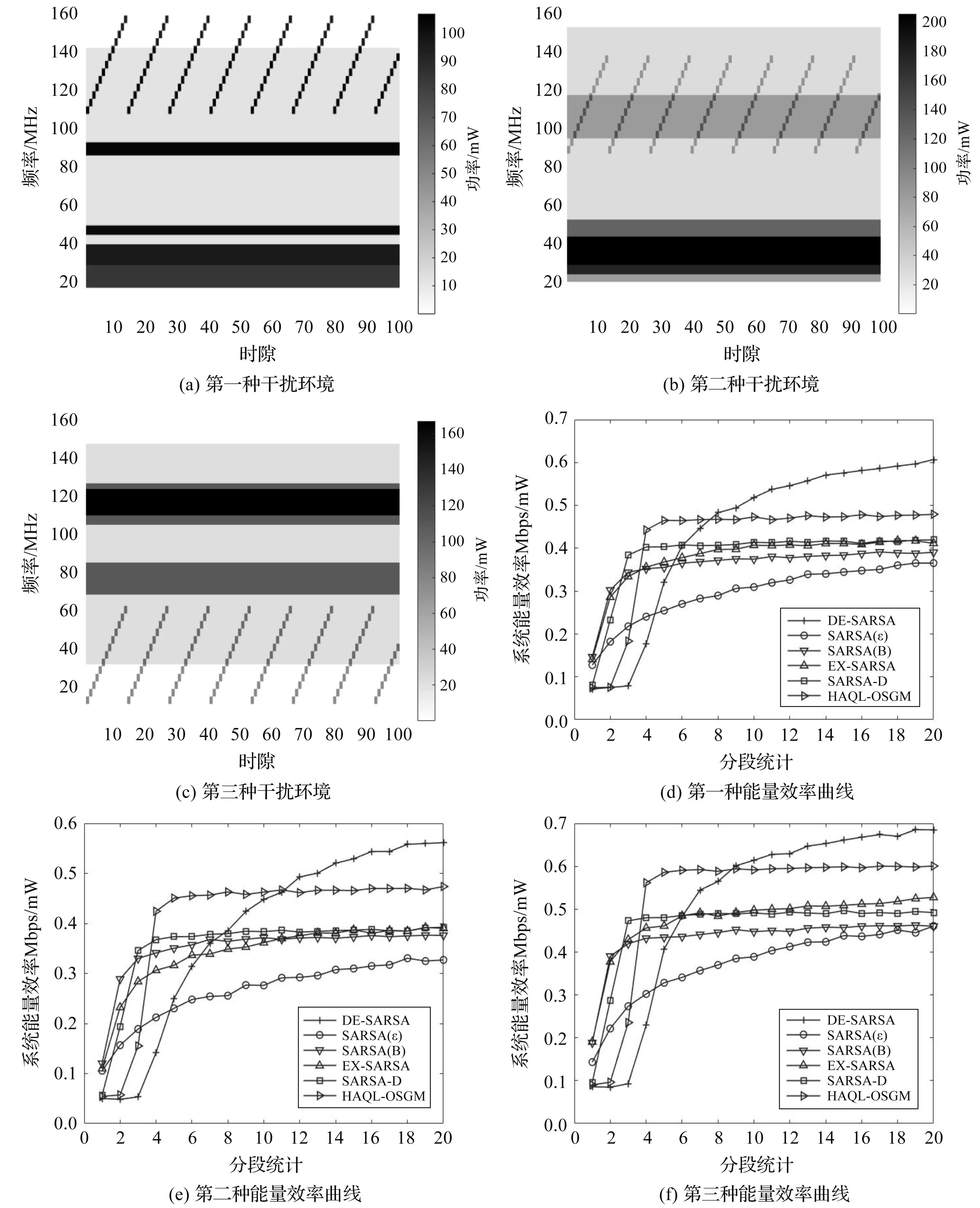
图6 三种干扰环境及相应的系统能量效率曲线

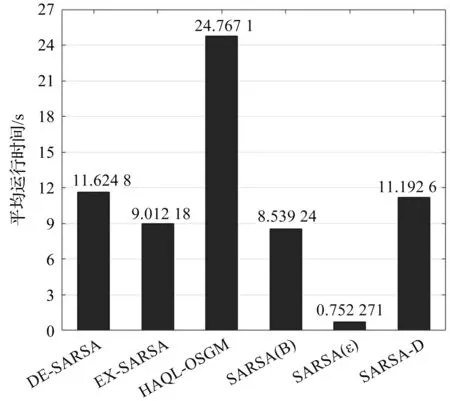
图7 平均运行时间条形图

图8 占用内存条形图

由图6可见:(1)与经典SARSA学习的SARSA(ε)和SARSA(B)相比,在不同干扰环境下,本文算法具有更快的收敛速度、更好的稳态性能以及更高的能量效率。说明了基于汤普森采样的动作选择机制优于ε-greedy机制和Boltzmann机制,对比其余算法虽然收敛速度略慢但稳态性能最高。(2)与SARSA-D和EX-SARSA相比,本文算法具有更多的能量效率。这是由于本文算法引入了期望SARSA消除了选择at+1时带来的误差,并且结合Dyna模型,使系统在强化学习更新的同时,利用之前学习的经验进行模拟更新,提升了系统能量效率。(3)与改进Q学习算法HAQL-OSGM相比,本文算法能够获得更高的能量效率,而且面对不同的干扰环境HAQL-OSGM算法需要调整其温度参数。总体来说,在不同的干扰环境下,本文算法都具有较快的收敛速度,可以处理复杂电磁环境中的决策问题,提升跳频系统的抗干扰性能。

由图7可见,本文DE-SARSA算法运行时间比HAQL-OSGM快一倍以上,与SARSA-D相近,略比EX-SARSA和SARSA(B)慢些,SARSA(ε)结构简单,运行时间最短。由图8可见,SARSA(ε)、EX-SARSA和SARSA(B)占用内存占用量相当且较低;本文DE-SARSA算法和SARSA-D算法内存占用量相当,略比前三者多,这是由于引入Dyna模型增加了更新次数所致;HAQL-OSGM内存占用最高。

综上可得,较其他对比算法,本文算法DE-SARSA在达到最大系统能量效率和较优收敛速度的同时,保持了较短的运行时间,占用内存比HAQL-OSGM少,因此综合性能最优。

4 结束语

为了进一步提高跳频通信系统的抗干扰能力,DE-SARSA算法引入基于汤普森采样算法的动作选择机制和Dyna模型思想到期望SARSA学习,并将DE-SARSA算法应用于跳频通信的智能抗干扰决策。仿真结果表明,DE-SARSA算法的综合性能优于五种对比算法,对干扰环境有更强的适应性。本文是将强化学习应用于小规模离散问题,未来将研究其在更大规模实际问题中的应用。