四相交错Boost变换器的解耦均流控制方法
马瑞雪, 马帅旗, 刘子菡, 邰 亮
陕西理工大学 电气工程学院, 陕西 汉中 723000
目前,交错并联技术广泛应用于电动汽车、光伏发电、储能系统等领域[1-3]。由于变换器中器件的差异性,导致变换器各相间电流不均衡,影响系统的可靠性[4-6]。目前,许多学者对交错并联技术的均流控制策略进行了研究,常用的均流方法主要有下垂法(Droop method)和有源法(Active current sharing method)[7-11]。有源法通过改变输出电压幅值来实现均流,又可分为平均均流法、最大电流法和主从均流法。下垂法是通过调节模块的输出阻抗,达到均流的目的。
文献[12]给出了一种电压环与均流环并联的控制方法,其输出占空比由电压环与均流环共同决定,输出结果稳定,但均流环调节时会导致输出电压的波动,控制环路之间存在耦合关系。文献[13]中给出了一种电压环与均流环解耦的主从均流法,通过选择不同的控制变量分析解耦条件,并给出新的占空比表达式,从而实现均流。文献[14]给出了一种单电流环与均流环解耦的主从均流方法,通过选择总输出电流和其中两相电感电流为控制量构建电流关系和占空比关系,对占空比进行控制实现均流。文献[12-14]本质上属于单环控制,当外部施加扰动时,系统的响应时间较长,难以满足现在大功率场合的需求。文献[15]在文献[13]的基础上将双闭环与均流环结合起来,在对单闭环快速进行补偿的同时,实现电流均流控制,取得了较好的均流性能。
本文以四相交错Boost变换器为研究对象,提出一种电压电流双闭环与主从均流环相解耦的控制方法,简化控制器设计,解决控制回路中双闭环与均流环之间的耦合问题。
1 交错并联Boost变换器工作原理及小信号模型
1.1 拓扑结构分析
四相交错Boost变换器的拓扑结构如图1所示,该变换器由4个Boost电路并联而成,且各相功率开关管的脉宽调制驱动信号相位依次相差90°。其中,Li和rLi分别为第i相Boost电路中的滤波电感和电感电阻,C为变换器的总输出滤波电容,R为输出负载。

图1 四相交错并联Boost变换器拓扑
1.2 工作模态结构分析
假设变换器工作在电流连续模式,根据4个开关管的状态,变换器可分为13种工作模式,其开关时序图如图2所示。

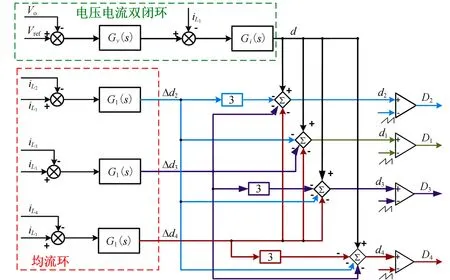
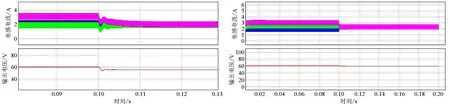
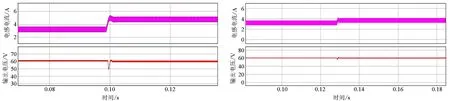
(a) D≤0.25 (b) 0.25 ① 占空比D≤0.25时,分为两个模式:单开通模式和全关断模式,两个模式依次交替变换。当处于单开通模式时,只有一个开关管导通,其他处于关断状态。若某相开关管导通时,该相电感电流处于充电模式;某相开关关断时,该相电感电流向负载R、电容C充电,处于放电模式。全关断模式时,4个开关管全部关断,电感电流iL1、iL2、iL3、iL4分别经二极管D1、D2、D3、D4向负载R和电容C充电,电感L1、L2、L3、L4处于放电模式。 ② 占空比0.25 ③ 占空比0.50 ④ 占空比0.75 采用开关网络平均模型法建立小信号数学模型,选择占空比D∈(0.75,1.00)的工作模态下的变换器模型进行分析,此时仅有全开通模式和三开通模式。 当处于全开通模式时,电感电压表示为 VLk(t)=Vin(t)-iLk(t)rLk, (1) 式中,VLk(t)为需要求解的电感电压,Vin(t)为输入电压,iLk(t)为电感电流,rLk为电感内阻。 当处于三开通模式时,断开相电感电压方程为 VLk(t)=Vin(t)-iLk(t)rLk-Vo(t), (2) 式中,Vo(t)为输出电压。 据伏秒平衡得到 (3) 式中,〈vLk(t)〉TS、〈vin(t)〉TS、〈iLk(t)〉TS、〈vo(t)〉TS分别为电感电压、输入电压、电感电流、输出电压在开关周期TS内的平均值,dk(t)为占空比交流分量。 对式(3)平均化,得到 (4) (5) 又因为平均变量可以分解为直流量与交流量,即 (6) 将式(6)代入式(4)、(5)中,忽略二阶交流小信号量,则小信号交流模型可表示为[16-18] (7) (8) 将小信号模型进行等效,其开关平均网络等效模型如图3所示。 图3 四相交错并联Boost变换器等效电路图 在同一个工作区间内,第k相开关导通,电感电流随之上升,此时电流纹波可表示为 (9) 同时,其余j相开关处于关断状态,电感电流下降,电感电流纹波和输出电压可表示为 (10) 其中ΔiLk为开关导通相电感电流纹波,ΔiLj为开关关断相电感电流纹波,k+j=4,且k≠j,TS为开关周期。 则总的输入电流纹波可表示为 Δiin=ΔiLk+ΔiLj。 (11) 用K(D)表示输入电流纹波与单相电感电流纹波的比值,可表示为 (12) 由式(12)可推导出四相电流纹波比值为 (13) 由图1可知,负载两端电压等于电容两端电压,则电容充电波形如图4所示。图中,IL为输出电感电流之和,Io为输出电流。在[t1,TS/4]时间内,电容电流为总电感电流与输出电流之差。根据电荷安秒平衡,输出电压纹波表达式为[19-20] (14) 图4 电容充电波形图 由式(14)得输出电压纹波为 (15) 传统的主从均流控制方法如图5所示,图中电感电流iL1所在相为主相,其占空比与负载电压和主相电感电流相关,其余相为从相,从相占空比由负载电压、主相及本相电感电流共同决定。均流环调节时会影响输出电压的波动,双闭环与均流环之间存在耦合关系。 图5 传统的主从均流控制方法 为了对电压电流双闭环和均流环之间实现解耦控制,在四相交错并联Boost变换器中,采用主从均流的控制策略。选择输出电压vo、主相电感电流iL1及主相电感电流与从相电感电流之差iL1-iLk作为控制量。 假设除了交流小信号占空比外,各项参数均相等,即Lk=L,rLk=rL,ILk=IL,Dk=D。由式(7)、(8)可得被控对象的传递函数表达式 (16) (17) (18) 综上所述,在设计双闭环时,使其输出信号不对dL1-dLk的值产生影响;而在设计均流环时,使其输出信号不对dL1的值产生影响,即可实现均流环与双闭环之间的解耦。若上述条件均满足时,即可使得各个控制环之间相互解耦。 基于上述解耦控制机理的分析,提出一种解耦的主从均流控制策略如图6所示。为了简化控制器设计,选取参数相等的均流控制器。Gv(s)、Gi(s)和G1(s)分别为输出电压环、电流环和均流环的PI控制器。其中双闭环控制器输出占空比基准值为d,均流控制器输出各相占空比补偿值为Δdk,两项叠加得到补偿后的占空比dk,实现电流均衡。 图6 解耦的主从电流控制方法 考虑到小的信号扰动,补偿后的占空比表示为 (19) (20) (21) (22) (23) 故可知,在双闭环控制器调节主从电感电流和输出电压的过程中,不会对均流环的控制效果产生影响;且在均流控制器调节不平衡电流的过程中,不会对主相电感电流、输出电压及其他的均流环产生影响,即可实现各个控制环之间相互解耦。最终达到均流环与双闭环解耦的目的。解耦后的控制结构图如图7所示。 (a) 电压电流双闭环 (b) 均流环 由第二节对电感电流纹波和电压纹波的分析可知,电感参数与电流纹波直接相关,电容参数与电压纹波直接相关。为了保证变换器每相都能安全可靠运行,所选电感、电容根据单相变换器参数进行设计,并根据工程经验取了一定的裕量。根据国家标准,电感电流纹波不应超过电流电流直流分量的20%,电感计算公式为 (24) 因为交错并联变换器能减小电流纹波的特性,因此在保证变换器能工作在CCM模式下的电感量,可根据实际需求适当减小电感设计需求,最终实际电感取值为L1=L2=L3=L4=600 μH。 同样,根据国家规定直流变换器电压纹波的要求,在不同工作模式下输出电压纹波幅值应不大于稳态输出电压的5%。根据前文理论,滤波电容应为 (25) 考虑一定的裕量,最终,电容实际取值为C=20 μF。 为验证上述理论方法的正确性,本文利用PSIM软件搭建了仿真平台。选择的电路参数见表1。将所提的控制方法与不解耦的均流控制方法和单电压环输出的控制方法进行了对比。仿真验证包括两部分内容,分别为均流环使能实验和负载跳变实验。 表1 变换器主电路设计参数 通过引入4个不同的电感内阻值进行解耦控制与不解耦控制的对比情况仿真,具体仿真结果如图8所示。令均流环在0.1 s开始动作,两种控制方法都能使电感电流快速实现均等并稳定。 (a) 不解耦均流控制 (b) 解耦均流控制 由图8(a)可知,当均流环使能之后,不解耦的控制方法使本不平衡的四路电感电流L1、L2、L3、L4虽能较快均流,但稳定时间较长,为Δt≈11 ms。同时,输出电压存在较为明显的波动,幅值ΔU≈5 V。说明均流控制器在平衡电感电流的同时影响了输出电压,即均流环和输出电压环是耦合的。 图8(b)为采用解耦控制方法时,均流环使能前后的仿真波形。相比于图8(a),当均流环使能之后,四路电感电流L1、L2、L3、L4均流速度相较于不解耦控制方法的11 ms,此方法仅用1.2 ms完成均流,性能明显优于不解耦控制。而且在此过程中,输出电压ΔU几乎保持恒定,幅值ΔU≈1 V。说明均流控制器对输出电压几乎无影响。通过对比输出电压波动幅值,证明了此方法的可行性。 图8(c)、(d)为两种方法的各相电感电流对比图,从对比发现不解耦控制方法中,在均流环动作后各相电感电流出现小超调,超调量约为15.5%,解耦控制方法中超调十分微小,可忽略不计,且不解耦均流控制电压电流稳定速度慢于解耦控制方法,也反映了方法优良的动态性能。 为了进一步验证本文研究方法的优越性,将本文方法与单闭环控制方法在负载跳变方面进行对比,图9给出了当负载跳变时两个方法的电感电流和输出电压对比波形。 (a) 单闭环控制 (b) 双闭环控制 图9(a)为单闭环控制方法下负载跳变仿真波形。当负载从15 Ω降低到10 Ω时,输出电压出现11 V左右的脉冲,经过3 ms的调整后稳定下来,在此过程中,电感电流均流并未出现影响,四相电感电流仍保持动态均流,但有较小的超调量波动,故采用单闭环控制器时,变换器的调节性能较差。 图9(b)为采用解耦的双闭环控制方法时,输出负载跳变前后的波形。相比于图9(a),当输出负载跳变时,输出电压波动较小,ΔU≈3 V,并且在3 ms内稳定下来。在此动态过程中,电感电流均流也无影响,保持较好的平衡性能。说明当负载跳变时双闭环对输出电压的调节并不影响均流环对电感电流的平衡。 本文就四相交错并联Boost变换器控制中存在的双闭环与均流环的耦合问题,提出了一个解耦的主从均流控制方法,通过对变换器原理分析与建模,通过选取不同的参考量,从传递函数上将双闭环与均流环分解,实现了双闭环与均流环之间的解耦控制。在此基础上搭建仿真平台,验证了此方法的可行性。仿真结果表明,当模拟实际中各相电路参数存在差异的情况下,在本文所提方法下,双闭环与均流环耦合程度较小。在负载跳变时,电压波动和调节时间都较小,具有良好的动态响应性能。在均流环设计时采用相同的调节系数,简化了控制器设计的复杂性,使变换器保持优异的动态性能,并实现双闭环与均流环的独立控制。1.3 小信号建模


2 纹波分析
2.1 电感电流纹波
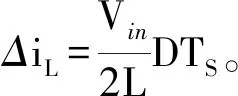
2.2 电压纹波

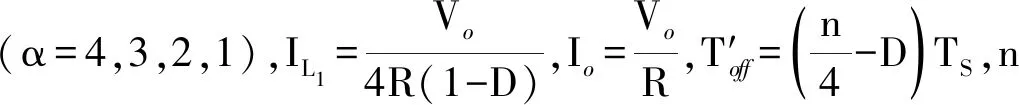
3 解耦的主从电流控制策略
3.1 解耦策略机理分析
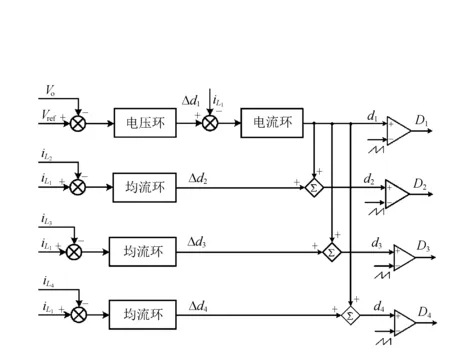
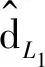

3.2 解耦均流控制策略

4 参数设计
4.1 滤波电感参数设计
4.2 输出电容参数设计
5 仿真与结果分析

5.1 解耦控制性能对比
5.2 负载跳变仿真对比
6 结论

