改进NSGA-Ⅱ算法的新能源储能系统协调优化模型

向 辉，史柯夫，陶 俊，乔 雄

（安徽继远软件有限公司，安徽合肥 230088）

当前，能源与环保问题日趋突出，新能源转型已是全球经济发展的一个重要方向。新能源储能系统中的供需不平衡和缺乏系统性，使得互联网技术逐渐成为推进新一代能源转型的重要技术。新能源储能是目前新一代网络技术发展的一个主要形式，也是当前技术发展主流趋势。然而，储能系统受多样化和运行方式复杂性的影响，在实际协调过程中面临储能难的问题。

文献[1]提出了考虑新能源消纳的协调方法，构建了区域新能源储能系统的数学模型，在此基础上，将其应用于多个新能源体系的求解，并对其进行动态调整，以达到网格化存储的目的。文献[2]提出了基于曲线波动度约束的协调方法，利用指标构建了含有相似性和波动性指数的两级协调优化模型，结合变分模态分解方法，分解差值序列，实现储能系统协调优化。以上所使用的方法简单直接，易于计算，但未考虑供求关系，需要进一步深入研究。为此，构建了改进NSGA-Ⅱ算法的新能源储能系统协调优化模型。

1 动态调节储能参数

为了解决新能源储能系统的最佳协同问题，采用NSGA-Ⅱ算法动态调节储能参数。新能源储能系统包括风电子系统、光伏子系统、储热子系统，这些子系统是以新能源耦合为基础进行能源交互的[3-4]。基于此，构建的新能源储能系统拓扑结构如图1 所示。

图1 新能源储能系统拓扑结构

在多个新能源系统中，不同的能源供应网络相互结合，且多个新能源网中的分布式存储单元具有多时间尺度的风电、光伏、储热的传输特性，使得多个子系统的建模必须同时考虑动态调节特征参数[5]。如果存在m个协调目标，那么使用NSGA-II算法定义协调目标i的拥挤度为：

式中，fj(i+1)、fj(i-1)分别表示协调目标i个体在第j次协调的优化值。由于每个新能源都具有可控制的负荷资源，所以在充分利用其降低费用和满足客户需求的前提下，采用适当的削减合约，实现其在满足各个目标前提下得到最大收益的新能源分配效果[6-7]。

2 改进NSGA-Ⅱ算法的协调优化模型构建

在每个协调周期内，新能源储能系统会展示所有的负载和减少的补偿量，而在新的能量存储层中，通过两阶段优化方式，分析用户趋势，调用合理负荷削减合同，调整新能源储能系统协调计划[8-9]。

2.1 协调指标确定

设置以新能源储能系统削减计划中最小偏差协调结果为目标函数，确定粒子初始位置，在c维空间内生成m个粒子，将该粒子位置描述为：

式中，i表示目标数量。对于不同粒子间的适应度，计算公式为：

式中，fmax(i)、fmin(i)分别表示协调过程中适应最大度和适应最小度；α表示适应因子[10]。选择协调目标中最大、最小的粒子作为最优适应协调依据，基于此，更新粒子最优位置，可表示为：

新能源储能系统的协调最优指标负荷可以分为三种：固定负荷、随机负荷和可迁移负荷[12]。相对于固定负荷的不可调节性和随机负荷的不确定性，可迁移负荷是指在一定时期内由使用者向其它时段进行负荷的转换，且是具有调节性的。

1）转移容量指标

在转出周期内的转出和转入期的输入电量均不能超过其最大值，即：

式中，tout、tin分别表示电量转出时段、电量转入时段；ΔQ表示电量转移差值；ΔQˉ表示转移电量最大值[13]。

2）负荷平衡指标

在全协调调度期间，各个时间段的转出负荷和转入负荷总数是相同的，因此，按照下列公式来表示传输之后的负荷：

式中，Q′(tin)、Q′(tout)分别表示转入时间段和转出时间段的迁移前负荷；Q0(tin)、Q0(tout)分别表示转入时间段和转出时间段的迁移后负荷[14]。利用高密度信息量对可转移负荷进行合理地规划是实现储能系统协同和优化的有效方法。

2.2 新能源储能系统协调优化模型构建

NSGA-II 算法在协调调度过程中，易出现局部最优化问题，但其对个体的协调调度效率较低，因此在NSGA-II 算法中引入量子搜索算法。该方法的主要特点是其控制参数大小，对NSGA-II 的改进，只对它自身特性的收缩扩张系数进行了计算[15]。为了提高粒子寻优定位精度，提出了一种可调整的收缩扩张系数，以确保粒子在初始阶段的多样性和准确性。其表达式为：

式中，βmin、βmax分别表示收缩扩张系数最小和最大值；Fit(f′)、Fit(fmin)分别表示所有粒子的平均适应度值和最小适应度值。将改进NSGA-II 算法应用到粒子寻优过程中，同时引入量子搜索算法能够有效改善系统寻优性能，并在改进NSGA-II 算法加入了新能源储存系统的网格化储能协调步骤，以提高系统整体协调效率。

网格化储能协调既要考虑单元间的协同合作特征，又要兼顾单元间的能量协同效应，还应考虑多能源单元间的传输容量。网格化储能协调是以消纳新能源的特点为依据，以存储单元的调整能力和传送能力为基础进行储能系统分区处理，达到网格化均衡消纳目的[16]。在整个划分区域内，定量分析新能源消纳调控程度，如图2 所示。

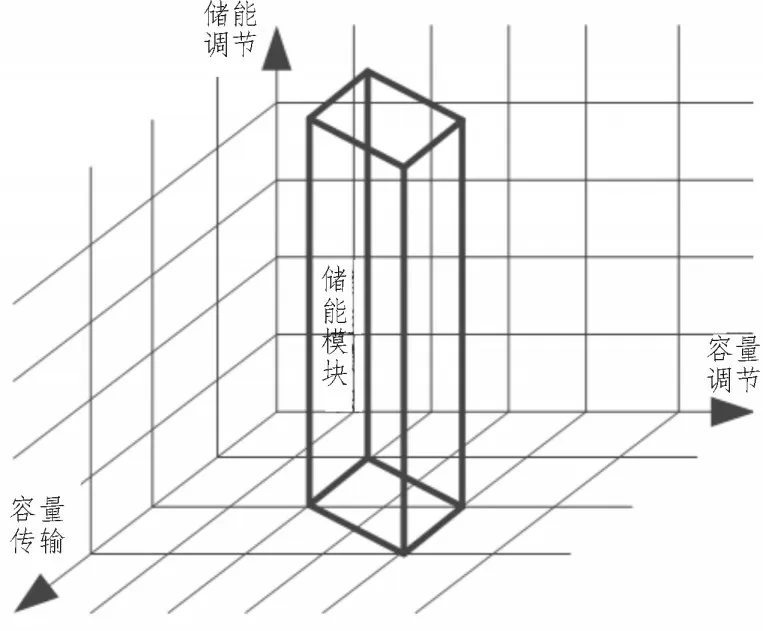
图2 网格化储能协调过程

基于此，构建的协调优化模型为：

式中，Pt、Pˉt分别表示t时刻能源被调度的负荷削减率和削减率上限；T表示协调周期，由此完成新能源储能系统协调优化模型构建。

3 实验分析

3.1 实验环境模拟

为验证构建的改进NSGA-Ⅱ算法的新能源储能系统协调优化模型的有效性，根据某区域新能源储能系统储能的实际情况，利用MATLAB 软件构建了包括能量管理、中央控制的储能方式，通过耦合系统模拟光伏逆变器、电力系统和锅炉，并采用CPLEX进行了实验[17]。新能源储能系统协调周期为24 h，单位协调间隔为10 s。基于此设计实验模拟环境，如图3 所示。

图3 实验环境模拟

由图3 可知，“光伏+风电+储热”将形成一种多元的分布式储能系统，能够储存光伏自用、剩余电量，与储能峰谷套利相结合，最大限度利用电能使储能系统协调达到最大效益的目的。

3.2 实验标准设定

“光伏+风电+储热”新能源储能系统的实际运行数据如表1 所示。

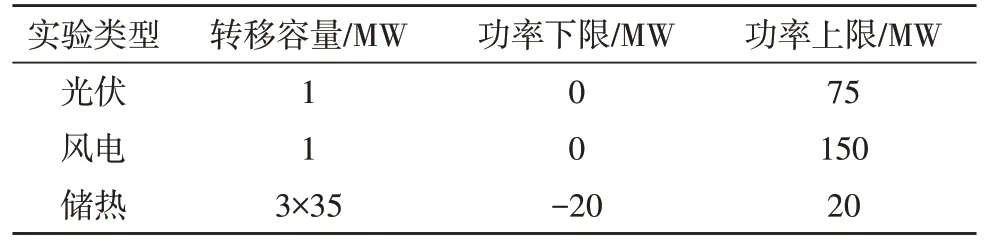
表1 实际运行数据

为了分析新能源储能系统协调优化模型的有效性，设置三种运行方式：

方式1：不考虑风电、储热运行耗能，且光伏运行能耗仅考虑固定运行方式；

方式2：不考虑光伏、储热运行耗能，且风电运行能耗仅考虑固定运行方式；

方式3：不考虑光伏、风电运行耗能，且储热运行能耗仅考虑固定运行方式。

在这三种运行方式下，功率越接近下限，说明系统整体耗能越少，也说明协调效果越好。

3.3 实验结果与分析

对于第一种运行方式，分别使用文献[1]模型、文献[2]模型和所构建模型对比分析光伏储能协调优化效果是否达到理想状态，如图4 所示。

由图4 可知，文献[1]模型在协调过程中超过了功率上限，且最高达到82 MW，经过80 s 协调后储能功率达到68 MW；文献[2]模型在协调过程中超过了功率上限，且最高达到85 MW，经过80 s 协调后储能功率达到63 MW；所构建模型在协调过程中没有超过功率上限，且最高达到80 MW，经过60 s 协调后储能功率稳定在43 MW。由此可知，所构建模型能够有效协调光伏储能系统。

对于第二种运行方式，分别使用不同模型对比分析风电储能协调效果是否达到理想状态，如图5所示。

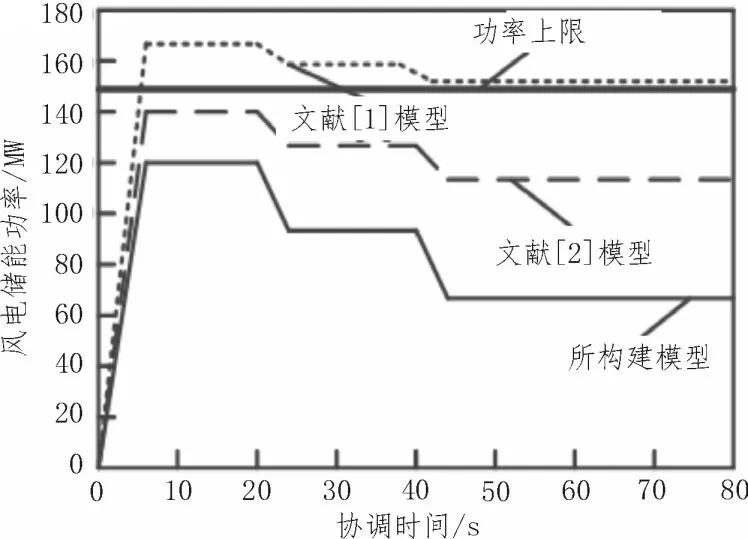
图5 不同模型风电储能协调效果对比分析

由图5 可知，三种方法协调曲线趋势一致，但所构建模型储能功率为65 MW，小于文献[1]模型和文献[2]模型，说明所构建模型能够有效协调风电储能系统。

对于第三种运行方式，分别使用不同模型对比分析储热协调效果是否达到理想状态，如图6 所示。

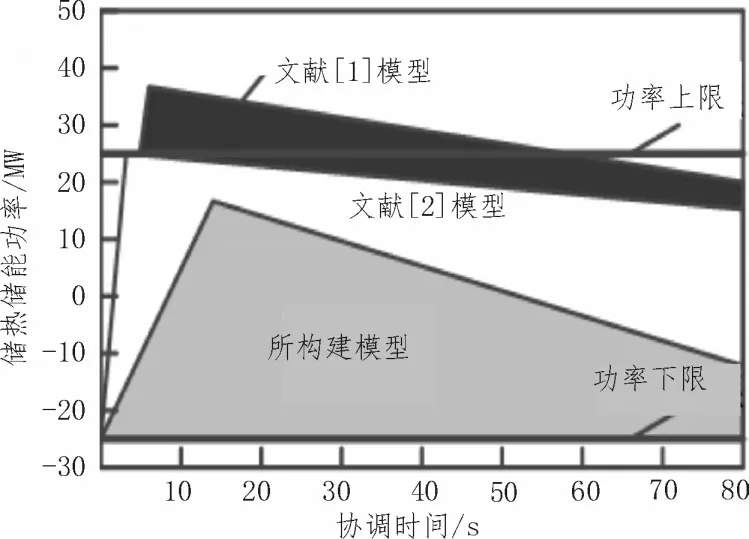
图6 不同模型储热储能协调效果对比分析

由图6 可知，文献[1]模型在整个协调过程中仍然超过了功率上限，文献[2]模型在协调过程中达到了功率上限，所构建模型储热储能功率为16 MW，低于功率上限，说明所构建模型能够有效协调储热储能系统。

综合上述分析可知，所构建模型具有较好的协调优化效果，有效促进了新能源并网消纳。

4 结束语

随着新能源储能系统一体化技术的快速发展，构建了改进NSGA-Ⅱ算法的新能源储能系统协调优化模型。将转移容量指标、负荷平衡指标作为约束条件，采用了改进的NSGA-Ⅱ算法对新能源储能系统进行了协调优化，该模型具有较好的协调优化效果，有效促进了新能源并网消纳，对实际应用具有一定指导意义。