激光雷达和视觉传感器组合系统的在线校准方法

朱蒙，马其华

（上海工程技术大学机械与汽车工程学院，上海 201620）

激光雷达和视觉传感器组合系统[1-2]因其超强的感知能力被广泛应用于自动驾驶领域[3]。传感器的检测准确性直接影响自动驾驶车辆的行车安全性[4]，传感器之间的相互校准[5-7]是保障其可靠性的重要手段之一。

在行车过程中采用的在线校准方法[8-10]，不需要辅助标记物，通过对目标对象的快速细化变换，实现及时检验并校准。文献[11]使用激光雷达反射图像进行校准，该方法需要大量场景数据，计算难度大。文献[12]并未使用所有激光雷达点的反射率信息，而是引入了两种使用深度信息的实时算法。在文献[12]的基础上，文献[13-14]设计了一个类似的校准系统。新颖之处在于边缘检测的数据预处理中，通过VICP 算法[15]对失真的激光雷达数据进行运动校正，以进一步提高精度。文献[16]发现估计激光雷达和图像边缘之间转换的鲁棒性至关重要，提出了一种低开销的稳健模型来评估稳定性。

为解决激光雷达和视觉传感器这一组合传感系统在工作状态下的在线校准问题，通过两个传感器测取同一目标物的点云与图像数据进行边缘匹配，确定是否存在传感器位置偏差的情况，并根据偏差情况采取不同的应急或校准方式进行处理。

1 原理与模型

设计激光雷达-视觉传感器组合系统的在线校准主要思路如下：

1）激光雷达和视觉传感器初始状态正常。根据KITTI 数据集中提供的传感器标准安装位置计算两传感器之间校准参数，作为初始标准值。

2）在车辆行驶的任意环境中随时间捕获一系列相应的激光点和相机图像，将激光点投影至相机图像，根据同一物体的激光雷达点和图像边缘的匹配原理，自动计算两传感器在此刻位置关系，得到校准参数。

3）将车辆行驶时得到的校准参数与初始标准值进行对比，判断两传感器相对位置是否发生变化并在车辆移动时通过调整偏移量来自动校正校准参数。

在线校准流程如图1 所示。

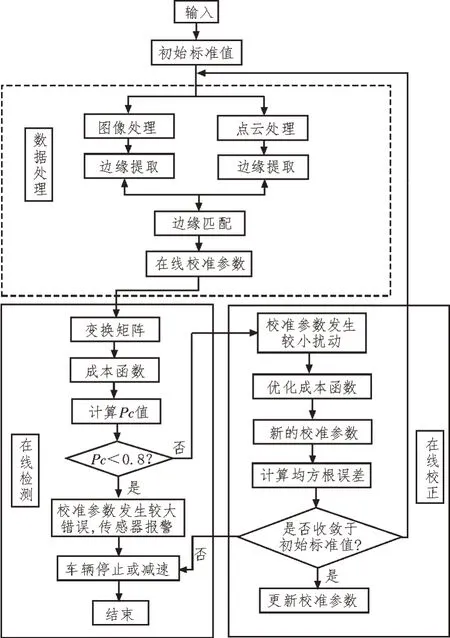
图1 在线校准流程

分别对激光雷达点云数据和视觉传感器输出的图像数据进行处理，获取边缘激光点和图像边缘，计算两传感器之间的校准参数。之后进行在线检测，根据边缘匹配得到的变换矩阵写为成本函数，利用成本函数计算Pc值（成本函数最差百分比），若0.8＞Pc＞0，则说明校准参数发生较大偏差，此时传感器做应急处理。若1＞Pc＞0.8，则校准参数发生较小扰动，此时进行在线校正，应用梯度下降法优化成本函数并不断获取新的校准参数。

1.1 视觉图像处理

对于图像传感器获得的在时间t内拍摄的n帧图像中的每一帧图像，都要进行灰度转换；应用边缘检测来生成边缘图像并输出，如图2 所示；利用逆距离变换使得当前图像帧的每个像素值Iu,v都获得一个到最近边缘像素的距离值。该距离值表示这是一条边的概率，使用归一化使距离值在0～1 内。

图2 边缘图像输出

Iu,v计算公式如下：

1.2 激光点云处理

由于原始激光点云数量大、杂乱无序、噪声多，需要对激光点云进行预处理。首先将激光雷达点投影到同一时刻的图像中，然后保留投影在图像中且可以找到的相同对象上的点，丢弃其他点。

对于光束的每个点Pi，相邻点是来自同一光束的左侧Pi-1点和右侧Pi+1点。点Pi的距离间隙值为：

其中，Ri是对应点Pi的坐标。根据KITTI 数据集的阈值设置，只提取间隙值Xi大于1 m 的点作为边缘点。

为了进一步改善边缘点的提取结果，应用中值滤波器去除随机噪声但保留清晰的特征。如图3 所示，使用RANSAC 线模型后，物体线条被清晰地提取出来，如电线杆、树干、铁轨的轮廓，并去除树点等轮廓。

图3 激光点云处理后提取的物体边缘点

1.3 校准参数评价指标

组合系统的输出结果为激光点云和图像的两者边缘，根据边缘匹配原理找到其3D 点云与2D 像素关系，通过矩阵变换计算在线校准参数。利用激光雷达坐标中的边缘3D 点云X=[x,y,z,1]T与2D 图像像素p=[u,v,1]T对应关系，计算其旋转矩阵R和平移向量T。转换矩阵计算公式如下：

其中，K是相机的固有参数，包括焦距(fu,fv)、原点(u0,v0) 。R[I/T]是具有平移T和旋转R的外在矩阵，其中，三个为平移参数，三个为旋转参数（统称校准参数）。

为了最大化成本函数，给定当前校准参数θ，在窗口大小为n的数据帧中，对于每一帧图像找到所有激光雷达边缘点。对于每个边缘点找到其对应的投影像素，使用双线性插值用于计算激光雷达点到图像像素投影过程中的值，即成本函数值。由于该函数不是凸函数，因此不可能全局搜索，即可能存在多个最优成本值。成本函数如下：

为解决成本函数可能存在多个最优值这一缺陷，添加一个约束以使用网格搜索方法验证校准参数的正确性。Pc的计算公式如下：

其中，∇θJ为每个数据的梯度，η是自适应步长。

由于校准参数越准确，成本函数值越大，因此，可用Pc（计算最差成本函数百分比），评估校准参数的正确性。由文献[12]可知，当Pc＜0.8，校准参数发生较大错误，1＞Pc＞0.8，校准参数发生较小扰动。

1.4 在线校正方法

对于校准参数发生较小扰动的参数，采用梯度下降法迭代优化成本函数，不断实时更新校准参数。假设成本函数在一个小的局部范围内是可微的，因不可能将图像值和点云范围直接写入成本函数，即它是通过数值梯度近似估计的。算法如下：

算法：梯度下降

2 结果与分析

实验使用KITTI 数据集进行测试，KITTI 数据集是利用组装的设备齐全的车辆对实际交通场景进行数据采集获得的公开数据集。该数据集包含丰富多样的传感器数据，有双目相机、64 线激光雷达、GPS/IMU 组合导航定位系统，基本满足对图像、点云和定位数据的需求，大量的标定真值包括检测2D 和3D包围框、跟踪轨迹等。该实验基于C++开发的机器人操作系统（ROS）、Ubuntu18.04，使用的库包括点云库（PCL）、OpenCV 等。

2.1 检测过程及分析

由上节可知，最差成本函数百分比Pc可用来判断参数是否发生偏差。通过对标准参数施加不同的位置偏移量验证其检验有效性，偏移量在[-10 cm,10 cm]或[-2°,2°]之间。结果如图4 所示。首先，算法在不到0.05 s 内快速响应；其次，当偏移量大于4 cm或偏移小于-6 cm 时，Pc＜0.8。偏移总量在10 cm 附近时，Pc值趋近稳定值1。由于平移偏移参数绝对值大于10 cm 时，算法检测其错误的 时间较长，因此，将平移偏移参数阈值设置为10 cm。

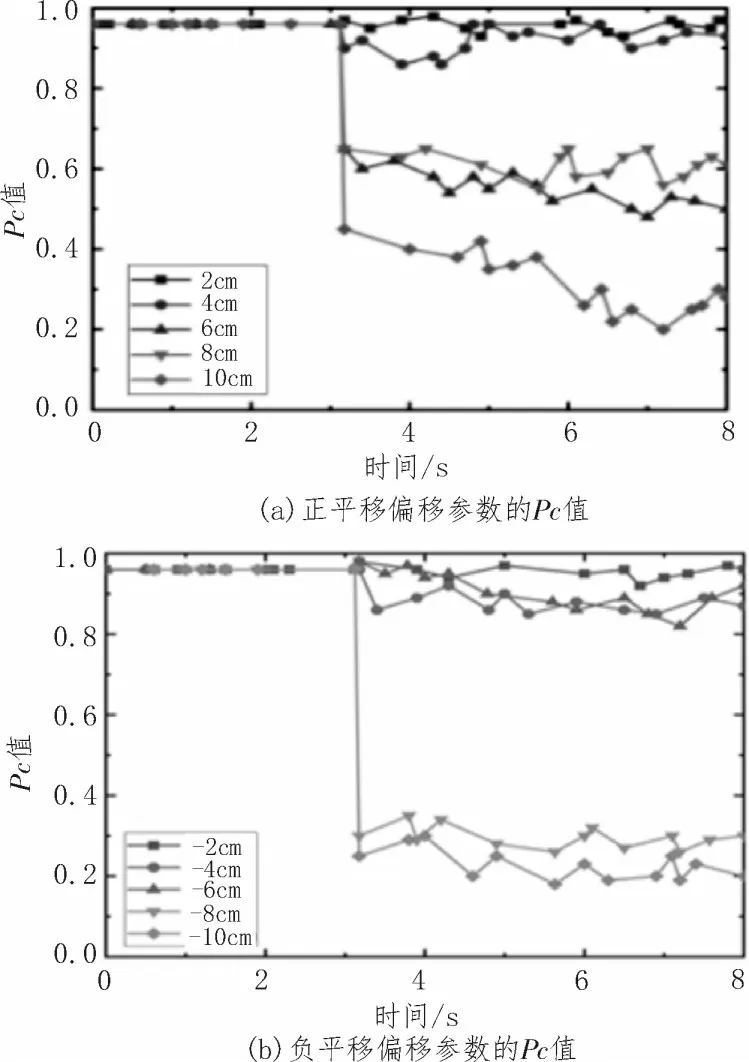
图4 初始标准参数偏移不同长度时的Pc值

对旋转角度偏移（Roll、Pitch、Yaw）从+2°至-2°进行试验，保持平移坐标不变，结果如图5 所示。首先，算法在不到0.05 s 内快速响应；其次，当旋转偏移大于+0.25°或小于-0.25°时，Pc＜0.8。Pc值稳定接近1 的区间约为0.5°。因此，算法可以检测到大于0.5°的旋转角度偏移。因旋转偏移绝对值大于2°时，算法检测其错误的时间较长，因此，将旋转偏移参数阈值设置为2°进行测试。

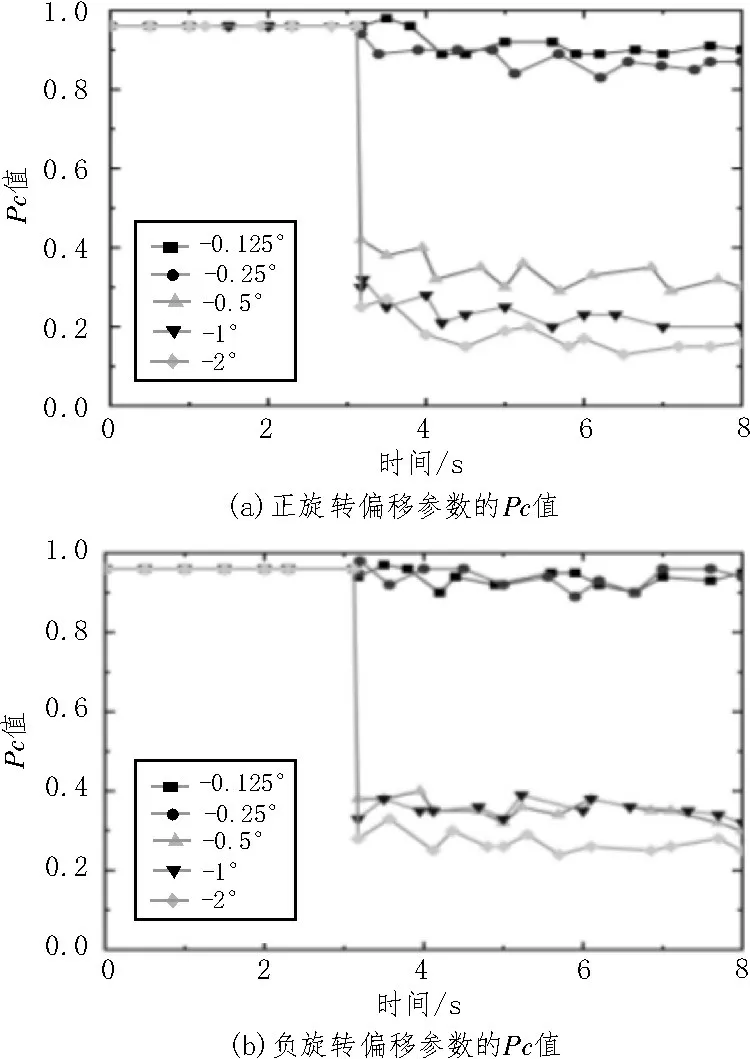
图5 初始标准参数旋转不同角度时的Pc值

2.2 校正过程及分析

由上节可知，在线检测算法可以在较短时间内检测出距离初始标准值大于10 cm 的平移偏移和大于0.5°的旋转偏移。而对于小于10 cm 和0.5°的校准参数，使用在线校正算法来修正参数。实验是通过改变初始标准值来完成的，设置平移偏移的范围为[-10 cm,10 cm]，间隔为2 cm，添加所有三个平移参数（X、Y、Z）上。对于修改旋转参数的实验，设置旋转偏移的范围为[-0.5°,0.5°]，被添加到所有三个旋转参数（Roll 水平、Pitch 俯仰、Yaw 偏航）上，如表1所示。

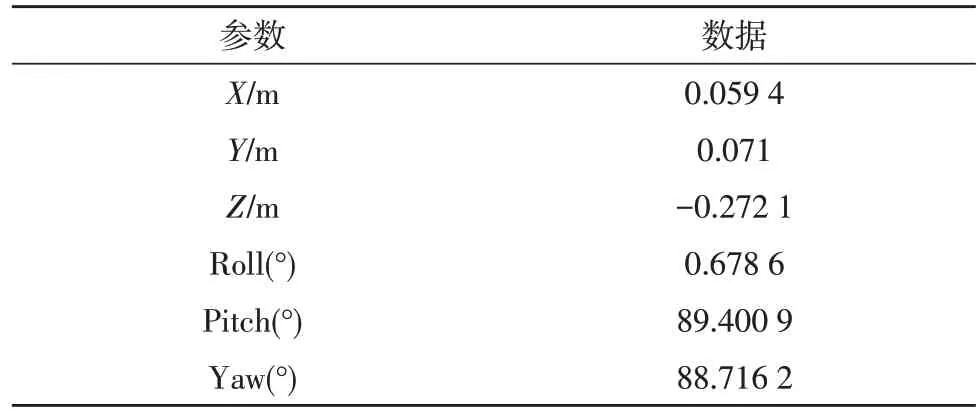
表1 初始标准参数

为验证算法的普遍适用性，进行了不同的平移和旋转实验。对于平移，表2 显示了从-10 cm 到10 cm 的不同初始平移偏移的校准参数在8 s 内更新的新校准参数。对于旋转，表3 显示了从-0.5°到0.5°的不同初始旋转偏移在8 s 内稳定的校准值。

表2 不同初始平移偏移参数更新后的稳定值

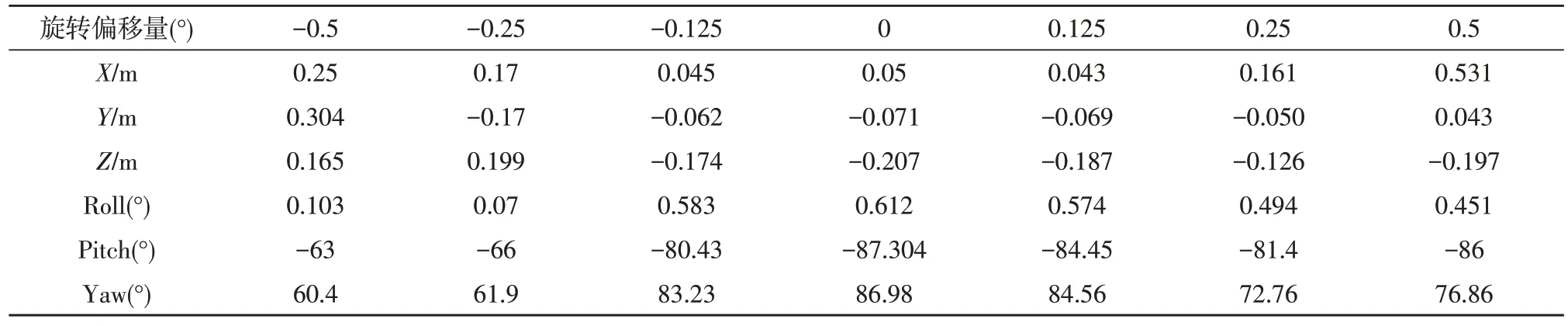
表3 不同初始旋转偏移参数更新后的稳定值

图6 显示了新校准参数的平移和旋转的RMSE（均方根误差）。由图6 可知，t=5.172 s 后，所有参数都处于稳定状态。平移偏移在[-4 cm,4 cm]以内，新校准参数的均方根误差小于0.08 cm，误差较小。平移偏移在[-4 cm,2 cm]之间，新校准参数的均方根误差为0.04 cm 左右，收敛于初始标准值。因此，该算法能够实现的平移校准范围为6 cm。

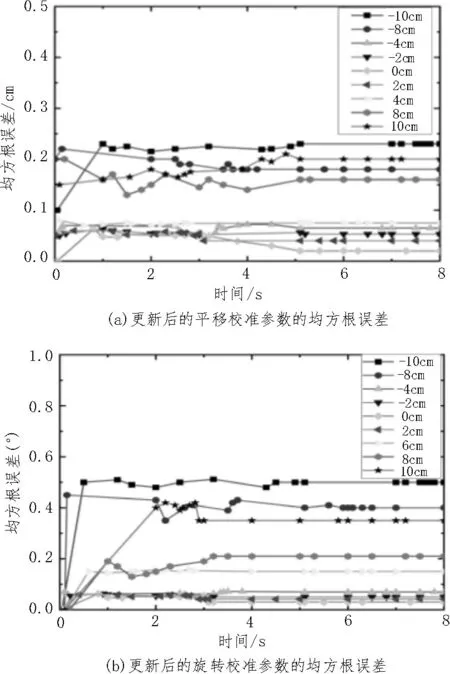
图6 不同平移偏移值参数的均方根误差

图7 显示了新校准参数的平移和旋转参数的均方根误差。更新后的校准参数在t=5.172 s 处稳定。考虑均方根误差，整体平移偏移均方根误差小于0.09 cm，整体旋转偏移误差为0.476°，对于[-0.125°,0.125°]的均方根误差，大约是0.05°。因此，该算法能校正的角度是0.25°。此外还测试了绝对值大于0.5°的旋转偏移，测试结果发现，旋转偏移大于0.5°，超出局部最优范围，算法无法更新校准参数，因为成本函数和Pc值无法保持高位。

图7 不同旋转偏移值参数的均方根误差

3 结论

基于激光点云和图像的边缘匹配原理自动计算校准参数，通过变换矩阵定义的成本函数进行校准参数检测，最后通过梯度下降法优化成本函数以不断获取新的校准参数，实现校准参数校正。因此，在传感器缓慢漂移或旋转的情况下，算法可以实时检测和校正变化，不仅不会中断车辆感知系统的正常运行，还可以显著提高车辆在未知恶劣环境中的灵活性和适用性。