基于ALO-BP 神经网络的SRAM 读时序预测

柴永剑，张立军，严雨灵，谢东东，马利军

（苏州大学轨道交通学院，江苏苏州 215000）

时序是芯片设计过程中需要考虑的最重要的性能指标之一，正确的时序关系是实现电路具体功能的基础。静态随机存取存储器（SRAM）作为SOC 芯片的重要组成部分，其性能对SOC芯片的影响很大[1]。因此，时序分析是SRAM 设计的重要流程[2]。

将电路图和对应版图抽取的RC 信息相结合，在不同工艺、电压、温度下对SRAM 进行模拟仿真，最终生成包含时序、功耗、泄漏等性能指标的liberty 文件。一套完整的SRAM 模拟仿真可能需要几百个小时。因此，需要对后仿真结果的时序值进行一定的预测。目前已有的研究主要是对前仿真时的标准单元库进行表征预测[3]，以及对一些典型的标准单元，如INV、AND、OR 等通过其晶体管的一些参数进行时序预测[4]；而对芯片后仿真结果中完整时序预测的研究较少。该文拟将BP 神经网络应用于后仿真读时序数据回归模型的建立，使用蚁狮算法优化网络的初始权值，将R2、绝对误差、均方误差等作为评估标准，结果显示该模型收敛速度较快，预测精度较高，具有良好的预测效果。

1 数据处理

1.1 数据描述与特征提取

SRAM 的时钟周期(Tcyc)主要受到读周期的影响，因此该文主要考虑读周期中的时序信息。芯片后仿真环节中通常采用关键路径(Critical Path,CP)的方法取代完整电路的仿真,以节省时间成本[5]。该文通过提取14 nm 单端口SRAM CP 电路的数据信息得到原始数据，采用的关键路径时序分析方法如图1所示。

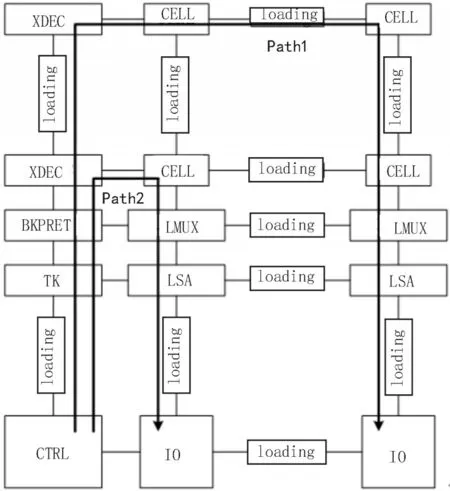
图1 SRAM关键路径时序分析方法

图1 中给出了该文SRAM 的基本结构，由存储单元阵列（Cell Array）、行地址译码器（XDEC）、字线延时追踪（TK）、灵敏放大器（SA）等组成。将存储阵列简化为4 个cell 单元，在电路基本连接信息正确的前提下，通过版图抽取的RC 信息将重复出现的电路单元以负载（loading）的形式替换。关键路径时序分析方法通常提供两种情况：最差路径Path1 和最优路径Path2，该文分析了最差路径Path1 的时序信息。

当存储器电路结构较为复杂时，采用分段拓展的方法计算存储器的延时，可利用公式计算得到相应的延时信息[6]。该文从后仿真生成的liberty 文件中的查找表(Look Up Table,LUT)提取了几种时序参数，具体内容如表1 所示。

表1 提取的读周期时间参数

由于芯片制造中不可避免的工艺偏差，同一芯片上不同位置的MOS 管性能会有所差异。针对新型制造工艺，采用统计学0CV—SOCV 模型进行补偿，生成该文采用的corner：FFG、SSG、TT[7]。此外，温度(T)、供电电压、存储容量参数、附加功能(F)等也会对SRAM 的读时序产生影响。该文提取了由上述参数构成的9 种数据特征及每组数据对应的时间参数值。每个时间参数均包含16 960 组数据，总共67 840 组数据。

1.2 特征预处理

1.2.1 特征量化

BP 神经网络的输入通常为数字信息，因而需要对采集到的数据特征中的文本信息进行量化,以保证模型的良好应用[8]。需要优化的特征如表2所示。

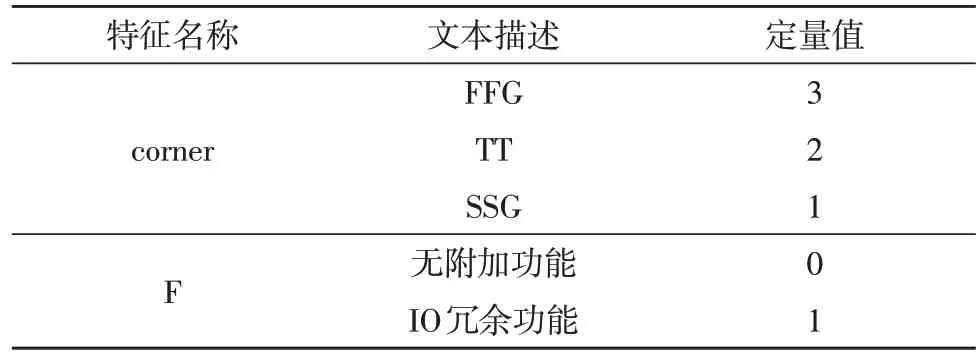
表2 特征的描述与量化

表2 中的每一个定量值代表该特征的不同状态，并作为BP 神经网络不同输入节点的特征值。

1.2.2 特征归一化

以特征量化完成后的Tcq部分数据为例，如图2所示。可以观察得到，温度的变化范围较大，在-40～125 间隔取值；而电路的字线、位线数则以2 的指数次幂增长式取值。

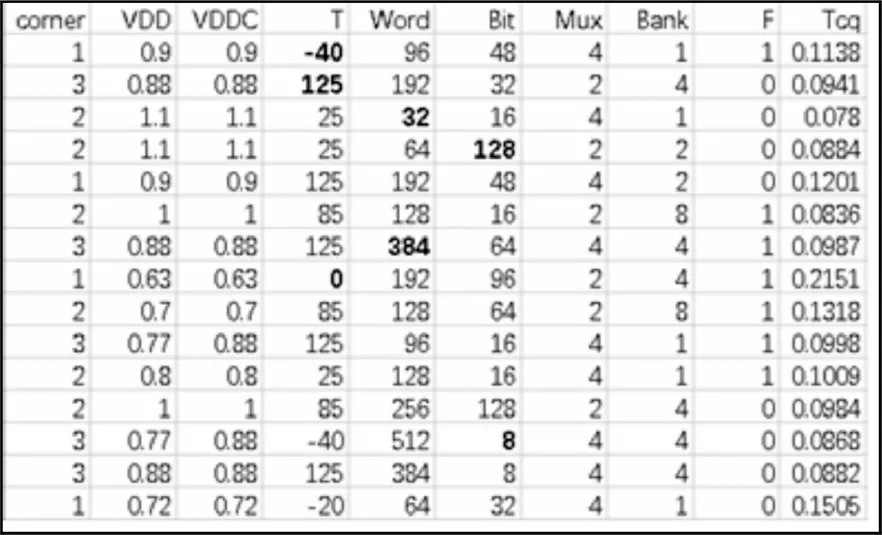
图2 处理后的部分Tcq数据

这类数量级较大的数据特征会对BP 网络的梯度更新产生影响，影响网络的收敛速度，因而需要对数据进行归一化处理。该文使用Min-Max 对时序数据进行归一化处理，变换函数如式（1）所示：

设计代码时，通过sklearn.preprocessing 库中的Min-Maxscaler 方法实现数据到[0,1]范围的等比缩放。处理完成后将数据按4∶1 的比例随机划分为训练集和测试集。

2 模型建立

2.1 BP神经网络

BP 神经网络是一种依据输出误差反向传播的前馈神经网络，被广泛应用到各个领域的预测研究中[9]。该文采用三层BP 神经网络，基本结构如图3所示。输入层节点数为9，即数据的9 种特征；隐含层节点数的选择将在下文实验中确定；输出层节点数为1，即时序预测输出值。

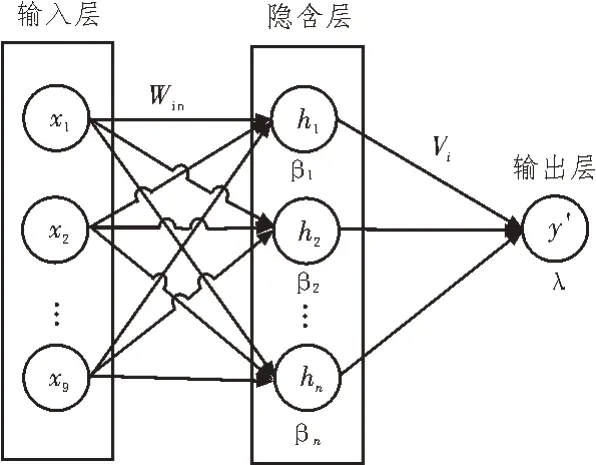
图3 三层BP神经网络的基本结构

该文用于特征转换的激活函数f均采用Sigmoid函数，具体表述为：

将预测样本的均方根误差作为模型的损失函数，若损失函数未达到理想要求则进行反向传播。寻找网络的最优权值，即要使损失函数取到极小值。该文对各参数的修正采用负梯度方向的最速下降法。

按各参数的修正值修改网络权值，使得输出误差信号最小。该文将BP 神经网络的学习率lr设置为0.5，在损失函数不震荡的前提下尽可能提高网络的收敛速度。

2.2 蚁狮优化算法

蚁狮优化(Ant Lion Optimizer,ALO)算法模拟自然界中蚁狮的狩猎机制，常用来对网络模型进行优化[10]。蚁狮在沙地中挖一个漏斗状的陷阱并藏在底部，等待随机游走的蚂蚁落入陷阱。蚁狮将其捕食后修理陷阱以备下一次捕猎。ALO算法的具体步骤如下：

1）确定蚂蚁和蚁狮的初始数量，对蚂蚁和蚁狮的初始位置进行随机处理：蚂蚁的随机游走根据式（3）的来确定：

式中，t表示随机游走的步数,tn为最大迭代次数，r(t)为一个随机函数。ai和bi分别表示第i维变量随机游走的最大值和最小值分别表示第i维变量在第t次迭代的最小值和最大值。

2）蚂蚁落入陷阱：蚂蚁随机游走的路线受陷阱影响，提出数学模型如下：

蚂蚁进入陷阱后，其随机游走的范围急剧下降，该过程可用式（5）-（6）模拟：

式中，I为比例，T=tn，w是一个常数。

3）当蚁狮适应度比蚂蚁大时，蚁狮将其捕获，更新蚁狮的位置：

式中，f为适应度函数。

4）每次迭代结束，选择适应度最好的蚁狮作为精英蚁狮。则第i只蚂蚁在第t+1 次迭代位置由精英蚁狮确定，如下：

2.3 ALO-BP模型参数设置

针对BP 神经网络在进行时序预测时收敛速度较慢，损失函数容易陷入局部极小值等问题，采用ALO 算法寻找神经网络的最优权值[11]，具体过程如图4 所示。为验证ALO-BP 算法对时序数据的预测效果，使用Python 语言进行模型搭建。种群数量Number=20，由BP 网络的各层数计算得到自变量个数dim=144，设定最大迭代次数Max_iteration=100。

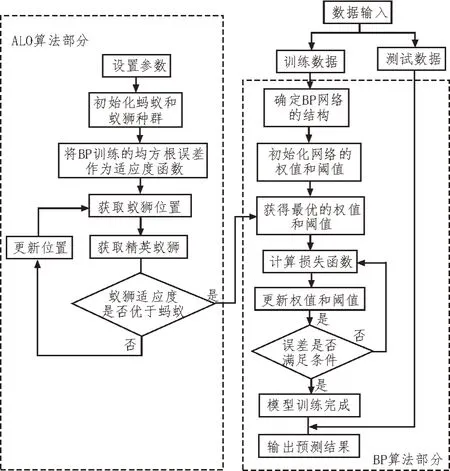
图4 ALO-BP模型实验流程图

BP 神经网络的迭代次数epochs=1 000，隐含层数量m根据经验公式（9）初步划定范围为[3,13]之间的整数。通过5 折交叉验证的方法[12]，计算出不同隐含层数的平均预测均方误差，当隐含层数为13 时，预测均方误差最小，即为该文的最佳隐含层数。

其中，n为输入节点数，l为输出节点数，b为[0,10]之间的整数。

3 实验结果分析

3.1 评价指标

为评估模型性能，选取平均绝对误差MAE、均方根误差RMSE 和绝对系数R2作为评价指标。需要注意的是在计算模型预测的绝对误差和均方根误差时对预测结果做反归一化处理，否则结果不够直观。绝对误差MAE能最直接地反应预测效果，如下：

采用均方根误差RMSE 评价预测的分布情况，值越小说明预测的数据结果越稳定[13]，如下：

采用决定系数R2评价回归模型拟合度[14]，如下：

其中，R2≤1，其值越大说明模型对数据的拟合度越好；R2＜0 时，表示模型无法对数据进行拟合。

3.2 模型预测结果分析

首先以时间参数Tcq的预测为例，初步评价该文模型的预测效果。ALO-BP 神经网络的训练过程如图5 所示。

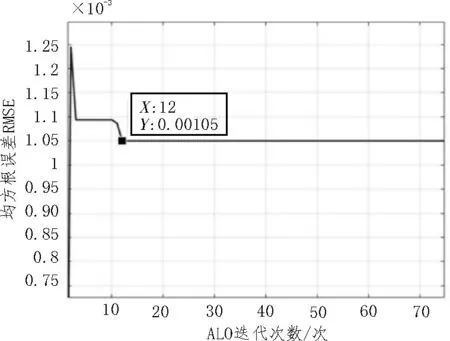
图5 ALO-BP模型对Tcq预测的迭代图

由图5 可知，BP 神经网络对测试数据的预测均方误差约为0.001 25，即ALO 算法适应度函数的初始值。该迭代过程的收敛速度较快，在第12 次迭代时就基本获得了适应度函数的极小值为0.001 05。通过学习过程优化神经网络的权值和阈值，最终得到该文模型对Tcq参数的预测效果。

从图6 中可以直观地看出ALO-BP 网络的预测效果较好，散点图显示该模型能够有效地对数据进行精确拟合。为了验证该文算法对时序数据预测的精确性，文中将K 近邻算法[15]、随机森林算法[16]、BP神经网络及基于ALO 的优化算法4 种方法的结果进行对比，Tcq的预测效果如表3 所示。

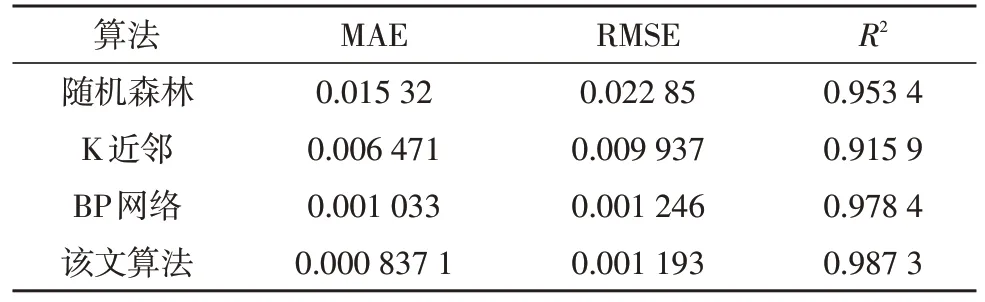
表3 4种算法对Tcq预测的评价指标对比

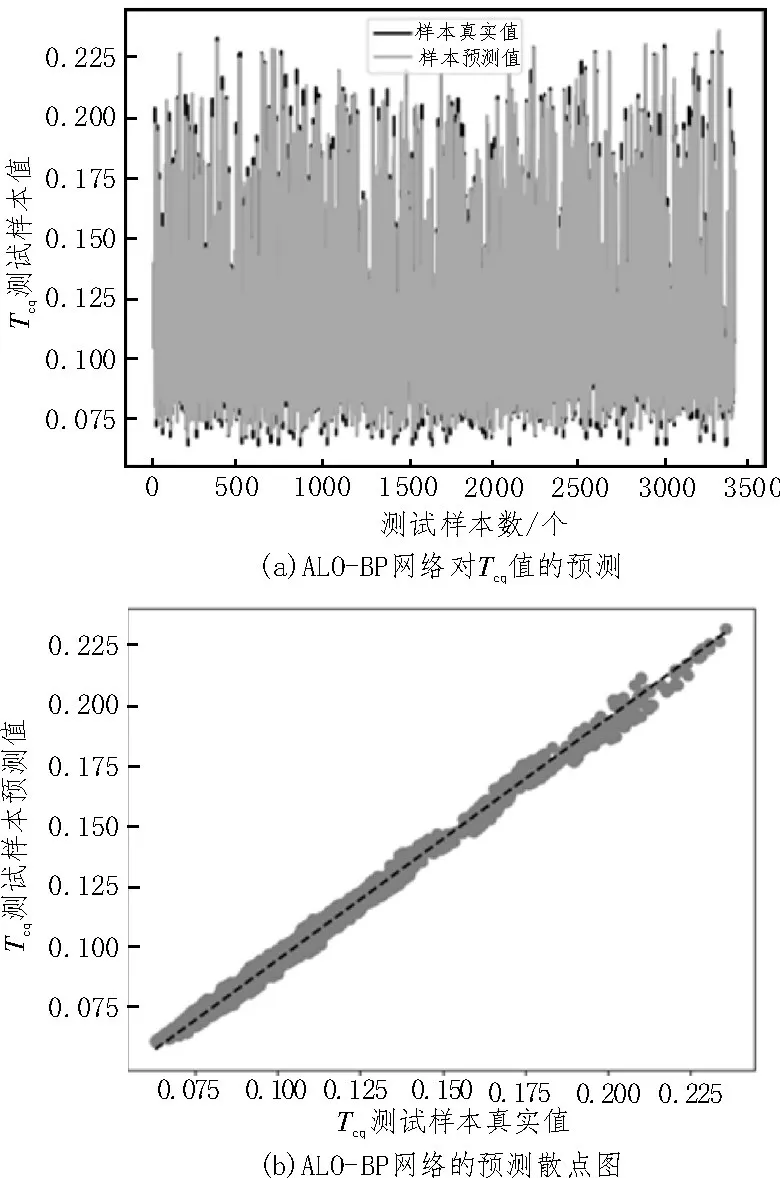
图6 ALO-BP模型的预测结果

该文需要预测的数据值数量级均在10-2～10-1之间，单位为ns，导致各个模型的绝对误差和均方根误差都偏小。通常要求SRAM 的时序误差不超过2 ps，因而只有BP 网络和该文算法的MAE 满足该精度要求。表3 中，随机森林算法对数据的拟合度较好，但预测误差偏大；相比之下，K 近邻算法减小了预测误差，但拟合度下降。BP 网络能在提高模型拟合度的同时进一步缩小预测误差，但受到网络初始权值和阈值的影响，其预测结果不够稳定。ALO-BP 算法很好地解决了上述其他方法的预测问题。

为进一步验证该文算法对其他时序数据的适应性，采用上述4 种方法对4 种时序参数进行了预测，模型拟合结果如表4 所示。

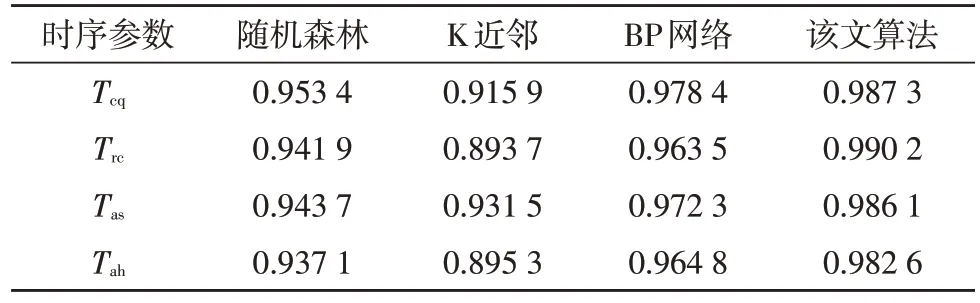
表4 不同时序数据的模型拟合度对比

表中数据显示，4 种方法对不同时序参数数据都能进行有效的拟合，其中K 近邻的拟合效果最差，BP网络的拟合效果不够稳定；而该文所采用的优化算法平均拟合度最高，能够对各种时序数据进行高精确度的预测。

4 结论

保证时序正确是设计芯片功能的重要前提。为了预测不同工艺角下的时序参数，该文提出了蚁狮优化BP 神经网络的时序预测模型，对较大数据量的不同时序参数值进行了较为准确地预测。通过测试结果和不同算法对比可以看出，该文模型对时序数据的拟合效果最好，模型平均拟合度可以达到0.98以上。