注塑级聚乳酸热分解动力学分析

罗越峰，温桦浩，廖正福

注塑级聚乳酸热分解动力学分析

罗越峰，温桦浩，廖正福*

（广东工业大学 材料与能源学院，广州 510006）

研究注塑级聚乳酸材料的热分解动力学，准确理解注塑级聚乳酸的耐热稳定性，为开发耐高温阻燃注塑级聚乳酸（PLA）材料提供理论依据。通过非等温热重分析法，采用5、10、15、20、25 ℃/min的升温速率，研究注塑级PLA在氮气气氛中的热分解行为，利用1种微分法和3种积分法进行详细的动力学计算。比较相关系数及标准偏差，选取KAS等温积分法，以相对偏差A=|1–c/e|为目标函数，利用16种热分解动力学机理模拟计算注塑级PLA热分解最合适的反应机理。得到了注塑级PLA热分解所需的活化能和指前因子，其中Kissinger、Madhusudanan-Krishnan-Ninan（MKN）、Kissinger-Akahira-Sunose（KAS）和Flynn-Wall-Ozawa（FWO）法计算所得注塑级PLA活化能分别为177.01、174.43、173.01和173.28 kJ/mol。指前因子分别为25.84、26.69～33.75、25.83～32.89和26.38～32.94。确定了随机成核和随后生长反应机理（A1/4），ln(/2)=ln[4.75×109/–ln(1–)]–2.08×104/是描述注塑级PLA热分解最合适的反应机理。

注塑级聚乳酸；热分解动力学；非等温分析；反应机理

注塑级聚乳酸（PLA）及其复合材料因其优异的透明度、生物相容性、生物降解性和可加工性已成为当今研究最为广泛的绿色塑料种类之一[1-4]，但是未改性注塑级PLA的热变形温度（HDT）只有58 ℃左右，远低于通用塑料PS和PP等[5]，使注塑级PLA的应用受到了很大限制。另外，改善PLA材料的热稳定性还可以改善其降解速率、成炭速率和出炭率等[6-7]，提高其阻燃性能。因此，研究注塑级PLA的热降解动力学，对准确研究其耐热机理，进而开发高耐热阻燃注塑级PLA材料，拓宽其应用具有重要意义。

目前为止，关于聚乳酸复合材料热解动力学的研究已有广泛报道[8-12]，但有关注塑级PLA热分解动力学的研究并不多，且不同PLA结构、分析方法和热失重气氛等研究结果也存在较大差异。氮气气氛中，金玉顺等[13]利用Freeman-Carroll、Achar和KAS法计算得到星形聚L-乳酸的热分解表观活化能值范围为128.61～134.79 kJ/mol，ln为23.46～25.28；付春华等[14]利用FWO和Friedman法计算得到D, L-聚乳酸热降解活化能值分别为97.78、90.64 kJ/mol；Alhulaybi等[15]利用Friedman、FWO、KAS和Starink法计算得到PLA热分解活化能值分别为97、109、104和104 kJ/mol。空气气氛中，韩宇辰等[16]利用FWO和Kissinger法求得反应活化能值分别为104.9、109.2 kJ/mol。通过Ozawa等失重百分率法求得热解反应的平均活化能值为91.4 kJ/mol和ln为14.9～18.2。本文拟通过非等温热重分析法，研究注塑级PLA在氮气气氛中的热分解行为，并通过Kissinger、FWO、KAS和MKN法进行热分解动力学分析，以期为注塑级PLA耐热稳定性研究提供一些参考依据。

1 实验

1.1 材料和仪器

主要材料和仪器：注塑级聚乳酸（PLA），3052D，美国Nature Works LLC；AL-204电子天平，METTLER TOLEDO；DZF-6020真空干燥箱，上海博迅实业有限公司医疗设备厂；SDT-2960热重分析仪，美国TA公司。

1.2 表征方法

热失重曲线在美国TA公司SDT-2960热重分析仪上记录，扫描温度为室温～800 ℃，N2气氛，流速为20 mL/min，升温速率分别为5、10、15、20、25 ℃/min。

1.3 PLA热分解动力学简析

研究物质热解机理的热分析方法分为等温动力学方法和非等温动力学方法。其中，非等温动力学又分为无模型动力学方法和模型拟合动力学方法[17]。无模型方法是材料热解过程动力学研究中最常用的方法[18-23]，也称为等转换法。无模型方法分为微分法和积分法2类，微分法由于采用瞬时速率值、差分等变换方法，对实验噪声敏感，往往使得计算数值不稳定，而积分法可以有效避免这种现象[24]。热重分析（TGA）方法简单、准确，是获得热解特性和动力学参数的最佳方法[25-29]。

固体的热分解过程是一种非均相的热分解反应体系，一般可描述为：

固体（solid）→最终分解残留物（solid）+挥发物（gas）

定义热解失重转化率为：

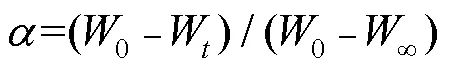
(2)

式中：为指前因子，s−1；为表观活化能，kJ/mol；为气体常数，=8.314 J/(mol·K)；为绝对温度，K。非均相固体热分解反应的分解速率定义如下：

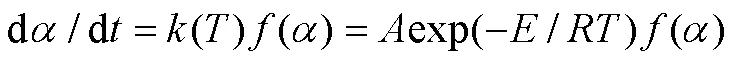
对样品线性升温时，升温速率dd，则式（3）变为：

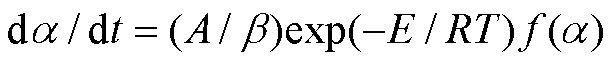
式（3）和式（4）是基于物质热失重数据进行热分解动力学分析的2个基本微分方程。热分解动力学研究的任务就是设法获得式（3）和式（4）中表征某个热解反应过程的动力学三因子：()，并以此来对热分解曲线进行拟合和预测，进而展开热分解过程的模拟设计与参数控制。

1.4 微分动力学参数计算

1.4.1 Friedman等转化率微分法

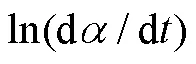
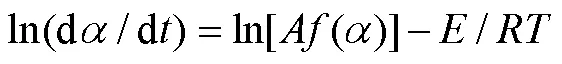
1.4.2 Kissinger等转化率微分法

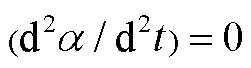
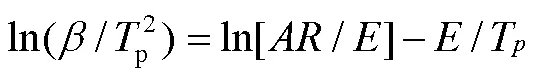
1.5 积分动力学参数计算

1.5.1 MKN等温积分法

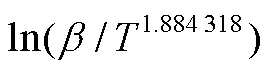
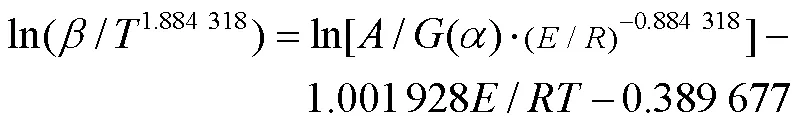
1.5.2 KAS等温积分法

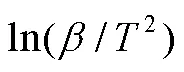
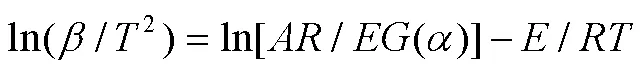
1.5.3 FWO等温积分法

Flynn-Wall-Ozawa（FWO）方法基于阿伦尼乌斯定律和Doyle的近似理论[38]，是等转换热分析方法中常用的积分方法之一[39-40]（式（9））。通过lg对1/作图，由斜率可计算值，由截距和机理函数()可求得ln值。

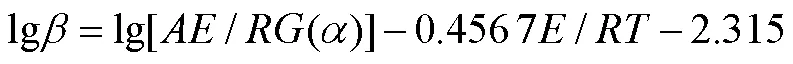
2 结果与分析

2.1 PLA的热失重分析

图1为PLA在不同升温速率下的TG-DTG曲线。可以发现，PLA仅有一段热失重（320～390 ℃）。温度低于320 ℃时，TG曲线平直，表明PLA没有发生热分解。在320～390 ℃，TG曲线斜率骤变，PLA发生热分解，样品热失重迅速。随着温度的继续增加，当温度达到390 ℃以上，PLA热分解基本结束，样品不再质量损失，最大质量损失率达到97%以上。随着升温速率从5 ℃/min增加到25 ℃/min，PLA热解温度（）也随之增加（见表1），表明PLA热解温度与升温速率有关。原因在于热解速率滞后于升温速率，需要较高温度加以补偿。

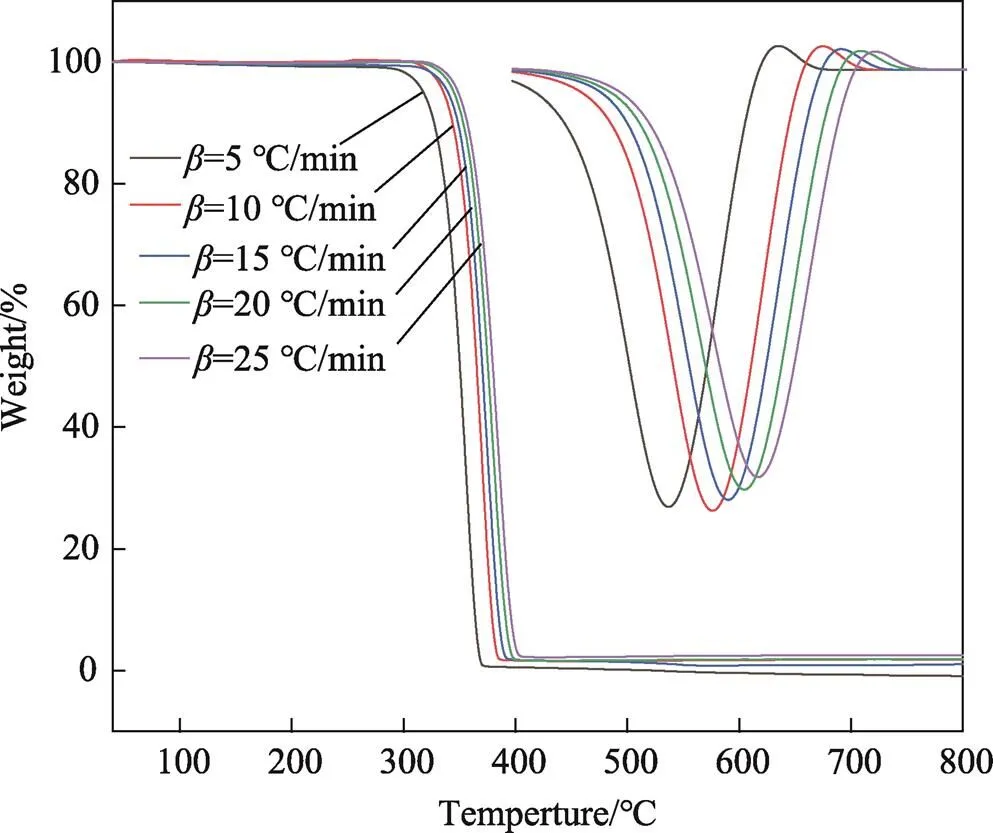
图1 TG-DTG曲线

表1 不同升温速率下热解参数

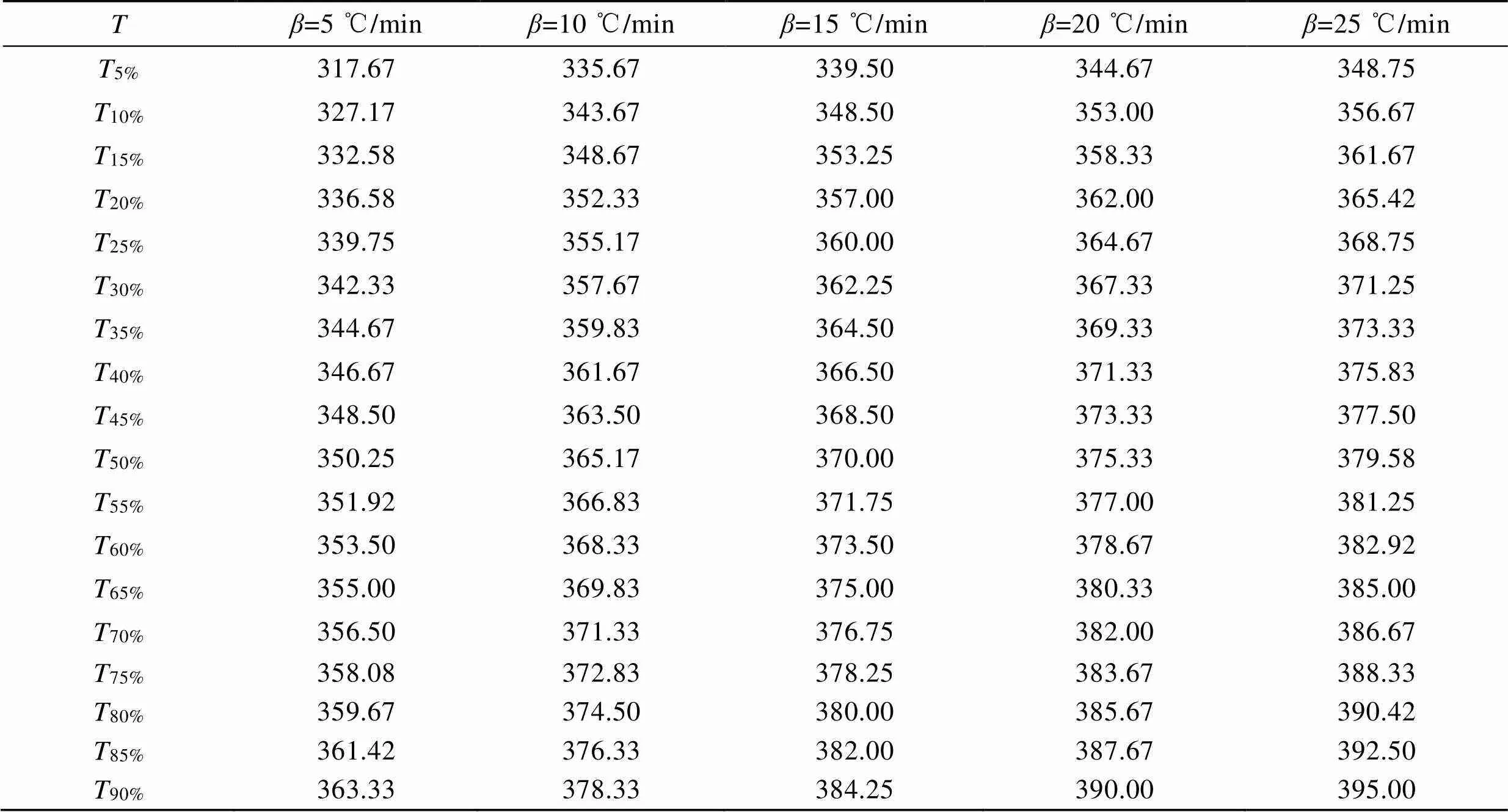
Tab.1 Thermal deposition parameters at different heating rates

2.2 PLA的热分解活化能计算

为了更好地理解PLA的热分解过程，分别利用Kissinger、MKN、KAS和FWO法，对表1热解参数进行线性拟合得到等转化率Arrhenius图（图2a～d）。根据直线斜率，可分别求得PLA的热分解活化能（见表2）。可以发现，用MKN、KAS、FWO方法计算得到的活化能并非常数，随转化率变化。在整个热失重区间，MKN方法求得介于148.81～179.03 kJ/mol，平均值为173.28 kJ/mol；KAS方法求得介于148.51～178.76 kJ/mol，平均值为173.01 kJ/mol；FWO方法求得介于150.69～180.02 kJ/mol，平均值为174.43 kJ/mol；Kissinger方法求得的平均值为177.01 kJ/mol。比较4种方法，MKN、KAS、FWO方法计算得到的活化能平均值相近，而Kissinger法由于只采样一个温度点而得到的活化能偏大。同时，MKN方法的R介于0.955 0～ 0.993 0，平均值为0.981 7；KAS方法的2介于0.954 7～0.992 9，平均值为0.981 6；FWO方法的2介于0.959 9～0.993 7，平均值为0.983 5；Kissinger方法的2为0.988 8。4种方法模拟所得线性相关系数R均接近于1，表明数据间线性关系优良，4种方法计算均具有良好的准确性，所得活化能结果是可靠的。

指前因子ln是物质热分解过程的另一个重要动力学参数。从图2a～d的直线截距可以计算PLA热分解过程的ln（如表2所示）。其中，MKN方法得到的PLA的ln介于26.69～33.75，平均值为32.44；KAS方法得到的PLA的ln介于25.83～32.89，平均值为31.58；FWO方法得到的PLA的ln介于26.38～33.18，平均值为31.92；Kissinger方法求得的ln为32.75。4种方法计算所得PLA的指前因子均相近，同时MKN、KAS和FWO法所得的活化能和指前因子值随着变化的趋势是一致的，这与文献[16, 41]的报道是一致的，进一步证实上述活化能计算结果的可靠性。

上述结果表明，Friedman法受基线漂移的干扰影响非常显著，往往导致计算数据不够准确；Kissinger法由于只采样一个温度点而得到的活化能偏大，不够准确；FWO和MKN法在=50%前受挥发性物质分解的影响较大，2平均值均小于KAS法，不够准确。为此，选用相对准确、简单的KAS法进行PLA的热分解反应机理的确定。

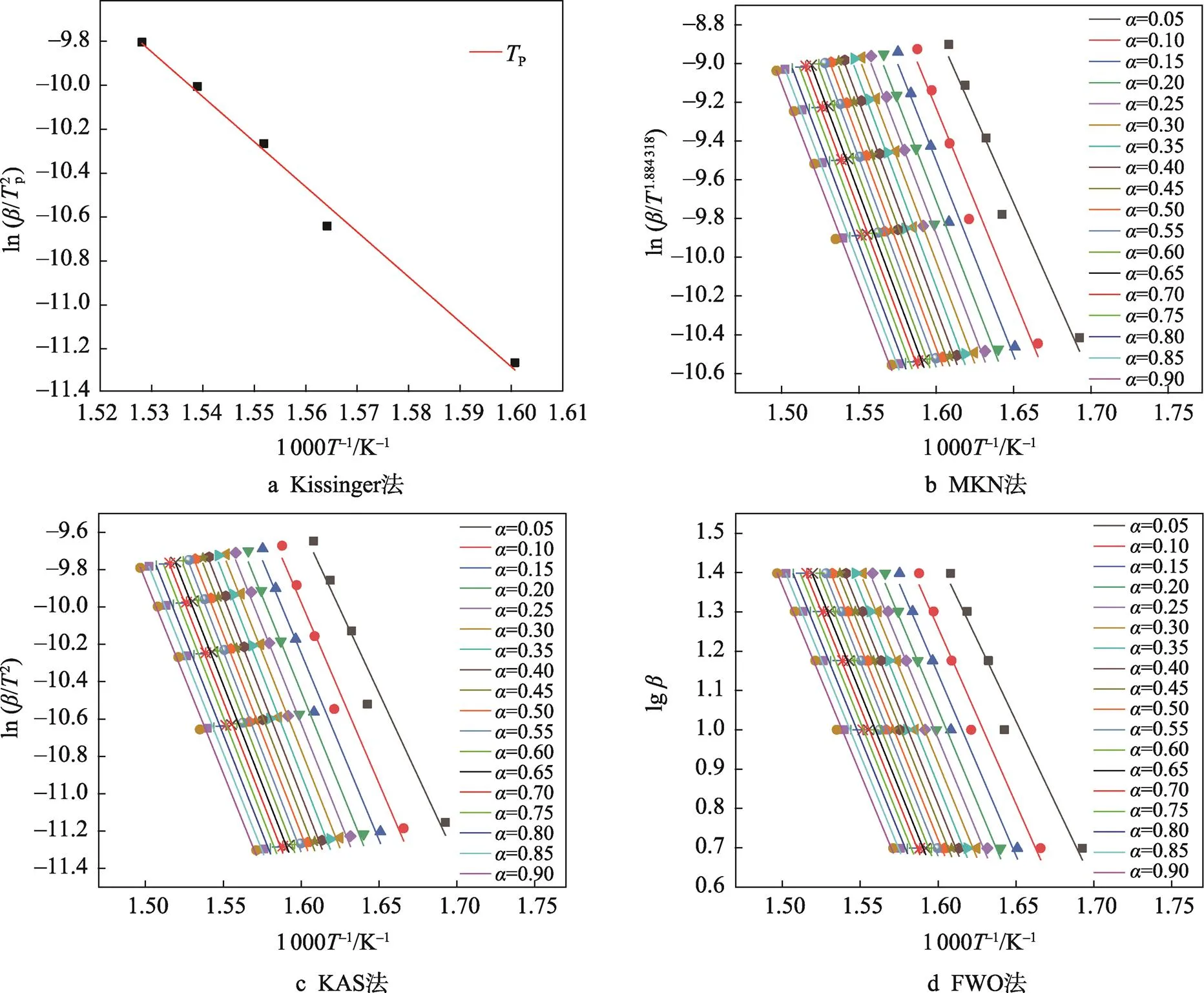
图2 等转化率Arrhenius图

表2 FWO、KAS、MKN和Kissinger法拟合计算的结果

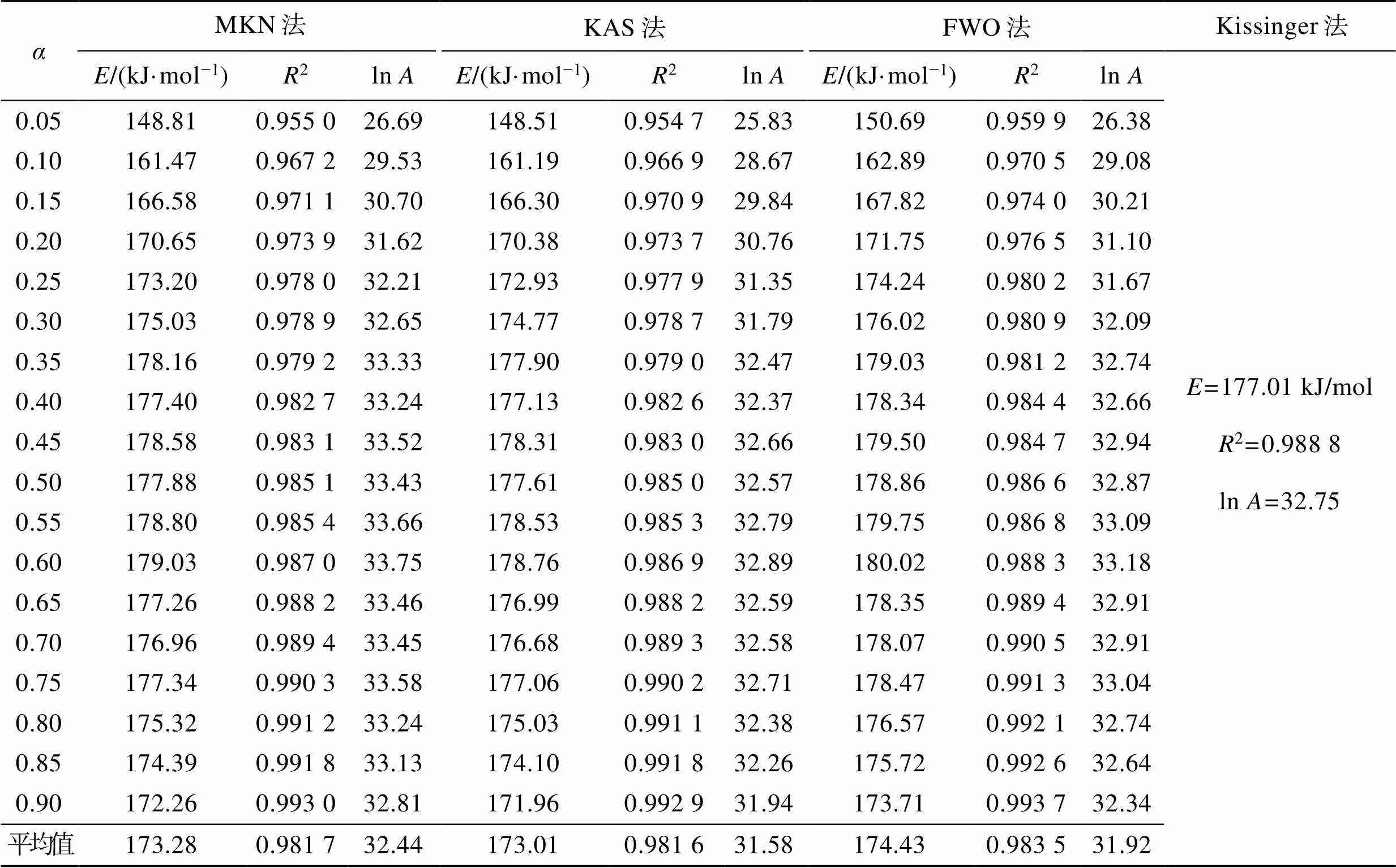
Tab.2 Results of the fitting calculations by the FWO, KAS, MKN and Kissinger methods

2.3 PLA的热分解反应机理的确定

表3 16种机理函数的微分和积分形式

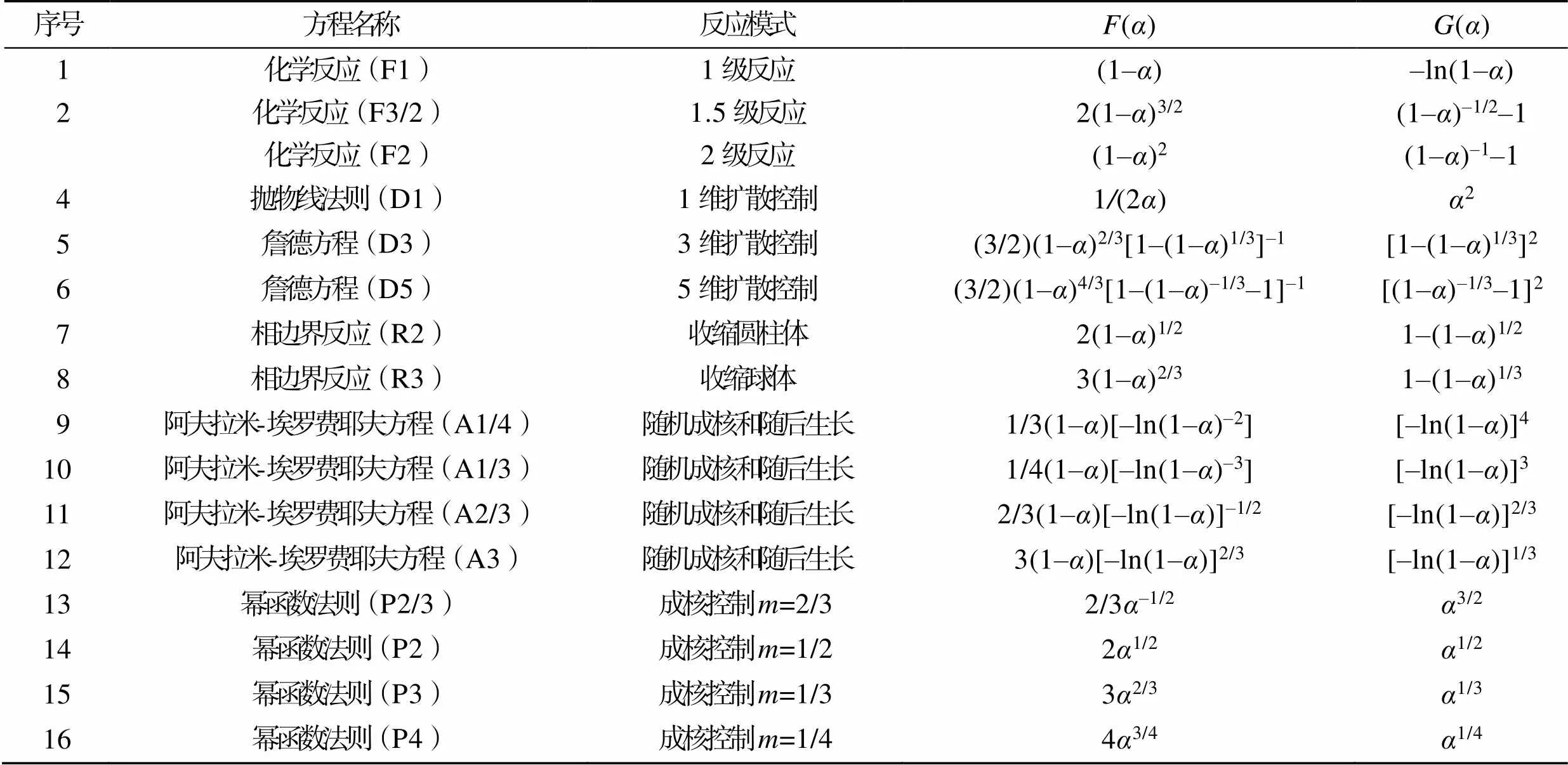
Tab.3 Differential and integral forms of 16 mechanism functions

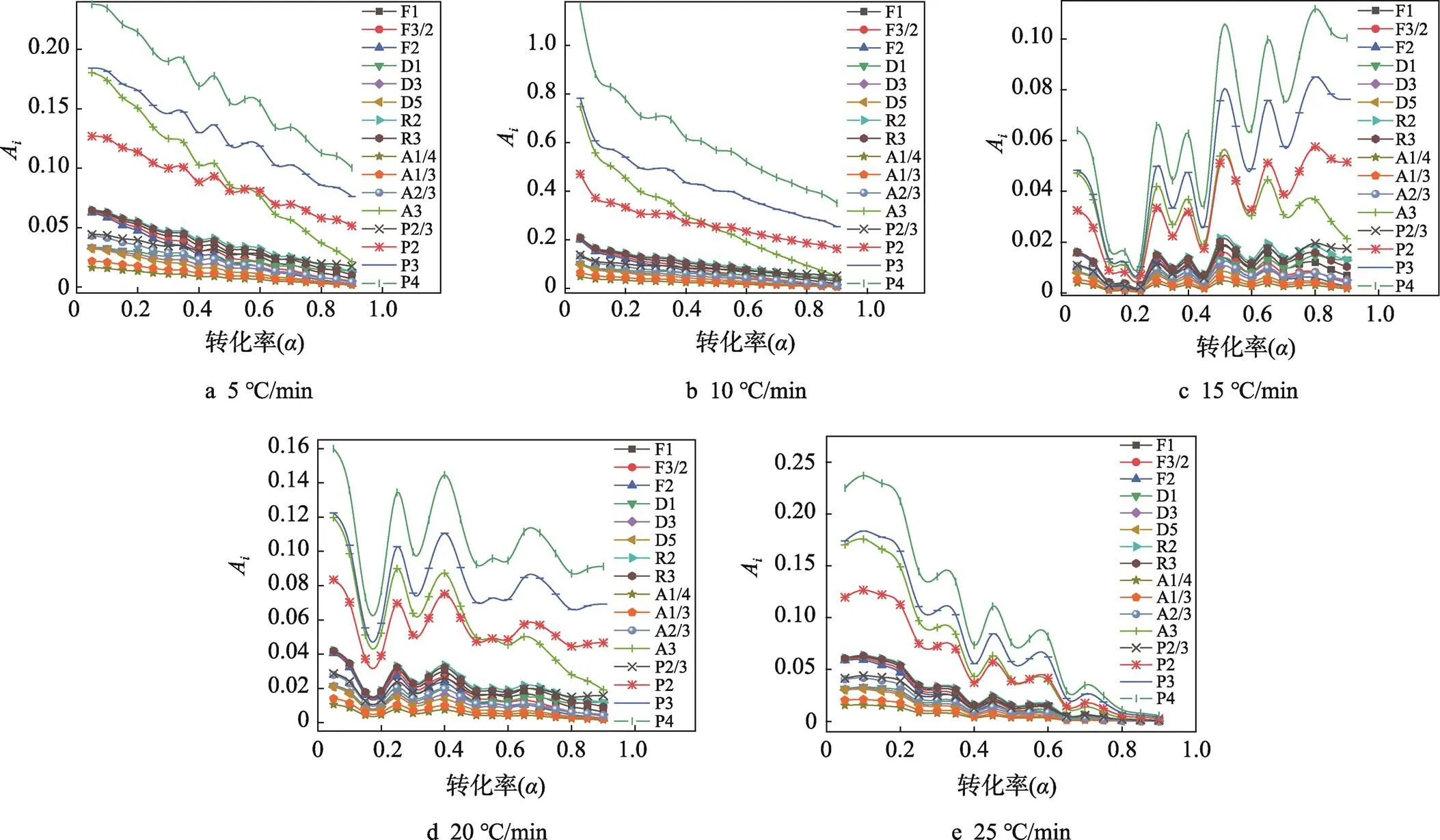
图3 PLA反应机理模拟

3 结语

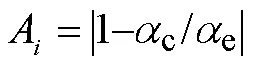
1）MKN、KAS、FWO和Kissinger 4种方法模拟所得线性相关系数2均接近于1，表明数据间线性关系优良，4种方法计算均具有良好的准确性，所得活化能结果是可靠的。

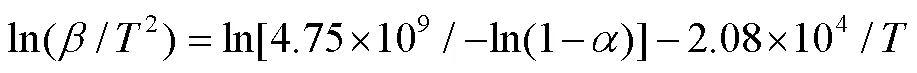
因本文重点在于研究注塑级PLA材料的热分解动力学，用于准确理解注塑级PLA的耐热稳定性，为开发耐高温阻燃注塑级PLA材料提供理论依据。为此关于机理的合理性，正在进一步实验验证。

[1] CASTRO-AGUIRRE E, IÑIGUEZ-FRANCO F, SAMSUDIN H, et al. Poly(lactic acid)-Mass Production, Processing, Industrial Applications, and End of Life[J]. Advanced Drug Delivery Reviews, 2016, 107: 333-366.

[2] BENVENUTA-TAPIA J J, VIVALDO-LIMA E. Reduction of Molar Mass Loss and Enhancement of Thermal and Rheological Properties of Recycled Poly(Lactic Acid) by Using Chain Extenders Obtained from RAFT Chemistry[J]. Reactive and Functional Polymers, 2020, 153: 1381-5148.

[3] RANAKOTI L, GANGIL B, BHANDARI P, et al. Promising Role of Polylactic Acid as an Ingenious Biomaterial in Scaffolds, Drug Delivery, Tissue Engineering, and Medical Implants: Research Developments, and Prospective Applications[J]. Molecules, 2023, 28(2): 485.

[4] LIU S, QIN S, HE M, et al. Current Applications of Poly(Lactic Acid) Composites in Tissue Engineering and Drug Delivery[J]. Composites Part B: Engineering, 2020, 199: 1359-8368.

[5] 郭彦彬. 耐热级生物降解塑料聚乳酸的研究[D]. 镇江: 江苏科技大学, 2012.

GUO Y B. Study on Thermostable Biodegradable Plastic Polylactic Acid[D]. Zhenjiang: Jiangsu University of Science and Technology, 2012.

[6] CHEN Y, WANG Q. Thermal Oxidative Degradation Kinetics of Flame-Retarded Polypropylene with Intumescent Flame-Retardant Master Batches in Situ Prepared in Twin-Screw Extruder[J]. Polymer Degradation and Stability, 2007, 92(2): 280-291.

[7] CHEN Y, LIU Y, WANG Q, et al. Performance of Intumescent Flame Retardant Master Batch Synthesized Through Twin-Screw Reactively Extruding Technology: Effect of Component Ratio[J]. Polymer Degradation and Stability, 2003, 81(2): 215-224.

[8] 桑练勇, 晏华, 代军, 等. 聚碳酸亚丙酯与聚乳酸共混物性能及热分解动力学分析[J]. 中国塑料, 2017, 31(12): 39-45.

SANG L Y, YAN H, DAI J, et al. Properties and Thermal Decomposition Kinetics of Poly(propylene carbonate) and Poly(lactic acid) Blends[J]. China Plastics, 2017, 31(12): 39-45.

[9] CAO Y, CHEN Z H, BOUKHIR M, et al. Insight into the Pyrolysis of Bamboo Flour, Polylactic Acid and Their Composite: Pyrolysis Behavior, Kinetic Triplets, and Thermodynamic Parameters Based on Fraser-Suzuki Deconvolution Procedure[J]. Bioresource Technology, 2024, 391(Pt A): 129932.

[10] TAI H S, CHEN C Y. Kinetic Study of Copyrolysis of Waste Polyethylene Terephthalate, Polylactic Acid, and Rice Straw[J]. Environmental Engineering Science, 2016, 33(9): 671-680.

[11] WANG G, LI A. Thermal Decomposition and Kinetics of Mixtures of Polylactic Acid and Biomass during Copyrolysis[J]. Chinese Journal of Chemical Engineering, 2008, 16(6): 929-933.

[12] MONIKA, DHAR P, KATIYAR V. Thermal Degradation Kinetics of Polylactic Acid/Acid Fabricated Cellulose Nanocrystal Based Bionanocomposites[J]. International Journal of Biological Macromolecules, 2017, 104: 827-836.

[13] 金玉顺, 郭文莉, 李树新, 等. 星形聚L-乳酸的热分解动力学研究[J]. 现代化工, 2009, 29(S2): 175-177.

JIN Y S, GUO W L, LI S X, et al. Kinetic Study on Thermal Degradation of Star Shaped Poly(L-Lactide)[J]. Modern Chemical Industry, 2009, 29(S2): 175-177.

[14] 付春华, 李永刚, 罗彦凤, 等. D, L-聚乳酸热降解动力学研究[J]. 包装工程, 2007, 28(5): 7-9.

FU C H, LI Y G, LUO Y F, et al. Thermal Degradation Kinetics of Biodegradable D, L-Polylactic Acid[J]. Packaging Engineering, 2007, 28(5): 7-9.

[15] ALHULAYBI Z, DUBDUB I, AL-YAARI M, et al. Pyrolysis Kinetic Study of Polylactic Acid[J]. Polymers (Basel), 2022, 15(1): 12.

[16] 韩宇辰, 黄震, 冯梅, 等. 可降解聚乳酸的热分解动力学研究[J]. 包装工程, 2012, 33(19): 75-78.

HAN Y C, HUANG Z, FENG M, et al. Study on Thermal Decomposition Kinetics of Biodegradable Poly Lactic Acid[J]. Packaging Engineering, 2012, 33(19): 75-78.

[17] LAH B, KLINAR D, LIKOZAR B. Pyrolysis of Natural, Butadiene, Styrene-Butadiene Rubber and Tyre Components: Modelling Kinetics and Transport Phenomena at Different Heating Rates and Formulations[J]. Chemical Engineering Science, 2013, 87: 1-13.

[18] JIANG Z, LIU Z, FEI B, et al. The pyrolysis characteristics of moso bamboo[J]. Journal of Analytical & Applied Pyrolysis, 2012, 94: 48-52.

[19] ZHAO H, YAN H X, DONG S S, et al. Thermogravimetry Study of the Pyrolytic Characteristics and Kinetics of Macro-Algae Macrocystis Pyrifera Residue[J]. Journal of Thermal Analysis and Calorimetry, 2013, 111(3): 1685-1690.

[20] AGRAWAL A, CHAKRABORTY S. A Kinetic Study of Pyrolysis and Combustion of Microalgae Chlorella Vulgaris Using Thermo-Gravimetric Analysis[J]. Bioresource Technology, 2013, 128: 72-80.

[21] WONGSIRIAMNUAY T, TIPPAYAWONG N. Thermogravimetric Analysis of Giant Sensitive Plants under Air Atmosphere[J]. Bioresource Technology, 2010, 101(23): 9314-9320.

[22] ABOULKAS A, EL HARFI K, EL BOUADILI A. Non-Isothermal Kinetic Studies on Co-Processing of Olive Residue and Polypropylene[J]. Energy Conversion and Management, 2008, 49(12): 3666-3671.

[23] ÇEPELIOĞULLAR Ö, PÜTÜN A E. Thermal and Kinetic Behaviors of Biomass and Plastic Wastes in Co-Pyrolysis[J]. Energy Conversion and Management, 2013, 75: 263-270.

[24] VYAZOVKIN S, BURNHAM A K, CRIADO J M, et al. ICTAC Kinetics Committee Recommendations for Performing Kinetic Computations on Thermal Analysis Data[J]. Thermochimica Acta, 2011, 520(1/2): 1-19.

[25] LIU J B, JIANG X Y, CAI H Z, et al. Study of Combustion Characteristics and Kinetics of Agriculture Briquette Using Thermogravimetric Analysis[J]. ACS Omega, 2021, 6(24): 15827-15833.

[26] MADHU G, MANDAL D K, BHUNIA H, et al. Thermal Degradation Kinetics and Lifetime of High-Density Polyethylene/Poly (l-Lactic Acid) Blends[J]. Journal of Thermoplastic Composite Materials, 2017, 30(6): 773-793.

[27] YUANYUAN Z, YANXIA G, FANGQIN C, et al. Investigation of Combustion Characteristics and Kinetics of Coal Gangue with Different Feedstock Properties by Thermogravimetric Analysis[J]. Thermochimica Acta, 2015, 614: 137-148.

[28] ZHOU Z, HU X, YOU Z, et al. Oxy-Fuel Combustion Characteristics and Kinetic Parameters of Lignite Coal from Thermo-Gravimetric Data[J]. Thermochimica Acta, 2013, 553: 54-59.

[29] MA Z, CHEN D, GU J, et al. Determination of Pyrolysis Characteristics and Kinetics of Palm Kernel Shell Using TGA-FTIR and Model-Free Integral Methods[J]. Energy Conversion and Management, 2015, 89: 251-259.

[30] CRAPSE J, PAPPIREDDI N, GUPTA M, et al. Evaluating the Arrhenius Equation for Developmental Processes[J]. Molecular Systems Biology, 2021, 17(8): 9895.

[31] FRIEDMAN H L. Kinetics of Thermal Degradation of Char-Forming Plastics from Thermogravimetry[J]. Application to a phenolic plastic[J]. Journal of Polymer Science Part C: Polymer Symposia, 1964, 6(1): 183-195.

[32] SBIRRAZZUOLI N. Is the Friedman Method Applicable to Transformations with Temperature Dependent Reaction Heat?[J]. Macromolecular Chemistry and Physics, 2007, 208(14): 1592-1597.

[33] BROWN M E, MACIEJEWSKI M, VYAZOVKIN S, et al. Computational Aspects of Kinetic Analysis: Part A: The ICTAC Kinetics Project-Data, Methods and Results[J]. Thermochimica Acta, 2000, 355(1): 125-143.

[34] KISSINGER H E. Reaction Kinetics in Differential Thermal Analysis[J]. Analytical Chemistry, 1957, 29(11): 1702-1706.

[35] MADHUSUDANAN P M, KRISHNAN K, NINAN K N. New Approximation for the() Function in the Evaluation of Non-Isothermal Kinetic Data[J]. Thermochimica Acta, 1986, 97: 189-201.

[36] MADHUSUDANAN P M, KRISHNAN K, NINAN K N. New Equations for Kinetic Analysis of Non-Isothermal Reactions[J]. Thermochimica Acta, 1993, 221(1): 13-21.

[37] COATS A W, REDFERN J P. Kinetic Parameters from Thermogravimetric Data[J]. Nature, 1964, 201: 68-69.

[38] DOYLE C D. Estimating Isothermal Life from Thermogravimetric Data[J]. Journal of Applied Polymer Science, 1962, 6(24): 639-642.

[39] OZAWA T. A New Method of Analyzing Thermogravimetric Data[J]. Bulletin of the Chemical Society of Japan, 1965, 38(11): 1881-1886.

[40] FLYNN J H, WALL L A. A Quick, Direct Method for the Determination of Activation Energy from Thermogravimetric Data[J]. Journal of Polymer Science: Polymer Letters Edition, 1966, 4(5): 323-328.

[41] 赵钧旭, 黄震, 王晓洁, 等. 几种动力学分析方法用于聚乳酸/二氧化钛热分解的比较研究[J]. 数字印刷, 2019(2): 111-121.

ZHAO J X, HUANG Z, WANG X J, et al. A Comparison Study on Analysis of Thermal Decomposition of Polylactic Acid/Titanium Dioxide with Several Kinetic Methods[J]. Digital Printing, 2019(2): 111-121.

Thermal Decomposition Kinetics Analysis of Injection Grade Polylactic Acid

LUO Yuefeng, WEN Huahao, LIAO Zhengfu*

(School of Materials and Energy, Guangdong University of Technology, Guangzhou 510006, China)

The work aims to study the thermal decomposition kinetics of injection grade polylactic acid (PLA) and accurately understand the heat stability of injection grade polylactic acid (PLA), so as to provide theoretical basis for developing high temperature and flame retardant injection grade polylactic acid (PLA) materials. By non isothermal weight analysis, the heating rate of 5, 10, 15, 20 and 25 ℃/min was adopted to analyze the thermal decomposition behavior of injection grade PLA in nitrogen atmosphere. One differential method and three integral methods were used to carry out the detailed kinetics calculation. The correlation coefficient and standard deviation were compared. KAS isothermal integration method was selected, and with relative deviationA=|1–c/e|as the objective function, 16 kinds of thermal decomposition kinetics mechanisms were used to simulate and calculate the most appropriate reaction mechanism for the thermal decomposition of injection grade PLA. The activation energy and pre-exponential factors required for thermal decomposition of injection grade PLA were obtained. The activation energies of injection grade PLA calculated by Kissinger, Madhusudanan-Krishnan-Ninan (MKN), Kissinger-Akahira-Sunose (KAS) and Flynn-Wall-Ozawa (FWO) were 177.01, 174.43, 173.01 and 173.28 kJ/mol, respectively. The pre-exponential factors were 25.84, 26.69-33.75, 25.83-32.89 and 26.38-32.94, respectively. The random nucleation and subsequent growth reaction mechanism (A1/4) are determined and ln(/2)=ln[4.75×109/–ln(1–)]–2.08×104/is the most appropriate description of injection grade PLA thermal decomposition reaction mechanism.

injection grade polylactic acid; thermal decomposition kinetics; non-isothermal analysis; reaction mechanism

TB324

A

1001-3563(2024)07-0045-08

10.19554/j.cnki.1001-3563.2024.07.007

2023-12-13

通信作者