八流方坯中间包控流装置的优化

李 浩 ，李 新 ，陶承岗 ，朱李艳 ，宋瑛洁 ，王欣瑶 ，林小祥 ，吴全俊 ，何 飞

(1.马鞍山钢铁股份有限公司 特钢公司, 安徽 马鞍山 243000；2.安徽工业大学 冶金工程学院, 安徽 马鞍山243032)

中间包是炼钢连铸生产流程的中间环节，是连接钢包和结晶器之间的过渡容器，不仅有储存和分配钢水的作用，而且在提升铸坯质量方面的作用越来越明显[1-3]。中间包的冶金功能很大程度上取决于中间包内流体的流动特性，良好的流动特性可有效提高中间包利用率，降低中间包死区比例，提升铸坯洁净度[4-5]。中间包冶金研究的难点主要在于浇注过程合理流场的稳定性控制，不同中间包內型、不同浇注工艺条件应有不同的控流装置。因此，设计合理的控流装置，优化中间包内型结构，是进行中间包流场控制和达到最佳冶金效果的重要手段[6]。

至今，国内外学者对中间包控流装置优化开展了众多研究。Liu 等[7]、Merder 等[8]、朱正海等[9]研究发现，没有设置控流装置的中间包钢液流动较差，死区体积比例较高，增加挡墙等控流装置后中间包流场得到明显改善。陈远清等[10]通过设计新型控制装置，抑制冲击区液面湍流，使冲击区最大湍动能降低50%，可降低卷渣风险；储成阳等[11]研究发现，加入湍流抑制器后中间包流场得到明显改善，钢液在中间包内停留时间延长，可为夹杂物上浮提供有利条件；王锦等[12]研究发现，中间包冲击区体积对流场的影响最大，导流孔孔径次之、倾角最小。为给不同类型的中间包选择合理的控流装置，Liu等[13]分析高拉速条件下挡墙导流孔对八流方坯中间包钢水流动特性的影响；郑瑞轩等[14]分析挡墙类型、导孔孔径和倾角对四流中间包流场的影响；赵占山等[15]研究发现挡墙导流孔仰角和挡坝高度对六流中间包各流均匀性和夹杂物去除影响较大；王阳等[16]针对无堰坝结构长距离十流中间包，分析湍流抑制器的注流孔内径、数量及开孔方向对中间包流场的影响，发现注流孔内径的影响最显著、数量次之。

综上可知，合理的控流装置(挡墙/堰/坝、湍流抑制器等)，可起到改善中间包钢液混匀效果及各流间不一致性、延长钢液停留时间、降低死区体积等作用，不同控流装置的位置、大小及组合类型对中间包流场特性的影响不同，也是优化中间包控流装置研究的重点。工业生产中，需综合考虑中间包内型结构和浇注工艺条件，选择合理的控流装置组合才能使中间包发挥优异的冶金功能。某钢厂对称结构八流方坯中间包在原控流装置方案下，存在同炉次各流稳定性差、拉速波动大、各流铸坯质量不同等问题，且中间包长宽比大，提高各流一致性和流场优化难度较大。鉴于此，采用物理模拟和数值模拟相结合的方法，在分析原方案中间包流场特性的基础上优化控流装置，最终达到降低中间包死区体积、延长钢液平均停留时间、提高各流一致性和温度均匀性的目标，以期为现场中间包改造和产品质量提升提供依据。

1 模拟实验

1.1 物理模拟实验

1.1.1 物理模型

以某钢厂方坯中间包为研究对象，方坯断面为160 mm×160 mm 和200 mm×200 mm 等，铸机流数为八流，流间距为1 370 mm，公称容量为67.5 t，工作液面为950 mm，溢流液面高度约1 000 mm，大包容量为165 t，浇注周期约56 min，工作拉速约2.6 m/min，铸机弧形半径为12 m。与中间包相匹配的大包长水口内径为90 mm、外径140 mm、浸入深度350 mm，中间包出水口内径为34 mm。

中间包物理模型由有机玻璃制作，控流装置(挡墙和稳流器)、长水口和塞棒等由泡沫板及有机玻璃制作。物理模拟以相似定理为理论基础，遵守几何相似和动力相似。根据相似原理，模型和原型的几何相似比取0.4；根据动力相似[1]，计算出模型和原型的流量比为0.101 2；根据质量守恒定律，由铸坯断面和工作拉速计算出稳态浇注时的原钢包出口流量，然后计算出模型钢包出口流量和中间包各出口流量。实验的中间包原型与模型参数如表1。

表1 中间包原型与模型参数对应关系Tab.1 Correspondence between intermediate package prototype and model parameters

1.1.2 实验过程

第一步为原控流方案中间包实验，挡墙参数如表2，在冲击区设置圆形稳流器用来评估原中间包流场；第二步为中间包控流装置的优化实验，实验方案如表2，主要考虑在圆形稳流器下不同U 型挡墙方案中间包的流场，挡墙和圆形稳流器，如图1。挡墙由2 个对称侧墙和1 个中间墙组成，在每个侧墙设置2 个导流孔，孔径分别为φ1和φ2，位置坐标分别为(x1，y1)和(x2，y2)，仰角分别为α1和α2，偏角分别为β1和β2；在中间墙设置2 个对称的小导流孔，孔径、位置坐标、仰角和偏角分别为φ3，(x3，y3)，α3和β3。从表2 可知，相较原控流方案，优化方案为侧墙2 个导流孔孔径减小且位置提升、中间墙增加带偏角和仰角的小导流孔等。

表2 八流中间包控流装置的优化实验方案Tab.2 Optimization experimental schemes for flow control devices in eight- strand tundish

考虑到八流中间包是对称的，只对左侧的4 个流(1 流、2 流、3 流和4 流)出口进行数据采集，实验装置如图2。实验过程中，采用水模拟钢液，入口冷态水流经长水口、有机玻璃中间包模型、出水口、流量计最终流入排水箱，示踪剂(饱和NaCl 溶液、墨水等)由入口加入中间包，并通过出水口的电极采集电导率信号，经由电导率仪及DJ800 监测系统将电导率信号转化为电压信号，得到各出口的 停 留 时 间 分布(residence time distribution，RTD)曲线及对应的刺激响应时间(滞止时间)、实际平均停留时间、峰值时间等。采用Sahai 等[17]提出的“混合模型”方法计算死区、活塞流和全混流各区体积比例，考虑到多流中间包，采用一致度S定量分析各流流动特性参数的一致性[18]，辅助评价中间包流场。

式中：xmin，xmax分别为各流流动参数xi的最大值和最小值；i为流号。

1.2 数值模拟过程

假设钢水是黏性不可压缩的牛顿流体，忽略中间包表面覆盖剂及渣层对钢液流动和液面波动的影响。中间包内钢液流动可看作三维单相稳态湍流流动，热量传递看作稳态过程，质量传递为非稳态过程。结合中间包钢液实际情况，模型中的流动和传热边界条件设置如下：

1) 固体壁面，采用无滑移边界条件；

2) 近壁区，采用标准壁面函数对速度和湍流特性参数进行修正；

3) 自由表面，忽略渣层的影响，处理为固体壁面，除垂直于表面的速度分量外，其余各变量的梯度为零，垂直于表面的速度分量为零；

4) 对称面法线方向的速度分量为零，且其他各变量的梯度为零；

5) 中间包入口采用速度边界条件，出口采用自由流出边界条件，并且中间包入口和出口处的速度垂直于自由表面，截面上的速度分布是均匀的；

6) 中间包内流体为钢液，物性参数及设置参数如表3；

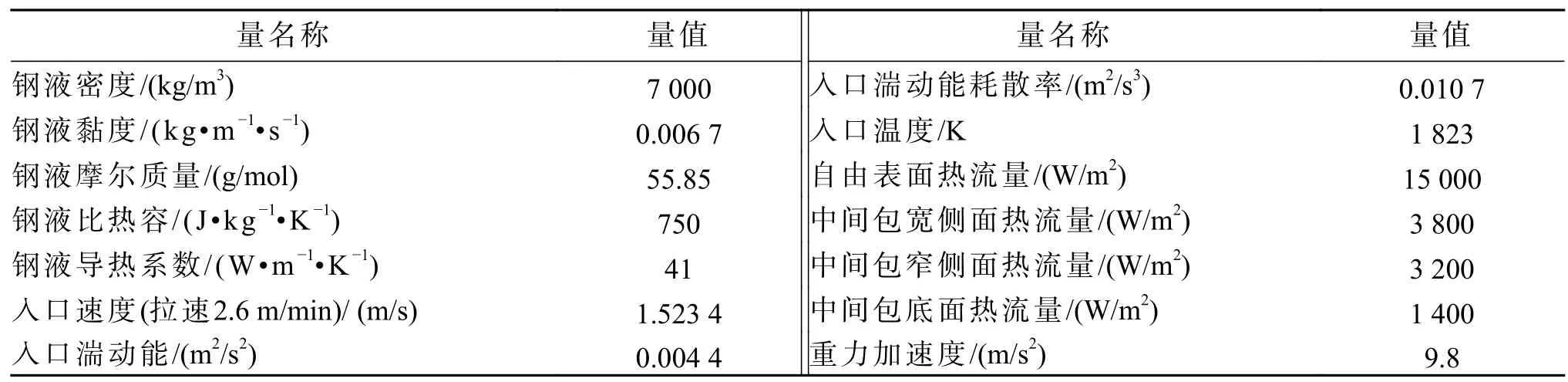
表3 中间包数值模拟设置参数Tab.3 Setting parameters of numerical simulation for the tundish

7) 中间包入口处钢液温度为1 823 K；

8) 中间包包壁和钢液自由表面的散热均视为稳态过程，是第二类边界条件，壁面及表面的热流量为常数[19]。

按照实际全尺寸建立几何模型，考虑到八流中间包是对称的，选择1/2 中间包进行建模。采用正交直角坐标系，利用六面体网格和四面体网格结合的混合网格技术对中间包模型进行网格划分，如图3。在入口、出口及挡墙导流孔区域采用较密的网格划分方式，以保证计算精度，其他区域网格相对稀疏，总网格数在180 万个左右。利用基于有限体积法的CFD/Fluent 软件进行模拟计算，采用Simple 算法求解压力速度耦合方程组。迭代过程中，求解连续性方程、动量方程及湍流方程残差曲线的收敛标准为10-5、能量方程为10-6，离散全部采用二阶迎风格式。得到稳定的流场和温度场后，从钢液入口处以瞬态加入示踪剂0.5 s，然后求解示踪剂在中间包内瞬态的三维湍流传质方程，计算各出口示踪剂浓度随时间的分布曲线。

图3 中间包网格划分Fig.3 Tundish meshing

2 实验结果与讨论

2.1 原中间包流场分布

原控流方案下中间包各出口RTD 曲线如图4，根据图4 计算出的流场特征数值如表4。从表4 可知：对于原中间包流场，死区体积比例达19.04%，减小了中间包有效容积；各流滞止时间、实际平均停留时间和峰值时间一致度分别为26.50%，70.50%和60.31%，各流流动特性一致性较差，尤其是各流响应时间差异较大，第2 流水口在31 s 就出现示踪剂响应，而第4 流水口到117 s 才响应，响应时间差高达86 s，原中间包流场提升空间较大；第4 流也即中间的流与其他流差异较大，主要原因在于原挡墙的开孔方案为侧墙2 个导流孔朝向均是第1 流和第2 流，没有其他导流孔，导致中间包浇注区第4 流和第5 流中间区域存在较大的死区。

图4 原控流方案下中间包各出口的RTD 曲线Fig.4 RTD curve of each outlet in the tundish under the original flow control scheme

表4 原控流方案下中间包各出口RTD 曲线特征数值Tab.4 Characteristic values of RTD curves at each outlet of the tundish under the original flow control scheme

2.2 中间包控流装置的优化

对原中间包控流装置进行优化，通过挡墙导流孔的合理设计(导流孔孔径、仰角和偏角)，延长实际平均停留时间，减小死区体积，并减小各流的滞止时间差、实际平均停留时间差和峰值时间差，提高各流流动特性的一致性。优化控流装置方案1～11 中间包出口RTD 曲线特征数值统计结果如图5，6。

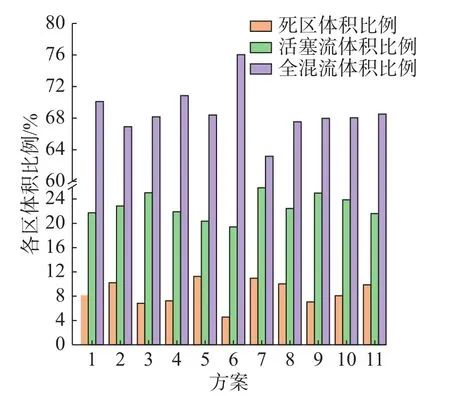
图5 各优化控流方案下中间包各区体积比例Fig.5 Volume proportion of each area in the tundish under various optimized flow control schemes

图6 各优化控流方案流场特征数值及各流一致性曲线Fig.6 Flow field characteristic values and consistency curves of each optimized flow control scheme

由图5，6 可看出：从实际平均停留时间均值选择大于570 s 的方案有方案1、方案3、方案4、方案6、方案9 和方案10，这些方案的死区体积均较小(小于9%)；结合各流流动特性一致性，方案9 的各流滞止时间、实际平均停留时间和峰值时间一致度分别为81.82%，94.43%和80.34%，均超过80%，优于其他方案。

方案9 的RTD 曲线如图7，根据图7 计算出的流场特征数值如表5。由图7 可看出：方案9 各出口RTD 曲线较平缓，不存在尖峰，不易产生短路流，且峰值时间较长，可使钢液在中间包内有很好的混匀效果，利于中间包钢液成分和温度的均匀；方案9 各出口RTD 曲线吻合度较高，较为接近。从表5 可知：相比原方案，最佳方案不仅使中间包死区体积比例由19.04%降至7.06%，活塞流和全混流体积比例也有所增加，且各流水口一致性得到大幅提升，有效改善中间包流场。综合RTD 曲线、各流流动特性一致性和死区体积比例，方案9 为最佳方案。

图7 最佳方案中间包各出口的 RTD 曲线Fig.7 RTD curve of each outlet in the tundish for optimal scheme

表5 最佳方案中间包各出口的RTD 曲线特征数值Tab.5 Characteristic values of RTD curve of each outlet in the tundish for optimal scheme

3 数值模拟结果与讨论

最佳方案(方案9)物理模拟与数值模拟得出的RTD 曲线如图8，图中RTD 曲线的时间和示踪剂浓度均进行无量纲化处理[20]。由图8 可知：数值模拟计算的各出口RTD 曲线与物理模拟实验数据吻合较好，除第4 流出口曲线在峰值部分略有差别，但整体形态基本一致。由此表明数值模拟结果可靠，可用于下一步研究。

图8 最佳方案物理与数值模拟的RTD 曲线Fig.8 RTD curves between physical and numerical simulation for optimal scheme

3.1 中间包流场分布

原方案和最佳方案中间包钢液流线、自由液面速度分布的数值模拟结果如图9～10。

图9 不同控流方案下中间包内钢液的流线Fig.9 Streamline of molten steel in tundish under different flow control schemes

由图9 可知：对于优化前后的中间包，钢液流股从冲击区经过挡墙侧墙导流孔改变流动方向，贴包壁向第1 流和第2 流上扬流动，到达自由液面形成表层流动，然后形成大的循环流分配到各流，但原方案第4 流和第5 流中间区域流线较少，存在死区；相较来说，最佳方案减小了原方案挡墙的侧墙导流孔仰角和孔径，使钢液流股沿表层向远流流得更长，增加了活塞流，有利于非金属夹杂物的上浮和被保护渣的吸收去除，且最佳方案在挡墙中间墙增加2 个带有偏角和仰角的小导流孔，在第4 流和第5 流中间区域流线明显增加，该区域钢液活跃度增强，减小了死区，也增加了第4 流和第5 流的钢液分配量，进一步改善中间包流场。

由图10 可知：原方案和最佳方案的自由液面速度分布差异主要在浇注区，对应最大流速分别为0.151 2，0.114 4 m/s，优化方案从挡墙导流孔出来的钢液流股向上对自由液面的冲击大大减小，减少了液面波动和卷渣风险。

图10 不同控流方案下中间包自由液面的速度分布Fig.10 Velocity distribution of free liquid surface in tundish under different flow control schemes

3.2 中间包温度场分布

图11 为原方案和最佳方案的中间包内钢液温度场分布。由图11(a)可知：对于原方案，中间包内钢液最高和最低温度分别为1 823.000，1 804.814 K，相差18.186 K，原方案中间包温度场不均匀性较大；原方案各出口钢液温度分别为1 816.922，1 818.149，1 818.482，1 817.502 K，最大相差1.560 K。由图11(b)可知：对于最佳方案，中间包内钢液最高和最低温度分别为1 823.000，1 806.996 K，相差16.004 K，比原方案中间包最大温差下降2.182 K；最佳方案各出口钢 液 温 度 分 别为1 817.627，1 817.245，1 817.848，1 817.861 K，相差0.616 K，比原方案各出口温差下降了0.944 K。由此可知，优化控流装置后，中间包内钢液温度场分布比较均匀，而且明显改善原方案在第4 流和第5 流中间位置上部的低温区。

图11 不同控流方案下中间包内钢液的温度场Fig.11 Temperature field of molten steel in tundish under different flow control schemes

4 结论

为改善中间包冶金效果，以某钢厂八流方坯中间包为研究对象，采用物理模拟与数值模拟相结合的方法分析挡墙导流孔数量、孔径、位置和倾角对中间包钢水流动特性的影响，优化中间包控流装置，得到以下主要结论：

1) 对于原方案中间包流场，死区体积比例达19.04%，各流滞止时间、实际平均停留时间和峰值时间一致度分别为26.50%，70.50%和60.31%，各流一致性较差，尤其是第4 流与其他流差异更大。主要原因在于原挡墙的开孔方案是侧墙的2 个导流孔朝向均是第1 流和第2 流，没有其他导流孔，导致中间包浇注区第4 流和第5 流中间区域存在较大的死区。

2) 通过改变挡墙侧墙导流孔孔径、仰角和偏角及在中间墙增加导流孔优化中间包控流装置，优化的中间包各流RTD 曲线较平缓，不存在尖峰，不易产生短路流，且峰值时间较长，死区体积比例由原中间包的19.04%降至7.06%，活塞流和全混流体积比例也有所增加，且各流滞止时间、实际平均停留时间和峰值时间一致度分别为81.82%，94.43%，80.34%，均超过80%，各流一致性大幅提升，有效改善中间包流场特性。

3) 减小原挡墙的侧墙导流孔仰角和孔径，钢液流股沿表层向远流得更长，增加活塞流，且对自由液面冲击大大减小，同时在挡墙中间墙增加带偏角和仰角的小导流孔，可进一步改善中间包第4 流和第5 流中部流场。对于最佳方案，中间包最大温差为16.004 K，比原方案下降2.182 K；各出口钢液最大温差为0.616 K，比原方案下降0.944 K，中间包内钢液温度场分布更均匀，且明显改善第4 流和第5 流中间位置上部的低温区。