求解高维函数的果蝇免疫协同优化算法∗

张晓茹 王 丹 周锦程

（1.黔南民族医学高等专科学校 都匀 558000）（2.黔南民族师范学院数学与统计学院 都匀 558000）（3.黔南民族师范学院复杂系统与智能优化实验室 都匀 558000）（4.黔南民族师范学院计算机与信息学院 都匀 558000）

1 引言

伴随经济的高速发展，优化问题不断涌现，群体智能算法随之而生并获得广泛应用［1～3］。2011年，Pan 教授［4］从果蝇嗅觉、视觉特征出发，提出果蝇优化算法（fruit fly optimization algorithm，FOA），因其诸多优点［5］而成为各领域的研究焦点。该算法在收敛效率等方面却不甚理想，致使改进型的果蝇算法［6～9］涌现，旨在增强算法前期全局与后期局部的搜索能力，以提高算法的优化效果和效率。但是，大多改进工作主要是对基本FOA 算法缺陷的修补。而昆虫学表明［10～15］，果蝇仅凭借先天性的三重免疫防线即可高效抵御病原物质的入侵，此为算法设计的灵感来源。而着眼于果蝇自身简单又高效的免疫机制，探究关于果蝇免疫算法的工作较为稀缺［16］。故本文从果蝇先天免疫系统应答模式出发，继续探讨求解高维函数的果蝇免疫协同优化算法（Cooperative Fruit-fly immune optimization algorithm，CFIOA）。

本文的创新点在于充分模拟果蝇先天防御机制的黑化作用、细胞免疫及体液免疫之间的协同应答模式，提出果蝇先天性免疫理论模型及果蝇免疫协同优化算法。

2 免疫理论及算法描述

2.1 果蝇先天性免疫理论模型

果蝇仅有先天性免疫机制，缺少T 细胞、B 细胞、抗体及补体，而作为传播细菌等的载体，却能保障自身安全，主要依靠其三种协同应答的先天性免疫机制［10～15］。黑化作用作为第一道防线，是抵御病原微生物最直接的免疫反应。当果蝇表皮受损时，将诱导蛋白酶水解，产生凝血及黑化作用，进一步促进伤口的愈合，抑制微生物的繁殖［10］。细胞免疫主要包括吞噬、黑化和包裹作用，以达到清除病原的目的，其中吞噬是最主要的免疫方式［12］。Toll 信号通路和Imd 信号通路构成主要的体液免疫，不同果蝇机体被传染，将激活相应的Toll或Imd，产生与之对应的抗菌肽，分泌到血淋巴中，以清除入侵病原体等［10］。

实际上，果蝇的三种先天性应答机制不是独立工作，却是相互影响、协同作用的。体现在：1）体液免疫对血细胞的功能有一定程度的影响，另外黑化作用中又需要晶细胞；2）Toll 信号通路一定程度上促进体液免疫、细胞免疫的相互作用［11］，并且它的激活又是这两种应答协同免疫的结果；3）黑化作用一方面可以促进伤口的愈合，另一方面又与吞噬作用、包裹作用相关联［13］。综上，获得果蝇先天性免疫理论模型，如图1。

图1 果蝇先天性免疫理论模型

2.2 算法描述

求解如下问题（P）：

其中，D为有界的闭区域，维数n≤1000；f(x)为优化的目标函数，候选解x∊D，x=(x1,x2,…,xn)。由函数最值定理知，问题（P）必有最优解。

模拟上述果蝇理论模型，获得CFIOA的算法流程图，见图2。此算法由内、外两个循环构成，其中内循环主要模拟清除入侵微生物的免疫过程，对同一种群中的个体同步执行进化、个体数量递减的操作，以高效寻求各子群的优质个体；外循环负责动态更新所获的最优个体，以高效获取群体最优。为方便算法描述，将果蝇个体视为问题候选解，外来有机体对应于求解问题（P）的最优解。结合图1 和图2，具体算法如下。

图2 CFIOA流程图

步骤1 参数设置：种群总规模记N，最大外循环、内循环的迭代数依次记Gout、Gin，选择率参数ω，α,β,δ；

步骤2 置外循环数t←1。生成N个随机个体，即初始种群P(1)，计算个体距离并归一化。记第t代种群为P(t)，其最优个体记xbest；

步骤3 模拟黑化作用：依据阈值α除去P中较弱个体，剩余个体则成种群P*；

步骤4 置内循环数m←1。种群划分：随机选取P*中w(1-α)N个体组成A 群；依阈值β将P*-A划分为稀疏群体B、稠密群体C；

步骤5 模拟免疫过程：

步骤5.1 群体A、B、C的最优个体分别记Abest、Bbest、Cbest，进一步更新群体最优xbest；各子群按照适应度的优劣各删除δ%劣质个体；

步骤5.2 模拟细胞免疫：群体A 的个体xj的进化策略：

获种群A*。a、b是搜索区间左、右端的向量；s=min{x-a,b-x}，xdist是x到A的距离；

步骤5.3 模拟Toll 信号通路：种群B 中个体xj的更新策略：

获种群B*。r是0～1之间的随机数；

步骤5.4 模拟Imd 信号通路：种群C 中个体xj的变异策略：

获种群C*。其中：

步骤5.5P(t)←A*∪B*∪C*。若P（t）中最优个体优于xbest，则及时更新xbest；

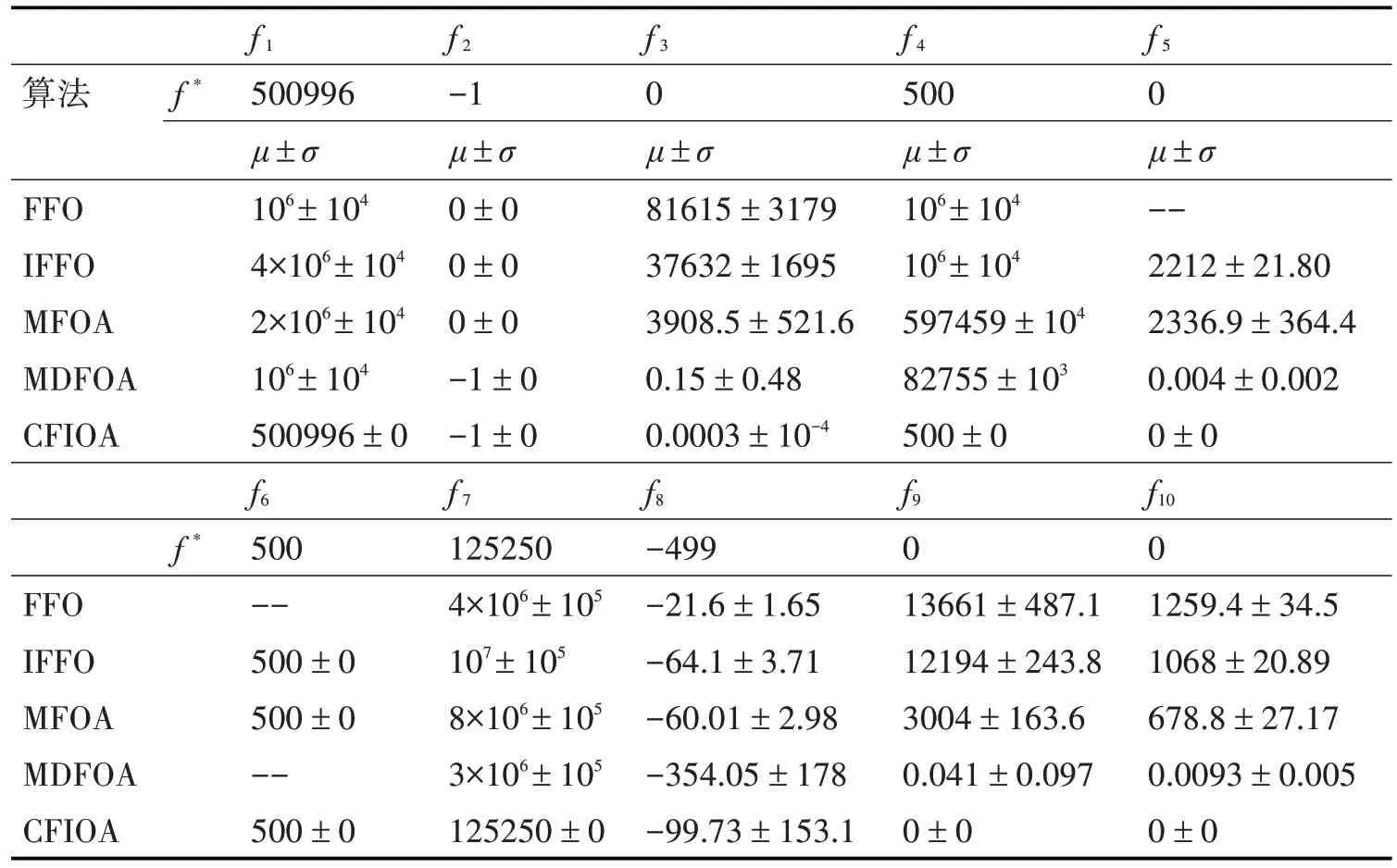
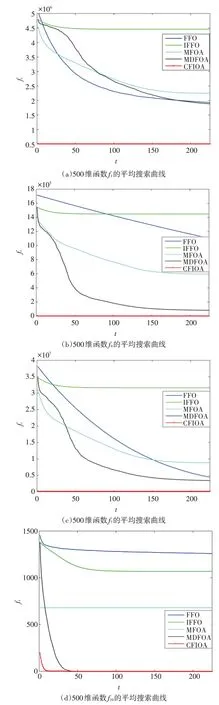
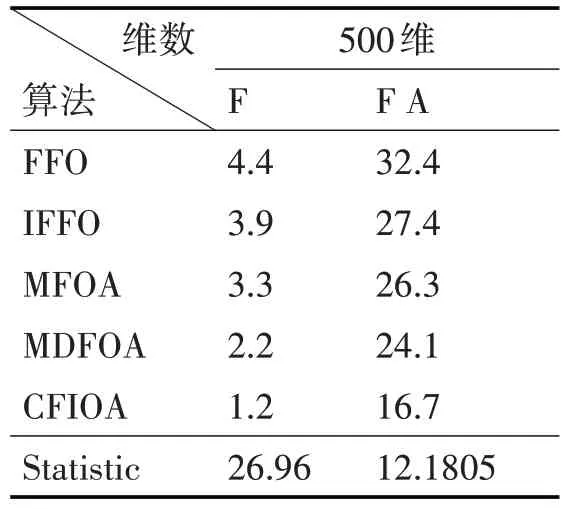
步骤5.6 若m

步骤6 若t

否则，输出xbest。

在上述算法设计中，步骤3 对应黑化作用的免疫过程；步骤5.2 模拟细胞免疫中吞噬、包裹机制，并结合最优个体Bbest、Cbest来确定新个体的进化方向；步骤5.3、5.4 借助最优个体Abest、Bbest、Cbest及xbest的相关信息，实现个体更新，受启发于三种免疫机理的协同应答机制。

3 数值实验

借助Windows 10/CPU 3.60GHz/RAM 16.0GB/VC++平台进行数值统计实验与分析。比较算法有近年公开发表的FFO［17］、IFFO［17］、MFOA［18］和MDFOA［19］。测 试 函 数 有 单 模 态（f1～f7）和 多 模 态（f8～f10），测试区域与文献［5］一致。测试函数的搜索区域既有非对称区间又有对称区间，搜索区域范围相差较大，能充分检测算法的全局搜索与局部挖掘能力。各算法在相同参数条件N=60，G=225下独立求解每个问题100 次，其他参数与相应文献设置相同。通过多次数值实验的比较与分析，CFIOA中的参数分别取值为

为测试各算法求解高维函数的优化能力，以上算法在维数n=500 时展开数值实验比较与分析（文献［5］已对n=100、200 维的数值比较实验与算法性能进行分析），以比较各算法求解类型多样的高维函数优化的共性和个性；另外，为验证本文算法CFIOA 具有更强的优化能力，特进行维度n=800、900及1000的求解实验。

3.1 500维数值实验与性能分析

取定n=500，上述算法独立进行求解各问题100次，各算法优化的均值如表1；绘制函数f1、f4、f7、f10的平均搜索曲线如图3。其中，f*为500 维时各函数的理论最优值；t为算法迭代次数；ft为100 次独立运行下第t代群体搜索到的最优值的均值。

表1 500维的统计结果

图3 500维函数f1、f4、f7、f10的平均搜索曲线

从表1 的数值对比发现，高维函数优化对算法模块的设计、算法搜索能力、求解效率等方面均提出了较大挑战。随着问题维数的增加，除CFIOA外，四种参与比较的算法呈现倍数甚至指数级的下降。而CFIOA 在10 个求解问题中，仍有80%的函数可以达到理论极值，说明该算法受问题维数的影响较小。结合文献［5］，CFIOA 对于f8的优化结果看，随着问题维数100、200、500 的增加，所获得的的优化均值分别为其理论极值的47%、35%、20%，持续下降的优化极值占比，说明高维多模态函数的优化难度较大，对算法模块的设计有更高的要求，但CFIOA求解该问题的均方差较大，说明该算法的种群多样性得以维持，各子群协同进化的模块设计保证了算法的优化效果与算法的收敛性。结合表1 与图3 信息可知，CFIOA 较其他比较算法而言，其寻优速度、收敛精度（除f8外），种群多样性等方面均有较为明显的优势，受问题维数的影响也相对较小，进一步验证了该算法CFIOA的优化稳定性和寻优效率。

3.2 算法差异性分析

为明确算法的优化效率，获得500 维时，各算法单独求解10个问题100次的时间均值，如表2。

表2 各算法的平均运行时间分析（单位：s）

对比表2 各算法优化不同维度函数的平均运行时间可知，对于同一维度的函数，CFIOA 所需时间最短，源于其内、外循环的模块设计以及模拟黑化作用的淘汰方式在很大程度上降低了计算量，进而缩短了运行时间，其他算法依次是IFFO、MDFOA、FFO、MFOA。

为分析各算法所获得的优化解是否存在明显差异，以上述算法求解各问题的平均优化值为样本，依托Friedman［20］和Friedman 秩检验［20］方法，将结果统计在表3。特别地，显著性水平取α=5%且有

表3 各算法秩检验结果

从表3数据知，优化问题为500维时，本文算法一方面具有最小的F 值以及FA 值，另一方面获得的统计值都大于5.99。综上说明，CFIOA 获得了优于其他比较算法的解，其解的质量存在显著性优势［20～21］。

3.3 CFIOA的高维性能测试与分析

算法CFIOA 独立求解维数为800、900 及1000时的f1～f10各100次，获得的优化目标均值如表4。

表4 CFIOA关于800～1000维函数的优化结果

由表4 的数据信息知，算法CFIOA 求解维数为800、900、1000 时分别有60%、40%、30%的函数可以搜索到理论极值，说明问题维数的增加对算法寻优性能提出了更高、更全面的挑战。对于问题f1、f4、f7、f8时，随维数的增加，难以搜索到理论极值，却具有较大的均方差，从而有相差较大的最优解，一方面说明该算法的个体信息具有多样性，另一方面也说明该算法的局部与全局搜索能力较好，有能力跳出局部极值，更进一步保证了算法的持续寻优。但该算法CFIOA 仍存在不足，如参数灵敏度的调控、高维函数的优化精度等，如何平衡好算法优化效果与求解效率将是下一步完善算法设计的关键。

4 结语

果蝇极为简单有效的先天性免疫机制，使得作为细菌、真菌传播载体的果蝇自身而不被感染，受此启发着眼于果蝇先天性协同免疫机制，构建果蝇免疫理论模型，进一步获得果蝇免疫协同优化算法。各种免疫机制独立又相互影响的应答机理是协同思想设计的主要来源，这为算法的模块设计提供了思路。大量数值结果及分析可知，算法CFIOA在搜索速度、前期全局、后期局部、种群多样性、跳出局部极值等方面的能力具有明显优势。