数字式配流摆线液压马达特性研究

陈宝，刘万星，陈刚，付江华，马维忍

(1.重庆理工大学车辆工程学院，重庆 400054；2.重庆工商职业学院智能制造与汽车学院，重庆 401520；3.金康新能源动力有限公司，重庆 400000)

0 前言

摆线液压马达具有结构紧凑、超载保护容易等特点，广泛应用于搅拌车、压路机和农业机械等低速重载传动场合。目前，市场上应用的摆线液压马达配流方式多为轴配流或盘配流等机械配流方式。由于存在设计与加工误差，配流机构无法精确与工作腔相匹配，造成困油现象，马达机械效率和容积效率下降。另外，机械配流只能实现马达单速运转，在需要调速的场合，常常同变量泵或变量阀组成调速机构，大大限制了摆线马达的使用场景[1-2]。

为此，众多生产厂家与学者不断革新摆线马达配流机构，其研发成果多为专利。孔祥臻、纪方[3]在端面配流阀体内加工有容积不等的密封槽容腔，通过双速阀芯控制进入油室油量，实现马达高低速切换。孙燕等人[4]提供一种新的马达配流控制方法，通过配流阀控制若干配流通道的通断，以控制进入若干环腔及啮合腔的流量，可以实现马达多转速调节。张智敏等[5]在配流联动轴和花键轴之间增加挡块，挡块两端与转子内花键相连，减少马达花键轴的长度，使摆线副受力均匀。花逸峰等[6]在原有轴配流摆线马达的基础上，增加一对隔盘和一个O形圈，打破了以往马达配流轴和输出轴为一体的传统结构，提升马达径向承载能力。王志生等[7]用母线倾斜的腰型孔代替传统径向孔，使配流孔与配流槽的相对运动具有过渡性，改善了马达配流特性。泮健[8]用高速电磁开关阀代替机械配流机构，运用到径向柱塞式液压马达研究中，试验结果表明：该液压马达的主要输出特性均优于机械配流马达。

本文作者所提出的数字式配流摆线液压马达是通过高速电磁阀组取代传统的机械配流机构而形成的一种新型摆线液压马达。运用计算机控制技术，将配流方式由机械位置式转变为时间控制式，从而有望从根本上克服机械配流的固有缺点。不仅可以降低马达配流机构的加工难度，且大大提升了配流与调速控制的灵活性。

1 数字式配流摆线马达工作原理

数字式配流摆线液压马达的配流结构方案如图1所示。7个三位四通电磁阀P、T油口分别连接液压站的高压油泵和回油箱，A口通过高压油管连接马达7个相应啮合腔，实现进、回油，B口始终封闭。马达本体如图2所示。

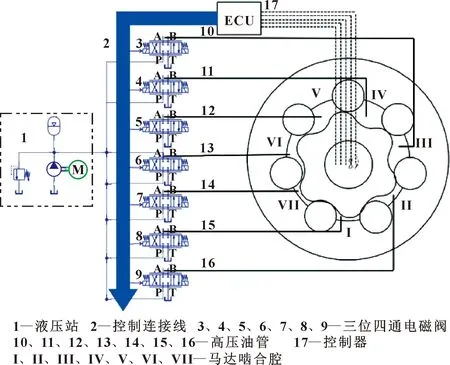
图1 数字式配流摆线液压马达结构方案

图2 数字式配流摆线液压马达本体结构

由图1可知，通过控制高速电磁阀左右两端电磁铁的通电时序实现啮合腔内的进、泄油。在摆线马达运行过程中，电磁阀右端电磁铁通电时，A口与P口导通，实现进油；左端通电时，A口与T口导通，实现回油。马达啮合腔根据工作状态，处于高压区间的工作腔进油，其电磁阀右端电磁铁得电，高压油经相应电磁阀A口，通过高压油管流入对应的高压腔内，其回油口关闭；同时，处于低压区间的工作腔回油，其电磁阀左端电磁铁得电，低压油经相应电磁阀 A口，通过高压油管流入油箱，其进油口阀关闭。在电磁阀两端都断电后，阀芯处于中位，此时马达工作腔内的油液因与油箱油路中断而能够立即停止，保证了液液压设备使用的紧急安全性能。

根据摆线马达的配流过程，可以得出摆线马达输出轴转角与高、低压油腔及对应高速电磁阀的通电时序，即数字配流摆线马达配流状态，如表1所示。表中Ⅰ～Ⅶ分别为摆线马达工作腔及对应的高速电磁阀。

表1 逆时针配流状态

2 数学模型

2.1 高速电磁阀流量模型

高速电磁阀的动态特性直接影响整个液压动力系统的正常运行。因此，建立可靠的电磁阀动力学模型对于系统仿真及其控制具有重要意义。该模型必需处理阀的3个子系统[9-10]。

(1)电磁子系统模型

根据基尔霍夫电压定律：

(1)

式中：U为励磁电压；i为线圈励磁电流；Rc为磁路电阻；Lc为电磁线圈电感。

根据工程应用中的经验公式，直流螺线管的电磁力：

(2)

式中：N为线圈匝数；μ0为真空磁导率；kf为漏磁系数；δ为气隙长度，δ=x0-x(t)；S为磁路截面积。

(2)机械子系统模型

当电磁阀通电时，电磁铁吸合衔铁，并通过推杆使阀芯产生位移。因此，机械子系统主要包括衔铁和阀芯两部分。对于衔铁受力分析，根据牛顿第二定律：

(3)

式中：k为弹簧刚度；δ为弹簧预紧量；B为黏滞阻尼系数；Fw为负载作用力；m为衔铁质量。

阀芯位移方程：

(4)

式中：xf(t)为阀芯位移；Fi为液动力；Fi=Fs+Fw；mf为阀芯质量。

阀芯稳态液动力方程：

Fw=2cqcvω(pr-pf)xf0cosθ=kwxf0

(5)

式中：cq为阀口流量系数；cv为流体通过阀口的速度系数；ω为阀口面积梯度；pr、pf分别为流体流入、流出阀口时的压力；θ为射流角；xf0为阀芯开度；kw为液动力刚度系数。

阀芯瞬态液动力方程：

(6)

式中：L0为阀腔长度；ki为阻尼系数。

(3)流量模型

阀口流量方程：

(7)

式中：A为阀口过流截面积；Δp为阀口压差；ρ为油液密度。

2.2 摆线液压马达动态转速模型

以马达顺时针转动为例，建立摆线马达静态及动态转速模型。

摆线马达的7个密闭容腔的容积变化周期为π/3，相邻两容腔容积变化相位差为π/21，如图3所示。因此，只需计算Ⅰ号腔容积V1，然后根据相位差可得到各啮合腔的容积变化，进一步得到马达高压腔的容积变化。

图3 摆线啮合副示意

图中，M1、M2为摆线与两针齿的啮合点，N1、N2为两针齿间的啮合临界点。则Ⅰ号容腔容积：

V1(θ)=B(SO1M1N1+SO1M2N2+SO1N1N2-SO1M1M2)

(8)

其中：

(9)

式中：tb，1|M1、tb，7|M2为定子啮合点位置参数；tb，1|N1、tb，7|N2为Ⅰ号腔摆线啮合临界点位置参数；t1、t2为转子曲线参数。

根据数字摆线液压马达配流机制，电磁阀输出的高压油液进入马达工作腔，根据流量连续性方程可得：

(10)

根据能量守恒定律，可得到摆线液压马达的输出扭矩：

(11)

转矩平衡方程：

(12)

式中：TL为负载转矩；J为负载转动惯量。

同理，可得到逆时针转动时马达的动力学方程。

3 模型仿真

在建立数字式摆线马达数学模型后，进行相应的模拟来初步研究该摆线液压马达的特性。表2为数字摆线马达相关仿真参数。电磁阀相关结构参数参考DSG-02-3C2-DL型电磁阀。

不考虑马达工作腔内的摩擦阻力矩，对阀-马达一体结构搭建Simulink仿真模型，如图4所示。

图4 阀-马达一体仿真模型

在PWM频率100 Hz、100%占空比时，马达的双向配流转速输出曲线如图5所示。以顺时针输出转速曲线为例，马达输出转速在0.1 s内由0增大到最大值199.3 r/min，之后转速一直在[177.8，199.3]r/min区间内不断波动，这是由马达进油腔总容积不断变化造成的。另外，无论是马达顺时针旋转还是逆时针旋转，马达高压腔总容积的变化是相同的，因此，顺时针和逆时针方向的转速输出曲线完全对称。

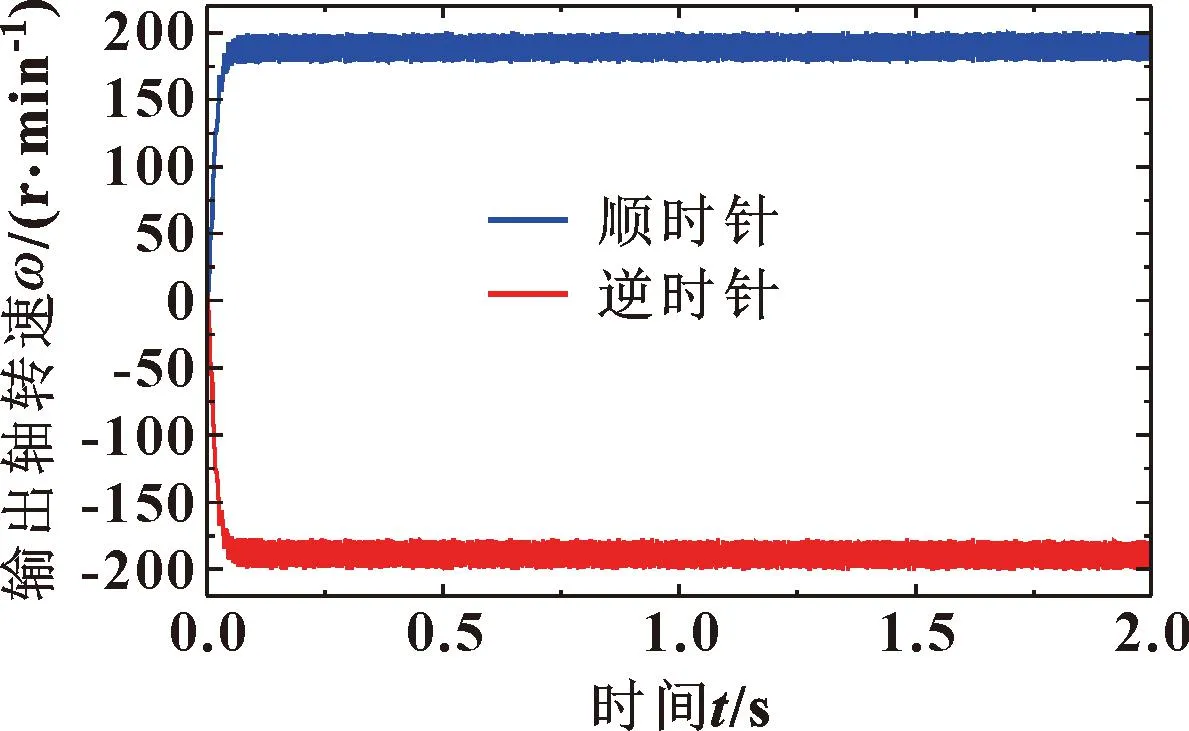
图5 双向配流输出转速曲线

由于摆线马达在实际运转过程中，常会出现在某一时刻切换转向的工况。数字式配流摆线马达可通过在某时刻改变电磁阀通电时序，实现马达转向的双向切换。其顺-逆、逆-顺的转向切换仿真曲线分别如图6、7所示。仿真结果表明数字式配流摆线马达能够顺利实现转向的双向切换。

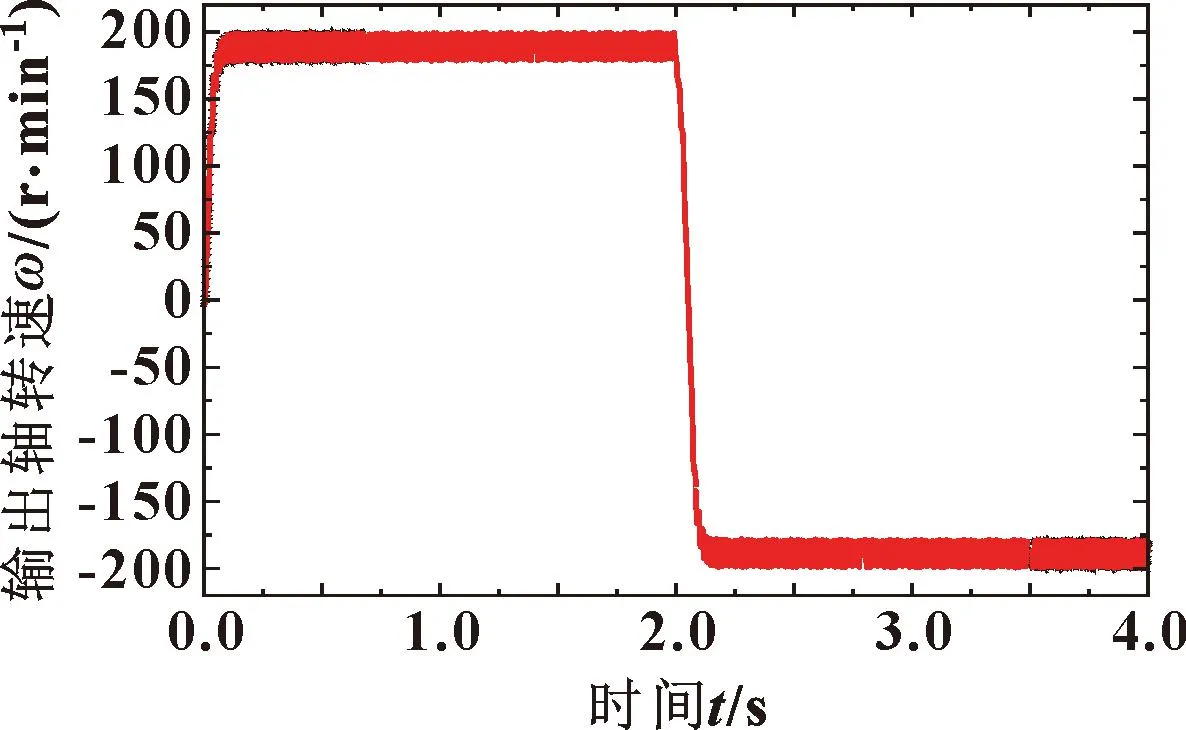
图6 顺-逆时针配流仿真曲线

图7 逆-顺时针配流仿真曲线

在PWM占空比分别为100%、80%、60%下的转速输出曲线如图8所示。可知：在占空比为100%时，马达转速曲线在[177.8，199.3]r/min之间波动；占空比为80%时，马达转速曲线在[144，152.6]r/min之间波动；占空比为60%时，马达转速曲线在[99.1，106.5]r/min之间波动。不同占空比下的平均转速如表3所示。可知：通过改变占空比，可确定所需要的转速。

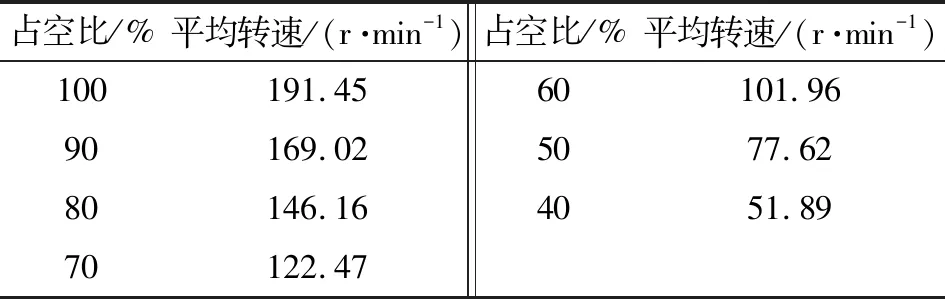
表3 不同占空比下的仿真调速特性

图8 不同占空比转速仿真曲线

4 结论

本文作者介绍了数字式配流摆线液压马达的结构方案。在分析数字式配流机制的基础上，分别对电磁阀和摆线马达建立数学模型。阀-马达模型的仿真结果表明：数字式配流方案能够使电磁阀组和马达按照配流时序正常工作。并且，通过输入不同占空比，马达的输出转速不同，占空比越大，马达平均转速越高，转速波动范围越大。因此，数字式配流摆线马达能够在实现数字配流的同时，还能实现调速功能，这将为液压伺服调速控制系统提供不同的研究方向。