航空发动机燃油雾化喷嘴流量预测方法的研究

彭枢廷，陈福振，严红

(西北工业大学动力与能源学院，陕西西安 710072)

0 前言

燃烧室是航空发动机三大部件之一，其性能直接影响整个发动机的工作性能。为了满足新一代军用战机对更高推重比、更高机动性、更高可靠性和耐久性的需求以及民用客机对低污染、低油耗的需求，现代航空发动机对燃烧室性能提出了更高的要求。其中燃油雾化作为燃烧室燃烧工作的初始阶段，对燃烧室的性能有着至关重要的影响，因此需要重点关注燃油雾化喷嘴。燃油雾化喷嘴尺寸小，内部流动复杂，微小的尺寸和表面光度的变化都会对雾化效果带来影响，研究其内部流动特性以及流量变化规律对喷嘴的设计校核有重要作用。

到目前为止，通过数值模拟技术，研究者们对喷嘴流动特性展开了大量研究[1-10]，计算了喷注参数、物性参数、喷嘴结构参数以及方位参数对流量系数的影响，分析了喷嘴流动特性，一定程度上掌握了工质在喷嘴内部的流动规律。另外通过计算喷嘴流量并与参考流量进行比较，对喷嘴进行了校核与改进工作[11-12]。在实验方面，研究者们通过搭建实验台，进行了大量实验，分析了喷注参数以及关键几何参数对喷嘴流量的影响，得到了喷嘴流量的变化规律[13-15]。

到目前为止，现有的数值模拟研究大多只计算喷嘴的局部几何模型，对喷嘴上游管路的关注较少，难以准确指导喷嘴喷注参数的选取。另外，现有的研究大多只关注了喷嘴的流量系数以及喷嘴内工质流动的现象，仅对目标喷嘴流量变化曲线进行测试并拟合得到流量预测的经验公式，未形成喷嘴流量随相关参数变化的理论预测模型，拓展性较弱。因此，探究喷嘴内部规律并建立一种具有良好拓展性的喷嘴流量理论预测模型具有重要意义。本文作者基于此想法，对某型号航空发动机燃油雾化喷嘴进行了建模计算，对燃油从主副油路供油管到喷口间的流动过程进行分析，得到影响喷嘴流动的关键部位。最后，选取了关键几何参数，根据得到的计算结果，推导了喷嘴流量的理论预测模型并与实验结果进行了对比。

1 数值模拟方法

1.1 几何模型构建与网格划分

为了关注燃油在喷嘴内部完整的流动过程及其流动特性，对主油路、副油路进行了分别建模计算，建立的整体喷嘴几何模型及局部网格示意如图1所示。

图1 喷嘴几何模型(a)及局部网格(b)示意

为了获得关键部件(主油路底杯、涡流器、副油路喷口前部)的尺寸与燃油流量之间的关系，进行几何模型构建与网格划分。数值计算所涉及的关键几何参数如表1所示。关键部位几何模型与网格示意见图2。

表1 关键几何参数 单位：mm

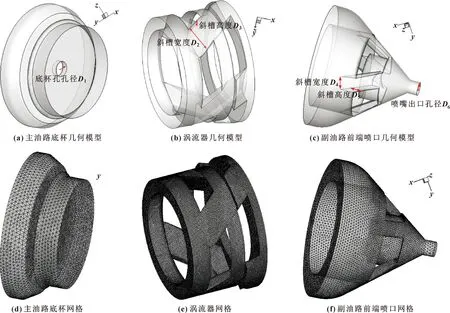
图2 关键部位几何模型与网格示意

1.2 数值模拟与结果分析

1.2.1 控制方程与湍流模型

燃油在喷嘴内的流动属于一种典型的牛顿黏性流动过程，以不可压缩Navier-Stokes方程进行描述：

(1)

式中：ρ为流体密度；u为流体流动速度；ν为运动黏度。

为了准确描述喷嘴内部强旋流的复杂流动，采用RNGκ-ε湍流模型描述湍流，方程如下：

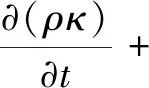
(2)

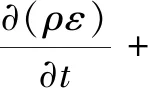
C2ερε2/κ-R

(3)

1.2.2 离散格式

由于中心差分格式的不稳定性和一阶迎风格式的不稳定性和低精度，同时考虑物理量受节点间分布曲线曲率的影响，对对流项采用高阶迎风格式的二阶迎风格式，扩散项采用中心差分格式，对时间项的离散格式采用全隐式方案。

1.2.3 仿真结果与分析

图3为计算获得的副油路管道内流体流动与压降的情况，可以看到：流体由于流过的距离较远，有明显的沿程损失，发生了压降。

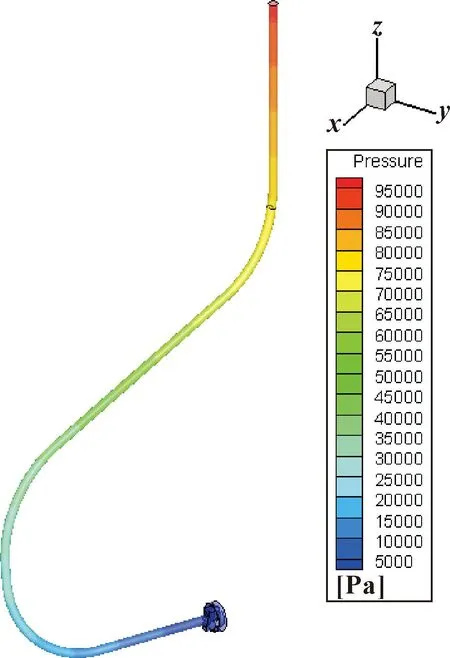
图3 副油路管道内流体流动与压降

图4为副油路活门内芯内流体压降与流线分布情况，可以看到：在活门开启的截面处，由于截面面积变化，发生了明显的压降。图5为副油路喷嘴前部流体压降与速度矢量分布，可以看到：流体在进入4个斜槽后压降较为明显，同时流体通过锥形结构之后到达最小出口时，再一次发生大的压降，这时速度增加较为明显，同时可以看到明显的旋流现象产生。表2列出了计算获得的副油路管路和活门芯内压降数据。

表2 副油路活门内芯和油管内结构尺寸及液体压降

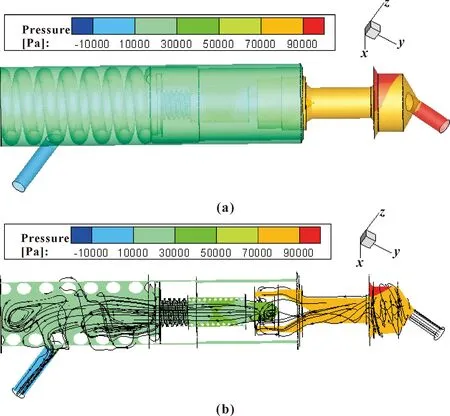
图4 副油路活门内芯内流体压降(a)与流线分布(b)

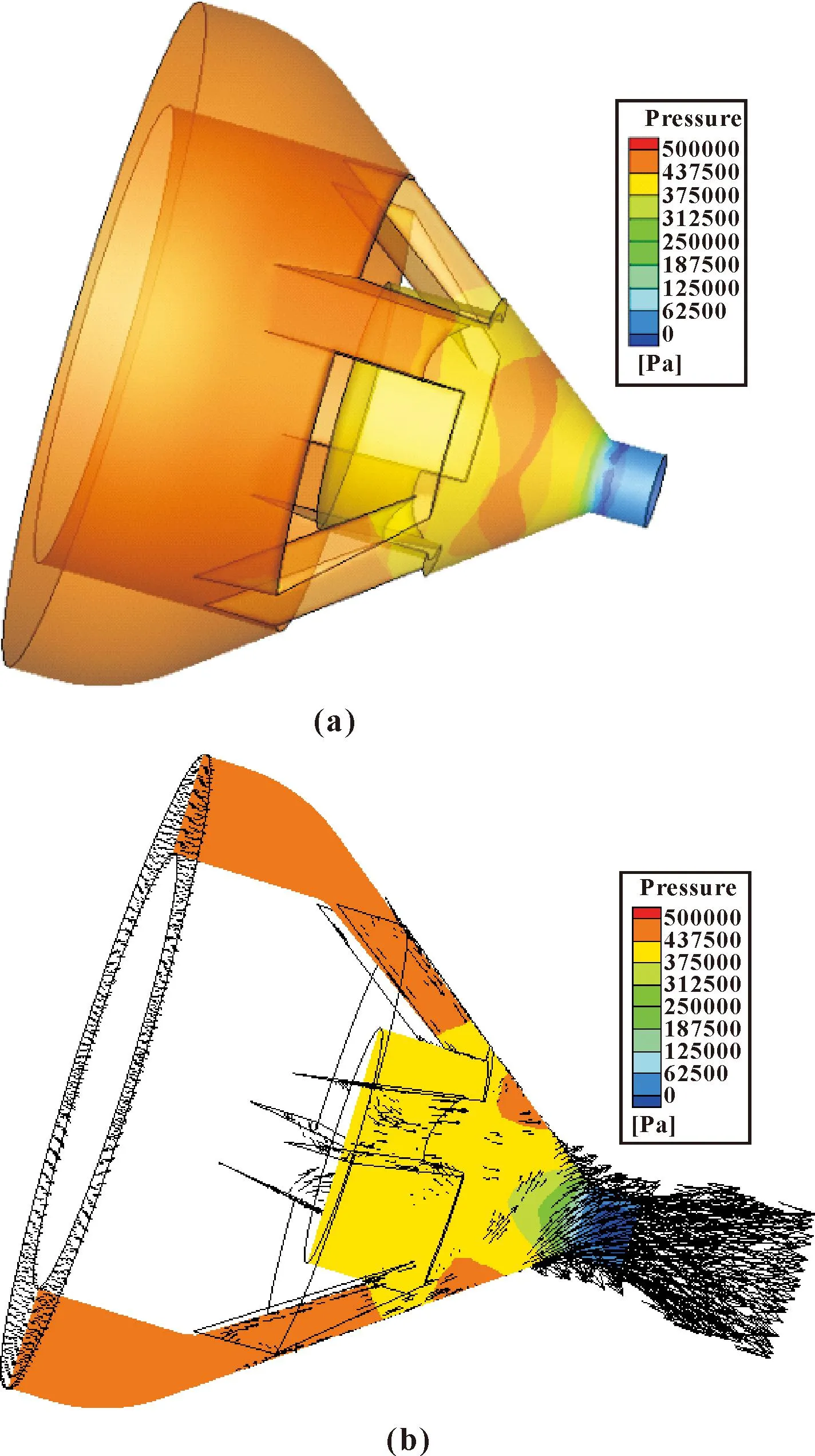
图5 副油路喷嘴前部流体压降(a)与速度矢量分布(b)

图6为计算获得的主油路底杯内流体流动与压降情况，可以看到：底杯中心孔径是影响流体压降最核心的因素。图7为主油路喷口出口附近涡流器结构内的流体流动与压降，可以看到：压降产生较为明显的地方是进入旋流槽部位处，而在出口处基本再无压降产生。图8为主油路活门内芯内流体压降分布情况，可以看到：由于主油路的活门内芯控制的开口截面是在活门下游，因此压降也发生在下游截面处。图9为主油路油管内流体流动与压降情况，可以看到：由于流体在管道内流动没有经过阀门或凹凸台等部件结构，因此压降较为均匀，沿程损失较为均匀，主要由管壁摩擦等因素造成。表3为计算获得的主油路活门内芯和油管内结构尺寸及液体压降数据。

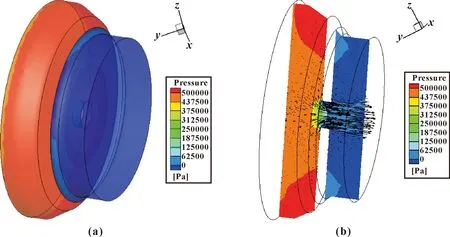
图6 主油路底杯内压降(a)与流体流动速度矢量分布(b)

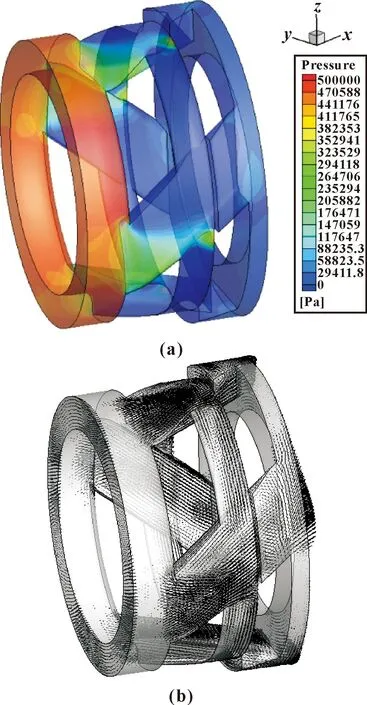
图7 涡流器内压降(a)与流体速度矢量分布(b)

图8 主油路活门内芯内流体压降

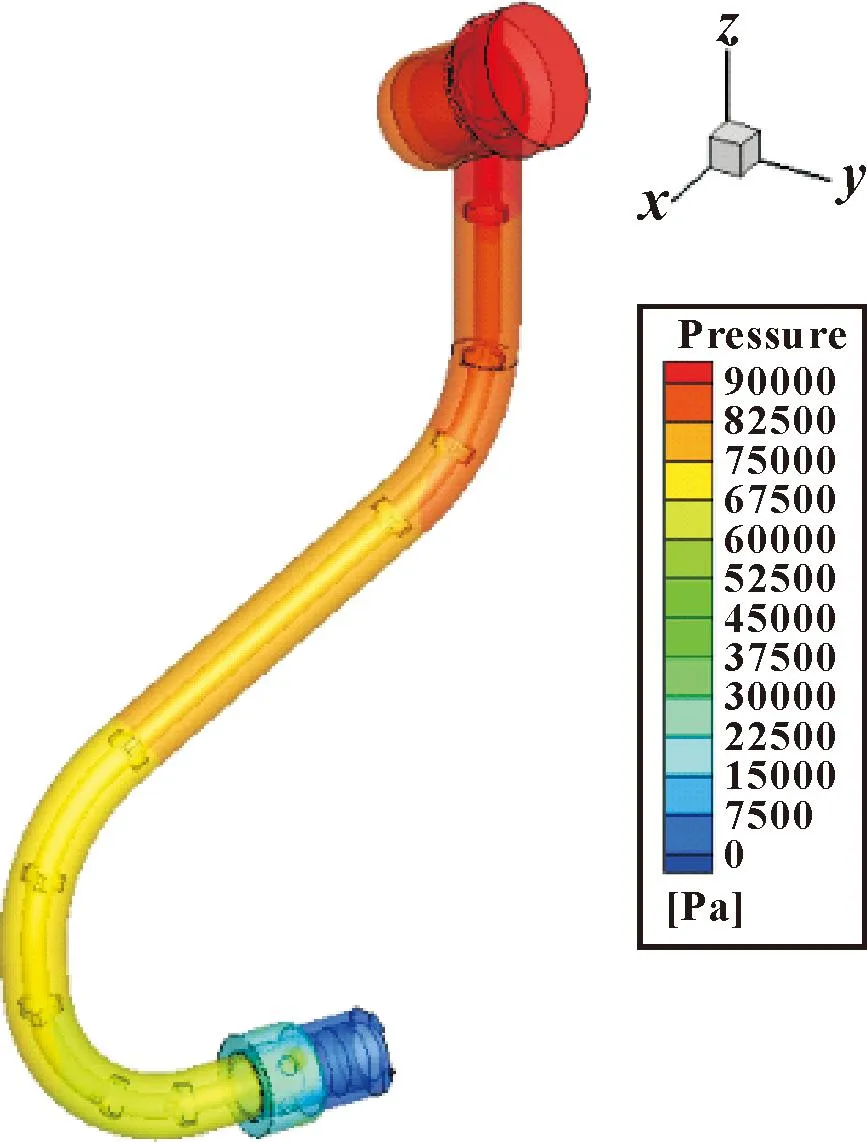
图9 主油路油管内流体流动与压降

2 预测模型建立

2.1 理论模型框架

在获知喷嘴内部结构尺寸参数以及液体压降等参数后，基于机械能守恒定律，建立燃油喷嘴流量理论模型框架。由于实际流体具有黏性，在有内摩擦力作用时，会存在机械能损失，即阻力损失hf，守恒式如下：

(4)

式中：p1为上游截面处压力；p2为下游截面处压力；ρ为燃油密度；u1为上游截面处燃油流动的平均速度；u2为下游截面处燃油流动的平均速度。

由于燃油的黏性以及几何的突变，在流动过程中发生沿程损失以及局部阻力损失，对于文中所涉及的关键几何部位，阻力损失大小表示如下：

(5)

式中：ζ为阻力损失系数。

对于其他部位的局部阻力损失以及油管等部位发生的沿程损失，通过近似直管的阻力损失表示为

(6)

式中：λ为摩擦因数。

其中，计算沿程阻力损失时，l代表直管(如油管长度)的长度；在计算局部阻力损失时，l代表管阀件当量长度，通过数值计算或查表确定。摩擦因数计算式为

(7)

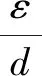
2.2 系数的确定与理论预测模型的构建

在主油路底杯处，由于突缩突扩结构，主要发生局部阻力损失。首先对于由宽通道突然收缩到窄通道的阻力系数ζ来说，公式为

(8)

对于由窄通道突然扩张到宽通道的阻力系数来说，公式为

(9)

因此，对于由宽通道经过中心孔再次扩张到宽通道的主油路底杯来说，阻力系数公式为

(10)

式中：Ahole为主油路底杯中心孔截面积；Ain1为中心孔前的宽通道截面积；Aout1为中心孔后的宽通道截面积。

同理可得到涡流器阻力系数公式：

(11)

式中：Ain2为涡流器前的宽通道截面积；Aout2为涡流器后的通道截面积；Acao1为涡流器斜槽的截面积。

对于副喷口前端处，该处结构发生了两次明显的阻力损失：

(12)

(13)

式中：Ain3为副油路喷嘴前部宽通道截面积；Acao2为副油路喷嘴前部斜槽截面积；Aout3为副油路喷嘴前端出口外圆环截面积；Acao2-out3为副油路斜槽面积与副油路喷嘴前端出口外圆环截面积之差。

通道截面积是影响阻力损失系数大小的关键参数，为了得到具有拓展性的预测模型，建立关键部位几何参数(表1)与通道截面积之间的关系。

主油路底杯中心孔截面积Ahole的计算公式为

(14)

主油路涡流器斜槽截面积Acao1的计算公式为

(15)

副油路喷口斜槽截面积Acao2的计算公式为

(16)

在确定阻力损失系数与几何参数之间的关系后，根据质量守恒方程式qv=Au以及机械能守恒式，建立燃油流量与几何参数之间的关系并计算压力损失系数余量。

主油路底杯中心孔处的压力损失系数余量ξ1的计算公式为

(17)

式中：qv1为主油路底杯流量；Δp为压降。

涡流器的局部压力损失系数余量ξ2的计算公式为

(18)

式中：qv2为通过涡流器的流量。

副油路喷嘴前端出口处的局部压力损失系数余量ξ3的计算公式为

(19)

式中：qv3为副喷口流量。

通过代入数值计算结果，得到ξ1=0.582，ξ2=4.867 4，ξ3=0.7。

接着利用上述方法，进一步得到喷嘴所有部位的阻力损失以及局部压力损失系数余量后，整合建立了整个燃油喷嘴的流量预测模型，公式如下：

(20)

式中：ξ4为主副活门内芯等其他部位压力损失系数余量；lother为主副活门内芯等其他部位的当量长度；Aother为主副活门内芯等其他部位的窄通道截面积；Ain为主、副油路同时工作时，主副油路入口截面积之和；Aout为主、副油路同时工作时，主副油路出口截面积之和；qv，othor为主副活门内芯等其他部位的流量；qv为主、副油路同时工作时总流量。

以上参数均由数值模拟确定，为定值。

2.3 流量预测模型计算结果验证

为了验证理论预测模型的准确性，通过对不同实验样件(几何参数如表4所示)进行实验测试并与计算结果进行对比，以验证预测模型的准确性。得到的对比结果如表5所示。

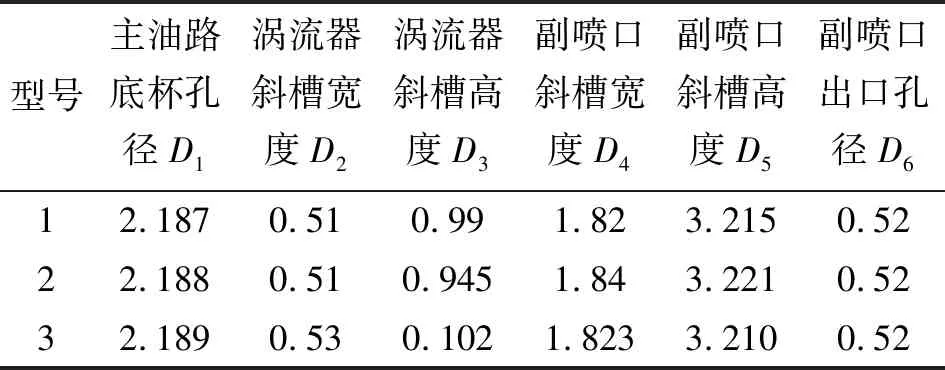
表4 实验样件关键几何参数 单位：mm

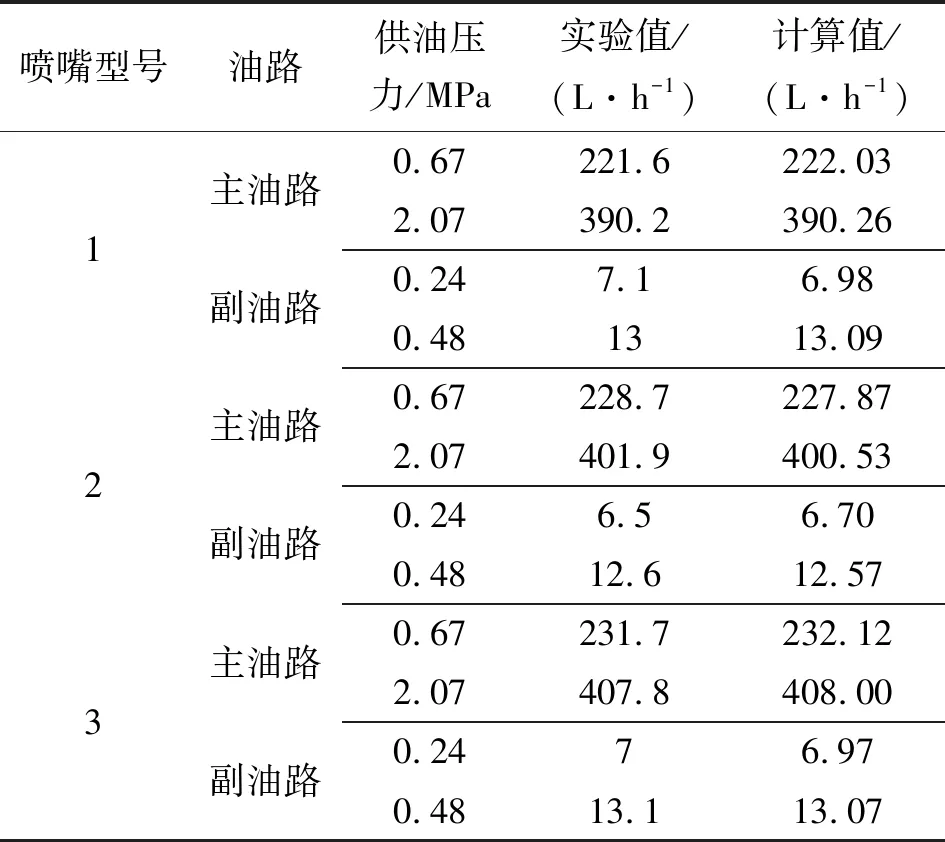
表5 数据对比

可以看到，实验结果与理论预测结果吻合较好，说明了预测模型所计算得到的喷嘴流量是准确可靠的。

3 结论

(1)燃油在喷嘴油管等部件中，主要因为管壁摩擦而发生了明显的沿程阻力损失。在活门开启截面、涡流器、主油路底杯以及副油路喷嘴前部，由于截面积的突变，发生明显的局部阻力损失。

(2)推导得到的流量理论预测模型，计算结果与实验数据吻合较好，可供具体工程参考。