pL级微量胶液转移分配过程的路径规划方法研究

李福选，刘慧芳，2，蒋申彗，陈曦，刘占奇，常云龙

(1.沈阳工业大学机械工程学院，辽宁沈阳 110870；2.沈阳特殊材料多能场复合加工协同创新中心，辽宁沈阳 110027；3.沈阳金锋特种刀具有限公司，辽宁沈阳 110027；4.沈阳工业大学材料科学与工程学院，辽宁沈阳 110870)

0 前言

随着微电子和微机械领域的不断发展，对微系统组装技术的要求也越来越高[1-2]。其中，超微量点胶作为一种粘接技术，主要是用pL级或fL级的流体来实现连接的。并且，因其对工作环境要求低、实现简单、应力低等优点被广泛应用[3-5]。但是，在面对大批量生产和多个待点胶目标时，点胶系统的移液针需要按顺序移动至各个待点胶位置，会产生大量重复的行程，大大增加了超微量点胶的工作时间。因此，迫切需要一种既能保证点胶的准确性又能优化点胶路径的方法，以满足微电子封装中超微量点胶准确性和快速性的要求。

现有点胶机在面对多个待加工点位时，都是按照沿X轴或者Y轴方向加工。若既定的加工点位排列较为整齐，按照上述方法加工还较为高效，但在实际生产中大量的待加工点位无序排列，若还按照这种方法加工将会产生大量重复行程，导致点胶的效率降低，因此需要采用智能算法对点胶路径进行规划。微量点胶的路径规划可以看作是组合优化问题[6-7]，加工路线的数量会随着待加工点位的增加而增多，在大量的可行解中寻找最优解，常规算法就显得捉襟见肘。例如，遗传算法和模拟退火算法就存在可行解构造困难、容易陷入局部最优的问题[8]。马俊等人[9]提出采用蚁群算法进行点胶路径规划，但蚁群算法较为依赖初始信息素的分布且初始状态下信息素分布较为匮乏，导致前期收敛较慢且具有盲目性，影响点胶的效率。本文作者采用改进后的遗传-蚁群算法来进行路径规划。同时，随着智能技术的快速发展，部分学者提出通过搭建视觉系统进行工件的定位工作[10-12]。因为文中的微量胶液转移分配实验是基于三轴驱动平台进行的，所以采用高分辨率工业相机进行图像采集、处理和模板匹配等操作完成定位，并通过改进的遗传-蚁群算法进行路径规划，在胶滴体积达到pL级别的同时能够快速准确地规划出胶液转移路径，既保证了微量胶液转移的准确性又能提高效率。

1 pL级微量胶液转移平台搭建及胶液转移方式

1.1 微量胶液转移平台搭建

在微电子器件生产过程中，通常会用微量胶液转移技术对精密器件进行封装处理。由于精密器件的封装对微量胶液转移技术的出胶量和位置精度都有较高的要求，而目前常见的胶液转移系统并不能达到相应使用要求。因此，需要搭建满足封装要求的微量胶液转移平台。有学者指出自动喷涂平台通常由机器视觉系统、喷涂系统和驱动系统组成[13]，所以本文作者搭建的微量胶液转移平台主要包括机器视觉系统、胶液分配系统和驱动控制系统。其中，机器视觉系统用来观察胶液转移过程及采集实验数据，由CCD工业相机、长轴镜头、同轴光源、图像采集卡和上位机共同组成[14]。胶液分配系统将胶液从共体表面转移到受体表面，由移液针、储胶管、基面组成。驱动控制系统控制胶液分配系统的运动轨迹，由X、Y、Z轴精密驱动平台和上位机控制系统组成。拟搭建的微量胶液转移平台如图1所示。

根据拟搭建的微量胶液转移平台，结合实际应用要求：机器视觉系统选用CCD工业相机、4K变焦镜头组、配套同轴光源；胶液分配系统选用直径数百微米的钨针、内径0.8 mm的玻璃毛细管、载玻片；驱动控制系统选用神津精机驱动平台、常规性能计算机、精密微驱动控制装置。实际搭建的微量胶液转移平台如图2所示。

图2 微量胶液转移平台实物

1.2 微量胶液转移方式

胶液在转移过程中按照供体表面与受体表面是否接触分为接触式胶液转移和非接触式胶液转移两种[15]。由于接触式胶液转移具有胶液分配量可控和适用胶液黏度范围广的优点，本文作者采用一种基于表面张力的超微量针转移接触式胶液转移方法，并通过机器视觉和遗传-蚁群算法对其进行路径规划。针转移式胶液转移方法由取胶、挤压、拉伸及成胶4个阶段组成，如图3所示。

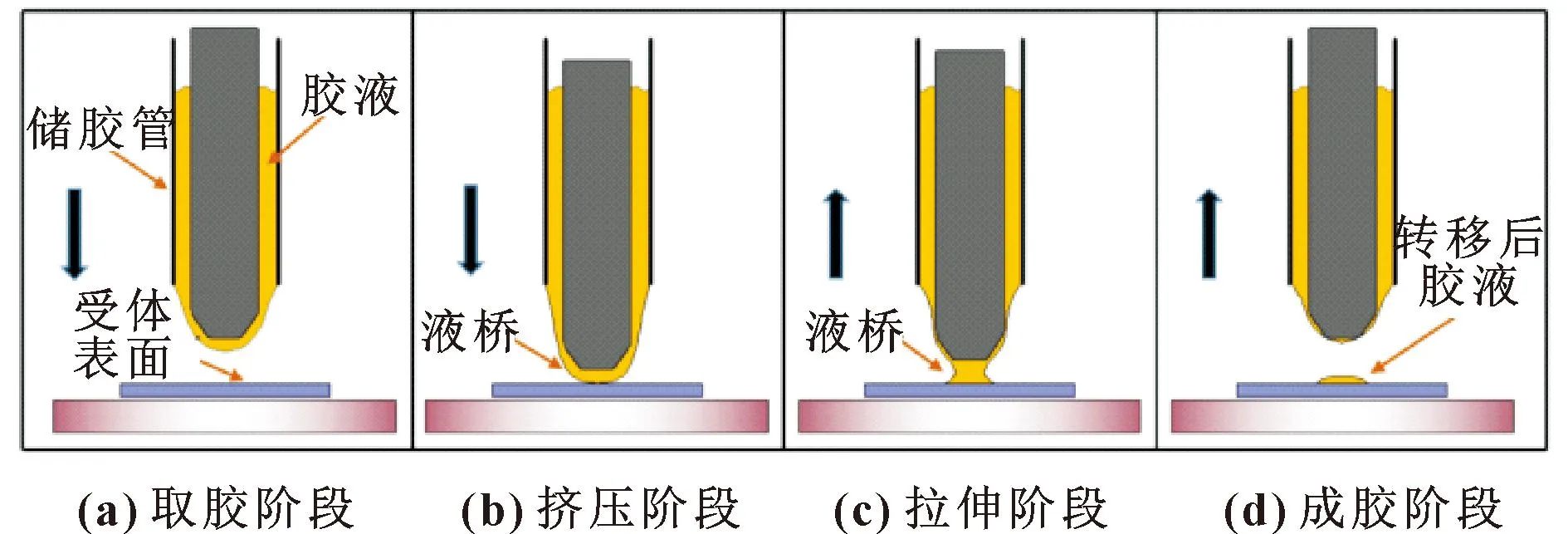
图3 胶液转移过程

通过移液针将储胶管中的胶液附着在其表面，然后通过移液针的向下移动使附着在移液针尖端的胶液与受体表面接触并将部分胶液留在受体表面形成胶滴，完成一次胶液转移。在本文作者所搭建的平台中，移液针固连在Z轴上，XY平台上放置待加工工件，移液针通过Z轴电机进行上下运动完成胶液转移工作。实际胶液转移过程如图4所示。转移后胶滴直径为微米级，体积为pL级，满足微量胶液转移分配的实验要求。

图4 胶液实际转移过程

本文作者进行路径规划的目标是位于同一平面的一个个离散的点，微动平台的XY轴根据规划后目标的顺序，将工件移动到相应位置停下，等待Z轴运动带动移液针向下进行胶液转移，待Z轴向上离开工件后，XY轴继续带动工件运动到下一个点位，如此反复直到完成作业任务。因为是离散的点且不需要连续走过多个点位，所以本文作者对于X、Y、Z轴均采用给定速度的线性插值方法，如公式(1)所示：

q(t)=a0+a1(t1-t0)

(1)

其中：q(t)表示插值后的曲线；a0表示初始时刻的位置；a1表示速度，是一个给定的常量；t0表示初始时刻；t1表示到达下一位置的时刻。

当给定速度a1后，可通过公式(2)求出a0和t1。

(2)

2 pL级微量胶液分配路径规划方法

为了将胶液分配到既定位置，常将移液针的运动路径按照沿X方向或Y方向进行规划，但是采用这种方法会使胶液转移效率降低，因此需要采用智能算法对移液针的运动路径进行规划并通过视觉系统加以辅助定位，实现准确高效的自动胶液转移分配。在微量和超微量胶液转移过程中，需要准确快速地规划出移液针运动路径，所以要求智能算法的求解速度快、稳定性较好。本文作者提出了改进的遗传-蚁群算法，利用遗传算法前期收敛快和较强的全局搜索能力，快速得到蚁群算法的初始信息素分布，改善蚁群算法初始化速度较慢、搜索时间长的缺点。同时，引入了择优和排名因子来扩大优秀蚂蚁的优势，避免蚁群算法后期陷入局部最优，使其能够稳定和快速地规划出所需路径，降低微量和超微量胶液转移分配所需的时间。

2.1 改进的遗传-蚁群算法原理及流程

路径规划应用于微量胶液转移分配的实质是对大量待加工位置进行规划，找到一个最优的加工路线，从而提高点样的效率。由于微量胶液转移分配过程是对一个个点位进行加工，所以本文作者采用十进制编码法对点位进行编号。将遍历路径总长度的倒数作为适应度函数来区分路径的好坏，如公式(3)所示：

(3)

其中：d(ci,ci+1)表示某一段路径的长度，共有n段路径。

算法中的比例选择方法采用轮盘赌法，交叉变异操作采用顺序交叉法和两点互换变异方法。

选取遗传算法适应度较高的若干优秀解转化为蚁群算法的部分初始信息素值，如公式(4)和(5)所示：

(4)

(5)

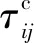
改进后的信息素更新规则将每只蚂蚁所搜寻到的胶液分配路径长度从小到大进行排列，只取前20%的蚂蚁释放信息素。同时，引入一个因子使排名越靠前的蚂蚁释放的信息素越多，扩大优秀蚂蚁的优势。该因子的数值与入选蚂蚁的排名有关，随着排名次序从1到0线性递减，排名越靠前，该因子数值越大。若某次迭代中，最优个体的路径长度大于目前已经找到的最优路径长度时，为保证之前的最优路径在被超越之前不被遗忘，将最优路径的蚂蚁作为第一名加入到排名当中，并将其他蚂蚁的名次依次顺延。最后进行全局信息素更新，如公式(6)和(7)所示：

(6)

(7)

改进的遗传-蚁群算法流程如图5所示。

图5 改进遗传-蚁群算法流程

2.2 算法初始参数选择

融合后的遗传-蚁群算法拥有许多初始参数，合理选择参数可以提高算法的性能。目前每个参数的选择没有确切的标准，主要依靠经验选择。这些参数都有一个合理的范围，如表1和表2所示。

表2 蚁群算法参数取值范围

本文作者针对的是pL级微量胶液转移分配的路径规划问题，目标数量多于50，所以蚂蚁数量初选为75。其他参数在上述范围内初选某一值，并多次调整参数，确定较优的参数组合。本文作者最终选取的参数如表3所示。

表3 遗传-蚁群算法参数

3 微量胶液转移的路径规划实验

微量胶液转移实验是对微米级的待加工目标进行胶液转移分配。因实验条件限制，本文作者通过超景深光学显微镜和超微量点胶装置制作了含有大量无序点位的待加工模板。后续的实验都将基于这个模板进行。首先，通过工业相机对其进行图像采集，模板和采集到的图像如图6所示。

图6 待加工模板

采集到的图像需进行图像分割、降噪和形态学处理等图像预处理操作[11]，保证后续实验成功进行。预处理内容包括灰度处理、二值化、中值滤波和闭运算，其效果如图7所示。

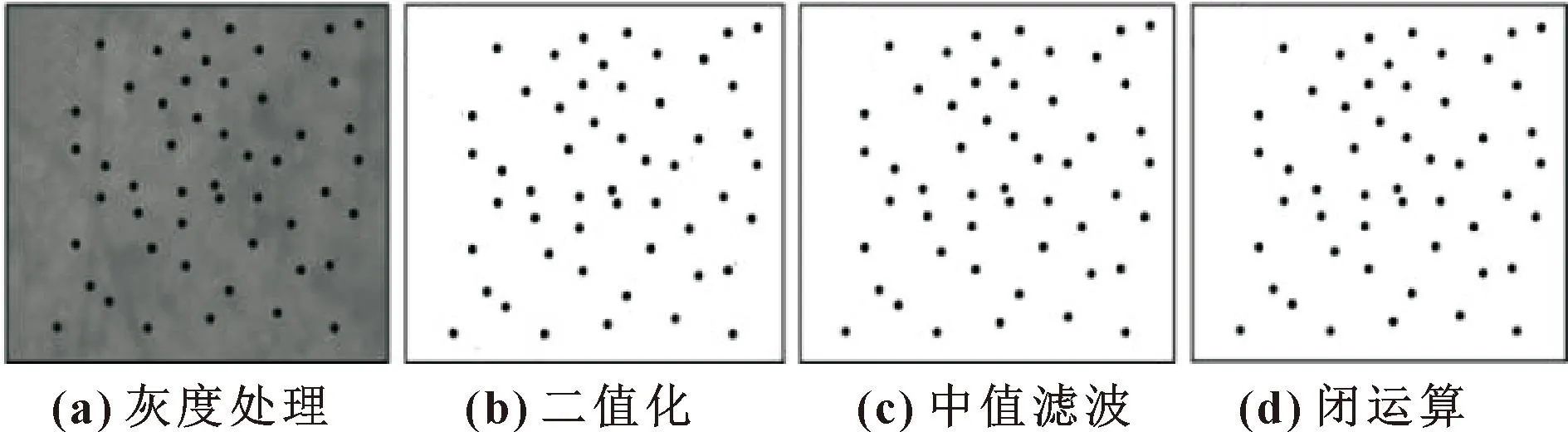
图7 图像预处理效果

预处理完成后，需要对处理后图片进行模板匹配以确定既定点位的位置信息。模板匹配是将模板图像与采集图像进行相似度对比，找到最大相似度所在区域并定义为模板成功匹配区域。由于采用单模板匹配多个目标的方式会导致边框重复，不利于位置坐标导出，因此采用NMS方式去掉重复矩形框，其效果如图8所示。

图8 模板匹配结果

将所得点位信息分别导入到遗传算法、蚁群算法、遗传-蚁群算法、沿X方向算法和沿Y方向算法得到其最优路径图，如图9所示。

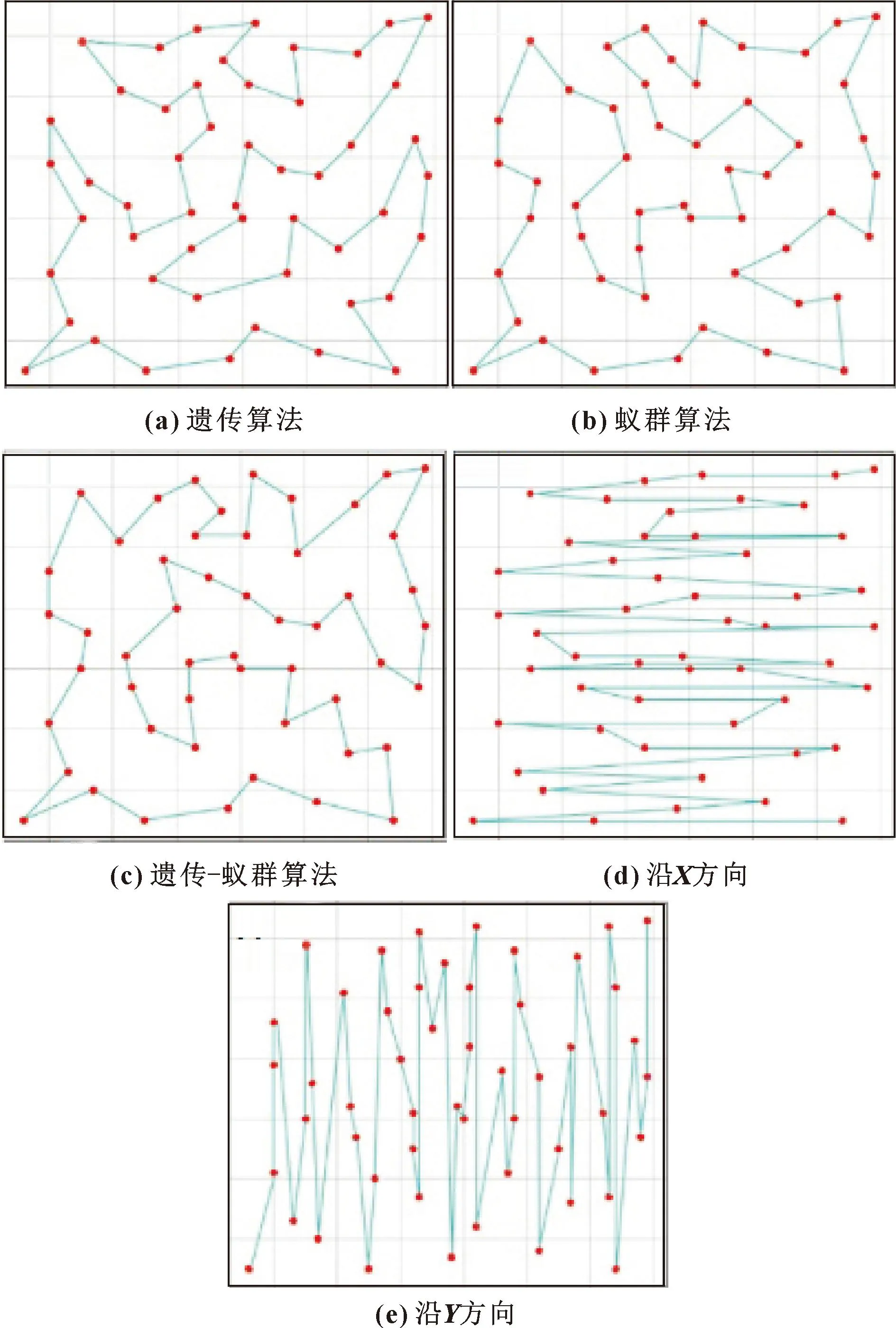
图9 规划路径

由图9可知：沿X方向算法和沿Y方向算法规划的路径有大量往复运动，经计算得出最优路径长度分别为10 900、13 360 μm；而智能算法规划的路径长度相对较短，分别为4 480、4 310、4 290 μm。路径最短的遗传-蚁群算法相较于沿X方向算法缩短了60.6%，相较于沿Y方向算法缩短了67.9%，而另外两种智能算法的路径长度与遗传-蚁群算法较接近。因此，对3种智能算法时间进行求解，得出关于路径长度和求解时间的结果如表4所示。

表4 智能算法结果

由表4可知：遗传算法的路径长度和求解时间最长，而蚁群算法和遗传-蚁群算法在这两方面的差异较小。因此对这两种算法的路径长度-迭代次数进行对比，结果如图10所示。可以看出：遗传-蚁群算法的初始路径长度更接近最优解，收敛速度更快，收敛到最优解所需要的迭代次数更少。因此在微量胶液转移路径规划单次求解过程中，采用改进的遗传-蚁群算法可以更快得到最优路径。

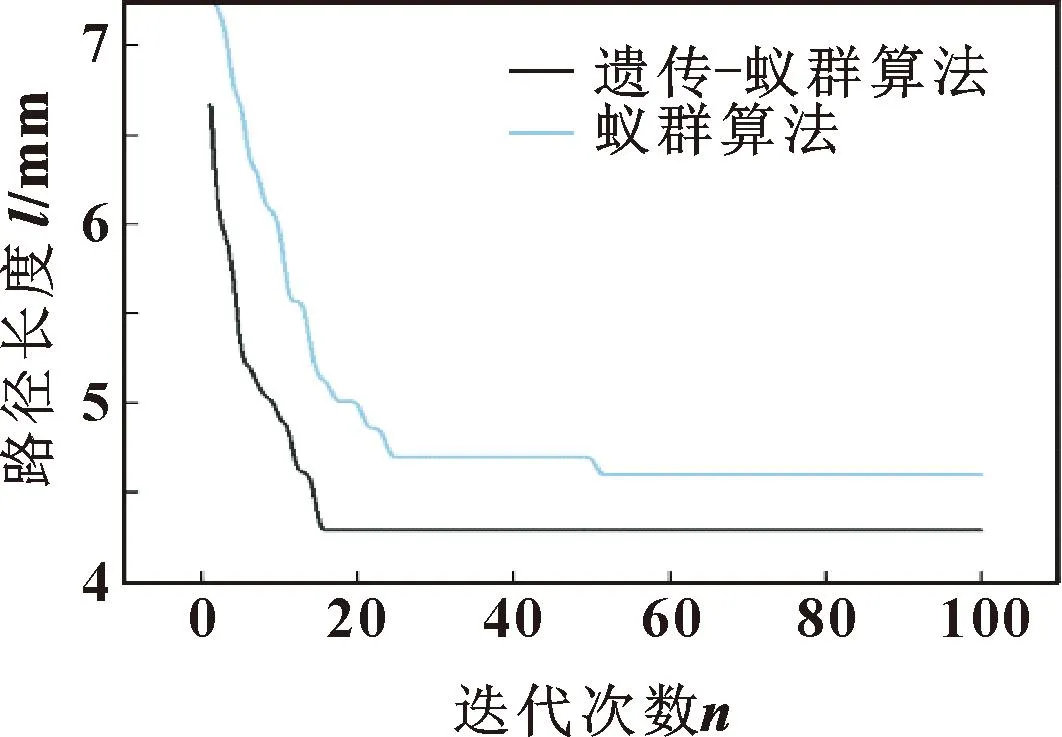
图10 路径长度-迭代次数对比

除了比较单次求解的优劣外，还需要对3种智能算法在多次求解过程中的稳定性进行对比。采用3种智能算法分别进行50次路径规划，并在每种算法中随机抽取15个样本进行比较，结果如图11所示。可以看出：遗传算法和蚁群算法的路径长度波动较大，求解稳定性较差，而遗传-蚁群算法的路径长度在最优解附近小幅波动，求解稳定性更高。

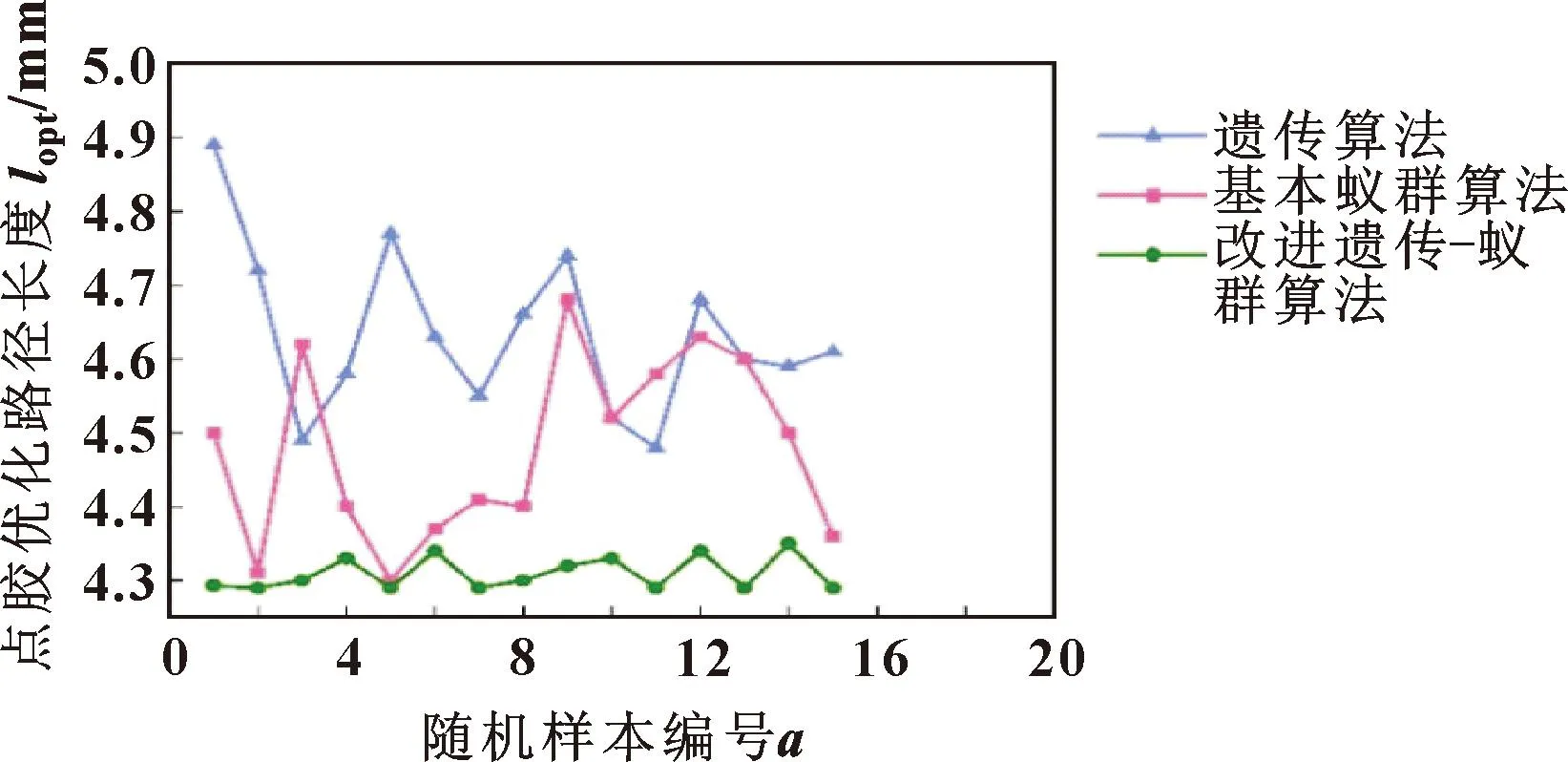
图11 多次实验随机样本图

增加待加工目标的个数再次进行多次实验，随机抽取15个样本，结果如图12所示。可以看出：改进后的遗传-蚁群算法依旧表现良好，所得优秀解靠近最优解，不易陷入局部最优且稳定性相对较好。

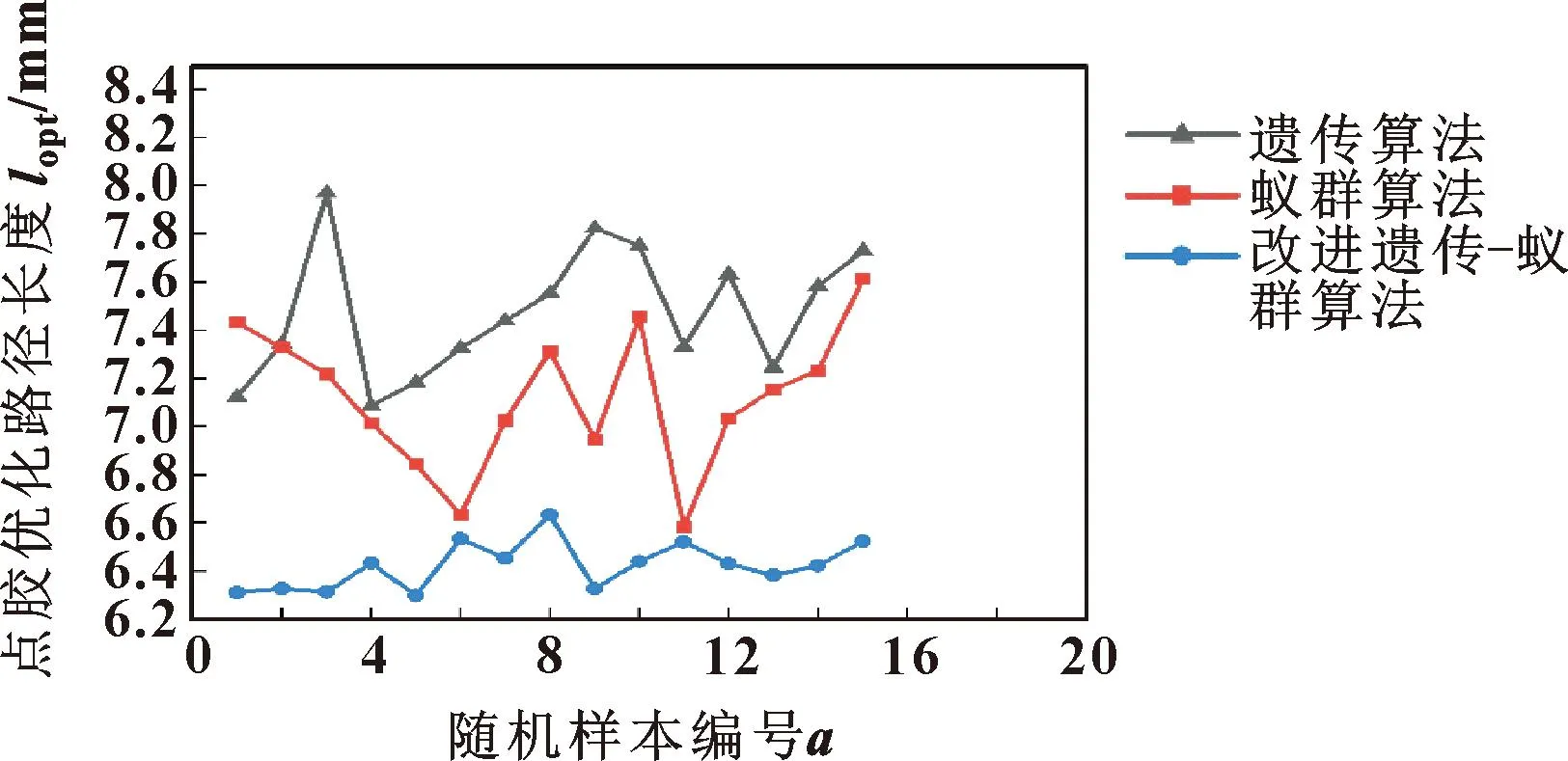
图12 增加目标后多次实验随机样本图

路径规划后会生成一系列按加工顺序排列的位置坐标，将其导入驱动控制系统中后，精密驱动平台会自动按点位顺序进行移动并配合胶液分配系统完成微量胶液转移分配，结果如图13所示。通过观察转移后胶滴和预设路径可以看出每个胶滴都落在了预设路径的节点上。驱动控制系统和胶液分配系统按照该路径花费136.8 s完成微量胶液转移分配工作，而按照传统的沿X或Y方向则需269 s或318.2 s，大幅度减少了微量胶液转移分配所需时间。

图13 微量胶液转移实验结果

通过超景深光学显微镜观测单个胶滴的形态，如图14所示。转移后胶滴完全覆盖待加工目标，其中心点几乎与待分配目标的中心点重合，位置精度较高，误差产生原因跟系统误差以及胶滴在胶液转移过程成胶阶段产生收缩有关。

图14 显微镜检测结果

胶液转移分配的时间长短除了与规划后路径的质量有关外，移液针的上下运动速度和在目标位置停留的时间也直接影响作业效率。转移后胶滴的直径也受这两个因素的影响，速度过快或者停留的时间太短都会使胶滴的直径不稳定，影响胶液分配的效果，过慢又会直接增加作业的时间。文中加工后所有胶滴直径如表5所示。根据表5可计算出胶滴的平均直径为68.6 μm，方差为0.23，波动较小，满足正常作业要求。波动原因也跟储胶管中的胶液含量有关，后续可尝试添加传感器进行胶液体积分配方面的研究。

表5 转移后胶滴直径

4 结论

本文作者通过机器视觉系统和遗传-蚁群算法解决了pL分辨率的微量胶液转移分配路径规划问题，利用机器视觉系统辅助定位加上改进的遗传-蚁群算法快速、准确和稳定地规划出路径，使转移后的胶滴几乎精确落在预设点位上，位置精度较高。胶滴平均直径为68.6 μm且波动范围较小，体积达到pL级。规划后路径相较于沿X方向规划缩短了60.6%，相较于沿Y方向规划缩短了67.9%，整个作业时间相较于传统方法减少了近半，大幅度提高了工作效率，且随着点位数目增多，文中算法依旧表现良好。