土石坝渗透分析方法综述

何义江，戴长雷，*，孔维健，张一丁

(1.黑龙江大学 水利电力学院，哈尔滨 150080；2.黑龙江大学寒区地下水研究所，黑龙江 哈尔滨 150080)

土石坝因其独特的工程建造特点而在水利工程建设中被广泛应用，在2013年，由于黑龙江省气候异常，发生罕见的特大洪水，致使黑龙江干流多处堤防工程的水位超过警戒线，其中八岔段就发生了严重的溃坝事故，致使下游大量良田被淹没，造成严重经济损失[1]。因此，对渗流问题的研究是预防溃坝等重大安全事故的重要举措。渗流是指流体在多孔介质中流动的一种物理现象。由于各种土体或岩层具有不同的物理特性和机理，不同土体中水的运动状况都不相同。由于重力或压力作用，流体在地表以下土壤或岩层孔隙中流动的过程称为渗透运动[2]，早在1852—1855年间，法国工程师达西进行大量试验得出了达西定律，该定律奠定了渗流场的基本理论。渗透试验是研究地表以下流体在土层中的水理特性以及研究流体运动情况的重要试验[3]，所以，对渗流问题进行分析时，渗流区域的水头和地下水分布特征、渗流量的计算、渗流对建筑地基的受力、渗流的速度分布，以及渗流引起的土工构筑物的变形等都是渗流研究中需要解决的问题。由于渗流的复杂性，目前渗透试验的研究方法主要分为理论方法和模型试验方法，理论方法有水力学法、有限元法和解析法等，试验方法有电模拟和水力网模型等[4]。本文介绍渗流计算的三种方法，即水力学法、有限元法和水电比拟法，分别对三种方法进行计算原理梳理和优缺点分析，为土坝进行渗流试验方法的选择提供一定的参考。

1 水力学法

水力学法求解的基础是将渗流区域内的渗流条件进行简化。水力学法是一种解析法，能得出水头、渗透流量的解析式，进而得出在流场中所求点的水头或断面流量。利用水力学法可以对浸润线的确定、渗流量、渗流坡降以及水流流速等进行近似计算[5]。

1.1 计算原理

应用水力学法时需要采用连续介质和理想液体基本假设[6]，既假设渗透系数K在同一性质土样中保持各向同性和坝体内部的水流为渐变流且通过任意过水断面的平均流速和比降保持相等[7]。在运用水力学法进行土石坝渗流分析时，关键点其一在于能够依据坝身结构、渗流特性以及坝身填筑材料将坝体进行分段，解析成简单的几何形状分开进行数值计算，其二是依据流体通过上下游断面的渗流总量相等原理建立各个几何段之间的渗流连续关系。在计算渗流量时，当渗透系数相差5倍以内时，可将该土层视为同一种土层，代替土层的厚度可由渗流量不变的原则进行加权平均计算确定。在对不透水地基的土石坝进行渗流计算时，应将整个坝体分为上游和下游，并分别计算[8]。由于上游倾斜坝坡的渗流计算要比垂直入渗复杂，因此，可将上游的三角渗流段用等效的矩形代替，如图1所示，其等效矩形的宽度可由式(1)进行计算：

(1)

式中：b为等效矩形宽度，m；m1为上游边坡系数；H1为上游水深，m。

图1 土体坝基的简化

根据式(2)即可求出上游三角段和坝身中间段合成段的渗流量。

(2)

式中：q1为合成段的渗流量，m3；H2为下游水深，m；Lx为等效矩形到下游坝坡逸出点的水平距离，m；k为坝体和坝基平均渗透系数；a0为下游坝坡逸出点与下游水面距离，m。

下游段三角部分的渗流量可以分为水面以上和水面以下两部分进行计算，根据达西定律其渗流量如式(3)：

(3)

式中：q2为下游逸出点渗流量，m3；m2为下游边坡系数；L为上游坝底下游坝底截面宽度，m；q为该土石坝渗流量，m3。

根据连续条件q=q1=q2，如式(4)。联立式(2)、式(3)和式(4)即可求出下游逸出点和该土石坝的渗流量，浸润线方程便可根据式(5)相应求出。

(4)

(5)

式中：y为坝体浸润线横坐标；x为坝体浸润线纵坐标。

若该坝型位于透水基层中，由于坝体和坝基渗透系数不同，则需要按照不同渗透系数对渗流量和浸润线进行计算。

1.2 优缺点分析

在运用水力学法解决渗流问题时，前提是需要对坝体渗流条件进行一系列简化，假定流体充满整个土壤中孔隙部分，既将渗流场看成是一个连续体，就可用高等数学来分析研究渗流问题。该方法具有计算简单且适用范围广等特点，能够解决工程实际中大多数渗流问题。运用水力学法研究渗流问题往往借助渗流模型，渗流模型不需要考虑渗流在土壤中的具体渗流路径，只需要考虑主要的渗流方向，但是其不足之处在于其求解出的渗流要素是仅为截面的平均渗流要素，无法求出流场内任一点的渗流要素，且该法在计算时进行的基本假设与实际存在差距，故求解结果往往会出现误差[9]。

2 有限元法

20世纪40年代初，德裔美国数学家Richard Courant首次提出有限元方法。在处理复杂问题时，将连续求解区域分解成若干子区域，对子区域进行求解进而推广到整个区域的求解，即为有限元[10]，这些有限元通过有限个节点能够组合成一个等效的集合体，各有限元的连接方法和形状不同，有限元法能通过数值模拟求解非标准几何。假设每个子区域都有适当的逼近解，并由此得到该子区域整体满足条件的解[11]。有限元法的基本原理是把微分方程及其边界条件的求解转换为泛函求极值的问题，其核心原理主要分为两部分，分别为分块插值和剖分离散[12]。有限元法是目前对于边坡稳定性分析的一种常用的数值方法。

用有限元对土坝进行渗流分析的软件有很多，例如AUTOBank-slop、GeoStudio中Seep/W和ANSYS等相关软件。李保民[12]基于Seep/W对山东某土石坝进行渗流分析，探究了不同水位对坝体的渗流影响，进而对大坝的防渗加固提出建议。关万彬[13]基于二维有限元法利用AUTOBank渗流分析有限软件对西泉眼水库土坝进行渗流分析，通过准确计算浸润线和渗流状态得出一些该坝的水理参数，进而对大坝的安全评估以及相关水利工程建设提供设计依据。陈雨瑶等[14]通过对黑龙江干流溃口八岔段采用GeoStudio软件的Seep/W模块进行渗流模拟，研究不同水位下堤防能否完成挡水任务。赵俊宇[15]在学位论文中通过Seep/W模块研究非稳定渗流状态下坝体渗流场的变化，得出水库水位反复变化的速率不利于坝身的稳定性。

2.1 计算原理

有限元法是一种变分法与多项式通过插值结合的方法[16]，有限元法求解渗流问题时，是将渗流的基本微分方程和其边界条件利用变分原理变换成函数的极值求解问题，在进行有限元分析的重要基础理论是将一个连续域分解为若干个有限单元，建立插值函数的关系，将每个有限元通过节点连接[17](如图2)，通过计算机对线性代数方程的形式进行求解，有限元计算时，其计算量往往比较大，因此，一般都要借助多种计算软件，必要时还要编写相应的计算程序。用有限元进行渗流分析的大致步骤如下[11]：

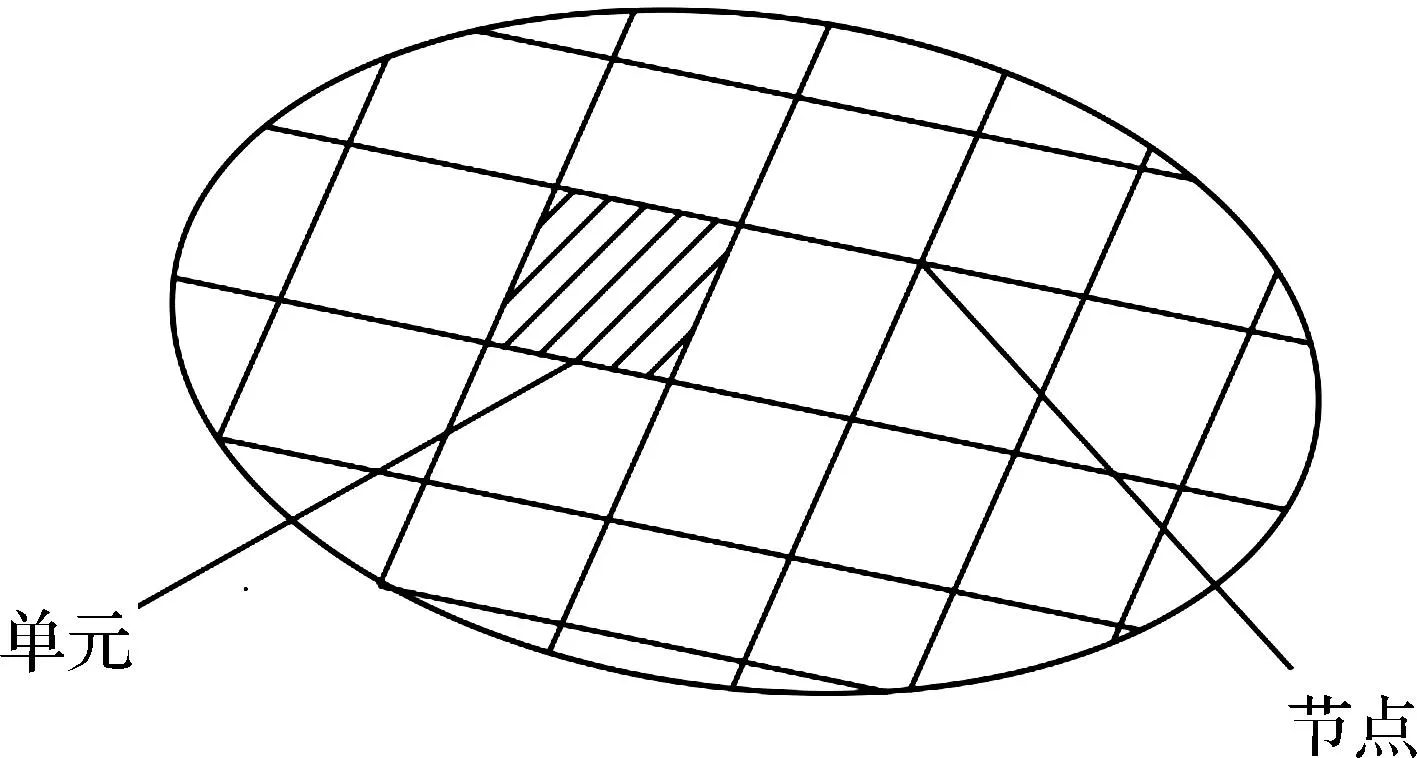
图2 渗流区域划分为若干个子区域

(1)把所研究的渗流区域分成若干个互相连接的单元。

(2)单元划分后，按照单元建立水头插值函数，分别确定每个单元的水头函数。

(3)通过变分法推导有限单元方程，建立单元渗流矩阵。

(4)将各单元的单元矩阵集合形成整个渗流区的总的渗流矩阵。

(5)求出各节点的未知水头值。

(6)由节点水头值计算水力坡降和渗流量以及其他的水理参数。

2.2 GeoStudio中SEEP/W渗流模块

SEEP/W是加拿大GEO-SLOPE公司GeoStudio系列软件[18]，该软件的主要目的是模拟地下水渗流分析。它是一种有限元软件，用于分析土壤等多孔透水材料中的地下水渗流等水力试验。该软件在有限元的基础上，能够对土石坝体非饱和条件下孔隙水压力进行分析，同时，还可用于分析边坡在稳定状态下的瞬态孔压，在此基础上，通过对孔隙内水压力的时序分析，得到了渗流场、浸润线、渗流流速、水力坡降等水理参数。在此基础上，进一步研究边坡和坝堤随时间变化的稳定性。由于该模块的强大的渗流计算功能，从而能够分析不同工况条件下的渗流情况，得到较为清晰的计算结果，该软件目前在水利工程建设以及矿产行业等其他领域中已被广泛应用。

2.3 优缺点分析

有限元是近几年出现的一类新的数值方法，它可以处理非均质、各向异性等复杂边界条件，是目前国际上应用最为广泛的一类渗流计算方法，它有很好的适应性和很高的精确度等特点，对于复杂地基上的大型水利枢纽工程，一般都会使用有限元法来解决渗透问题。采用有限元方法的优点在于它具有较强的计算灵活性(既可为离散空间，也可为基函数)。但有限元法是一种比较复杂的数值方法，虽然该方法可应用于不规则区域，但是对区域的连续性等要求比较严格，且计算工作量很大，必须依靠计算机辅助[19]。

3 水电比拟法

水电比拟法又称水电模拟法，水电模拟试验即通过研究电场中电流的运动来模拟地下水运动过程，从而研究渗流问题，我们称之为水电比拟[20]，巴普洛夫斯基在1918年的首次提出了水电模拟，并在20世纪20年代将其用于土壤和大坝渗流问题研究[2]。该模型的理论依据是基于渗流方程和电学方程在数学表达式上具有相似性而建立相关性，利用电场模拟多种情况下的渗流场[21]。水电模拟试验在水力学问题中应用比较普遍，是研究地下水运动的重要方法，不仅可以研究地下水渗流运动，还能研究地表水运动的问题。随着水电模拟试验技术的不断发展，它已从解决单一介质中的流动问题扩展到了解决多层介质中的液体流动的问题，同时它也已经实现了从各向同性介质的问题到各向异性介质中的问题的过渡。还可以解决多维空间条件下的渗流问题。

对于稳定流，平面渗透流问题是测量电场中电荷的等势线来比拟渗流场中的等水头线，在此基础上绘制流网研究渗流相关特性，对于无压渗流，通过测定相对电位的比值来确定浸润线，计算得到流网即可确定渗流区域的流场，进而场内的各种水理性质如孔隙水压力、渗流流速、渗流坡降、渗流量等可相继求得，依据这些水理性质便可以分析大坝的管涌现象、流沙现象等对工程安全构成威胁问题[22]。

3.1 计算原理

根据流体在孔隙介质中遵循达西定律，而流体在导电性介质中遵循欧姆定律，采用电仿真试验来进行渗流问题的研究是水电模拟试验的理论基础。在稳定的渗流中，这两个物理场可以用相同的数学方程，理论基础是相似定理，在符合达西定律条件的背景下，渗流的运动规律与导体中的电流现象规律保持一致，其表现形式可以用Laplace方程来表示(具体对比关系见表1)，因此，在模拟有压渗流电模型设计时，首先要满足几何形状条件控制边界条件的相似，以及考虑导电性质和渗透性质相似，将研究渗流场中的各种力学量转化为研究电场中的各种电学量，进而将渗流问题转换到电模型中，利用简单的测试设备得到结果，再转换为渗流区域。下表所列为渗流场和电场中各物理量的对比关系[23-24]。

表1 渗流场和电场各物理量对比关系

利用数学模型建立渗流场中达西定律与电场中欧姆定律的相似关系如式(6)、式(7)：

(6)

(7)

式中：负号表示水流沿水头流动方向或者电位的降低方向。由以上二式可以发现，渗流场中与电场中各物理量一一对应关系如表1所示，将对应物理量用模型比尺表示，令λh=H/u，λk=k/ρ，λ=s/s′，λv=v/i，则式(7)可转为式(8)：

(8)

将(8)式与(6)式和(7)式相比，欲使(8)式与(6)相等可得以下关系，如式(9)：

(9)

当模型比尺=1时，即如水工模型水力学相似律中模型与原型的弗劳德数比值或雷诺数比值=1。由式(9)可得，当模型电阻参数确定时，则只能改变电压或电流密度，两个变量确定一个，另一个变量也相继确定。

由于渗流场和电场的介质参数具有相似性，在模拟均匀介质时，导电介质可以任选的前提是保证电导率和渗透系数保持固定比值，在模拟非均匀介质时，两场中各层的对应参数应满足以下关系，如式(10)：

(10)

式中：k1…kn为渗透系数；σ1…σn为导电率。

根据相似理论，若两个数学模型相似必有相似解，这样就可以在建立相似基础上的模型装置研究渗流问题，通过测定电场来求解相对复杂的渗流规律问题。

3.2 优缺点分析

利用水电模拟试验研究渗流运动相较于其他模型试验具有较强的优越性，例如在利用沙模型研究液体渗流时，沙子本身的粗细程度难以保障以及沙模内部渗流情况也难以捕捉，导致工作量很大。还有一种模型如黏性液体模型在做层流模拟试验时，很难保证液体的黏度，并且模型边界条件稍改变就会导致测量结果不精准。而电模拟在研究渗流问题时，所具有的优点可总结如下：

(1)该模型的设备较为简单，使用电子仪表进行测试也较为方便，且测量精度较高。

(2)比较好控制边界条件，可更好控制单一变量的改变。

(3)准确迅速，工作量较小。

(4)能够更好地模拟坝体内渗流问题，仿真效果较好。

4 结 论

(1)在运用水力学法解决渗流问题时，其优点是通过构建水利模型计算结果比较符合工程实际，计算比较简单，但是在计算时需要做出一些基本假定，且计算结果不是很精准，是一种近似解法。

(2)在用有限元进行分析渗流问题时，可以处理一些坝体边界比较复杂的边界条件，适应性较强，计算结果精度高，但是，这种方法的计算工作量很大，要借助计算机的帮助来实现。

(3)在进行水电模拟试验来研究坝体渗流场问题时，试验操作简单，由于相似原理，能够更好地模拟坝体内渗流问题，通过观察电荷运行情况能更好地模拟坝体内液体渗流情况，其缺点是进行该试验需要专门的设备，且调制设备过程较复杂，后期工作较多。