农村集中供水工程规模与结构协调优化研究

高 静，陈新美

(1.邯郸市复兴区润沣水务有限公司，河北 邯郸 056003；2.邯郸市水资源管理中心，河北 邯郸 056002)

1 农村集中供水工程优化模型

1.1 农村集中供水工程规模优化模型

研究项目区域内，目前农村生活用水水源为自备井，水质未经安全处理，水质、水量无保障；灌溉用水取自地表水和地下水；工矿企业用水水源包括地下水、河流汇集的矿排水及季节雨水。该区域为资源性缺水地区，且水资源较为匮乏。复兴经济开发区占地约2.3 hm2。本地区西部有煤田、铁矿等矿产资源，可为本地区提供丰富的自然矿产资源、水资源及劳动力资源。供水厂水源主要来源于两个方面，一是市区原有供水厂，但由于本地区地势较高，需加压供水，成本较高。二是利用西部矿井疏干水，自西向东至受水区。村庄现多采用自备水源，自行打井。

研究规划新建开发区供水厂，规模为0.8万m3/d，占地2.3 hm2。水厂水源为南水北调和矿井疏干水，输水管线分别沿道路敷设。为保障供水安全，开发区规划供水管网以环状网为主，环状与枝状管网相结合，供水管道在街道一侧布置。项目最大取水量为300万m3/a，全部取自中奥陶统石灰岩含水层地下水，水质水量均能满足矿区生活、生产用水需要，项目生活、生产用水水源均为帷幕内矿坑疏排水。

为了在区域农村供水工程建设中实现多水源多目标综合供水，需要确保系统上的供水工程规模合理和经济。与单一供水工程相比，这是一项具有很大不同的任务[1]。为了分析地区供水工程的合理规模，必须明确影响其规模的主要因素。农村集中供水工程建设规模影响因素如图1所示。

图1 影响因素

研究在遗传算法的基础上构建农村集中供水工程的规模优化模型。考虑到农村供水的特点和现实情况，需要确保建设片区内所有水厂、输水管网建设及运行能经济合理，确定合适的供水规模。通过分析各类供水工程建设规模的影响因素，研究构建了一个费用模型，旨在将费用之和控制到最低。因此，该模型主要考虑单位输水成本、水源建设费用和输水管道管网建设费用，以这三个变量为中心构建目标函数[2-3]。针对改造后的水厂，将改造成本视为可变因素，将已建成水源与总投资按固定值处理。假设选取区域内满足要求的水厂m个，在这其中满足要求的供水分区有n个。假设Wi为第i个水厂的最大可供水量，ai为选定的水厂在0到Wi的范围内能够采用的集中制水规模集合；Qia为第i个水厂采用制水规模a时的最大可生产能力；Ria为水厂i在采用制水规模a的情况下设置的控制范围，Fia为水厂i在采用制水规模a时所需的修建费用，qija为水厂i在采用制水规模a时向j供水分区提供的水量；Dj为分区j需水量，Lij为第i个水厂与分区j的距离，Bij和Cij分别为两者之间输水管道的建设费用和输水成本。则目标函数Z如式(1)所示。

(1)

式中：Yia为决策变量，代表第i个水厂被选中；Uij第i个水厂的第j个供水分区。为简化供水区域内供水对象众多的计算，本研究使用GIS技术进行供水区域分区及管网规模计算。结合人口密度、人口分布及地理条件等因素，通过空间聚类分析等工具对供水建设区域的布局进行划分和分析，并计算各供水区域中心距离每个水厂的距离。通过建立各分区网格以及各水厂距离的矩阵，可以高效地计算管网规模，为供水工程规划提供参考。研究采用遗传算法对农村供水工程规模优化进行求解，并且在实际算法应用中进行适当算法优化。应用遗传算法研究模型时，种群初始化时需要满足约束条件，以确保搜索的有效性。如果种群状况不符，那么种群需要再次生成直到达到规定的种群要求。一般情况下，适应度函数能够反映出种群中个体在环境中的生存能力以及优劣素质，针对研究提出的模型，对符合约束条件的个体进行评估，构造适应度函数以测算其生存能力。约束条件匹配公式(1)。优化后的遗传算法染色体表示为{o11，o12，…omn；p11，p12，…p1a1；p21，…，p2a1，…，pma1}，其中o与p均为随机数。在农村供水工程的规模化过程中，首先要以水文特征为基础，分析确定水厂的空间位置，并对已经存在的其他水厂进行数据统计。然后对该区域内供水用户进行统计，利用GIS工具处理对用水户的位置进行划分，进一步得到各分区到各水厂输水管的建设距离，计算每个分区的供水需求量。对作为备选的水厂给定一个供水需求量的最大值，从而得到最终的供水规模，将备选方案分为不同规模水平。然后，采用相关分析方法，依据供水源，建立不同村庄农村供水工程规模及费用约束方案，建立区域内的农村供水工程建设规模化的系统优化模型，以达到规模最优化的目的。

1.2 农村集中供水工程结构优化模型

为优化研究区域农村供水工程结构，建立与管网实际情况相符的模型是关键。研究模拟拓扑结构构建农村集中供水结构优化模型。首先，针对农村供水管网的dwg源文件进行处理，并将其中的图线按照不同的管径进行分层。随后，将dwg文件通过CAD转换器转换为dxf格式，以便进行下一步操作。之后使用Dxf2epa软件将dxf文件转换为inp格式，但在进行转换之前要确保dxf文件已关闭，以避免转换错误。对inp文件的基本属性进行检查，保证其与源文件对应属性一致，否则对缺失或不相符的属性进行修改，使其满足模型要求。使用EPANETH软件导入inp数据，生成最终的供水管网net文件，以便进行模型优化设计。值得注意的是，在建模过程中，应充分考虑本地区的特殊情况和实际需求，将环境、建设成本和社会效益等因素综合考虑，以达到优化设计的目的。而在建立模型后，需要进行有效性和精度的检验，以确保优化设计的可行性和有效性。同时，针对不同情况进行合理的预测和评估，以便实施后达到预期效果。拓扑结构图如图2所示。

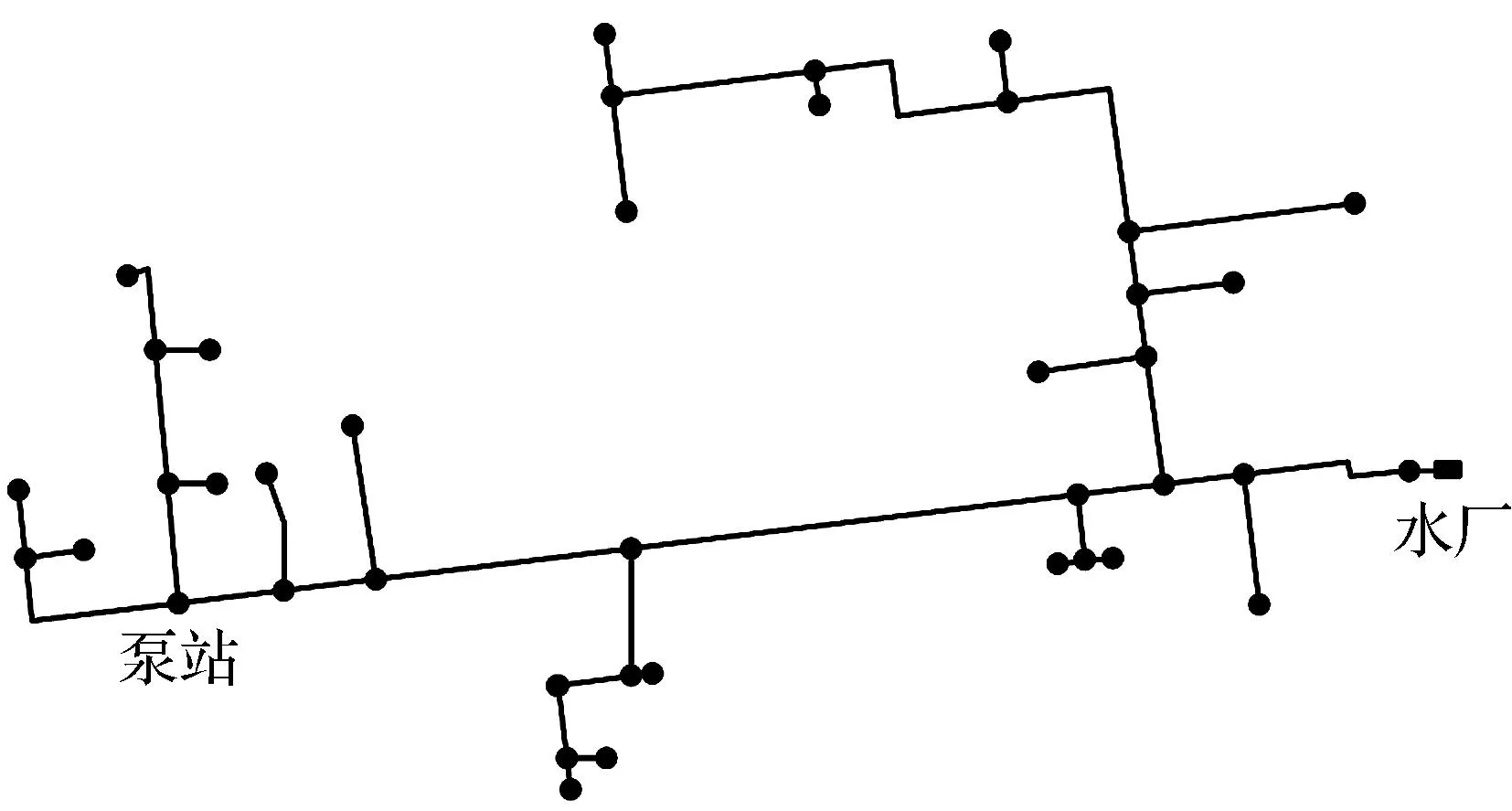
图2 拓扑结构图

图2中的拓扑结构包含水泵、管道、节点等拓扑组件，各个组件的基本属性有所区别。节点、管网和水泵数据等通过软件生成。为了进一步优化，引入“弹性”概念。弹性可以被定义为系统抵抗、吸收和承受以及从异常情况快速恢复的能力。弹性系统包括多种属性，如连接性、效率性、中心性、快速性、冗余性等。选取连接性、效率性、模块性和中心性进行指标计算并评价，形成的度量代表主要可分为四类，分别为连接密度、平均路径长度、直径和中心点优势。其中，连接性代表网络的连接密度；效率性可以通过平均路径长度来评价，其指任意一对顶点之间的平均距离。该指标与图形的直径和半径相关，因此，只选用平均路径长度；模块性代表网络中的直径，直径是最大偏心率，只能通过无线网络求解；中心性代表网络中心点优势，根据各个节点最短路径的一部分来进行求解。中间性系数的取值范围为[0，1]，具体计算方式如表1所示。

表1 指标计算方式

2 农村集中供水工程优化分析

2.1 农村集中供水工程规模优化分析

进行农村集中供水工程规模优化分析，模型计算得到的水厂规模与水厂投资金额之间的相关性曲线如图3所示。

图3 相关性曲线

从图3可以看出，水厂建设规模与投资金额是呈现正相关关系的，其中投资规模上升越到后期，投资金额的上升速度也就越快。

从表2中可以看出研究设计的模型可以有效规划水厂的改建时间和改建规模。在建设年份上，考虑工程的建设年份可以保证建成后能够满足当前和未来的供水需求。可以看出模型根据供水工程规模，进行了为期两年的供水工程的规划。在建设规模的确定中，工程性质是一个重要的因素。列表中所有的工程都是改建性规划，这意味着它们是在原有水厂的基础上进行旧厂改建或扩建，而不是新建工程。此举不仅可以节约建设成本，还能够减少土地使用和环境影响等问题。LSW水厂、KZL水厂和DSS水厂三个水厂在2021年规划建设，工程规模都为5000 m3/d，这可能是因为这三个水厂所在区域的供水需求相似，同时考虑到未来的用水量也有一定的扩展空间。另外，SC水厂、WTZ水厂、ZJL水厂、ZNZ水厂和BS水厂五个水厂在2022年规划建设，工程规模较小，可能是因为这些区域的供水需求相对较低，同时考虑到未来的用水量增长也不会太快。同时可以看出模型可以充分考虑建设成本，根据当地的供水需求来最大限度地降低建设成本，形成梯度式的规模规划。

表2 规模分析结果

2.2 农村集中供水工程结构优化分析

在农村集中供水工程结构优化分析中，研究首先通过模拟拓扑结构来对市场线路网络进行特征化分析。结构化特征分析包含供水水流流经的水库与管线运输网络，其中泵站的输送扬程规模为10 m，输送流量达到3.4 L/s，管线节点特征属性如表3所示。

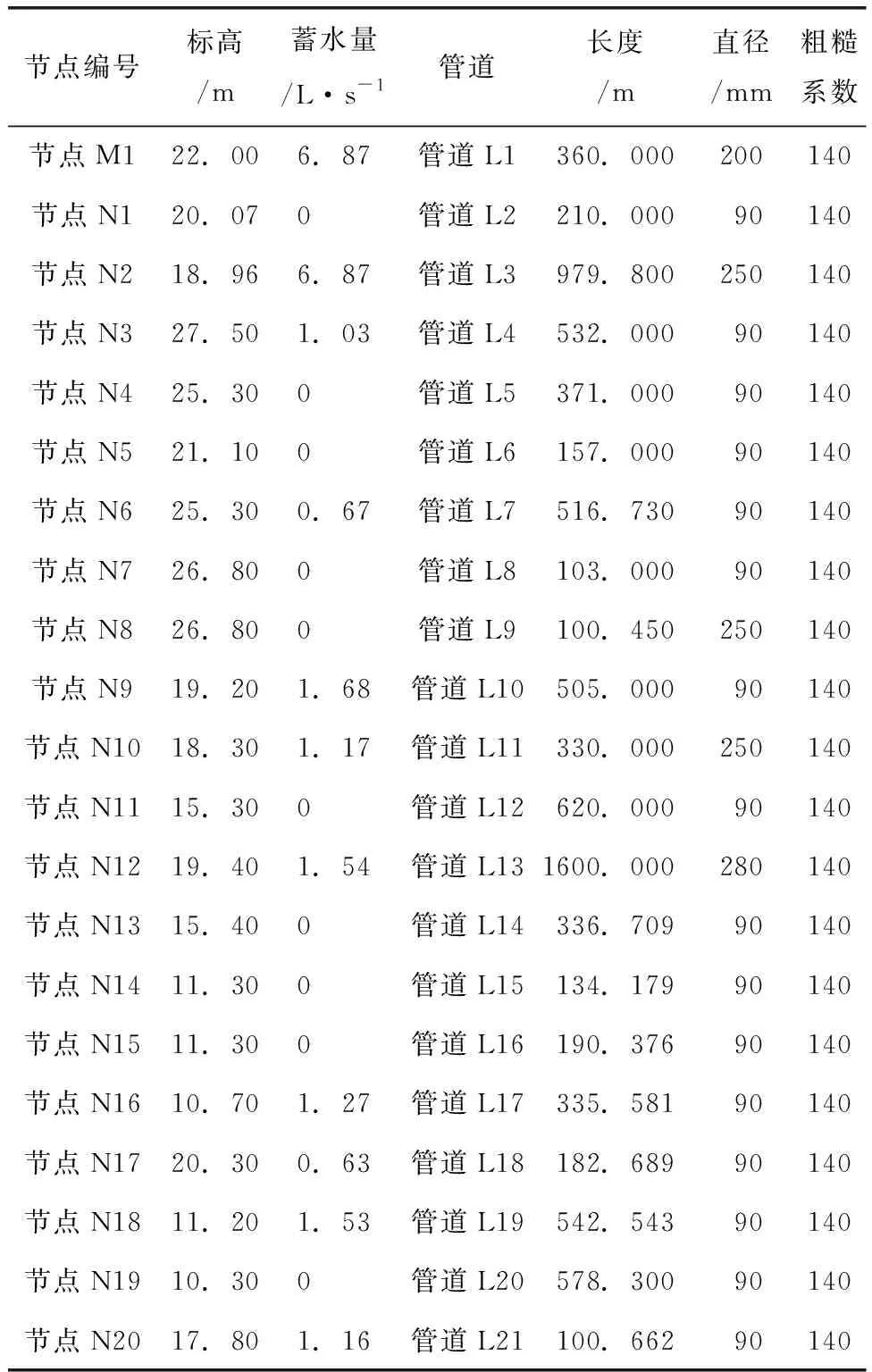
表3 管线节点特征属性

由表3可知，节点集合包括水库M1和N1到N20共计21个节点，其中水库节点蓄水量为6.87 L/s，节点N1不蓄水，而节点N2蓄水量同样为6.87 L/s，如此延续至节点N20，这些节点之间通过管道L1到L21进行连接，总长度为5446.29 m，管道直径为90～280 mm，粗糙系数为140。节点的标高在11.2～27.5 m之间，标高高低对于管道水力特性的影响非常大。节点N9的蓄水量达到了1.68 L/s，最高值是节点N2的6.87 L/s。管道长度也各不相同，从103.00 m的L8到1600.00 m的L13。这些管道的直径各异，但粗糙系数相同，这可能会对于管道的水力特性也产生一定的影响。选取节点中具有代表性的5个节点，它们的弹性分析结果如图4所示。

图4 弹性分析结果

图4(a)为受供水不足影响节点数的平均百分比，给定两个值作为节点的赤字阈值，其中较小的为20%，表示一小部分的用户供水受到影响，但是水量可满足要求；另一个是35%的严重赤字，这时大多数用户的供水都依赖于管网的供应，但是水量不足，一些用户甚至没有供水。图4(a)表现了关闭不同连接所影响的交叉口百分比示例，算例结果为37.5%，即赤字严重。图4(b)为关闭不同节点后水龄随时间的变化曲线，平均化弹性值为1.95 h。平均化学污染恢复时间如图5所示。

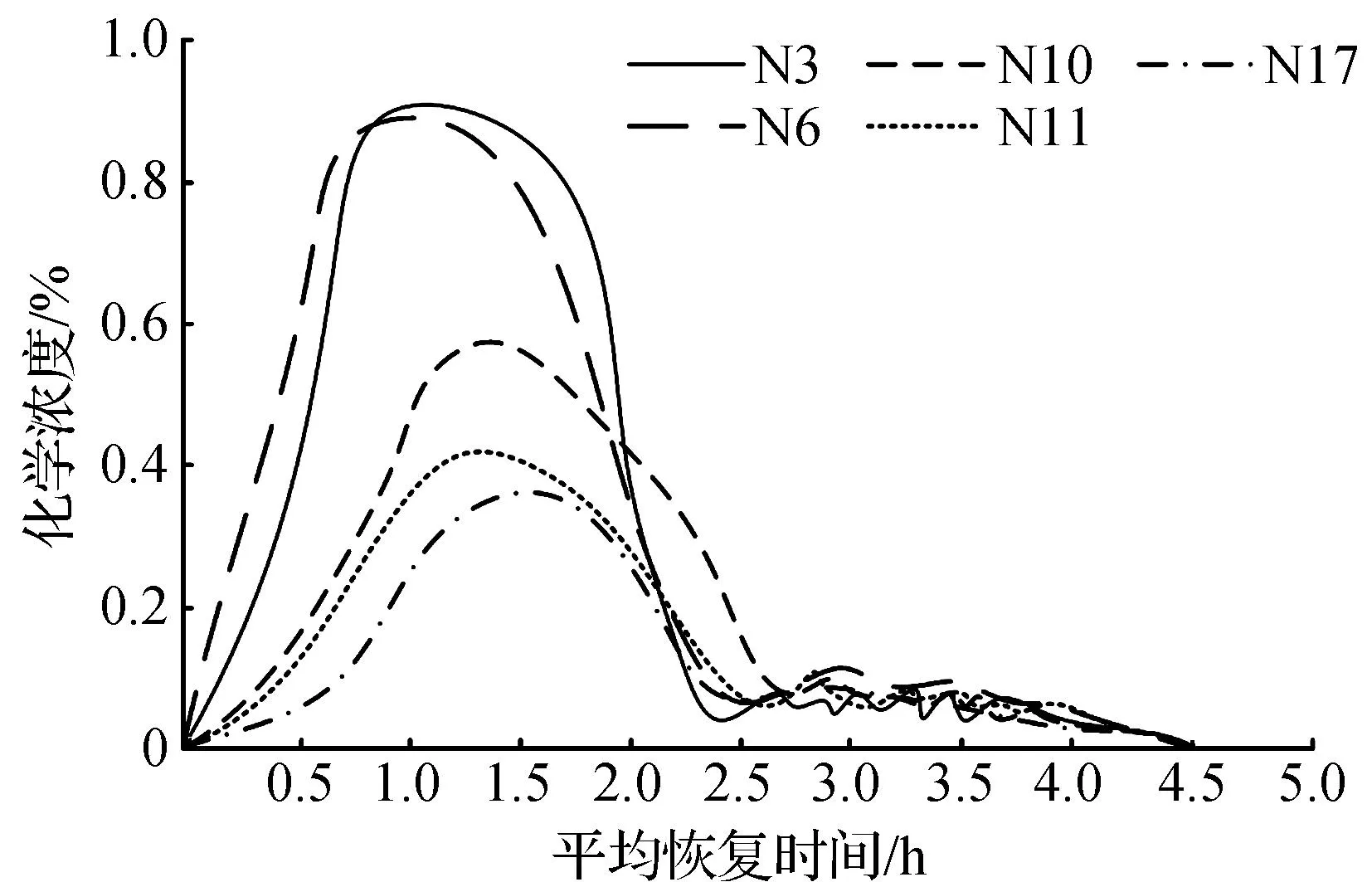
图5 平均化学污染恢复时间

通过监测连接处注入的化学品总量，可以了解管网中的化学物质流动情况。图5中每条线表示在特定连接处随着时间的推移注入的化学品总量。管网的弹性取值为4.10 h，说明在管网中的化学物质流动速度相对缓慢，需要一定时间才能达到影响整个管网的程度。

3 结 论

研究运用遗传算法等方法建立了农村供水工程规模优化模型并模拟拓扑结构，对供水水流流经的水库与管线运输网络进行结构化特征分析。研究表明，该模型能够有效规划供水工程的建设年份和规模，形成梯度式的规模规划，并且最大限度地降低了建设成本。另外，研究的拓扑分析结果显示，管网弹性值为4.10 h，可以有效地指导维修工作，平均化弹性值为1.95 h。管网的弹性取值为4.10 h。说明在管网中的化学物质流动速度相对缓慢，需要一定时间才能达到影响整个管网的程度。研究设计的方法为农村供水工程的规模优化和运行维护提供了基础性理论和实践指南。