美妙的“糖水不等式”
高 莹
(安徽省马鞍山市第二中学)
本文笔者以一道课本习题为母题,继续深入研究“糖水不等式”及其变化形式,在不等式证明、函数等问题中探索应用,旨在进一步挖掘教材习题丰富的知识内涵,为“糖水不等式”的拓展提供思路.
1 课本习题回顾
【题目】(普通高中教科书(2019版A版)必修一·43页·10)已知b克糖水中含有a克糖(b>a>0),再添加m克糖(m>0)(假设全部溶解),糖水变甜.请将这一事实表示为一个不等式,并证明这个不等式成立.
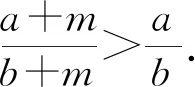
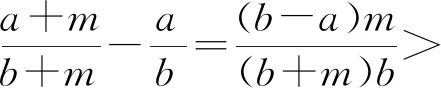

课本在复习参考题2第7题中再次应用“糖水不等式”解决生活情境中的问题.
【题目】(普通高中教科书(2019版A版)必修一·58页·7)一般认为,民用住宅的窗户面积必须小于地板面积,但窗户面积与地板面积的比应不小于10%,而且这个比值越大,采光效果越好.
(1)若一所公寓窗户面积与地板面积的总和为220 m2,则这所公寓的窗户面积至少为多少平方米?
(2)若同时增加相同的窗户面积和地板面积,公寓的采光效果是变好了还是变坏了?

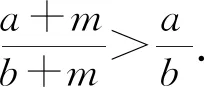
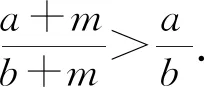
翻阅上一版人教教材(2007版A版)选修4-5“不等式选讲”第21页例2:
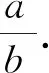
2 “糖水不等式”的一般形式
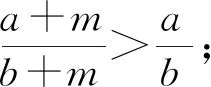
3 “糖水不等式”的证明(以若b>a>0,m>0,则为例)(这里仅列举几种常见证法)
(1)作差法
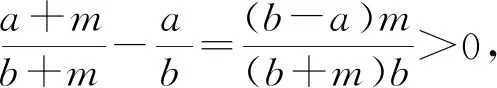
(2)分析法
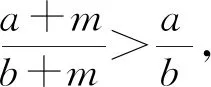
(3)综合法

(4)数形结合法
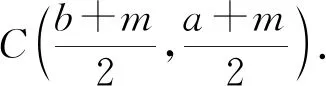
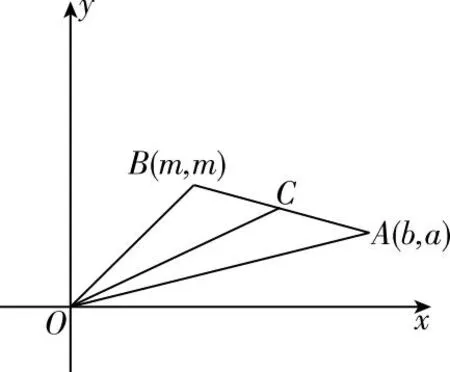
图1
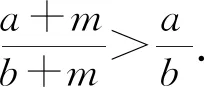
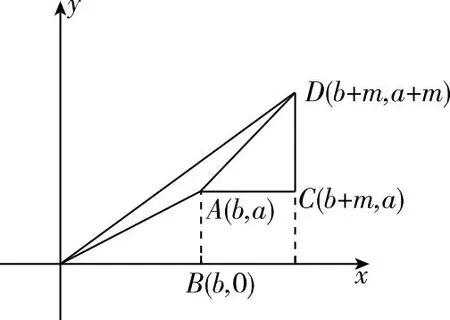
图2
“糖水不等式”还有更多的证明方法,在此不一一列举了.
4 “糖水不等式”的推广

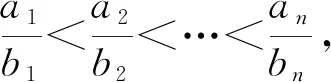

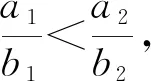
5 美妙的“糖水不等式”在各类题目中“大显身手”


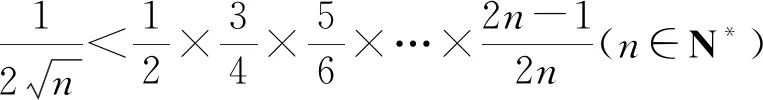
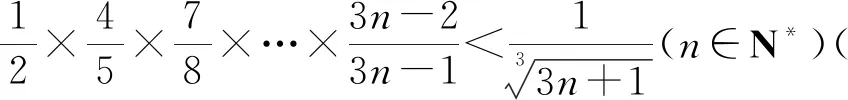
例2.(普通高中教科书(2019版A版)必修一·141页·13节选)比较大小:log34,log45.
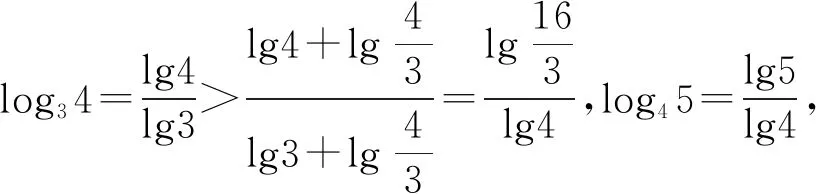
变式3.证明:logn(n+1)>log(n+1)(n+2)(n∈N*且n≥2).
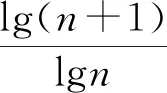
变式4.证明:当b>a>1,m>1时,logba 变式5.(2020·新课标Ⅲ卷·理12)已知55<84,134<85,设a=log53,b=log85,c=log138,则有 ( ) A.a C.b 变式6.(2022·新课标Ⅰ卷·12)已知9m=10,a=10m-11,b=8m-9,则 ( ) A.a>0>bB.a>b>0 C.b>a>0 D.b>0>a 例3.(2022·新高考Ⅰ卷·22节选)已知函数f(x)=ex-ax和g(x)=ax-lnx有相同的最小值,求a. 例4.(2015·湖北卷·理8)将离心率为e1的双曲线C1的实半轴长a和虚半轴长b(a≠b)同时增加m(m>0)个单位长度,得到离心率为e2的双曲线C2,则 ( ) A.对任意的a,b,e1>e2 B.当a>b时,e1>e2;当a C.对任意的a,b,e1 D.当a>b时,e1 我们学习中要以已有知识的经验为基础,以联系的眼光来看新题,发现题目结构与“糖水不等式”有相似的数量关系和结构属性,多观察、比较、分析、抽象概括、尝试灵活应用“糖水不等式”,在解题过程中感受“糖水不等式”的美妙,而不能死记硬背一些定理,所谓的二级结论,都是生搬硬套,从重视运算结果到过程和结果双重视,这才能有更强的学习数学参与感,在数学探究活动中善于发现类似的问题,善于总结类似的解题规律,同学们要从不同角度通过类比推理得到一般性结论,结合已有的学习经验,解决一类比较大小的问题. 从上述题型分类看出,利用“糖水不等式”可使原本复杂的解题思路变得清晰明了,找到解题通关的路径,启发大家在数学学习中,不仅要掌握知识,还要多研究知识的背景.教材的例题和习题都给我们提供很好的试题素材,多多钻研教材会有意想不到的收获,这样才能“从教材中学方法,应用教材做新题”!
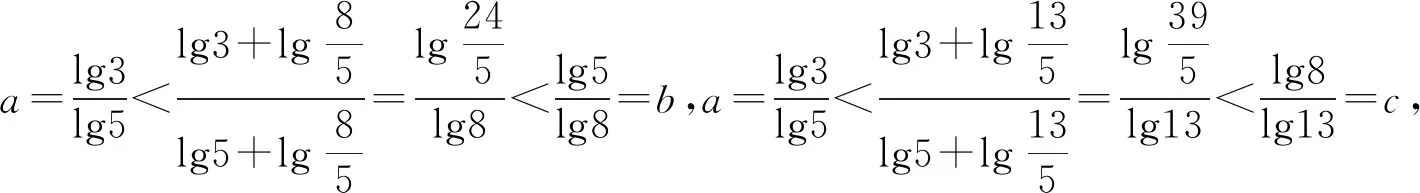
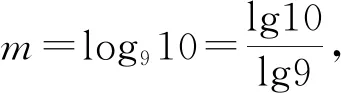
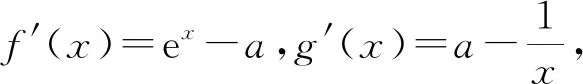
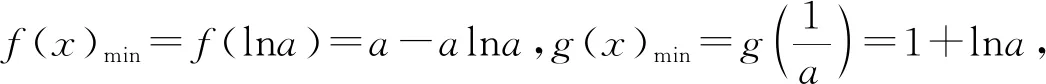
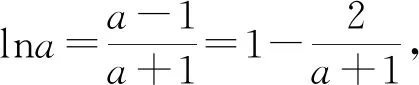
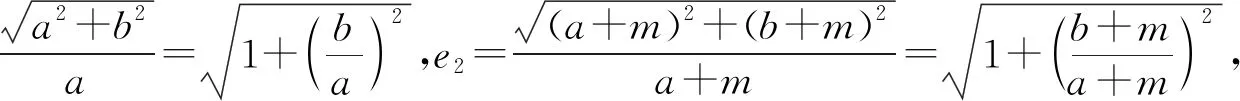
6 我们能从“糖水不等式”学到什么?

