复合材料纵横剪切模量的有限元计算与试验对比研究

王天琦 魏喜龙 王威力 李刚 魏程 单鹏宇 田忠恩

摘 要 层合板（±45°/90°/0°）是准各向同性层合板，其刚度在板面内各个方向上都相同。使用计算软件，编写程序代码，运用有限元的方法，划分有限元网格，计算了层合板（±45°/90°/0°）的纵横剪切模量［1］。将计算结果与复合材料纵横剪切模量试验结果进行对比，得到数值模拟和试验结果之间的误差为0.89 %，一致性很好，说明该计算方法可用于工程计算模拟。

关键词 复合材料层合板；准各向同性；有限元方法；纵横剪切模量

Research on Finite Element Method and Testing for

Determination Interlaminar Shear Modulus

of Composite Materials

WANG Tianqi，WEI Xilong，WANG Weili，LI Gang，

WEI Cheng，SHAN Pengyu，TIAN Zhongen

（Harbin FRP Institute Co.， Ltd.， Harbin 150028）

ABSTRACT Laminated plates （± 45°/90°/0°） are quasi isotropic laminates with the same stiffness in all directions within the plate plane. Using computational software， program code was written， and finite element method was used to divide the finite element mesh and calculate the longitudinal and transverse shear modulus of laminated plates （± 45°/90°/0°）［1］. The calculated results are compared with the transverse and longtitude shear modulus test results， it was found that the error between the numerical simulation and experimental results was 0.89%， indicating good consistency， indicating that this calculation method can be used for engineering calculation simulation.

KEYWORDS composite laminates；quasi-isotropic；finite element method；longitudinal and transverse shear modulus

通讯作者：王天琦，硕士研究生，助理工程师。研究方向为结构力学。E-mail：15145094822@163.com

1 引言

纤维复合材料由于其強度高、耐腐蚀等优点被广泛应用于航空航天和海洋等领域中。在复合材料的研发过程及工程应用中，经常要对不同的复合材料试件进行多种形式的性能试验，以获取所需的材料和结构性能参数。纤维增强复合材料的剪切性能是其基本性能之一，是复合材料设计中必须考虑的重要问题。许多结构铺层的设计、优化都是以剪切强度、模量数据作为依据。本文采用有限元数值模拟和试验对比的方法，对聚合物基复合材料层合板纵横剪切性能进行分析［2］。研究有限元数据模拟方法可在无试验条件下快速为复合材料结构件提供试验数据的依据。

2 准各向同性层合板的力学试验

2.1 复合材料层合板纵横剪切试件制备

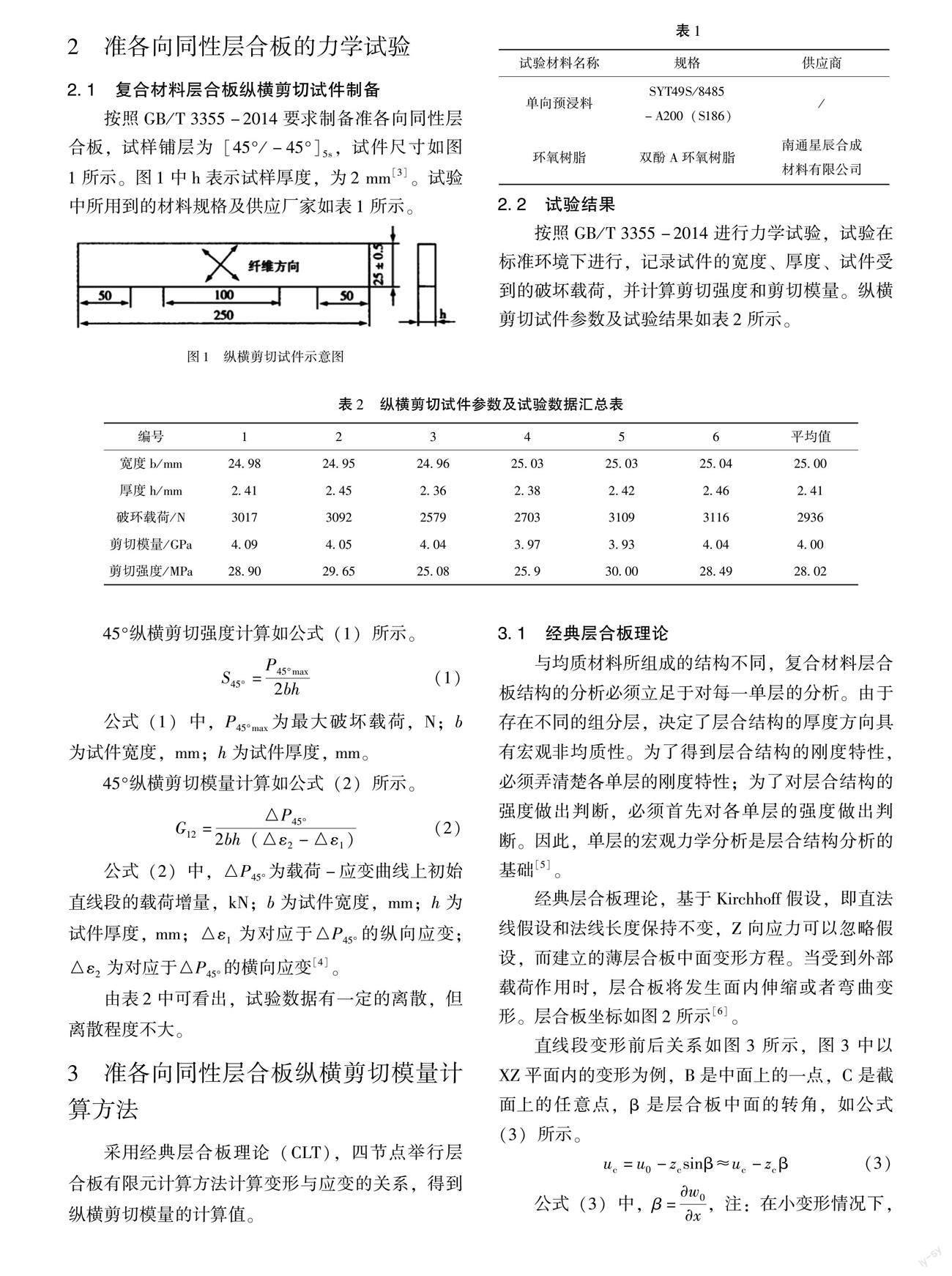
按照GB/T 3355-2014要求制备准各向同性层合板，试样铺层为［45°/-45°］5s，试件尺寸如图1所示。图1中h表示试样厚度，为2 mm［3］。试验中所用到的材料规格及供应厂家如表1所示。

2.2 试验结果

按照GB/T 3355-2014进行力学试验，试验在标准环境下进行，记录试件的宽度、厚度、试件受到的破坏载荷，并计算剪切强度和剪切模量。纵横剪切试件参数及试验结果如表2所示。

45°纵横剪切强度计算如公式（1）所示。

S45°=P45°max2bh（1）

公式（1）中，P45°max为最大破坏载荷，N；b为试件宽度，mm；h为试件厚度， mm。

45°纵横剪切模量计算如公式（2）所示。

G12=△P45°2bh（△ε2-△ε1）

（2）

公式（2）中，△P45°为载荷-应变曲线上初始直线段的载荷增量，kN；b为试件宽度，mm；h为试件厚度， mm；△ε1为对应于△P45°的纵向应变；△ε2为对应于△P45°的横向应变［4］。

根据上述试验，按照铺层［45°/-45°］5s制作碳纤维环氧树脂复合材料层合板，获得了碳纤维环氧树脂复合材料试件的基本力学参数，如表3所示。

由表2中可看出，试验数据有一定的离散，但离散程度不大。

3 准各向同性层合板纵横剪切模量计算方法

采用经典层合板理论（CLT），四节点举行层合板有限元计算方法计算变形与应变的关系，得到纵横剪切模量的计算值。

3.1 经典层合板理论

与均质材料所组成的结构不同，复合材料层合板结构的分析必须立足于对每一单层的分析。由于存在不同的组分层，决定了层合结构的厚度方向具有宏观非均质性。为了得到层合结构的刚度特性，必须弄清楚各单层的刚度特性；为了对层合结构的强度做出判断，必须首先对各单层的强度做出判断。因此，单层的宏观力学分析是层合结构分析的基础［5］。

经典层合板理论，基于Kirchhoff假设，即直法线假设和法线长度保持不变，Z向应力可以忽略假设，而建立的薄层合板中面变形方程。当受到外部载荷作用时，层合板将发生面内伸缩或者弯曲变形。层合板坐标如图2所示［6］。

直线段变形前后关系如图3所示，图3中以XZ平面内的变形为例，B是中面上的一点，C是截面上的任意点，β是层合板中面的转角，如公式（3）所示。

uc=u0-zcsinβ≈uc-zcβ

（3）

公式（3）中，β=w0x，注：在小变形情况下，才有β≈sinβ，根据上式，层合板上任意一点的位移u可以表示，如公式（4）所示。

u=u0-zw0x

（4）

同理在YZ平面内，也可以得到任意一点位移v的表达式如公式（5）所示。

v=v0-zw0y

（5）

另外，经典层合板理论中，任意一点的位移w与其中性面上的面外位移w0相等，如公式（6）所示。

w=w0（x，y）

（6）

公式（6）中，u、v、w分別为沿板厚范围内x，y，z方向的位移，中面上的点x，y，z方向的位移为u0、v0、w0，其中称为板的挠度［6］。

后续计算过程，依据上述理论进行。

3.2 变形与应变的关系

为了得到层合板的刚度矩阵和柔度矩阵，并且在有限元方法中运用，引入层合板的应力-应变关系。

为简化问题，对所研究的层合板作如下假设［7］。

（1）层合板各单层之间粘结良好，可作为一个整体结构板，并且粘结层很薄，其本身不发生形变，即各单层板之间变形连续。

（2）层合板虽由多层单层板叠合而成，但其总厚度仍符合假设，即厚度t与跨度L之比为（150～1100）＜tL＜18～110

（3）整个层合板是等厚度的。

在上述假设前提下，基于经典层合板理论中位移的表达式如公式（7）所示。

u（x，y，z）=u0（x，y）-zw0x

v（x，y，z）=v0（x，y）-zw0y

（7）

w（x，y，z）=w0（x，y）

引入几何方程，应变与位移的关系式如公式（8）所示。

εx=ux，εy=vy，εz=wz

γyz=wy+vz，γzx=uz+wx，γxy=yx+uy

（8）

将层合板的变形带入上式可得如公式（9）所示。

εx=ux=u0x-z2w0x2=εx0+zkx

εy=vy=v0y-z2w0y2=εy0+zky

γxy=uy+vx=u0y+v0x-2z2w0xy=γxy0+zkxy（9）

式中，kx，ky为中面的弯曲挠曲率，即曲率半径的倒数，kxy为中面的扭曲率，εx0、εy0、γxy0为中面应变［8］。

将总应变整合后形式如下，其中第一部分代表的是面内的应变，第二部分代表的是弯曲引起的应变，

如公式（10）所示［9］。

{ε}={εo}+z{k}

{εo}u0x

v0y

u0y+v0x

（10）

{k}=

2wx2

2wy2

-22wxy

将公式（8）代入单层板应力-应变关系式，可以得到层合板中第k层的应力-应变关系式［10］：

σxσyσz=Q11 Q12 Q16

Q12 Q22 Q26

Q11 Q26 Q66

εxoεyoγxyo+zkxkyzkxy

（11）

式（11）中Q为刚度矩阵，由公式（9）可知，层合板应变由中缅应变和弯曲应变两部分组成，沿厚度线性分布；而应力除与应变有关外，还与各单层刚度特性有关，若各层刚度不相同，则各层应力不连续分布，但在每一层内是线性分布的［11］。

3.3 四节点矩形层合板有限元计算纵横剪切模量

有限元法的基本理念是假设将一个连续体分割成数目有限的小体（单元），彼此间只在数目有限的指定点（节点）处互相连结，组成一个单元的集合体以代替原来的连续体，再在节点上引进等效力以代替实际作用于单元上的外力。因此，可以选择一个简单的函数来近似地表示位移分量的分布规律，建立位移和节点力之间的关系，把有无限个自由度的连续体理想化为有限个自由度的单元集合体，使问题简化为适合于数值解法的结构型问题［12］。

基于复合材料层合板理论，结合3.1及3.2中的理论计算结果，建立并划分的层合板有限元网格如图4所示，在节点1，2，3上施加了边界条件-即将所有自由度固定。

图4 层合板试件有限元数值模拟图

在节点13和15上，沿x轴施加25 N的力，在节点14上，沿x轴施加50 N的力，施加载荷为100 N。层合板试件厚度如公式（12）所示。

H=n·δ=10·0.24=2.4 mm （12）

式中，δ为单层厚度0.24 mm。

将节点8和节点11之间沿X轴的相对伸长量定义为ε1，沿Y轴的相对伸长量定义为ε2。则沿X轴的剪切强度和相对伸长量如公式（13）～（16）所示。

τ=F2bH=0.83333 MPa（13）

ε1=u（11）-u（8）a=0.0001274（14）

ε2=u（11）-u（8）a=0.000018（15）

γ=ε1-ε2（16）

即剪切模量如公式（17）所示。

G12′=△τ△γ=4035.61MPa （17）

试验结果与有限元数值模拟结果之间的误差如公式（18）所示。

ψ=G12′-G12G12=0.89%

（18）

数值模拟中用到的参数如表3所示。

由表2中数据可知，试验结果与数值模拟得出的层合板剪切模量相差不大，误差仅在1%以内，存在误差的主要原因是模拟使用的摩擦参数与试验实际情况有差别，并且试验使用的板料厚度也存在一定的偏差，这些因素的综合影响导致了有限元模拟与试验值之间的偏差［13］。

4 结语

基于经典层合板理论，运用计算软件并使用有限元分析方法对复合材料层合板的纵横剪切试验进行数值模拟，提出了一个含有前后处理的完整的四节点有限元程序算法，该程序算法可以为模拟层合板的拉伸、压缩等力学性能提供计算基础［14］。本文研究分析得到了层合板的纵横剪切模量，根据数值模拟后的数据显示，有限元方法在一定程度上可以得到比较准确的预测复合材料层合板的力学性能，能够指导复合材料层合板铺层结构［15］，有限元数据和试验数据之间的误差在1%左右，使用有限元数值模拟方法计算剪切模量的方法是可行的，可以满足工程需要。

参 考 文 献

［1］杨涵，周仕刚，薛元德.（±45°/90°/0°）s准各向同性层合板的拉伸强度［J］.纤维复合材料， 2010（4）：5.DOI：10.3969/j.issn.1003-6423.2010.04.001.

［2］鲍宏琛，刘广彦.准各向同性纤维增强复合材料层合板的开孔拉伸破坏模拟［J］.复合材料学报， 2016， 33（5）：7.DOI：10.13801/j.cnki.fhclxb.20160112.005.

［3］刘宝良，夏军.基于Mindlin理论的复合材料层合板的有限元分析［J］.黑龙江科技大学学报， 2004， 14（3）：171-173.DOI：10.3969/j.issn.1671-0118.2004.03.010.

［4］朝鲁，张鸿庆，唐立民.一个计算微分方程（组）对称群的Mathematica程序包及其应用［J］.计算物理， 1997， 14（003）：375-379.DOI：10.1007/BF02947208.

［5］邵明.有限元法在复合材料层合板力学性能中的应用研究［D］.浙江大学，2013.

［6］李真，陈秀华，汪海.基于重合网格法的含孔复合材料层合板有限元分析［C］//第17届全国复合材料学术会议.中国力学学会;中国宇航学会;中国航空学会;中国复合材料学会， 2012. DOI：ConferenceArticle/5af1b392c095d71bc8cb4150.

［7］李斯华李良伟.复合材料层合板的层间应力有限元分析［J］.四川建材， 2013， 039（001）：63，66.

［8］Жилин П.А. Векторы и тензоры второго ранга в трехмерном пространстве. СПб.： Нестор， 2001. 276 с.

［9］Жилин П.А. Рациональная механика сплошных сред： учеб. пособие. СПб.： Изд-во Политехн. ун-та， 2012. 584 с.

［10］Сорокин Ф.Д. Прямое тензорное представление уравнений больших перемещений гибкого стержня с использованием вектора конечного поворота // Известия РАН. Механика твердого тела. 1994. № 1. C. 164-168.

［11］Кувыркин Г Н， Головин Н Н， Петрикевич Б Б， et al. Разработка теоретических основ и методов оценки несущей способности и прочностной надежности （риска разрушения） термонапряженных элементов конструкций из композитных материалов на основе углерода［R］. Российский фонд фундаментальных исследований， 1994.

［12］Демидов А С， Хомовский Я Н. Особенности расчёта и выбор критериев напряженно-деформированного состояния для тонкостенных конструктивных элементов из углерод-углеродных композитных материалов［J］. Sciences of Europe， 2016 （9-4 （9））： 80-84.

［13］王言磊，郝慶多，欧进萍.复合材料层合板面内剪切实验方法的评价［J］.玻璃钢/复合材料， 2007（03）：6-8.DOI：10.3969/j.issn.1003-0999.2007.03.002.

［14］张纪奎，郦正能，关志东，等.复合材料层合板固化压实过程有限元数值模拟及影响因素分析［J］.复合材料学报，2007， 24（2）：6.DOI：10.3321/j.issn：1000-3851.2007.02.022.

［15］许良梁，矫桂琼，卢智先，等.含分层复合材料层合板剪切屈曲的实验研究［J］.机械强度，2007， 29（4）：5.DOI：10.3321/j.issn：1001-9669.2007.04.011.