几个三角形不等式的再探究
2024-04-15 06:39湖南省长沙市望城区中小学教师发展中心410200刘先明
中学数学研究(江西) 2024年4期
湖南省长沙市望城区中小学教师发展中心 (410200) 刘先明
设ΔABC的三边长、三边对应的高、对应的旁切圆半径、外接圆半径、内切圆半径、半周长分别为a,b,c,ha,hb,hc,ra,rb,rc,R,r,s,用∑、∏表示循环求和、循环求积.文[1] 提供了加拿大数学杂志Crux Mathematicorum 4596题:

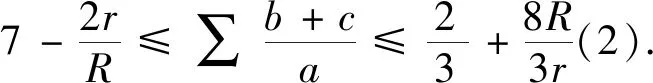
文[2] 提供了加拿大数学杂志Crux Mathematicorum 3450题:
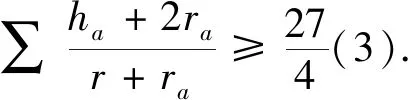
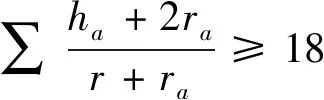

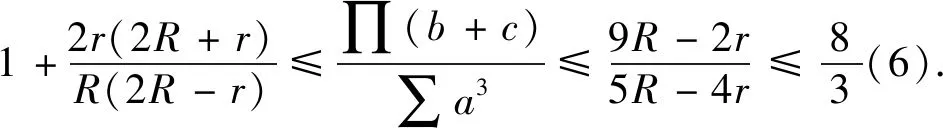
本文获得(1)、(2)、(5)、(6)式的加强.为证明相应的结论,先给出如下已知的结果.
引理1 (文[4])在ΔABC中,有∑a=2s,∑bc=s2+4Rr+r2,abc=4Rrs,∑a3=2s(s2-6Rr-3r2),∏(b+c)=2s(s2+2Rr+r2).
引理2 (Gerretsen不等式)在ΔABC中,有16Rr-5r2≤s2≤4R2+4Rr+3r2,当且仅当ΔABC为正三角形时取等号.
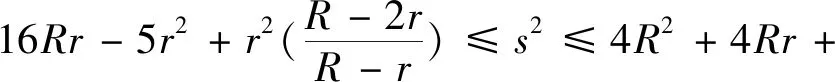
1.(1)式的加强及下确界

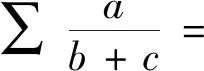
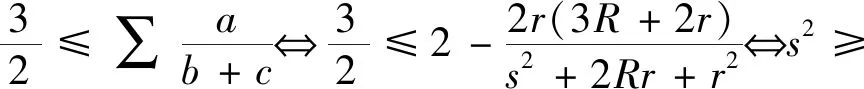
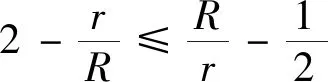
从而结论1是下述Nesbitt不等式的特例.

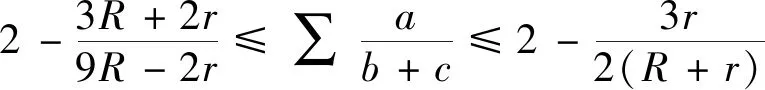
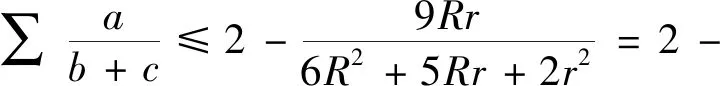
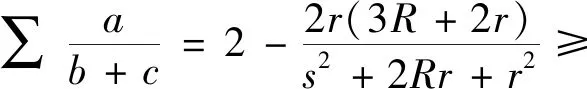
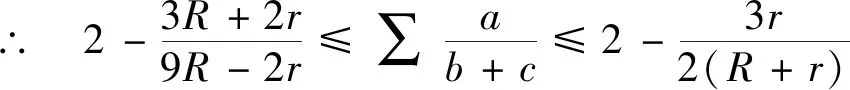
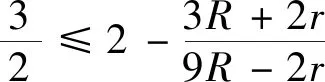
2.(2)式的加强
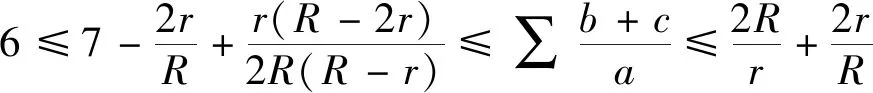
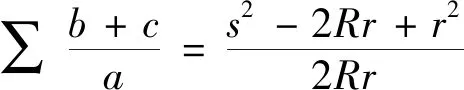
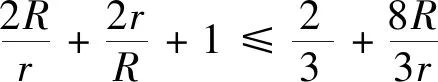
同时,获得欧拉不等式R≥2r的加强:
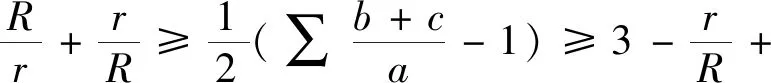
3.(5)式的加强
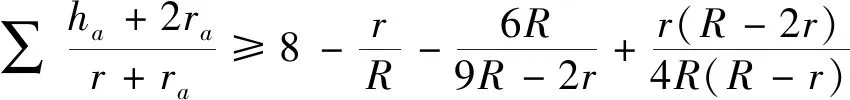
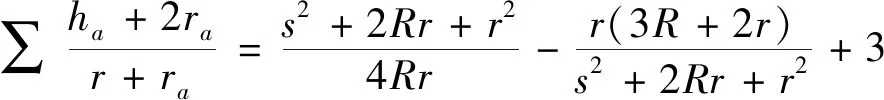
4.(6)式的加强
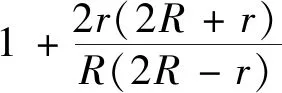

猜你喜欢
河北理科教学研究(2021年2期)2021-08-18
中等数学(2021年1期)2021-07-23
中等数学(2021年2期)2021-07-22
中等数学(2020年9期)2020-11-26
音乐天地(音乐创作版)(2019年10期)2020-01-06
中学数学教学(2019年3期)2019-06-21
中等数学(2018年8期)2018-11-10
中等数学(2018年7期)2018-11-10
中学数学杂志(高中版)(2018年1期)2018-01-27
音乐天地(音乐创作版)(2016年1期)2016-04-03

