两个三角基本不等式及推论的应用*

四川省成都七中数学组 (610000) 夏 雪

四川省成都西藏中学 (610000) 汪 洋

三角函数与导数综合问题在近期试题中非常常见.三角函数具有的单调性、有界性、求导特征均为导数的研究带来活力.本文对涉及三角函数的导数的几个不等式及其应用展开讨论,以展示这类不等式的重要应用.

一、两个三角基本不等式

不等式1 当x>0时,sinxx.

注:该不等式可统一成|sinx|≤|x|(当且仅当x=0时取等).

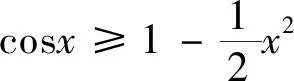
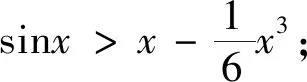
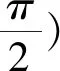
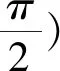
二、三角基本不等式的应用

(1)当a=0时,求b的取值范围;

(2)求证:a2+b2>e.

解:(1)易求得b∈[2e,+∞).

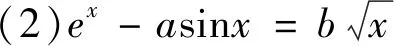
点评:此题为2022年天津卷高考导数压轴题,难度较大.若能从构造a2+b2入手,借助柯西不等式及前面所述三角基本不等式,可以找到该题的简洁解答.

例2 已知函数f(x)=ae-x+sinx-x.

(1)若f(x)在(0,2π)单调递减,求实数a的取值范围;(2)证明当a∈Z时,f(x)至多一个零点.

解:(1)f′(x)=-ae-x+cosx-1,令f′(x)≤0,则-a≤ex(1-cosx)对x∈(0,2π)恒成立,但ex(1-cosx)>0,且当x→0时ex(1-cosx)→0,条件等价于-a≤0⟺a≥0.故所求范围是a≥0.

(2)令f(x)=0,则a=ex(x-sinx)=g(x),则g′(x)=ex(x-sinx+1-cosx).当x≥0时,g′(x)≥0,故g(x)在[0,+∞)单调递增,值域[0,+∞).当x<0时,由x-1,即证ex(x-sinx)>-1⟺e-x+x-sinx>0.事实上,e-x+x-sinx>-x+1+x-sinx=1-sinx≥0,于是当x<0时g(x)∈(-1,0).

综上所述,对于a∈Z,当a≥0时,f(x)恰有一个零点;当a<0时f(x)无零点.

点评:此题的巧妙之处在于利用零点的等价转化构造函数g(x).而函数g(x)的研究借力三角基本不等式1,注意到a∈Z,此命题易证.

例3 若关于x的方程mxsinx+x=ex-1(0≤x≤π)有两个不等实数根,求实数m的取值范围.

点评:解法一采用先分离及三角基本不等式的放缩,寻找不等式成立的必要条件.再证充分性;解法二采用分象限讨论,结合零点存在定理,这是处理三角函数与导数问题相结合问题的常见方法.

例4 已知函数f(x)=asinx+sin2x,a∈R.

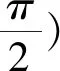
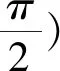
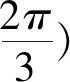
点评:此题首先寻找不等式成立的必要条件.再证充分性.充分性的证明过程借助了三角基本不等式二的推论1,使得证明过程简洁明了.