基于多重降质复合信道的UWOC 系统误码率性能研究

张建磊，张鹏伟，朱云周，田雨欣，李婕妤，杨祎，贺锋涛

（1 西安邮电大学 电子工程学院， 西安 710072） （2 中国科学院西安光学精密机械研究所，西安 710119）

0 引言

水下无线光通信（Underwater Wireless Optical Communication， UWOC）系统可在水下环境中实现高效数据传输。相比传统水下通信方式受限于声波传输的低速和干扰的局限，水下无线光通信系统充分利用了光在水中的传播特性，为水下通信领域带来了新的突破和可能性。该系统工作于400～550 nm 波段的蓝/绿光频谱范围内，相较于声学系统，具备高数据速率、低延迟、高传输安全性和低能耗等优点［1-3］。尽管具有显著的优势，光在水下的传播也受到多重降质效应的影响，包括吸收、散射、气泡和湍流，限制了水下无线光通信系统的可行通信范围［4-5］。因此，研究水下无线光通信在这种复杂环境下的应用仍然具有挑战性。

文献［6-8］对UWOC 通道中的吸收和散射效应进行了广泛的研究，但忽略了水下湍流对系统的影响。水下湍流衰落是UWOC 系统中不可忽视的问题，由水下环境中的湍流运动引起。湍流衰落会使光信号在传输过程中发生随机变化，影响接收端的光功率稳定性。文献［9-11］修改了现有的大气湍流对数正态分布信道模型，以描述水下环境中的辐照度波动。然而，大气的温度折射率变化谱和水下的温盐折射率谱存在显著差异，使得对数正态分布不适合模拟水下湍流引起的辐照度波动。为此，文献［12］提出了混合指数-对数正态模型来描述UWOC 通道中的辐照度波动。然而，指数对数正态分布在UWOC 信道中的应用使得重要性能指标（如中断概率和平均误码率）很难获得封闭形式和易于使用的表达式。文献［13］中研究了考虑湍流、吸收和散射效应的水下无线光通信链路的性能。其中，弱湍流通道采用对数正态分布进行建模，而中强湍流通道采用Gamma-Gamma 分布进行建模。然而，该研究忽略了气泡对系统性能的影响。在海洋中，气泡是由波浪破碎产生的［14］，已经发现气泡可以显著增强光信号的散射作用［15］。水下气泡的存在及其对光信号传播的影响已得到很好的证实［16-18］。因此，文献［19］提出了混合指数广义伽玛（Exponential-Generalized Gamma， EGG）分布模型，有效且统计地描述了大气泡和温度诱导的从弱到强湍流条件下使用淡水和咸水的辐照度波动。然而，该模型并没有考虑吸收和散射效应以及微气泡对系统通信链路性能的影响。

本文基于米（Mie）散射理论计算水下微气泡群的光散射特性，并结合EGG 湍流分布模型，推导了综合考虑吸收、散射、气泡和湍流的复合信道在通断键控（On-Off Keying，OOK）调制方式下误码率的封闭表达式，并仿真分析了闪烁指数、单位体积内气泡数量、不同海水水质对误码率的影响。

1 基本理论

1.1 米散射模型

1.1.1 单个气泡的米散射模型

Mie 散射模型是计算水中均匀球形微气泡光散射特性的有效方法。根据Mie 散射［20］，当一束光强为I0、波长为λ的自然光沿着z轴正方向平行辐射至气泡时（气泡的相对折射率为m，气泡位于O处），气泡会向空间各个方向散射光。散射后的光强为I，散射角为θ，散射面与入射光振动方向的夹角记为φ，散射体到测量点的距离记为R，图1 为单气泡的光散射模型。

图1 单气泡的光散射模型Fig. 1 Modeling light scattering from a single bubble

经过散射后的光强I可以表示为

式中，i1=|S1(m，θ，x)|2，i2=|S2(m，θ，x)|2分别表示散射强度函数；S1是散射光复振幅函数的垂直分量，S2是散射光复振幅函数的平行分量；m为气泡与海水的相对折射率；x=2πrn0/λ为粒子的尺度因子，r为气泡的半径，n0为海水的折射率。

根据Mie 散射系数可以计算出气泡的散射振幅S1和S2为

式中，an和bn为Mie 散射系数；πn和τn为散射角函数，是缔合勒让德函数的函数，即

它们满足递推关系

其初始值为π0=0，π1=1。

an和bn可以通过Mie 理论计算，即

式中，ψn(z)和ξn(z)分别为黎卡蒂贝塞尔函数和第二类黎卡蒂汉克尔函数，满足递推关系

初始值分别为ψ-1=cosz，ψ0=sinz，ξ1=exp(iz)和ξ0=-i exp(iz)。

根据Mie 散射系数an和bn可以进一步计算出气泡的光学效率因子。光学效率因子包括散射效率因子Qsca、消光效率因子Qext和吸收效率因子Qabs，其计算公式为

为了提高计算效率，使用Wiscombe 给出的经验公式［21］确定上限N的值，即

值得注意的是，由于气泡对光的吸收作用可以忽略，因此气泡的散射效率因子与消光效率因子相等。

结合Mie 散射系数an和bn以及散射效率因子Qsca，可以计算出气泡的散射强度函数和散射相函数。散射强度函数描述了不同方向散射光强度的大小，而散射相函数则为散射强度函数的归一化形式，定义为光在某个给定方向单位立体角中的散射能量与在所有方向上平均的单位立体角中的散射能量之比。

单气泡散射光的散射强度函数为

气泡的体散射相函数P(θ)的数学表达式为

1.1.2 微气泡群的米散射模型

气泡群的Mie 散射计算模型主要包括气泡群的体散射函数和散射相函数的计算模型。

体散射函数［22］（Volume Scattering Function，VSF）β(θ)是水体的一个重要光学特性参数，用于描述光在水体中受某一散射体散射后散射光的角度分布。在辐射学上定义为：在某一方向ψ单位散射体积V、单位立体角内散射辐射强度E与入射体积上的辐射照度之比，单位为m-1sr-1，即

对于气泡群而言，其VSF 为

式中，Qβ(θ，r)为粒径为r的粒子在方向θ上每单位立体角的散射效率，可以通过Mie 散射函数进行定义；rmax、rmin为粒子的最大和最小半径；n(r)是气泡尺寸分布函数，表示为单位体积内所含半径为r的粒子个数，其与尺度分布概率密度函数p(r)满足

式中，N0为单位体积内气泡的数量，其数量级一般可达106～109［23］，单位为个/m3；p(r)为气泡尺寸的概率密度函数。常用的分布为Junge 谱分布［24-25］，其表达式为

当入射光为自然光时，体散射函数为

由于不考虑气泡的吸收作用，因此气泡群的衰减系数和散射系数相同。气泡群的散射系数为

气泡群的散射相函数为归一化的体散射相函数，计算公式为

通过式（18）可知，气泡群的散射相函数与气泡群的密度无关。当气泡的相对折射率为0.75，入射光波长λ=532 nm 时，利用Junge 谱对30～300 μm 的气泡尺寸每间隔10 μm 进行抽样并根据式（18）进行计算，可得到不同半径尺寸的单气泡的角散射效率，如图2 所示。通过对各角度的散射效率求平均，即可得到气泡群的平均散射相函数如图3 所示。

图2 30～300 μm 范围内不同半径尺寸单个气泡的角散射效率Fig. 2 Angular scattering efficiency of single bubbles with different radius sizes in the range of 30～300 μm

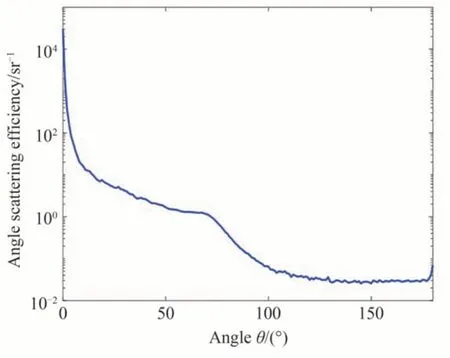
图3 气泡群的平均散射相函数Fig. 3 Average scattering phase function of bubble populations

气泡群的散射相函数难以使用数学公式来准确表达。通过对气泡群散射相函数分布特性分析可知，气泡群的散射大多发生在0°～20°的散射，其散射光强存在前向散射远大于后向散射的特点，并且气泡群在临界角82.7°附近存在突变，该突变可以用来区别水中气泡散射与粒子散射。由于大气和水的折射率不同，当复合信道不含气泡仅有粒子散射效应时，不发生跨界面的散射，相应的散射相函数也不会出现该部分的突变，相反考虑气泡的散射效应时则会发生该突变。

1.2 复合信道的光学特性

现有的信道仿真模型大多仅考虑粒子的吸收与散射，为了综合考虑粒子的吸收散射、气泡和湍流等多重降质效应对UWOC 系统信号传输特性的影响，对水下复合信道进行建模。图4 为所建立的复合信道模型，发射端为具有一定的数量、位置和初始方向的光子的集合，接收端可以设置一定的位置、形状和接收角等。光信号在传输过程中会受到信道中多重降质因素所带来的衰减效应，从而造成能量损耗或路径偏离。

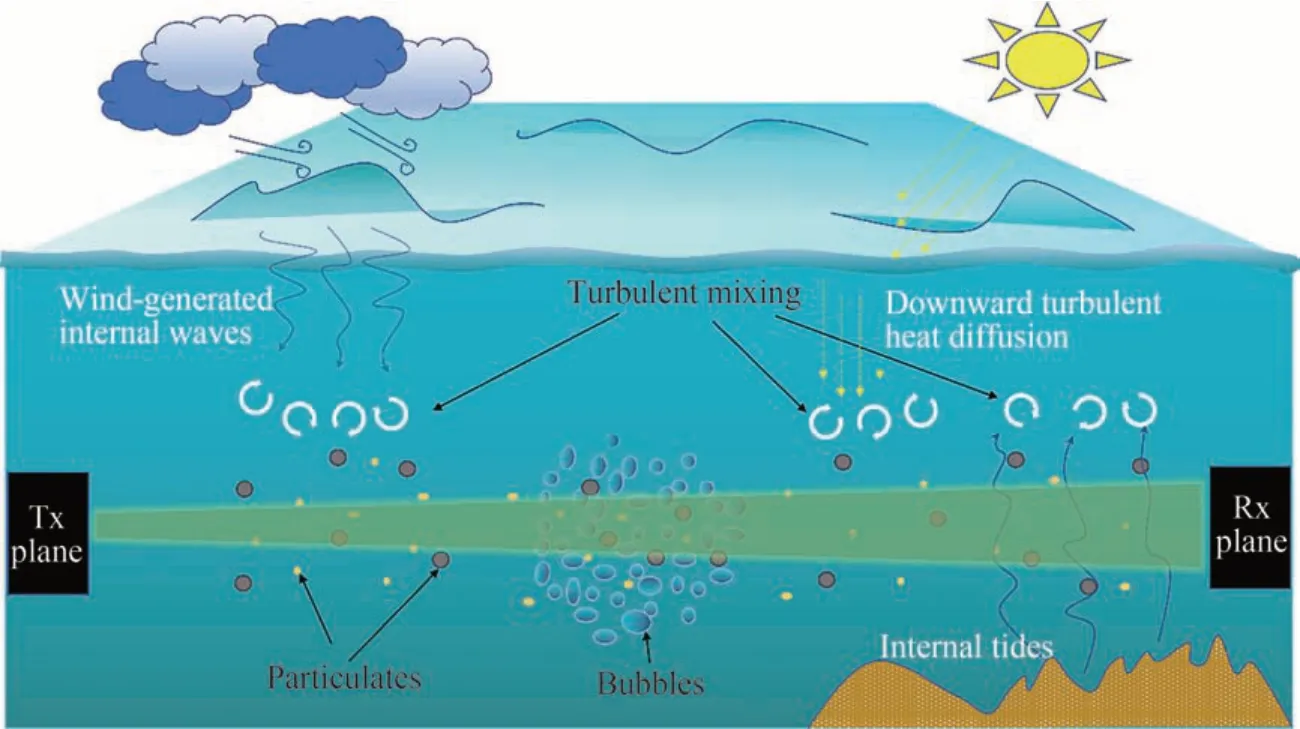
图4 多重降质复合信道链路示意图Fig. 4 Schematic diagram of multiple degraded mass composite channel links

与自由空间光通信不同，光束在海水中传播时，海水中的杂质、颗粒物会与每个光子发生吸收、散射作用，降低光强的平均辐照度。由吸收和散射效应引起的总衰减可用衰减系数c(λ)描述为［26］

式中，a(λ)、b(λ)分别表示海水的吸收和散射系数。

复合信道的吸收系数可以建模为各部分的吸收系数之和［27］，即

式中，aw(λ)、ap(λ)、as(λ)和ay(λ)分别为纯海水、叶绿素、悬浮泥沙以及黄色物质的吸收系数。

由于气泡对光的吸收作用极弱，所以不考虑气泡对吸收作用所作的贡献。同理，复合信道的散射系数可表示为

式中，bw(λ)、bp(λ)、bs(λ)、bbub(λ)分别表示纯海水、叶绿素、悬浮颗粒以及气泡的散射系数。

由于各成分对总吸收散射的贡献难以分别计算，当入射光波长为532 nm 时已有研究人员通过实际测量，划分出不同水质下的吸收、散射系数和衰减系数，如表1 所示。微气泡群的散射系数由式（17）计算。

表1 不同水质下的衰减系数［28］Table 1 Attenuation coefficients for different water qualities ［28］

根据Beer-Lambert 定律，可将光信号在海水中受到的衰减用其一般指数模型表示为

式中，L表示海水中透射光束的传输距离。本文复合信道在原有的粒子散射基础上引入气泡这一参数概念，然后结合粒子与气泡衰减得到了水下复合信道衰减损耗hl，即

式中，散射系数bbub(λ)由式（17）计算。

1.3 系统模型

海水信道是一种复杂时变信道，光信号在海水信道传输时，杂质分子的吸收、散射效应和光源发散角引起光束扩展都会使光信号的功率衰减。而海洋湍流引起接收信号幅度随机波动的过程可近似为将海洋湍流作为乘性噪声对信号进行调制，系统噪声近似成加性高斯白噪声。建立综合考虑海洋湍流和水下信号衰减的水下无线光复合信道模型，经该信道传输后，接收端光信号可以表示为

式中，h代表信道状态，Ii(t)为发射端发射的光信号，Ni为系统噪声。综合考虑吸收散射、微气泡及湍流等多重降质效应时，复合信道状态可以表示为

式中，hl(λ，L)为水下吸收散射和微气泡所引起的衰减，ht(t)为水下湍流引起的衰减。

1.4 湍流信道模型

湍流效应引起的信号衰落严重影响水下无线光通信性能，信道模型的选择对系统评估至关重要。研究者已提出了多种光强分布统计模型来模拟水下湍流造成的衰落现象，通常使用的有对数正态分布［29］、Gamma-Gamma 分布［30］、威布尔分布［31］、广义伽马分布［32］以及混合指数广义伽马分布［33］等。

为了更好地描述海洋湍流引起的光强辐照度变化和分析光强闪烁效应，使用EGG 分布模型表征不同海洋湍流强度下由大气泡和温度梯度引起的光强辐照度波动，EGG 分布的概率密度函数（Probability Density Function， PDF）表示［33］为

式中，ω为分布的混合权值，满足0 ＜ω＜1；ζ为指数分布的相关参数；a、b和c为广义伽马分布的参数；f(I；ζ)和g(I；[a，b，c])分别表示指数分布函数和广义伽马分布函数，即

式中，Γ(·)为伽马函数。EGG 分布的PDF 可进一步表示为

衰落信道函数可表示为

式中，E[·]表示期望值。

将式（26）代入EGG 分布的n阶矩可得

由式（32）和（29）可得EGG 分布下的闪烁指数表达式为

海水湍流导致信号光强闪烁，在进行通信系统仿真时，将海洋湍流信道等效为湍流乘性噪声引入到发射信号中，对信号进行调制。

1.5 系统平均误码率的推导

系统瞬时信噪比可以表示为

式中，Ps为接收端电信号功率，Ni为加性高斯白噪声功率。

式中，η为光电转换系数，I为信号接收光强，j是检测技术类型的参数（即外差检测：j=1，IM/DD：j=2），RL为等效负载电阻。

系统的平均电信噪比μr可表示为

平均电信噪比μr与平均信噪比γˉ的关系为

使用OOK 调制方案的UWOC 系统的误码率表示为

式中，fh(h)为波动光强度的概率密度函数。

考虑吸收散射、气泡和湍流等多重降质效应的条件PDF 表示为

考虑吸收散射和气泡对信道的影响，可以将EGG 模型PDF 表示为

将式（40）代入式（38），则使用OOK 调制下的系统误码率为

根据Meijer-G 函数指数函数性质［34］，exp( ·)可以表示为

erfc( ·)函数可以用文献［35］式（8.4.14.2）展开为

用erfc( ·)函数和exp( ·)函数展开得到复合信道下UWOC 系统的平均误码率表达式为

2 仿真分析

基于理论分析得到的多重降质复合信道链路的误码率表达式进行仿真分析，仿真参数采用波长为523 nm 的绿光，设定发射孔径半径为10 mm，接收孔径半径为20 mm，光源发散半角为0.5 mrad，发射功率为1 W，等效负载电阻为50 Ω，噪声功率为0.5 mW。

在清澈海水水质中，链路距离为25 m，采用OOK 调制通过复合信道传输。研究了不同闪烁指数条件下平均误码率随接收端信噪比的变化曲线，结果如图5 所示。可以观察到，当系统平均误码率水平达到10-3时，在闪烁指数=0.148 4 和=0.476 9 的湍流条件下所需的最小接收端信噪比分别为17.3 dB 和23.7 dB。随着湍流强度的增加，实现系统特定平均误码率所需的最小接收端信噪比逐渐增加。在相同信噪比条件下，湍流强度的增加对系统性能有较大影响，导致误码率性能逐步恶化。

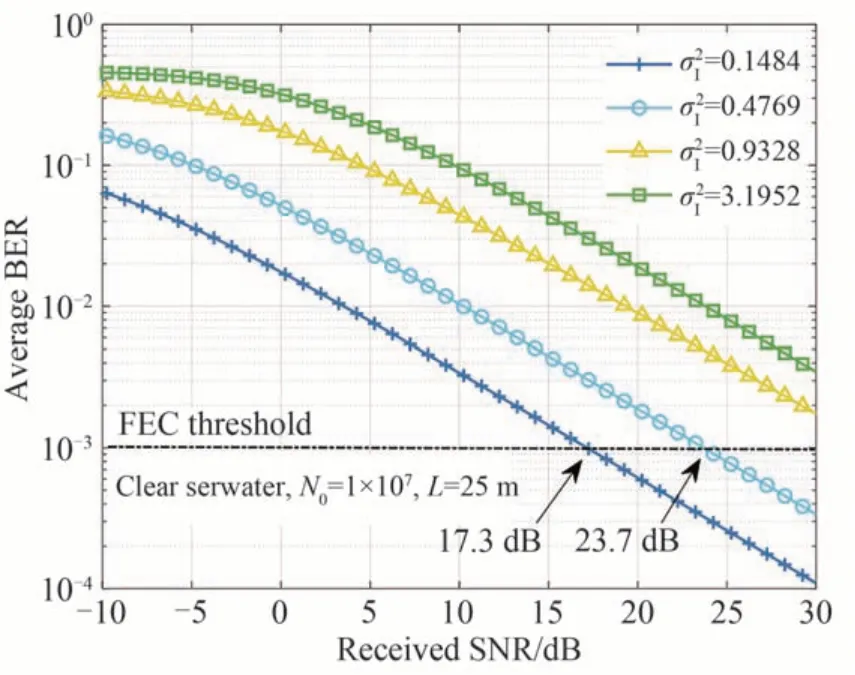
图5 不同湍流强度下UWOC 系统的平均误码率与信噪比的关系Fig. 5 Average BER versus signal-to-noise ratio for UWOC systems with different turbulence intensities

图6 展示了在清澈海水环境中，基于OOK 调制的UWOC 系统经过复合信道后，随着链路距离变化而产生的误码率曲线。该曲线考虑了不同气泡数量在闪烁指数=0.319 2 的强湍流条件下对系统性能的影响。从图中可以观察到，随着信道中气泡数量的增加，系统的误码率逐步增大。保持链路距离在20 m 时，单位体积内气泡数量为3×106，对应系统平均误码率为4.57×10-4。而单位体积内气泡数量从3×106增加到9×106和9×107时系统的平均误码率分别为5.76×10-4、1.19×10-2。这是因为气泡的存在会引起光信号的散射衰减效应，导致光的散射现象发生，光线在气泡表面发生反射和折射，使得光信号的传播路径变得复杂。这种散射现象导致接收端接收到的光功率降低，从而增加了系统的误码率。

图6 不同气泡数量下UWOC 系统的平均误码率与链路距离的关系Fig. 6 Average BER versus link distance for UWOC systems with different number of bubbles

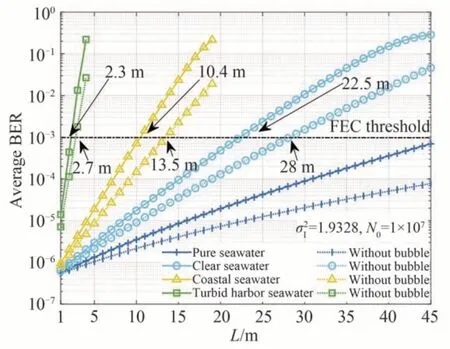
图7 不同水质下UWOC 系统的平均误码率与链路距离的关系Fig. 7 Average BER versus link distance for UWOC systems with different water quality

图8 展示了在清澈海水水质条件下，气泡数量为1×107时，UWOC 系统采用OOK 调制信号经过复合信道后，在不同湍流强度下系统平均误码率随链路距离的变化关系。研究结果显示，闪烁指数为=0.148 4、=0.476 9、=1.932 8 和=3.159 2 的湍流条件下，链路距离最远分别为31.8 m、28.0 m、22.5 m 和20.1 m 方可保证实现系统误码率低于10-3的可靠通信质量。由图8 可知，随着链路距离增加，四种湍流强度下系统的平均误码率都呈现线性劣化趋势。这一趋势的出现是因为在UWOC 系统中，光信号在水中传播时会受到光强衰减的影响。随着链路距离的增加，光线经过的路径长度增加，导致光强度逐渐减弱，光强衰减会使接收端的信号强度降低，进而增加误码率。

图8 不同湍流强度下UWOC 系统的平均误码率与链路距离的关系Fig. 8 Average BER versus link distance for UWOC systems with different turbulence intensities

3 结论

本文基于Mie 散射理论，计算了海洋微气泡群的光散射特性，包括体散射函数、散射系数和散射相函数。综合考虑吸收散射、气泡衰减信道和EGG 分布湍流信道，建立了复合信道模型，并将复合信道对信号的衰减与湍流噪声等效到信号上，推导了该复合信道在OOK 调制方式下误码率的封闭表达式。基于理论表达式，评估了不同海水水质、湍流强度、气泡数量以及链路距离对系统误码率性能的影响。研究结果表明，随着链路距离的增加，误码率呈线性劣化趋势。在四类水质中，港口海水由于其高浊度和多悬浮颗粒物难以满足系统正常通信。同时，气泡数量和链路距离的增加也导致系统的误码率严重劣化。为了使平均误码率保持在几十米的可接受实际范围内，建议采用空间或多径分集技术、相关分集和多跳传输技术，以及孔径平均减缓技术来进一步提高UWOC 系统的性能。