基于夹持粘贴式的光纤光栅传感器力热耦合测试
李鑫,黄薏静,于纪成,徐赵洁,马冠军
(北方工业大学 机械与材料工程学院, 北京 100144)
0 引言
光纤布拉格光栅(Fiber Bragg Grating, FBG)传感器具有精度高、稳定性好、易成传感网络等特征,且由于其材料的非金属性,具有绝缘性、不受电磁干扰以及耐腐蚀等优势,在航空航天、建筑桥梁、石油勘探等方面具有很大的应用前景[1-5]。在高温环境下的应变测试方面,传统高温应变传感器存在电阻应变片的引线不绝缘、易受电磁影响,且复用性差等不足[6];高温引伸计发展不成熟,产品昂贵,对使用的空间求较高,较依赖进口产品[7]。而光纤光栅传感器可实现多场耦合参数的测量,更适合于高温、高电磁的极端环境。
HILL K O 等[8]于1978 年研制出光纤光栅,MOREY G 和MELTZ WW 等[9]首次发现光纤光栅的中心波长与温度-应变变化呈现线性关系,国内外研究者由此开展了针对光纤光栅温度-应变交叉敏感方面的研究。田琴等[10]研制一种双热重生布拉格光栅(Regenerated Fiber Bragg Grating, RFBG) 传感器,实现裸光纤800 ℃内的应变测量(<1 000 με)。张开宇等[11]通过设计基底和光栅刻写工艺,增加了FBG 传感器应变灵敏度,应变测量误差小于3 με(0~700 με)。LI Ruiya 等[12]结合矩阵方法设计应变放大模型,应变灵敏度增加了6.34 倍,理论上达到温度解耦。杨润涛等[13]制备了表贴式Ⅱ型FBG 传感器,达到400 ℃的应变检测。申佳鑫等[14]提出一种FBG 和空芯光纤多模干涉效应的混合型温度-应变双参量传感器,通过耦合矩阵获得温度/应变数值。上述文献开展了FBG 的多场耦合测试及特种光纤光栅的制备,但多数研究更侧重理论方面,且特种光纤制备较难在工程上实现。
另一方面,FBG 传感器与基材的集成形式对应变测量结果有很大影响。权志桥等[15]通过推导表贴式FBG 传感器应变耦合分离式模型,得到修正关系,并通过试验得到验证。易志雄等[16]通过剪滞理论推导出表面粘贴式FBG 传感器最优胶层参数组合,并结合理论推导、有限元仿真验证了三者的相关性。孙丽等[17]开发一种3D 打印的封装层FBG 传感器,并探究胶层对应变测量的影响。而在实际工程应用上,较难对胶层的厚度、形状控制到毫米级以下精度,因此理论推导结果的工程实现性需要进一步解决。
针对以上问题,本文提出一种夹持粘贴式与温度补偿的FBG 传感器力热耦合测试方法,通过有限元仿真对比夹持粘贴与表面粘贴两种形式的应变传递率,分析标距比对夹持粘贴式应变传递率的影响,基于仿真结果选取夹持粘贴式的基本参数。在力热耦合实验中,集联一根FBG 温度传感器,实现250 ℃内,对3 000 με 内的解耦。通过高温试验验证了夹持粘贴式的测试准确性与工程实用性。
1 光纤光栅温度/应变传感与解耦原理
FBG 传感器中光栅是能够反射特定波长的无源器件,当宽带光源经过光栅时,满足条件波长的光被反射,其余的光则被透射出光栅。FBG 传感器光栅的中心波长表达式为
式中,λB为光纤光栅中心波长,neff为光栅有效折射率,Λ为光栅周期。
当环境中温度、应变等参量发生变化时,光栅周期和有效折射率受到影响,导致中心波长发生变化,即为FBG 传感器可以反映外界环境变化的原理,有
式中,ΔλB为光纤波长变化,ΔΛ为环境因素造成的光栅周期变化,Δneff为环境因素造成的有效率折射率变化。
当FBG 传感器所在环境中仅温度发生变化时,热光效应与光纤材料热膨胀效应会分别导致光栅的有效折射率neff和光栅周期Λ发生变化,从而使得中心波长发生变化,即
式中,Δλ为光纤中心波长变化,KT为光纤光栅的温度灵敏度,ΔT为温度变化。
当温度保持恒定,FBG 传感器受轴向力作用时,光纤拉伸变形导致光栅周期Λ变化,弹光效应导致纤芯的有效折射率neff变化,从而使得中心波长变化,即
式中,Kε为光纤光栅的应变灵敏度,Δε为应变变化。
根据传感理论得知FBG 传感器同时对温度/应变变化响应,忽略耦合效应,光纤光栅中心波长的变化量为
式中,Δλb1为温度/应变同时响应的FBG 传感器波长变化,KT1为该FBG 传感器的温度灵敏度,Kε1为该FBG传感器的应变灵敏度。
基于温度补偿的FBG 传感器温度解耦方法是引入一个只响应温度的FBG 传感器,该传感器的光栅中心波长变化量为
式中,Δλb2为只响应温度的FBG 传感器光栅波长变化,KT2为该FBG 传感器的温度灵敏度。温度与应变对光纤光栅中心波长为独立作用,线性叠加,联立式(5)、(6)解得独立应变为
式中,两FBG 传感器处于同一温度场中,可视为两光纤光栅温度响应相同,即ΔT相同。一般的裸光纤光栅传感器温度/应变灵敏度与光纤材料、写入工艺以及退火工艺有关[18],另一方面,将光纤光栅传感器与基材集成后,粘贴形式与基材属性对光纤光栅灵敏度影响也比较大,因此在实际使用中光纤光栅传感器应变/温度灵敏度需要通过集成后标定确定,并通过高温拉伸试验获取Δλb1和ΔT数据,利用式(7)解耦可得到应变数据。
2 裸光纤夹持粘贴式方法与仿真分析
2.1 夹持粘贴式/表面粘贴FBG 传感器应变传递率对比
光纤光栅传感器的抗剪强度低,极易折断。在使用时,需与测试件进行粘贴以达到测试与保护的目的,但是胶层会导致应变传递产生损耗,应变传递率α是光纤应变(εg)与待测基材应变(εi)的比值α=εg/εi,可以体现应变测试的准确性与灵敏性,因此首先分析不同粘贴工艺对应变传递率的影响。
夹持粘贴式FBG 传感器集成如图1 所示,将胶层均匀覆盖在光栅区外的两端光纤表面,光栅段光纤不直接承受外力,基材受力后,通过胶粘剪切应力传递光纤上的为轴向应力。表面粘贴FBG 传感器集成如图2 所示,将胶层均匀的覆盖在整段光纤的栅区部位,将基材与光栅融为一体,基材的应变通过胶体直接传递到FBG 传感器。
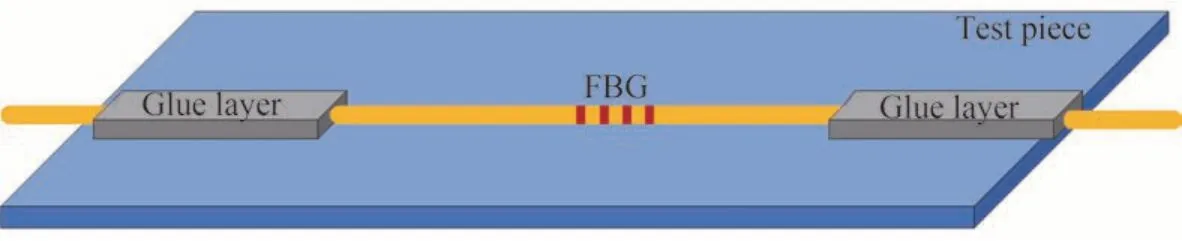
图1 夹持粘贴式FBG 传感器集成示意图Fig. 1 Schematic diagram of the integration of the clamp-adhesive FBG sensor

图2 表面粘贴式FBG 传感器集成示意图Fig. 2 Schematic diagram of the integration of surface-adhesive FBG sensor
为了对比两种FBG 传感器与基材集成方式,通过Abaqus 有限元分析对比两种粘贴方式的应变传递率。使用哑铃型304 不锈钢基材作为试验件,基材矩形段尺寸长×宽×高为80 mm×12 mm×1.5 mm,并选取CBK 高温胶作为裸光纤与基材的粘胶,相关的材料属性如表1 所示。

表1 材料属性Table 1 Material properties
设置胶层尺寸长×宽×高为20 mm×5 mm×1 mm,FBG 传感器半径为0.062 5 mm,光栅长度为10 mm。图3(a)中,将胶层覆盖在光栅两侧,胶层间距离为60 mm,模拟夹持粘贴式FBG 传感器的结构形式。图3(b)中,将胶层覆盖在光栅所在的光纤处,模拟表面粘贴式FBG 传感器的结构形式。对模型施加载荷,考虑基材试验时实际受力情况,选择基材上端圆内表面施加竖直向上的拉伸载荷,施加位移为0.6 mm,速度为0.003 mm/s,并对X和Z轴方向的位移进行限制,在下圆孔内表面施加完全固定约束。最后对模型进行网格划分(网格类型为:C3D8R),以及求解与后处理,选择E22(Y轴方向)方向的应变云图,如图4所示。

图3 模型的网格划分及载荷分布Fig. 3 Meshing of the model and load distribution

图4 仿真应变云图与应变数据Fig. 4 Simulated strain cloud maps and strain data
图4(a)、(b)为Y方向应变云图,可以看出,基材矩形段变形均匀,应变大小基本一致。图4(c)是基材、两种粘贴集成方式的光纤的应变数据,在仿真时间段内,三条应变曲线呈线性增加,将同时刻两种粘贴形式得到光纤光栅传感器应变数值与基材应变数值的比值视为应变传递率。由图看出夹持粘贴方式应变曲线与基材应变曲线基本贴合,其应变传递率为99.47%,而表贴式应变传递效率为95.8%。
从仿真结果可以看出,在该仿真条件下,夹持粘贴式FBG 传感器应变传递率高于表面粘贴式FBG 传感器,另外,表面粘贴式的FBG 传感器胶体覆盖光栅,在高温环境中,胶层材料属性发生变化,对光栅的反射产生较大的影响,甚至胶体渗入光栅间隙会使得光栅失效,对应变测量产生较大的影响。
2.2 标距比对应变传递影响分析
从仿真结果来看,夹持粘贴FBG 传感器的应变传递率虽然优于表面粘贴式,但其应变传递仍受胶层影响较大,通过胶粘应变传递理论与有限元仿真分析胶粘尺寸的影响因素。图5 为夹持粘贴式FBG 传感器的整体受力示意图,A 段粘贴受力,暂不考虑胶层的轴向变形,B 段属于自由拉伸段,光纤光栅不直接承受外力。

图5 夹持粘贴式FBG 传感器受力示意图Fig. 5 Schematic diagram of the force applied to the clamp-adhesive FBG sensor
文献[19]通过弹性力学理论与剪滞理论分析得光纤B 段应变传递率为
由式(8)可看出,在FBG 传感器以及胶层材料确定的情况下,夹持粘贴式FBG 传感器的应变传递率与标距比系数、胶层几何形状有关。由于粘胶有一定流动性,胶层几何形状精度较难在工程操作中保证,本文默认为光栅两侧胶粘形状为精度在1 mm 范围内相同的长方体,仅讨论标距比系数对应变传递率的影响,标距比系数由标距比决定,即自由段光纤(B 段)与粘贴段光纤(A 段)长度之比(LB/2LA)。通过固定胶层长度,改变胶层粘贴位置可以改变标距比,实现应变传递率变化,在工程操作中较好控制。
为了获得较好的应变传递率以指导基材与FBG 传感器的集成,使用Abaqus 有限元分析标距比对应变传递率的影响。采用有限元软件改变模型胶粘的位置从而改变标距比,并通过施加载荷,可以获得基材与光纤的应变,在理论上得到夹持粘贴式应变传递率。
设定光纤光栅区长度为10 mm,胶层长×宽×高尺寸为20 mm×5 mm×1 mm,自由段(B 段)光纤长度分别设为20 mm、40 mm、60 mm、80 mm、88 mm 和100 mm,得到不同标距比下的应变变化云图。
图6 为选取标距比为0.5、1 及1.5 的有限元网格及应变云图。提取标距比从0.5 到2.5 得到基材轴向应变与光纤轴向应变的数据,分别计算应变传递率,如图7 所示。

图6 不同标距比有限元网格与应变云图Fig. 6 Finite element mesh with strain cloud for different scale ratios

图7 应变传递率与标距比关系Fig. 7 Relation between strain transfer rate and scale ratios
从图7 可以看出,随着标距比的增大,应变传递率减少,当标距比大于1 时,应变传递率下降速度增大,为了测得准确的基材应变,应尽量降低标距比。当标距比小于1 时,应变传递率应变率差值约为0.1%。考虑FBG 传感器光栅的长度、胶层粘贴可操作性以及基材的尺寸,选用标距比1 进行操作。
根据仿真结果,本文FBG 传感器集成方式选用夹持粘贴方法,结合FBG 传感器的光栅长度为10 mm 和基材矩形段长度为80 mm,设定光纤自由端长度为30 mm,胶层长度为15 mm,标距比为1。另外,根据仿真结果,基材矩形段变形均匀,因此将FBG 应变传感器、高温应变片布置在基材矩形段中部可以进行相互验证。
3 传感器与基材集成制作与试验验证
为了验证夹持粘贴集成方式的工程实用性,以及温度补偿法解耦温度的效果,利用夹持粘贴方法以及选取的标距比将FBG 传感器集成于基材上,结合光纤光栅的温度、应变标定实验,以获得灵敏度。最后通过250 ℃内3 000 με 单向拉伸试验,并利用温度补偿的解耦方法获得高温下光纤光栅测量的应变值。
3.1 FBG 传感器与基材集成
列举一组FBG 传感器、高温应变片与基材集成粘贴的操作方法:先给光纤光栅传感器(FBG1)施加一定预应力,再根据2.2 节标距比参数,用CBK 高温胶粘贴覆盖光纤光栅区两侧各15 mm,光栅区保留30 mm自由段区,使用刮胶板刮匀胶层,并使用重物轻压胶层,保证胶层紧紧粘贴在基片上。同时,高温应变片和温度补偿的光纤光栅传感器(FBG2)固定在FBG1 旁。这样可以保证FBG 传感器的波长变化与基材应变变形呈线性关系,并保证FBG 传感器与高温应变片在同一变形区与同一温度场中。操作完成后试验件如图8所示,可以看出,由于CBK 高温胶的流动性,光栅区左侧长度为18.5 mm,右侧为16.0 mm,光栅自由段长度为30 mm,整个胶层厚度约为1 mm。长度、厚度尺寸与设定值存在一定的误差,标距比为0.87,这在手工操作中较难避免。

图8 FBG 传感器与基材集成Fig. 8 FBG sensor and substrate integration
3.2 温度/应变标定实验
标定试验可以获取FBG 传感器中心波长与温度、应变的线性关系,并且能确认FBG 传感器的精确度,为后续解耦奠定基础。
温度标定试验安排在集成试验件前开展,首先将两个FBG 传感器(FBG1、FBG2)使用高温胶带固定在基材上,使两个FBG 传感器保持松弛。将集成后的试验件放在加热平台(VECTCH, V-2020T)上,热电偶(KAIPUSEN,IN600-K)布置在两个FBG 传感器旁。设定温度为从室温到300 ℃,每隔50 ℃保持温度20 min,并进行温度数据采集。FBG 传感器与光纤光栅解调仪(大成科技,FT1601-31301)连接,获取中心波长的数据。经过多次试验,中心波长与温度的拟合曲线如图9 所示,相关系数R2≥0.99。其中一次拟合曲线的斜率设定为FBG 传感器的温度灵敏度,FBG1 与FBG2 传感器的温度灵敏度分别为KT1=12.393,KT2=12.293。

图9 温度标定Fig. 9 Calibration of temperature
应变标定实验是将FBG 传感器与基材集成后开展,首先将集成试验件安装上通用试验机(INSTRON,5982),设定0.01 mm/s 的速度拉伸试验件,拉伸长度为2 mm。FBG 传感器与光纤光栅解调仪(大成科技,FT1601-31301)相连,应变片(一洋测试,BAB120-3AA)与应变仪(协力科技,XL2101B4)相连,分别得到中心波长与应变数据,如图10 所示。经过多次试验,中心波长与应变的拟合曲线的相关系数平均R2≥0.99,其中一次拟合曲线的斜率设定为FBG 传感器的应变灵敏度,即Kε=1.596。
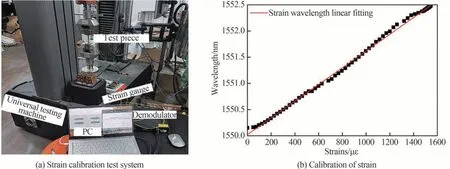
图10 应变标定试验Fig. 10 Strain calibration test
3.3 梯度高温拉伸应变试验
在完成温度/应变灵敏度标定基础上,开展不同梯度的高温拉伸试验。图11 为FBG 传感器高温应变试验系统,主要包括通用试验机(INSTRON,集成高温加热炉)、应变仪(协力科技,XL2101B4)、光纤光栅解调仪(大成科技,FT1601-31301)、热电偶(KAIPUSEN,IN600-K)、高温应变片(一洋测试,BAB120-3AA)以及PC 终端。

图11 试验系统与采集系统Fig. 11 Test system and acquisition system
高温炉与试验机集成,并提供高温环境,使用高温棉封住上下空隙,以保证炉内温度恒定,分别设置100 ℃、150 ℃、200 ℃及250 ℃四种温度梯度。固定试验件上下两圆孔,试验机以设定0.01 mm/s 的速度施加载荷,位移设置为4 mm。该试验平台提供了所需力热耦合环境,通过采集传输数据,进行数值的处理与分析对比。
3.4 结果与分析
温度梯度设置4 组不同的温度,分别为100 ℃、150 ℃、200 ℃和250 ℃,光纤光栅传感器的中心波长数据利用式(6)、(7)以及标定实验中的温度灵敏度、应变灵敏度进行解耦得到应变值,并与高温应变片采集数值对比,如图12 所示。从图中可以看出,应变的变化趋势有所差异是由于基片材料属性与轧制工艺存在些许不同,但FBG 传感器与高温应变片在时序上有较好的一致性,反映基材应变的变化趋势相同,且曲线具有较好的平滑度。

图12 高温拉伸试验结果Fig. 12 High temperature tensile test results
通过图12 可以看出,四种温度梯度下,平均相对误差分别为1.32%、1.62%、2.00%及2.26%;应变检测存在误差是由于光纤、应变片胶层无法完全保持一致,胶体的气泡也无法完全消除等因素导致。如图12 所示,四组温度的平均相对误差随着温度的升高逐步增大,这是由于覆盖应变片的胶体随温度增加粘贴效果逐渐变差。总体来看,平均相对误差最大值为2.26%,说明在250 ℃、3 000 με 范围内,光纤光栅传感器应变测试误差较小。由此可以得出提出的夹持粘贴式FBG 传感器可在一定高温下用于应变测量,并具有较高准确性。
测试结果在高温下应变解耦最大值可达2 810 με,与文献[10]、[11]的应变测试域对比,高出一倍以上;同时,对比文献[16]表面粘贴式FBG 传感器的应变传递理论分析,本文的夹持粘贴式FBG 传感器工程可操作性较高。
4 结论
本文针对力热耦合环境中的应变准确测试问题,首先通过Abaqus 有限元仿真,对比夹持粘贴式和表面粘贴式的应变传递率,前者应变传递率达到99.47%,后者为95.80%,可以看出,FBG 传感器与基材夹持粘贴集成可获得较准确的应变值。在夹持粘贴方式基础上改变胶层位置,得到不同标距比对应变传递率的影响,随着标距比增大,应变传递率降低。当标距比大于1,应变传递率下降速率明显增大。采用标距比为1 的夹持粘贴式光纤光栅传感器进行梯度高温拉伸试验,在温度/应变单独标定基础上,采用集联光纤光栅的温度补偿解耦方法,获得梯度高温下光纤光栅应变值。与标准高温应变片的平均相对误差最大值为2.26%,基本满足在工程上使用的需求。
另外,本课题所采用的FBG 传感器拉伸应变可达到11 000 με,但FBG 传感器需施加一定预应力后粘贴在基材上,会导致应变检测范围降低。后续将从光纤的材料与制作工艺上开展研究,并通过设计传感器基片结构及材料选型,增加FBG 传感器的应变灵敏度,达到较大应变范围以及压缩工况下的结构变形检测。

