超高速快轴旋转圆形弹光调制技术研究
刘燕霖,张瑞,薛鹏,陈媛媛,王志斌,李孟委
(中北大学 仪器与电子学院, 山西省光电信息与仪器工程技术研究中心,太原 030051)
0 引言
微电子在线原位检测、捕捉材料物理生物瞬态机制的变化过程对高速测量的要求越来越高[1-3],传统广义椭偏测量技术采用旋转补偿器或者双补偿器的结构进行测量,时间分辨率只能达到秒级,测量速度受限。弹光调制器(Photoelastic Modulator, PEM)作为一种光学谐振式偏振调制器件,具有调制速率高(数十kHz至数百kHz)、稳定性好(工作在谐振状态)等特点[4-6]。当PEM 处于谐振状态时,压电驱动器的逆压电效应使得弹光晶体内部出现双折射现象[7-8],从而对通过弹光晶体的光信号进行相位调制。
2010 年,PETKOVSEK R 等开发了基于PEM 的高速穆勒矩阵部分元素椭偏测量方法,时间分辨率可达30 μs[9],但该方法无法实现全穆勒矩阵16 个元素的测量;2012 年,ORIOL A 等通过使用4 个PEM 实现全穆勒矩阵椭偏测量,时间分辨率可达0.7 s[10],但结构较为复杂;2014 年,LÓPEZ-TÉLLEZ J M 等通过液晶可变相位延长器(Liquid Crystal Variable Retarder,LCVR)实现椭偏测量,但由于LCVRs 的调制频率较低,最终椭偏测量时间分辨率仅为2 s[11];2019 年EBNER A 等提出基于弹光调制的红外穆勒矩阵部分元素椭偏测量方法,时间分辨率优于1 s[12]。上述方法无法同时满足毫秒级时间分辨率和全穆勒矩阵广义椭偏测量。2020 年刘世元等提出基于双弹光偏振调制和分振幅偏振解调原理的高速全穆勒矩阵椭偏测量方法,时间分辨率可达11 μs[13],真正实现微秒级广义椭偏测量,但该系统需要6 个光电倍增管和多个分束镜,整个系统比较复杂。
为更进一步提高时间分辨率同时简化系统结构,本文介绍了一种更为对称的圆形PEM,当其工作在纯行波模式下,可用于替代旋转补偿器,调制频率可达60 kHz。利用COMSOL 仿真验证PEM 纯行波调制模式。基于纯行波调制模式的独特性质,提出一种中心支撑方式用于实验。
1 理论
1.1 弹光调制器纯行波理论分析
PEM 由两个压电驱动器和具有高度对称性的圆形弹光晶体胶合而成,两个压电驱动器之间的角度为45°。如图1 所示,A、B 表示两个压电驱动器,C 表示圆形弹光晶体。压电驱动器与弹光晶体具有相同的频率,并且高度耦合。压电驱动器在相同频率、任意相位的交流高压的作用下发生逆压电效应,迫使弹光晶体产生应变,由各向同性的弹光晶体变为单轴晶体。

图1 圆形PEMFig. 1 Circular photoelastic modulator
弹光晶体内部的应力驻波T可分解为沿逆时针方向和顺时针方向的应力行波,在极坐标系下可表示为
式中,TA、TB分别为A、B 两个压电驱动器在弹光晶体内部产生的应力幅值,应力幅值与驱动电压成正比;ω=2πft,f为PEM 谐振频率;t为时间;θ为极坐标下的空间位置,当cos2θ=±1 时为调制轴的位置,cos2θ=1时的位置为快轴的方向角,记为θ0;π/4 表示压电驱动器B 相对于压电驱动器A 的初始位置;φ表示A、B 两个压电驱动器上驱动电压的相位差。
式(1)展开得到
再经过三角变换可改写为
其中
当φ=±π/2 且TA=TB时,可将式(3)改写为
式中,“+”表示φ=π/2,快轴方向角为θ1=-πft,快轴方向角沿逆时针方向旋转;“-”表示φ=-π/2,快轴方向角为θ1=πft,快轴方向沿逆时针方向旋转。
由此得到,当两个压电驱动器上的电压幅值相等且相位差相差π/2 的奇数倍时,PEM 处于纯行波调制模式,可实现相位延迟量为常数,快轴方向角以f/2 角速率做圆周运动的偏振光调制。
当PEM 处于纯行波模式时,搭建如图2 所示光路验证光的偏振调制。其中,起偏器P2的偏振方向与激光器平行水平面之间的角度为θ0,检偏器P3的偏振方向与激光器平行水平面之间的角度为θ2,PEM 的快轴方向与激光器平行水平面角度为θ1,PEM 的相位延迟量为δ。

图2 系统光路示意图Fig. 2 Diagram of system light path
激光器发出的光束,经过偏振器P1后,输出为线偏振光[14]。用归一化的斯托克斯矢量可表示为
斯托克斯矢量求解方法为Sout=[I,Q,U,V]T=MP3(θ2)×MPEM(θ1,δ)×MP2(θ0)×Sin。其中,MP3(θ0)为检偏器P3的穆勒矩阵,MP2(θ0)为起偏器P2的穆勒矩阵,MPEM(θ1,δ)为PEM 的穆勒矩阵,分别为
代入求解得到Sout公式为
进而得到探测器归一化后光强电信号为
式中,设置θ0、θ2分别为180°和0°,当PEM 工作在纯行波模式时,快轴方向角沿逆时针方向旋转,θ1=πft,代入式(7)得到归一化的光强电信号为
当PEM 达到稳定的纯行波状态时,PEM 的相位延迟量δ趋于常数[15]。当探测器探测到光强信号中仅存在直流信号及二倍频信号时,PEM 实现纯行波偏振光调制模式。
1.2 弹光调制器纯行波仿真验证
PEM 的压电驱动器主要采用x-18.5°切型、长度伸缩模式优越的石英晶体,弹光晶体一般采用硒化锌或熔融石英材料,但硒化锌材料适合制作谐振频率大于等于27.1 kHz 的PEM,熔融石英材料适合制作谐振频率大于等于42.99 kHz 的PEM。本文拟制备频率为60 kHz 的PEM,因此选择x-18.5°切型的石英晶体为压电驱动器,熔融石英为弹光晶体。
PEM 工作在谐振基频,对于x-18.5°切型、长度伸缩模式优越的石英晶体,其谐振基频为
式中,l为石英晶体长度;ρ=2 684 kg/m³为石英晶体的密度;s22=14.454 4×10-12m2/N 为石英晶体坐标变换后的弹性柔顺系数。
因此,设计目标频率为60 kHz 的压电驱动器的长度约为42.31 mm。通过仿真得到压电石英晶体实际几何尺寸如表1。

表1 60 kHz 压电驱动器几何尺寸参数Table 1 60 kHz piezoelectric driver geometry parameters
二维圆形熔融石英材料的弹光晶体,其谐振基频为
式中,d为圆形弹光晶体的直径;E=70 GPa 为熔融材料的杨氏模量;v=2 203 kg/m3和ε=0.17 分别为其密度和泊松比。
因此,制备目标频率为60 kHz 的弹光晶体的直径为约为43.42 mm。通过仿真得到弹光晶体实际几何尺寸如表2。

表2 60 kHz 弹光晶体几何尺寸参数Table 2 60 kHz elastic crystal geometry parameters
接着,经过有限元仿真得到PEM 表面应力及表面振型,并且得到PEM 的谐振频率为60.001 kHz,如图3 所示。

图3 60 kHz 弹光调制器稳态仿真结果Fig. 3 Steady state simulation results of 60 kHz elastic light modulator
根据式(4),设置两压电驱动器上的驱动电压幅值相等,相位相差π/2,设置瞬态求解器进行求解,得到一个周期内快轴以f/2 的角频率做圆周运动,如图4 所示。
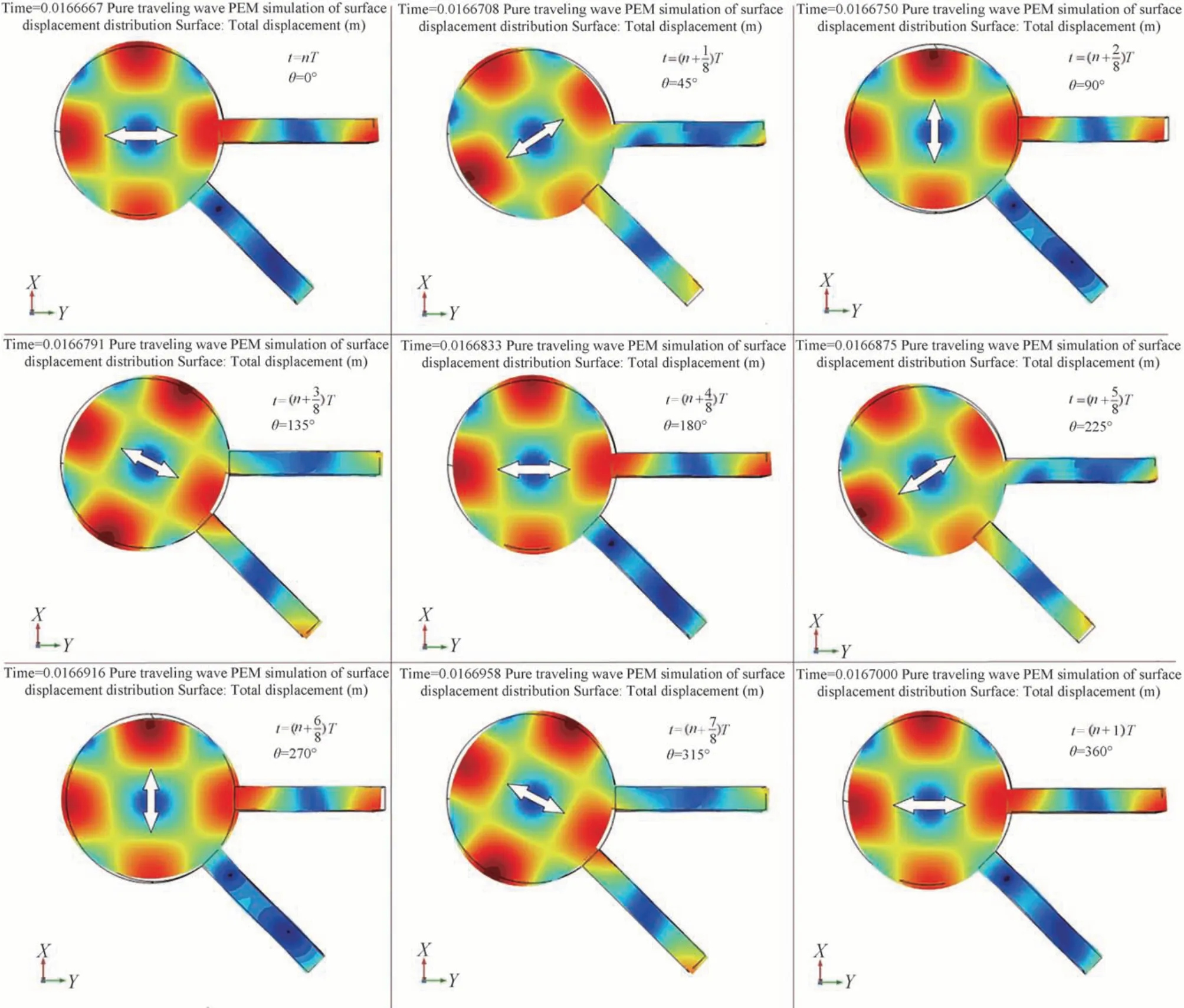
图4 一周期内PEM 振型及快轴方向Fig. 4 PEM Vibration mode and fast axis direction during the period
2 中心支撑方式研究
PEM 达到谐振后,振动平面处于二维平面。该平面的法线方向一般为光信号的入射方向,理想状态,该方向的受力不影响弹光晶体的振动。但实际使用支撑结构进行固定时,弹光晶体上二维振动平面会产生阻尼,将此种阻尼等效为阻尼弦振动。图5 为弦在某种介质中进行微振动,当弦处于理想状态(t=0)时,弦的两个端点固定在x=0 和x=L处,平衡位置为x轴。

图5 阻尼弦振动模型Fig. 5 Damped string vibration model
初始时刻弦处于平衡位置,振动时受到的阻力与振动速度成正比,单位长度弦受到的阻力可表示为
式中,“-”表示阻力方向与振动方向相反;k为阻尼系数;u(x,t)为弦的位移,表示弦离开平衡位置的位移量。
由式(9)可知,弦的速度越大,受到的阻力越大。因此,支撑结构的阻尼在弹光晶体振动位移大的区域产生阻力大,在弹光晶体振动位移小的区域产生阻力小。
根据图4 结果所示,当PEM 处于纯行波调制模式时,快轴方向角变化会引起弹光晶体振动位移变化。在一个周期内分别选取PEM 的快轴方向角为0°、22.5°、45°、67.5°的PEM 中弹光晶体振动位移如图6 所示。

图6 不同快轴方向下弹光晶体振动表面位移量Fig. 6 Vibration surface displacement of elastic crystal in different fast axis
根据不同快轴角度下弹光晶体位移量显示,弹光晶体的圆心区域振动位移量最小,沿着半径方向振动位移逐渐增大。虽然圆周振动位移量最大,但仍存在振动位移较小的区域。当PEM 的快轴方向角以f/2 的角频率作圆周运动时,弹光晶体圆周表面位移较小的区域会随着时间而改变,而弹光晶体圆心区域的位移量始终最小且保持稳定。因此,PEM 的圆心区域振动位移量最小,致使垂直支撑在震动方向上所引起的阻力最小。基于此,选取圆心区域为固定的最佳支撑位置。
根据理论分析设计了一种中心支撑装置,如图7 所示。弹光晶体的圆心位置设置了对称的两个通光孔,通光孔与弹光晶体表面接触用于固定PEM,根据弹光晶体的有效通光孔径,设置通光孔为7 mm。同时,为了减少因支撑对压电驱动器和弹光晶体表面造成损伤,在通光孔与弹光晶体接触表面和紧固件与压电驱动器接触表面放置一层具有缓冲作用的软性橡胶,厚度为1 mm 左右。

图7 新型支撑装置结构示意图Fig. 7 Structure diagram of the new support device
中心支撑方式充分利用弹光晶体在二维平面内振动时圆心区域振动位移量最小、弹光晶体表面振动位移分布随快轴方向角变化等特性,适用于PEM 纯行波调制模式,不影响快轴方向角的调节。
3 实验
为验证理论仿真的正确性及中心支撑方式的可行性,搭建如图8 所示的光路系统。采用632.5 nm 的激光器作为光源,P1为偏振器,通过改变偏振片P1与起偏器P2的通光轴夹角可减弱光强。探测器可以将输入光信号转为电信号。
利用信号发生器分别给两个压电驱动器A 和B 提供频率为60 kHz、幅值相同的驱动信号,同时利用放大器分别将该信号放大100 倍,通过不断调整信号频率进行扫频,最终得到两个压电驱动器的谐振频率为59.421 kHz,如图9 所示,其中,信道三所示为光强信号,信道一为左侧压电驱动器的驱动信号,信道二为右侧压电驱动器的驱动信号。
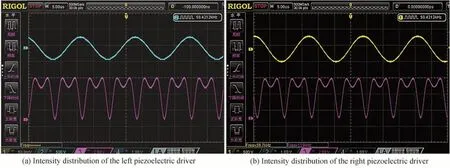
图9 两压电驱动器分别使PEM 达到谐振频率结果Fig. 9 The result of two piezoelectric actuator respectively bringing the PEM to the resonant frequency
设置光路中起偏器P2和检偏器P3的通光轴角度为90°和0°,两驱动电压的峰峰值为800 V 和800 V,同时将两驱动信号的相位在90°附近扫描,得到当两驱动信号相位差为92.3°时,光强信号为正弦信号,如图10 所示。依据第2 节理论推导,此时PEM 处于纯行波调制状态。接着,通过数据处理,得到经过快速傅里叶变换(Fast Fourier Transform,FFT)后的光信号如图10 所示,其结中只存在直流分量及二倍频分量,不存在其他分量。

图10 纯行波调制模式下信号及FFT 处理后信号Fig. 10 Signal in pure traveling wave modulation mode and signal after FFT processing
4 结论
本文提出一种对称结构圆形PEM 纯行波调制模式,可用于替代双旋转补偿器型广义椭偏仪中的相位调制器,进而实现超高速测量。通过COMSOL 仿真验证所提出的PEM 纯行波调制模式下快轴超高速旋转理论。同时,分析得到PEM 纯行波调制模式在不同快轴角度下弹光晶体表面的位移分布。通过建立阻尼弦振动模型,提出一种当PEM 振动时所受阻尼最小的中心支撑结构用于实验。利用傅里叶变化反演得到光的斯托克斯矢量,验证了PEM 纯行波调制模式的可行性。在接下来的研究中,将从应用的角度出发,将提出的PEM 相关技术与椭偏测量相结合,利用贝塞尔函数及各个器件的穆勒矩阵等参数反演得到样品的穆勒矩阵,最终实现样品厚度及相关偏振信息的超高速测量。

