GRIN 色散物镜光学像差对峰值波长提取的影响
李春艳,李丹琳,刘继红,李可,蒋杰伟
(西安邮电大学 电子工程学院,西安 710121)
0 引言
光谱共焦位移传感系统使用宽谱光源照射物体表面,利用光学色散原理使色散物镜产生轴向色差,建立色散距离与波长间的对应关系,利用光谱仪探测聚焦于物体表面并反射回来的光谱响应峰值波长,获得精确的轴向位置或微小位移数据,具有超高的距离测量分辨率,且对环境及材料具有广泛的适应性[1-3]。色散物镜是光谱共焦位移传感系统的核心器件,系统的测量精度与色散物镜的分辨率有着密切的关系,测量值的精确度和测量范围取决于色散物镜轴向色散的大小,而色散物镜的光学像差影响聚焦波长的轴向分布,对采集的光谱响应数据产生干扰,进而影响系统的测量性能[4-6]。梯度折射率(Gradient Index,GRIN)透镜具有多自由度的折射率参数,其效果等同于多面型复杂、工艺要求和成本较高的匀质光学元件,具有几何形状简单、重量轻、体积小、光学性能优良等特点,且便于光学集成[7-10]。SARAH L 等[11]提出使用衍射光学元件为色度深度测量提供聚焦波长编码,利用衍射透镜进行波长的深度编码和非机械深度扫描,在100 nm波段范围轴向色散达到55 μm。LIU Q 等[12]使用的FK7l、LAF4 和ZF72A 玻璃分别产生线性正色散和负色散,在430~710 nm 波长范围内,产生了1 mm 的轴向色散。MA J 等[13]根据光谱共焦位移传感器的工作原理和轴向色散条件,选用3 种玻璃材料N-KZFS11、N-SF66 和N-PK52A,结合三个单透镜和两个双胶合透镜,在450~650 nm 波长范围内,设计出了轴向色散约为1 050 μm 的色散物镜。在上述研究中,色散范围满足设计要求的组合系统的线性度较差,影响了系统的灵敏度和测量精度。
使用小口径色散物镜光谱共焦位移传感系统可以不受色散物镜轴向色散大小的限制,深入产品获得合适的工作距离,间接扩大传感器的测量范围,因此,针对小孔内径或产品内部缺陷检测的应用需求,在GRIN透镜研究的基础上[14-17],本文利用GRIN 透镜设计了微小口径色散物镜。为分析GRIN 色散物镜光学像差对峰值波长提取的影响,实现基于GRIN 色散物镜的光谱共焦位移传感系统的性能优化,研究了GRIN 色散物镜的光学像差对峰值波长提取的影响,并建立了光学像差拟合算法。首先,利用傅立叶光学的波前像差方程,结合GRIN 色散透镜的折射率随不同波长以及曲率半径的变化,在光谱共焦垂直采样序列中分别建立GRIN 色散物镜的球差、像散以及彗差的物理模型进行研究与分析。其次,模拟仿真了球差、像散以及组合像差对峰值波长偏移的影响。最后,通过高斯拟合、Zernike 多项式拟合以及sinc2函数拟合三种方法对不同像差情况下的轴向响应信号进行了数据拟合。
1 GRIN 色散透镜的光学性能
光学像差在光学系统中不可避免,其畸变率通常在出瞳孔或聚焦区进行分析。在出射光瞳处,比较真实波阵面和理想球面波阵面来评估像差[18]。在基于傅立叶光学的非均匀化成像模型中,衍射效应是由出射光瞳产生的,因此可以求出轴向响应信号的像差,将波前像差加入出射光光瞳函数中。在光谱共焦技术中,轴向响应信号记录在不同的垂直扫描位置,即垂直采样序列。具有等距间隔的广义序列为
式中,n和m为整数,其中Uj是垂直采样序列中扫描截面的位置,j=-n,…,m,垂直采样序列中的间隔是垂直扫描装置的扫描步长ΔU。样品表面高度为待测样品表面与参考点之间的相对距离,在不失真的情况下,选择垂直采样序列上的一个点作为参考点。
由GRIN 材料折射率分布常数[19]可得GRIN 色散透镜的折射率分布为
式中,n0表示透镜顶点处的折射率,λ为波长,r为透镜半径。
径向GRIN 透镜内部的折射率分布沿径向梯度变化,有聚焦成像的特点,因此又称为自聚焦透镜,设计径向平凸GRIN 色散透镜几何结构如图1(a)所示,半径为r,曲率半径为RG,透镜中心厚度为tc,直径为D,焦距为f,当GRIN 透镜半径r=0 时,透镜顶点处的折射率n0=1.651。在波长λ1=486 nm,λ2=587 nm,λ3=656 nm 时,梯度折射率半径与折射率之间的关系如图1(b)所示。
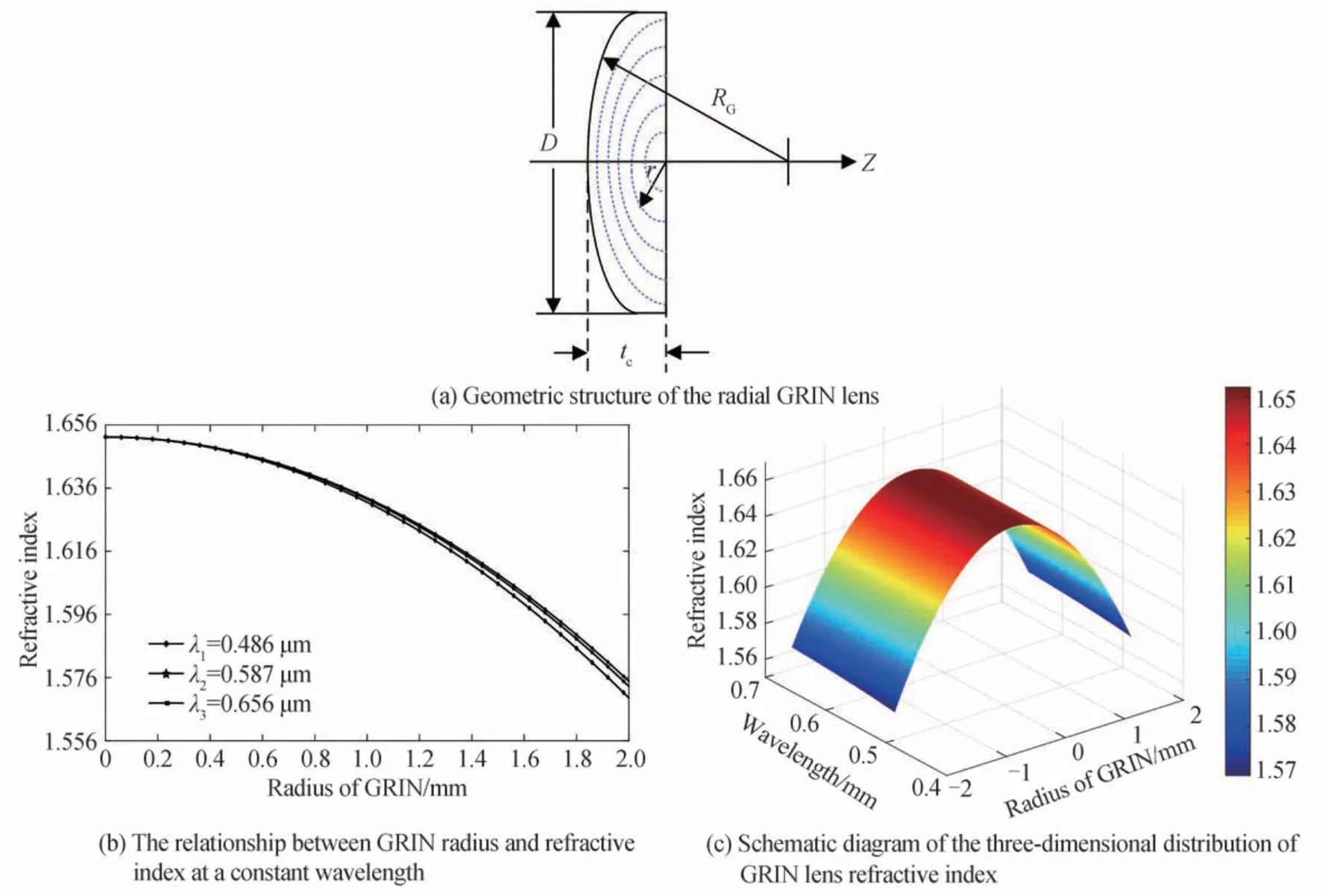
图1 径向平凸GRIN 色散透镜结构及梯度折射率半径与折射率之间的关系Fig. 1 The radial GRIN dispersive lens structure and the relationship between the gradient refractive index radius and the refractive index
从图1(b)中可以看出,波长分别为λ1=486 nm、λ2=587 nm、λ3=656 nm 时,折射率均随GRIN 半径的增大而减小,在轴心处折射率最大,满足设计要求。此外,使用MATLAB 对GRIN 透镜折射率分布示意图进行了三维仿真,如图1(c)所示,可以看出GRIN 透镜的折射率随不同波长以及曲率半径的变化关系为:光轴原点处的折射率最大,且呈抛物线分布,在波长恒定的情况下,折射率随GRIN 透镜的半径增大而减小。根据Go-Foton 公司[19]的GRIN 材料折射率分布常数清晰反映出的光学系统波长、GRIN 半径与折射率之间的内在关系,利用式(2)获得GRIN 色散透镜轴向色散对应的波长λ与位移数据Z(λ)如表1 所示。

表1 GRIN 色散透镜轴向色散对应的波长λ 与位移数据Z(λ)Table 1 The wavelength λ corresponding to the axial dispersion of the GRIN dispersion lens versus the displacement data Z(λ)
2 像差对GRIN 色散物镜峰值波长提取的影响
光谱共焦位移传感系统轴向响应信号峰值波长提取的准确性对保证系统测量精度具有重要意义,而色散物镜光学系统的像差会对轴向响应信号产生影响,引起峰值波长偏移,使测量数据发生漂移。在实际系统应用中,色散物镜产生的轴向色散实现波长与位置之间的精确编码,通过解码轴向响应峰值波长获取位置信息。因此,研究色散物镜光学像差对峰值波长的影响,对进一步提高系统测量性能具有一定的指导意义。
2.1 GRIN 色散物镜的设计
根据光谱共焦位移传感系统的工作原理以及色散物镜产生轴向色散的条件,对GRIN 色散物镜进行设计。首先结合光学系统的像差理论对玻璃材料进行选择,保证轴向色散的同时提高色散与波长之间的线性关系;另外,色散物镜光学系统成像聚焦在光轴上,轴外像差可以忽略不计。为了控制系统像差,采用径向GRIN 色散透镜与双胶合透镜组合的方式进行设计,可以通过分散系统的光焦度有效降低光学系统的球差;此外,选择种类不同的透镜材料可以提高光学系统的线性度。为满足以上条件,采用径向GRIN 透镜作为单透镜,在ZEMAX 玻璃库中使用Gradient 6,双胶合透镜采用Schott 玻璃库中的H-FK61、H-F51、H-ZF62。
径向GRIN 色散物镜的波长设置为可见光波段,入瞳直径设置为2 mm,视场角设置为归一化视场坐标,波长与轴向色散之间的线性系数需满足色散物镜的线性度,提高分辨率,保证系统测量精度。GRIN 色散物镜的初始结构如图2 所示。

图2 GRIN 色散物镜的初始结构Fig. 2 Diagram of the initial structure of the GRIN dispersive objective lens
在光学设计软件ZEMAX 中对GRIN 色散物镜光学系统进行优化设计,在保证波长与焦移线性度的同时,提高镜头的聚焦特性,降低球差。优化过程中采用ZEMAX 操作数控制参数变化,使用AXCL 对光学系统产生的轴向色差和线性度进行控制;使用CONF 对系统全局结构进行优化;其中径向平凸GRIN 透镜在设计过程中采用COVA 圆锥系数得到平凸结构;使用LONA 对系统球差进行控制。采用近轴系统进行设计,使用EFFL 控制有效焦距;使用IMAG 设置镜头分辨率,优化后的GRIN 色散物镜结构如图3(a)所示[17,20]。波长聚焦能量如图3(b)、(e)所示,主要采用点列图进行光学系统像质评价,可以看出,点列图中弥散斑半径均小于艾里斑半径,镜头聚焦效果良好,几乎所有的光线都在艾里圆环内,系统达到衍射极限,符合设计要求。
优化后,在ZEMAX 中获得轴向色散与波长之间的数据关系如图4(a)所示,可知GRIN 色散物镜产生的色焦移约为1 215 μm,即色散范围超过了1 mm。对波长-焦移曲线数据使用最小二乘法进行线性拟合,拟合结果如图4(b)所示。
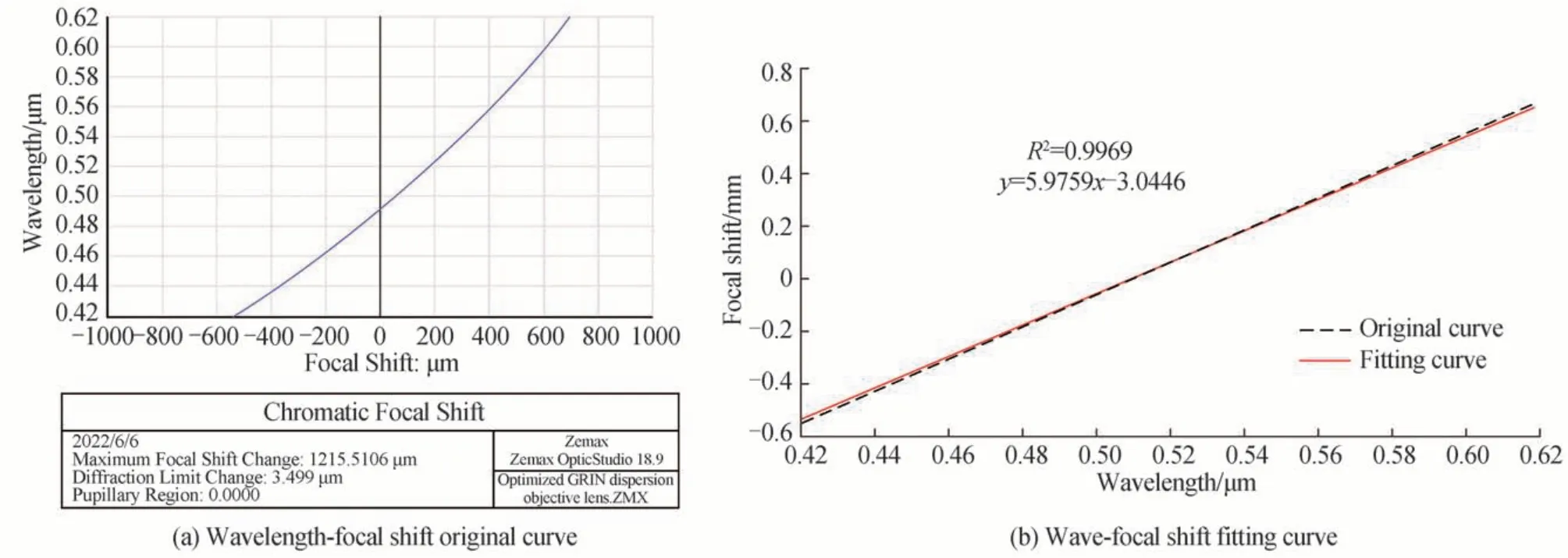
图4 波长-焦移关系及拟合曲线Fig. 4 The wavelength-focal shift relationship and the fitted curve
通过图4(b)可知,波长与轴向色散的线性相关系数为0.996 9,光学系统的线性度良好,系统分辨率约为6.075 nm,测量范围较大的同时保证了色散物镜良好的线性度,满足设计要求。将色散物镜的成像用傅里叶光学[21]表示为
式中,I(x)表示光谱图像强度,T(v)表示空间频率v的函数,为透射光谱函数,b(v)为相关传递函数,有
P(v)为色散物镜的光瞳函数,⊗表示卷积。
为了研究像差对峰值波长提取的影响,在色散物镜的光瞳函数中引入相位因子
式中,函数W(σ,θ)表示像差相位函数,σ为出瞳的归一化半径,θ为归一化场矢量与出瞳处归一化半径矢量之间的径向角,u为实际轴向距离z和主波长λ相关的垂直位置处的光学坐标,即
α为孔径角。
在后续的研究中,主要以主波长λ为研究对象,分析不同像差对波长提取的影响。此时,W(σ,θ)可以表示为
式中,WSA为球差系数,WC为彗差系数,WA为像散系数。
为分析GRIN 色散物镜光学像差对峰值波长提取的影响,GRIN 色散物镜的光瞳函数为
在理想状态无像差时,式(8)可以化简为
但在实际应用中,光学系统不可能为无像差系统,因此式(9)并不能在实际系统中应用,需利用式(8)分析各个像差的影响。
2.2 球差对峰值波长的影响
首先研究球差的影响,由于球差是轴上像差,光瞳函数可以化简为
根据菲涅尔积分可知
式中
对式(12)进行傅里叶级数展开
因此
基于式(10)和(14),对球差分别为0、0.2、0.4、0.6、1、2、3 时的单峰轴向响应峰值波长进行仿真分析,获得不同球差对单峰轴向响应峰值波长的影响如图5 所示,其中横坐标为垂直位置处的光学坐标,纵坐标为归一化强度。

图5 不同球差对单峰轴向响应峰值波长的影响Fig. 5 The effect of different spherical aberrations on the peak wavelength of single peak axial response
图5(a)为球差分别等于0、0.2、0.4、0.6、1 时单峰的轴向响应峰值波长的偏移情况,图5(b)为球差等于2和3 时的轴向响应峰值波长。可以看出不论是否存在球差,主峰和旁瓣基本对称。球差越大,峰值波长偏移的越多,越远离中心轴线u=0,球差为1 时,峰值波长偏移6.28 nm;同时随着球差的增大,峰值旁瓣逐渐变大,并且对峰值影响较大,球差为2 和3 时出现了混乱的双峰,因此,球差越大对峰值波长提取的影响越大。
2.3 像散对峰值波长的影响
存在像散时,GRIN 色散物镜的光瞳强度函数可以表示为
化简得
根据菲涅尔积分,式(16)可写为
其中,
对式(18)进行傅里叶级数展开
基于式(16)和(17),对像散分别为0、0.5、0.7 和0.9 时的轴向响应峰值波长进行仿真分析,获得不同像散引起的轴向响应峰值波长偏移如图6 所示,其中横坐标为垂直位置处光学坐标,纵坐标为归一化强度。
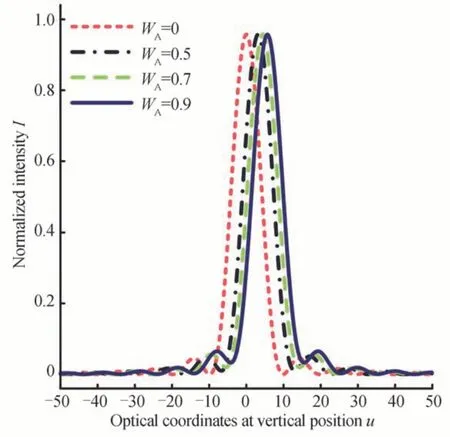
图6 不同像散引起的轴向响应峰值波长偏移Fig.6 Peak wavelength shift of axial response due to different dispersion
由图6 可以看出,不论像散的大小为多少,轴向响应峰值波长分布曲线始终对称;与球差相比,像散增大引起的峰值波长偏移不是很明显,说明像散对峰值波长偏移的影响没有球差的影响大。
2.4 彗差对峰值波长的影响
利用彗差存在时的光瞳强度函数进行分析,计算传递函数所需的光瞳函数的几何重叠如图7 所示。

图7 光瞳函数的几何重叠Fig.7 Geometric overlap of pupil functions
通过式(5)和(7)对式(4)所求的卷积函数表示像差的传递函数b(v),即
式中,S表示传递函数的等距曲面。
式中,v͂表示像差存在时的空间频率。因此,可以推导出
式(20)可化简为
由式(23)的传递函数表达式可知,当v͂=0 时,慧差不会影响传递函数b(v,u,WSA,WA,WC),因此峰值波长不受彗差的影响。同理,场曲、畸变均为轴外像差,也不会引起峰值波长偏移。
2.5 球差和像散对峰值波长的影响
当球差和像散同时存在时,组合像差引起的轴向响应峰值波长偏移如图8 所示,其中WSA=1,WA=1。

图8 组合像差引起的轴向响应峰值波长偏移Fig. 8 Peak wavelength shift of axial response due to combined aberration
由图8 可知,组合像差对峰值波长的影响最大,不仅对称轴产生了较大幅度的曲线偏移,同时出现了三峰,旁瓣升高,且分布不对称,打破了单像差存在时的对称分布规律;结果表明GRIN 色散物镜组合像差会引起较大的光谱共焦位置偏差或系统误差。
3 峰值波长提取拟合算法
光谱共焦位移传感系统基于色散物镜对波长与位置之间的编码关系,通过解码轴向响应峰值波长进行位移测量或表面位置信息的获取。因此,快速、准确、高效的峰值波长提取是保证系统测量精度的必要前提。通过比较不同峰值波长提取算法的拟合效果,选择最佳算法。
3.1 高斯拟合
高斯拟合[22]是根据高斯算法对数据进行曲线拟合的方法,拟合函数为
式中,ymax为峰值,xmax为峰值位置,M为峰值半宽度,对式(24)取对数得
假设,
则式(25)可化简为
将式(27)用矩阵形式表示并记为G=XB,则
根据矩阵原理,可以写为
根据以上分析对球差分别为0.2 和0.4 时的轴向响应信号进行高斯拟合,结果如图9 所示。

图9 轴向响应信号的高斯拟合Fig. 9 Gaussian fitting of the axial response signal
根据图9 可以看出,高斯拟合算法能够对整个曲线进行较好的拟合,峰值提取误差较小,但整个拟合过程中对旁瓣的拟合效果不是特别好。由于本文使用的高斯拟合算法是最小二乘法拟合,它是通过对非线性高斯函数进行化简,将非线性高斯函数转换为线性函数,再通过最小二乘法进行对数运算,从而完成高斯拟合的计算。所以在拟合线性度较高的峰值波长数据的过程中可以准确地进行拟合,在对非线性旁瓣进行拟合时,该方法的拟合效果不是很理想。因此,高斯拟合提高了峰值波长的提取精度,但是对旁瓣的拟合处理相对较差。
3.2 Zernike 多项式拟合
Zernike 多项式拟合方法[23]广泛应用于光学像差分析,光学系统的像差函数可以表示为
式中,n和m分别为多项式的径向数与角向数,且同时满足n≥0,m≥0,n≥m,n-m为偶数多项式为
式中,δmn为Kronecker 符号,多项式的径向函数为
式中,s为Zernike 多项式的序号,正交Zernike 表示为
式中,n'和m'分别为理论上的径向数与角向数,当n=n'时,δnn'=1;当n≠n'时,δnn'=0,δmm'同理。
在光谱共焦位移传感系统中,像差W(σ,θ)可以依据Zernike 多项式表示为
式中,Zi是多项式的第i项,ci表示对应的系数,N为总项数,因此Zernike 多项式的展开系数可以表示为
根据以上分析,对球差分别为0.2 和0.4 时的轴向响应信号进行Zernike 多项式拟合,结果如图10 所示。

图10 轴向响应信号的Zernike 多项式拟合Fig. 10 Zernike polynomial fitting of axial response signal
由图10 可以看出,Zernike 算法基本上可以对整个曲线进行完整的拟合,峰值提取误差较小,对旁瓣也可以实现比较完整的拟合。主要是由于Zernike 算法是线性模型拟合,Zernike 多项式模型和所需拟合的参数之间是线性关系,对被测区域进行分析处理构造多项式函数,且确保多项式函数尽可能近似地表达被拟合数据的输入输出关系。因此Zernike 算法不仅可以对线性度较高的峰值波长数据进行准确拟合,也可以对非线性旁瓣进行有效拟合。
3.3 sinc2拟合
sinc2函数[24]拟合首先通过对原始数据进行分析与载入,然后通过设置初始迭代值进行数据迭代拟合,对迭代过程设置终止条件,满足终止条件则终止数据迭代,从而对结果进行处理,结果输出;如果不满足结束条件,则返回上一步继续进行迭代,直至满足终止条件。sinc2函数的表达式为
式中,e、h分别为sinc2拟合函数模型参数,对球差分别为0.2 和0.4 时的轴向响应信号进行sinc2拟合,结果如图11 所示。
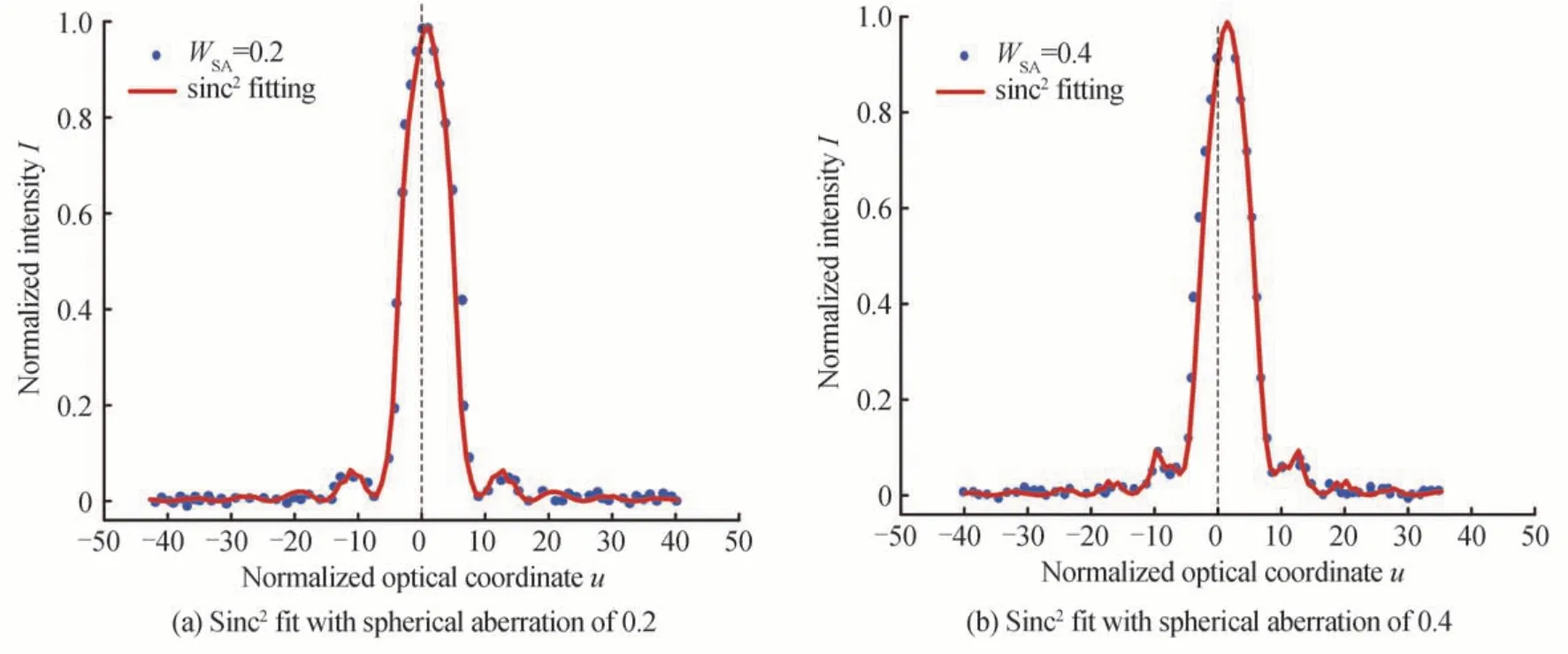
图11 轴向响应信号的sinc2拟合Fig. 11 sinc2 fitting of the axial response signal
如图11 所示,sinc2函数拟合利用目标函数的一阶和二阶导数信息迭代收敛,通过设置拟合参数的初始数据区域,对数据多次迭代进行拟合,最终得到拟合结果。通过图10(a)和(b)可以看出,原始蓝色波长峰值点和sinc2函数拟合结果几乎一致重合,能够实现波长与位置信息的精确转换,不仅对峰值具有较好的拟合效果,同时也能够实现旁瓣的精准拟合。因此,相比高斯拟合和Zernike 多项式拟合,sinc2函数拟合不仅对主峰进行良好的拟合,而且对旁瓣的拟合效果优于高斯拟合和Zernike 多项式拟合。
3.4 拟合算法误差分析
为获得更准确的峰值波长提取算法,在不同采样间隔ΔU和球差下进行了高斯拟合、Zernike 多项式拟合和sinc2拟合误差分析,对分别使用三种方法时的具体误差进行了计算,如表2 所示。

表2 不同像差时的拟合误差Table 2 The fitting errors at different aberrations
通过表2 可以看出,在球差为0.2 时,Zernike 多项式拟合的误差小于高斯拟合,sinc2拟合的最大误差为0.025 6±3.882×10-4,最小为0.003 8±3.781×10-5;而高斯拟合的最大误差为0.035 6±4.892×10-4,最小误差为0.012 2±1.257×10-5;Zernike 多项式拟合的最大误差和最小误差介于高斯拟合和sinc2拟合之间。当球差分别为0.6 和0.8 时,sinc2拟合的误差最小,在三种方法中具有最高的拟合准确性。因此,在进行GRIN 色散物镜光学像差影响下轴向响应的峰值波长提取时,高斯拟合的准确性最差,其次是Zernike 多项式拟合,sinc2拟合最准确。
4 结论
本文主要研究了GRIN 色散物镜光学像差对轴向响应峰值提取的影响。首先分析了GRIN 色散透镜的光学性能,给出了GRIN 透镜折射率与阿贝数之间的对应关系,同时分别仿真了特定波长下的GRIN 色散透镜半径与折射率之间的关系,获得了GRIN 色散透镜的轴向色散数据。其次,通过建立优化后GRIN 色散物镜的光学像差物理模型,研究并分析了球差、像散以及组合像差对峰值波长的影响。结果表明,球差和像散以及组合像差会引起轴向响应峰值波长偏移,球差为1 时,峰值波长偏移6.28 nm,球差大于1 时,出现双峰,球差越大引起的峰值波长偏移越大;像散对峰值波长偏移的影响小于球差;组合像差对峰值波长的影响最大,出现了三峰旁瓣同时升高,引起较大的光谱共焦位置偏差或系统误差,其中轴外像差的影响可忽略。最后,利用高斯拟合、Zernike 多项式拟合和sinc2函数拟合方法对不同像差影响下的轴向响应信号进行了数据拟合和拟合误差分析,结果表明,在进行GRIN 色散物镜光学像差影响下轴向响应的峰值波长提取时,sinc2拟合最准确。研究结果对建立像差影响的峰值波长提取误差修正和补偿算法,并进一步提高光谱共焦系统测量性能具有参考意义。

