基于局部焦距追迹计算优化的广角镜头设计方法

陈露，刘辉，封志明，陈熙源，张帆，许宁晏，袁群，高志山

（1 江苏省计量科学研究院（江苏省能源计量数据中心），南京 210023） （2 东南大学 仪器科学与工程学院，南京 210018） （3 南京理工大学 电子工程与光电技术学院，南京 210094）

0 引言

光线追迹是开展光学系统优化设计的基础手段。基于Snell 定律的光线追迹计算既可以获得光学系统的焦距、入瞳、F数等一阶参数，也可以获得各类型像差分量。相较于描述成像清晰度的像差，畸变最为特殊，它通过追迹各视场主光线在像面上的高度，计算与理想投影模型的偏差，描述物像映射的变形量［1-3］。投影模型规定了光学系统成像关系中物方视场角与像高的关系。常规的投影模型为等线投影映射，当光学系统的视场较大时，演变出了等距投影映射。体视投影映射、等立体角投影映射、正交投影映射也有相应复杂场景的应用［4-5］。显而易见，投影模型中物方视场角和像高由焦距相关联。

焦距是光学系统最基础的特性参数，其本征定义为像方主面与像方焦点之间的距离，通过追迹零视场小孔径近轴光线计算获取，该计算方式描述称为“小孔径法”。光学设计软件中的有效焦距（Effective Focal Length，EFL）即是采用“小孔径法”追迹计算获得的。但“小孔径法”依托的数理定义难以指导开展实验测量，其原因在于入瞳上高度极小的小孔径近轴光线过于理想，是数学描述上存在而物理实践上难以操控的光线。通常采用“小像高法”实验测量光学系统焦距，即测量零视场旁极小视场角的旁轴光线对应的像高计算焦距，该方式在光学设计中亦可通过光线追迹计算实现，在光学设计软件中体现为畸变焦距（Distortion Focal Length，DFL）。尽管“小像高法”选定的是极小视场角的旁轴光线，但与“小孔径法”的焦距本征定义相比，“小像高法”测得的焦距中因有视场要素，仍不免耦合了成像畸变。如果以“小孔径法”作为焦距的设计描述，以“小像高法”作为焦距的测量描述，则存在着设计指标不是检验指标的逻辑矛盾。

光学系统设计时，一般通过在评价函数中追迹控制各采样视场主光线的实际像高与投影模型规定的理想像高的偏差量实现对畸变的优化校正。在光学系统实物加工完成后，采用对标准网格板成像的方式可以实现畸变的测量。但对于大视场的光学系统，比如视场角超过120°的广角镜头，网格板构建困难，通常采用精密测角法标定镜头的畸变，确立实际的物像映射关系［6-9］。

“小像高法”作为焦距测量的描述方式，与投影模型的定义高度吻合，是投影模型中视场角极小时的特殊情况。畸变是视场相关的参数，如果将焦距也变成视场相关的参数，则可以对其赋予“小像高法”的定义［10］。考虑到焦距和畸变共同描述了实际光学系统的物像映射关系，本文将焦距的内涵由零视场拓展至全视场，对非零视场也赋予焦距值，形成局部焦距（Local Focal Length，LFL）的概念。采用“小像高法”的定义方式对局部焦距进行赋值，可以描述各视场处，极小视场角增量光线对应的像高增量。继而，原本由传统焦距和畸变共同描述的物像映射关系，可以由局部焦距这一单一参量表征。局部焦距全面覆盖了轴上和轴外视场，解决了传统焦距“小像高法”测量描述中耦合畸变的问题。按照上述思路，可由理想投影模型推导光学设计时局部焦距的目标值，实际局部焦距与目标值的偏差也等价于畸变。另一方面，可以基于精密测角法的原理，按照“小像高法”测量局部焦距，实现设计描述和测量描述的统一。本文在广角镜头的设计中引入局部焦距，开展优化设计方法研究，旨在通过对全视场范围内局部焦距的追迹计算和优化控制，满足各类型复杂的物像映射关系。

1 局部焦距的定义

1.1 焦距的“小孔径法”和“小像高法”描述

光学系统焦距的本征定义如图1（a），是像方主面与像方焦点之间的距离。依照“小孔径法”，追迹平行于光轴、在入瞳上高度值h极小的近轴光线，获取其经光学系统与光轴的夹角U′计算焦距。

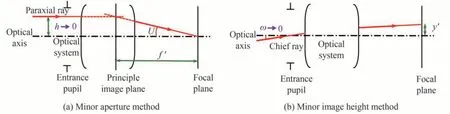
图1 焦距的追迹计算方法Fig. 1 Principles for focal length calculation utilizing ray tracing

焦距的“小像高法”定义方式如图1（b），追迹过入瞳中心、与光轴夹角ω极小的旁轴光线，获取其在像面（焦面）上的高度y′计算焦距。

在光学设计软件中，无论是平行于光轴、在入瞳上高度值h极小的近轴光线，还是过入瞳中心、与光轴夹角ω极小的旁轴光线，均可以通过设置合理的光瞳和视场采样，追迹满足上述要求的特征光线。

然而，由于实验采用的测量光束存在一定的口径，无限接近于光轴的细光路难以物理实现，导致准确测量会聚光线与光轴的夹角极其困难。相对而言，角度和像高的测量更具有物理实操的可行性，现有的焦距测量方法大多采用精密测角法。“小像高法”指引了焦距的实验测量，但轴外视场的像高中不可避免地耦合了畸变。因此，对于视场较大、畸变像差较为显著的光学系统，其有效焦距和畸变焦距通常不一样。在光学设计的过程中，设计时通常只关注有效焦距，忽略畸变焦距，造成设计指标和检验指标的不一致。

1.2 局部焦距的“小像高法”定义

将焦距的内涵从轴上视场拓展到轴外视场，则形成局部焦距的概念，局部焦距采用“小像高法”的定义方式全面覆盖了从轴上零视场到轴外边缘视场所有各视场角对应的焦距值。如图2 所示，假定在全视场范围内某个视场角θ的主光线在焦面上的像高为y′，追迹相对该视场角有极小视场角增量Δθ的主光线，获得对应的像高增量Δy′，则视场角θ时的局部焦距LFL 表示为

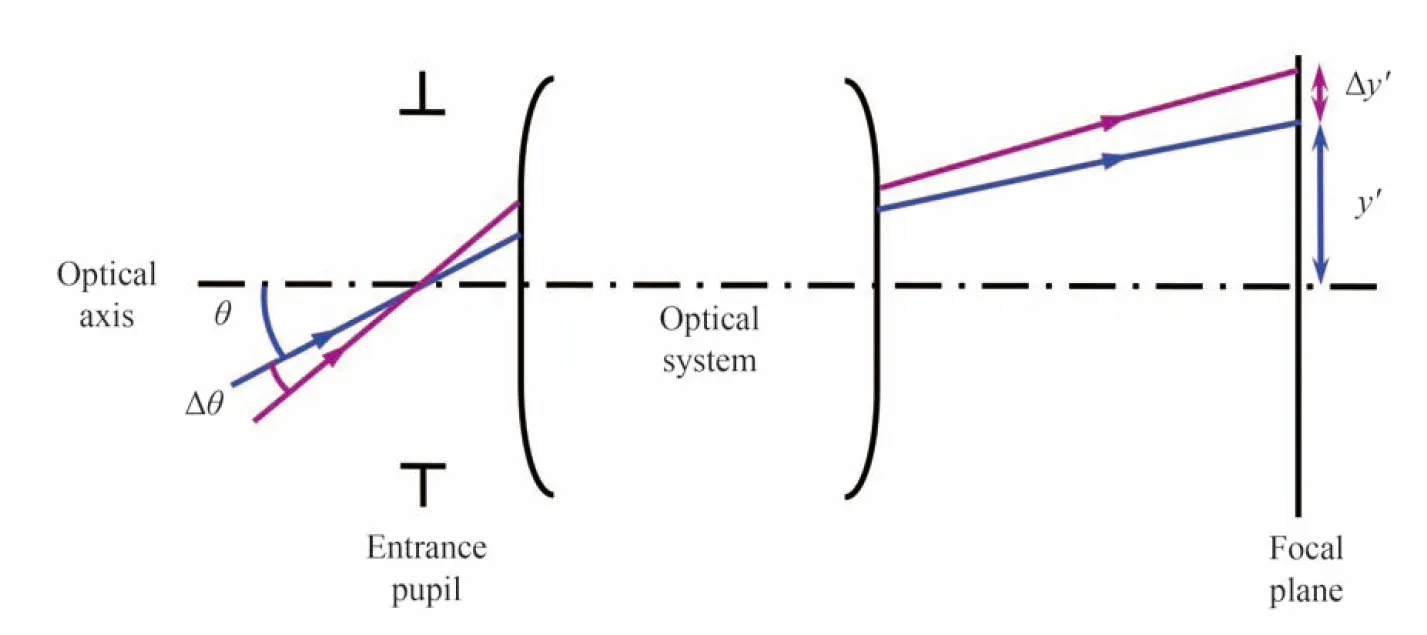
图2 局部焦距的定义Fig. 2 Definitions for local focal length.

上述的视场角增量Δθ按照径向方向增长，适用于旋转对称的光学系统。对于旋转非对称的光学系统，需要在子午和弧矢，甚至更复杂的方向引入视场角增量，计算多方向的局部焦距值。

1.3 投影模型的局部焦距

按照式（3）求解等线投影映射、等距投影映射、体视投影映射、等立体角投影映射、正交投影映射的局部焦距，将其表达式列入表1。等距投影模型的各视场局部焦距值相同。

表1 投影模型的局部焦距Table 1 Local focal length for projection models

2 广角镜头的设计

小视场光学系统的物像映射投影关系较为简单，而大视场光学系统的物方场景较为复杂，目标映射的需求也不尽相同。因此，本文研究将局部焦距的调控变换应用到广角镜头的设计中。

2.1 中央视场等线投影的160°鱼眼镜头

鱼眼镜头是一种典型的超广角光学系统，其结构特点是第一片透镜呈弯月型，可实现超广角入射光线的大倾角变化，其视场接近甚至超过180°。由于鱼眼镜头的视场较大，如果按照大多数成像系统常规采用的y'=f'tanθ等线投影模型，那么边缘视场的像高太大。因此，鱼眼镜头的设计通常满足y'=f'θ等距投影模型。

以靶面1/4 英寸（1 英寸=2.54 cm）的OV9281 型探测器作为成像接收器，其像素数为1 296×816，单个像素尺寸为3 μm×3 μm。首先设计一款全视场160°，F数为4.2，工作波长为可见光，满足y'=f'θ等距投影模型的鱼眼镜头，按照探测器靶面对角线长度并留有一定余量，设置像面为±2.25 mm，则其轴上焦距为1.61 mm。如表1，其各视场的局部焦距LFL 均为1.61 mm。光学设计时从轴上至边缘视场等间隔采样11 个视场角，不控制目标像高，而是按照“小像高法”追迹计算各采样视场的局部焦距值，实现焦距与投影模型同步优化控制的效果。优化设计的镜头结构如图3（a），采用6 片透镜，其中1 片塑料非球面，全视场点列图均方根半径达到衍射极限。如图4（a），全视场局部焦距与目标值的相对偏差≤0.5%，通过设计软件追迹计算，实际像高与y'=f'θ等距投影模型的偏离量≤0.3%。

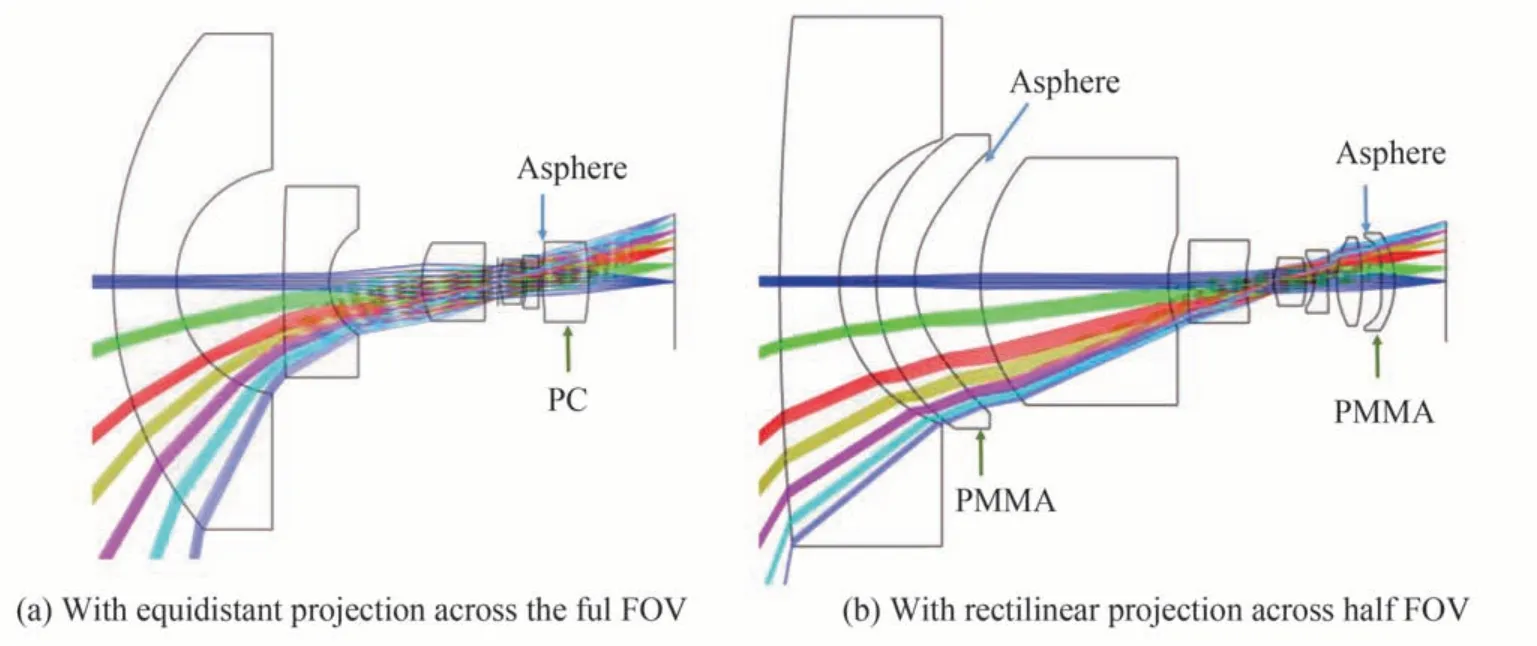
图3 采用局部焦距追迹计算优化的160°视场鱼眼镜头的光学设计结果Fig. 3 Optical layouts of fisheye lens with 160° FOVs utilizing LFL raytracing and controlling

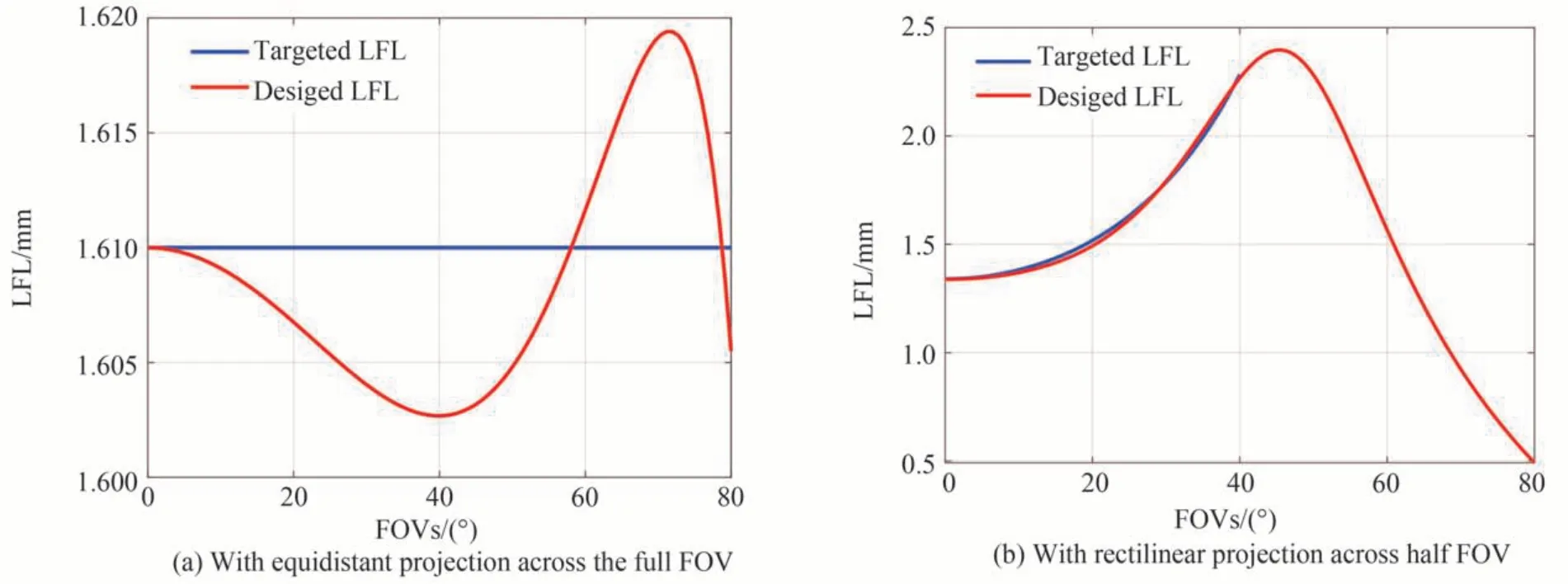
图4 160°视场鱼眼镜头的目标局部焦距值和设计局部焦距值曲线Fig. 4 Curves of targeted LFL and designed LFL for fisheye lens with 160°FOVs for the design configurations

上述等距投影鱼眼镜头对正方形网格的成像效果如图5（a），其各个局域均存在较为明显的网格畸变。但如前文所述，因为视场角较大，鱼眼镜头很难满足等线投影模型。继而，参考鱼眼中央凹的特征［11］，考虑对鱼眼镜头的中央视场设置为等线投影，对其边缘视场的物像映射关系不做限制。符合中央区域无畸变成像，边缘区域获得超大视场的鱼眼镜头成像目标。

图5 160°视场鱼眼镜头的网格畸变Fig. 5 Grid distortions for fisheye lens with 160° FOVs for the design configurations

仍采用OV9281 型探测器，设置±40°视场范围内满足等线投影，并占据50%的像面高度，根据上述要求可计算出轴上焦距为1.34 mm，局部焦距LFL 按照表1 中等线投影模型的公式计算，从中央到边缘各视场局部焦距渐变增加。光学设计时从轴上至50%视场等间隔采样6 个视场角，按照“小像高法”追迹计算并控制各采样视场的局部焦距值，对±40°～±80°的视场的局部焦距不做控制，仅控制80°视场的像高在探测器范围内。优化设计的镜头结构如图3（b），采用8 片透镜，其中2 片塑料非球面，全视场点列图均方根半径达到衍射极限。如图4（b），50%中央视场内局部焦距与目标值的相对偏差≤1.4%，通过设计软件追迹计算发现实际像高与等线投影模型的偏离量≤0.9%。对正方形网格的成像效果如图5（b），中央近60%的区域几乎无网格畸变，即局部焦距的调控方法工作效果较好。

2.2 曲面物体等分辨率映射的120°广角镜头

在2.1 节鱼眼镜头的设计中，物体被定义在无限远。但在大多数的成像场景中，物体在有限远，且物体也不一定为平面，常有曲面物体存在。例如，对地侦察相机的物面为地球表面，可看作对凸面的成像［12-13］。图6 为有限远曲面物体的物像关系。完整的成像关系可以由物面、入瞳、镜头、像面共同描述。图6 中曲面物体可以分为凸面（R＜0）和凹面（R＞0）两种，平面物体是R=∞的极端情况。图6 中，L表示物面与入瞳之间的间隔，平面物和曲面物的视场统一用视场角θ表示，α为视场角θ的曲面物的弧角，两者之间的关系可以表示为

图6 曲面物体的成像映射关系Fig. 6 Mapping relationships for curved object

式中，当物面为凹面，即R＞0 时，取正号；当物面为凸面，即R＜0 时，取负号。

有限共轭的平面物至平面像的成像关系通常满足y'=f'tanθ等线投影映射。类似地，当曲面物至平面像成像时，为了满足物像的相似性，其投影模型为曲面物的等弧长增量对应平面像的等像高增量。其中，R=L的曲面物体最为特殊的，它的投影模型恰好为等距投影。当将平面物体看成R=∞的曲面物体时，其等线映射则与等弧长映射等价。

对视场120°的广角镜头采用局部焦距追迹计算控制的方法开展曲面物体成像设计，工作波长为可见光，L为1 000 mm，F 数为2.8，轴上焦距设置为1 mm。选择R=800 mm，R=1 000 mm，R=1 200 mm 的凹面，R=-20 000 mm 的凸面，以及R=∞成像物面做设计比对，球面采用等弧长映射，平面采用等物高映射的成像关系。为了方便比对，每种结构均采用8 片透镜，其中可以使用塑料非球面，全视场点列图均方根半径优化至衍射极限。

对于各类型的成像物面，它们的最大视场角统一设置为60°。同时，在曲面物体上选择极小的旁轴弧角δα，其对应的视场角δθ可由式（4）获得。因为轴上视场的局部焦距为f0'=1 mm，则极小的旁轴弧角δα对应的目标像高可表示为

相应地，对于弧角为α的曲面物体，其对应的视场角θ可由式（4）获得。按照等弧长的物像映射关系，其对应的目标像高可以表示为

对于目标局部焦距的求解也可以参照以上方法。设置极小的弧角增量Δα，相应的追迹曲面物体上弧角分别为α和α+Δα的主光线，其对应的视场角θ和θ1可由式（4）获得，其对应的像高y'和y1'可由式（6）获得，则局部焦距可以表示为

根据上述等弧长物像映射关系公式，可计算出视场120°的广角镜头的目标像高和目标局部焦距值，其随视场角变化的目标映射曲线如图7。为了满足各种物面的等弧长映射目标，其对应的局部焦距的调控变换差距较大。

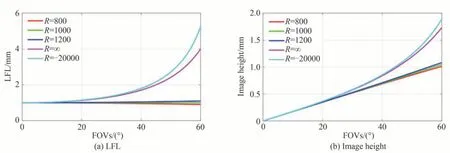
图7 120°广角镜头对曲面物体成像的等弧长目标映射曲线Fig. 7 Ideal mapping relationships for curved object utilizing wide angle lens with 120° FOVs

对4 个不同曲率半径的曲面物体和1 个平面物体，在0°～60°视场范围内等间隔采样11 个视场角，不控制目标像高，而是按照“小像高法”追迹计算各采样视场的局部焦距值，实现焦距与等弧长投影模型同步优化控制的效果。优化设计的镜头结构如图8 和9。在R=800 mm，R=1 000 mm，R=1 200 mm 的三个凹面成像的光学系统中均仅采用了1 片塑料非球面，全视场局部焦距与目标值的相对偏差≤0.2%，通过设计软件追迹计算，实际像高与等弧长映射的目标像高偏离量≤0.1%。在R=-20 000 mm 的凸面成像以及R=∞的平面成像的光学系统中，均采用了2 片塑料非球面，全视场局部焦距与目标值的相对偏差≤0.6%，通过设计软件追迹计算，实际像高与等弧长映射的目标像高偏离量≤0.21%。由此，可在120°视场范围内获得相同的物方分辨率。

图8 曲面物等弧长映射的120°广角镜头光学设计结果Fig. 8 Optical layouts of wide angel lens with 120° FOVs for curved object with equal arc length mapping

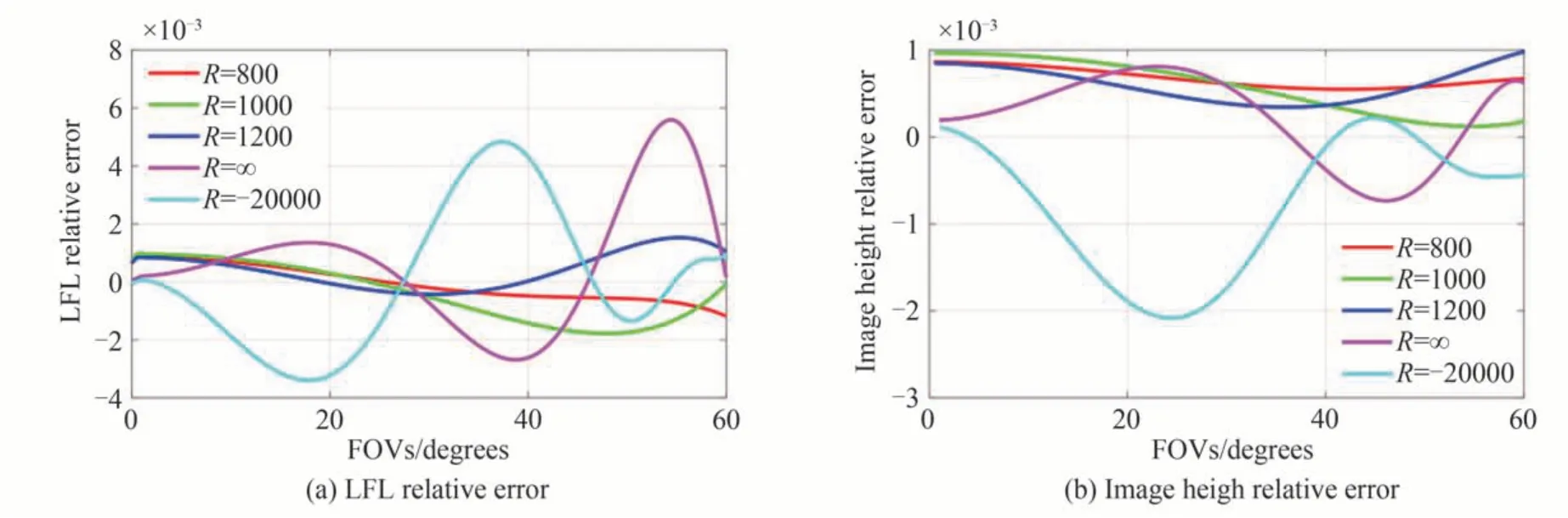
图9 曲面物等弧长映射的120°广角镜头的物像映射设计结果Fig. 9 Designed result of wide angel lens with 120° FOVs for curved object with equal arc length mapping

综合中央视场等线投影的160°鱼眼镜头和曲面物体等分辨率映射的120°广角镜头的设计效果可知：本文引入局部焦距替代传统焦距和畸变，结合常规的像质优化共同构建评价函数，获得了达衍射极限的像质和针对各类型复杂物像映射优于1%的成像畸变；通过对有限数量离散采样视场点局部焦距的追迹计算控制，能够在各类型复杂物像映射的场景下，优化获得满足目标的局部焦距，且全视场局部焦距呈连续分布。局部焦距表征了像高增量，将局部焦距做积分则为像高，本文通过对局部焦距的优化控制，获得了满足目标的像高。因此，局部焦距的追迹优化达到了系统焦距控制和物像映射控制的双重目标。另一方面，对于曲面物体的成像，难以构建物面网格测量成像畸变，但局部焦距采用“小像高法”定义，可以在像面放置靶标，通过精密测角法测量局部焦距值。因此，通过局部焦距的引入，达到了算测融合的效果。

3 结论

本文提出了局部焦距的概念，将焦距的内涵由零视场拓展至全视场，用来表征光学系统各视场处极小视场角增量光线对应的像高增量。并对其赋予了“小像高法”定义，使得焦距的定义方式和测量方式相吻合，设计参数和参量参数一致。应用对局部焦距的追迹计算，可以实现系统焦距和成像畸变的优化控制。据此设计了针对无限远目标成像，全视场角160°，50%中央视场满足f-tanθ等线投影的鱼眼镜头，以及针对有限远曲面物体成像，120°全视场范围物方分辨率相同的广角镜头。局部焦距在复杂物像映射场景光学系统的设计中具有较好的应用前景，且具有算测融合的显著优势。