修正磁化模型的多组分铁磁性颗粒运动研究1)

陈巨辉 安 然 舒崚峰 李 丹 刘晓刚 毛 颖 陈纪元 高浩铭 吕文生 孟凡奇

* (哈尔滨理工大学机械动力工程学院,哈尔滨 150080)

† (中国电建集团华东勘测设计研究院有限公司,杭州 311122)

** (中国航发哈尔滨东安发动机有限公司,哈尔滨 150066)

引言

铁磁性颗粒(简称“磁性颗粒”)在磁场中会自发地进行磁化,其被广泛地运用于靶向给药[1-2]、磁流变液[3-5]、磁性分选[6-9]、磁性新材料[10-11]和磁流化床[12-14]等领域中.常规的多相流动过程中产生的混合不均、沟流、节涌和分层等不良现象[15],可以通过添加外部磁场的方法对颗粒运动进行干预,对磁性颗粒流化过程中产生的不良现象加以改善与控制,减少颗粒运动中的不良现象,提高颗粒循环的运行效率,降低颗粒控制的运行成本[16].

磁性颗粒在磁场中受到磁场力与磁化力的共同作用,其中磁化力为国内外学者的研究重点.Rosensweig[17]对于单个球形磁性颗粒在磁场中受到的磁场力进行了推导与实验,结果表明,球形磁性颗粒在非均匀磁场中受到力的作用,该作用的方向与磁场梯度方向一致,其大小与磁场强度梯度、颗粒磁化率和颗粒体积成正比,进一步定量得到Rosensweig 磁场力公式,该计算磁场力模型具有较高的精度.

铁磁性颗粒在施加外磁场后可认为瞬间完成磁化过程,由于颗粒在磁化后具有极性,因此成对的铁磁性颗粒在磁场中会相互吸引或者排斥,最终形成聚链.Pinto-Espinoza[18]对于铁磁性颗粒在磁场中的运动进行了理论推导和模拟研究,其假定完全相同的两个颗粒,在垂直方向均匀外磁场的条件下,两个理想偶极铁磁性颗粒之间,施加的外磁场与铁磁性颗粒磁场叠加,结合磁场势能公式,推导提出了P-E磁化公式.为整个铁磁性颗粒模拟研究奠定了基础,但由于其采用均匀垂直磁场并未考虑磁感应强度梯度和磁场方向对于颗粒的作用,因此该模型具有一定的局限性.Hao 等[19]运用P-E 磁化模型与离散模型相结合,研究鼓泡流化床中添加垂直方向二维梯度磁场的运动状态,分析了不同磁感应强度下的铁磁性颗粒的速度与浓度变化.Ke 等[20]运用P-E 磁化模型与离散模型相结合,研究添加二维外部垂直恒定磁场计算域,模拟流体中磁性粒子的运动,得出结论,磁场的方向和磁性粒子的相对位置决定了相互作用力是吸引还是排斥,随着距离的增加,磁力迅速减小;当施加外部垂直恒定磁场时,磁场中的颗粒会发生链式聚集,铁磁性颗粒形成链状结构.

磁场流化床的众多优势使其在工业生产领域包括物料分离、颗粒筛选及改善黏性颗粒流化效果等方面承担了重要的作用[21-22].对于施加外磁场的颗粒多相流运动,主要研究磁性颗粒在磁流化床内的运动状态.Valverde 等[23]通过采取将气流与施加的外部磁场进行模拟耦合,研究磁场辅助下的颗粒流化状态,结果表明,施加的磁场使得颗粒与颗粒间产生力的作用,沿着磁场方向形成链状结构,颗粒成链长度与磁场强度、粒子磁化率、颗粒大小和颗粒密度有关,并提出了考虑形成磁链长度的Richardson-Zaki 方程.Zhu 等[24]针对具有可磁化和不可磁化颗粒的流化床,建立了一种基于快速测量相应沉降床内磁导率的新方法.避免了从沉降床中取样颗粒和随后分离两种类型的颗粒,从而消除了这两个步骤中所关注的许多问题,并且更加高效.杨慧等[25]研究掺杂铁粉的SiO2颗粒在磁流化床的运动,探究了磁场强度对床内气含率和局部压力波动均方根的影响,结果表明,随着床内磁场强度的增加,局部气含率和平均气含率均有所增大;当磁场强度一定时,颗粒粒径越大,局部气含率和平均气含率均增大;当磁场强度和床高增加时,床内压力波动升高.刘金平[26]研究纳米级铁磁性颗粒在微小磁流化床内的运动,模拟了纳米铁磁性颗粒在不同的床径、气速、配风和磁场强度下的运动,结果表明,在内径20 mm的微小流化床中,施加的外磁场可以抑制纳米颗粒产生的沟流现象,帮助颗粒维持稳定流动状态.Chen等[27]通过计算颗粒流体力学,研究了鼓泡床密相区颗粒的混合扩散对炉内反应速率的影响.Song 等[28]采用双流体模型结合多组分传质模型和气泡中尺度阻力模型来揭示活性颗粒的传质特性.Ganzha 等[29]对不同粒径、料床高度的铁磁性颗粒进行鼓泡流化实验,结果表明,当施加磁场的磁感应强度足够大时,观测到床内产生显著的磁场,该磁场影响施加的外部磁场,导致外磁场发生变形,铁磁性颗粒之间产生明显的作用力,并出现了成链团聚现象.Jovanovic等[30]在施加垂直方向梯度磁场的条件下,对于铁磁性颗粒的流化过程进行模拟,结果表明,添加垂直含梯度磁场,由于产生的磁场力与颗粒所受重力相互抵消,可以实现在微重力环境下的颗粒运动,并且磁力在阻止铁磁性颗粒在微重力条件下从床中逸出起着主要作用.

综上所述,学者们对铁磁粒子运动的研究多停留在垂直磁场和水平磁场上.本文提出一种改进的P-E 磁化模型,将适用范围从垂直磁场扩大到任意方向,能够计算空间中任意磁场方向下颗粒所受到磁化力,使得研究任意磁场方向对于磁性颗粒运动的影响成为可能.基于改进的P-E 磁化模型,采用有限体积法-离散单元法(finite volume method-discrete element method,FVM-DEM)模拟,研究了多组分颗粒在磁场中的运动,分析了不同磁场方向和不同配比对多组分颗粒聚链的影响.仿真结果为多组分铁磁粒子在磁场中的运动提供了理论依据和数据支持.为进一步研究铁磁性颗粒在不同磁场环境中的运动提供了一定的思路.

1 数学模型

1.1 FVM-DEM 模型

气相采用有限体积法,通过质量守恒方程和动量守恒方程描述.质量守恒方程

动量守恒方程

式中,εg为气相体积分数,Kgp为单位体积网格内固相与气相的相间交换系数.

固相采用离散单元法,通过牛顿定律得到颗粒的运动方程与转动方程.颗粒运动方程

颗粒转动方程

其中产生的曳力采用Spherical 曳力模型进行描述,其表达式如下

式中,C为曳力系数,a1,a2和a3为根据不同Re的定值常数.其中液固相间耦合需计算由于曳力作用产生的动量交换源项,其表达式如下

颗粒运动发生碰撞受到接触力Fc作用,采用Hertz-Mindlin[31-32]接触模型计算颗粒接触力

式中,Fr为径向接触力,Frd为径向阻尼力,Ft为切向接触力,Ftd为切向阻尼力,E*为当量杨氏模量,R*为当量弹性模量,δr为径向重叠量,δt为法向重叠量,m*为当量质量,vn、vt为相对速度的法向、切向分量,α0为修正恢复系数,Dn和Dt为法向和切向刚度.将作用力与阻尼力矢量叠加进而计算出颗粒碰撞合力如下

式中,r为径向方向向量,t为切向方向向量.

颗粒所受磁场力Fme与磁场方向保持一致,磁化力Fmi可分解为径向磁化力Fmi,r和切向磁化力Fmi,φ.因此颗粒所受总磁力表达式如下

式中,Vp为颗粒体积,μ0为真空磁导率,χp为磁化率,H为磁感应强度.

1.2 修正P-E 模型

本文采用相对坐标系转换方法,在相对坐标系中采用传统P-E 模型,从而实现P-E 模型适用于任意方向磁场.基于常规坐标系xoy,以计算颗粒为圆心,以磁场方向为y'正方向,x'正方向为y'顺时针旋转90°方向,建立相对参考系x'oy',颗粒对相对坐标系如图1 所示.

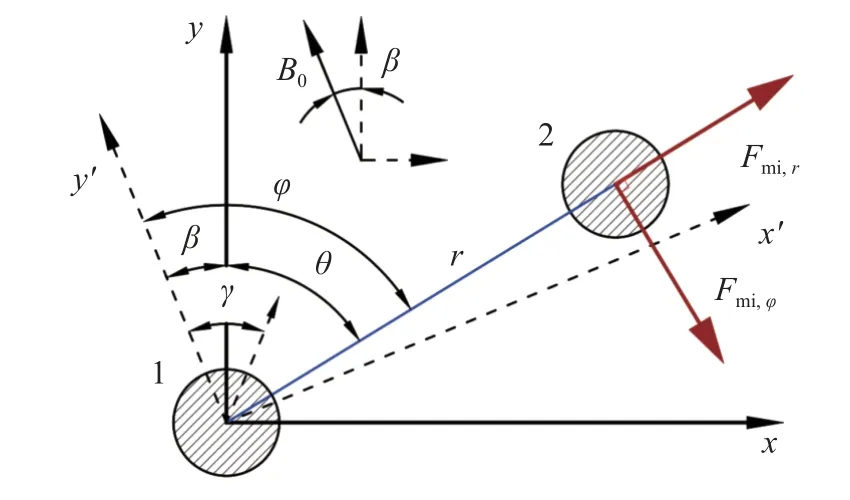
图1 颗粒对相对坐标系Fig.1 Relative coordinate system of particle pairs

图1 中,β为磁场偏角,γ为偶极角,B0为磁通量密度.由于施加外加磁场方向β为任意方向,可以通过方向向量方式表示磁化偏角和磁偶极矩关系

同理可以通过单位向量表示颗粒中心连线方向

通过相对参考系计算颗粒对产生的磁偶极矩为

其中空间一点磁偶对产生的磁场大小计算公式如下

结合式(16)、式(17)和式(20),通过三角函数向量计算并整理得到

假设两种颗粒种类大小完全相同,因此m=m1=m2,并代入式(18)得到磁偶极矩表达式

由于选取相同颗粒,通过式(16)与式(22)方向向量系数对照,得到二元一次方程组

通过求解方程组,可解出相对参考系中γ偶极角与m磁偶极矩

因此就可以通过势能对径向和角向进行微分,计算出径向磁力和角磁力

式中U为偶极子之间的势能.

进而计算径向磁化力与切向磁化力大小

式(29)和式(30)即为修正P-E 磁化模型.

2 模拟条件

2.1 仿真模型

模拟结构采用伪二维的几何结构,该结构长0.01 m、宽0.001 m 和高0.04 m.模拟过程采用FVM-DEM 耦合模拟流程,连续相采用有限体积法,离散单元法追踪颗粒并根据牛顿定律计算求解.采用ICEM 软件对流体域建模并进行网格划分,几何模型导入EDEM 软件,将修正P-E 磁化模型编写为动态链接库文件导入,并采用DEM 方法计算离散颗粒运动参数;网格导入FLUENT 软件,采用FVM 方法计算流体域参数,通过自定义函数实现FLUENTEDEM 双平台耦合仿真.将EDEM 时间步长设置为1×10-6s,Fluent 时间步长设置为2×10-5s,两者的耦合时间步长差为20 倍,节省了计算机资源,提高仿真精度,保持流程时间同步,输出参数时间同步.

2.2 网格无关性验证

参考颗粒总动能选取网格尺寸,选取的网格尺寸能够保持系统内较低的总动能,即可认为网格已经符合要求,其中网格无关性检验结果见表1 所示.

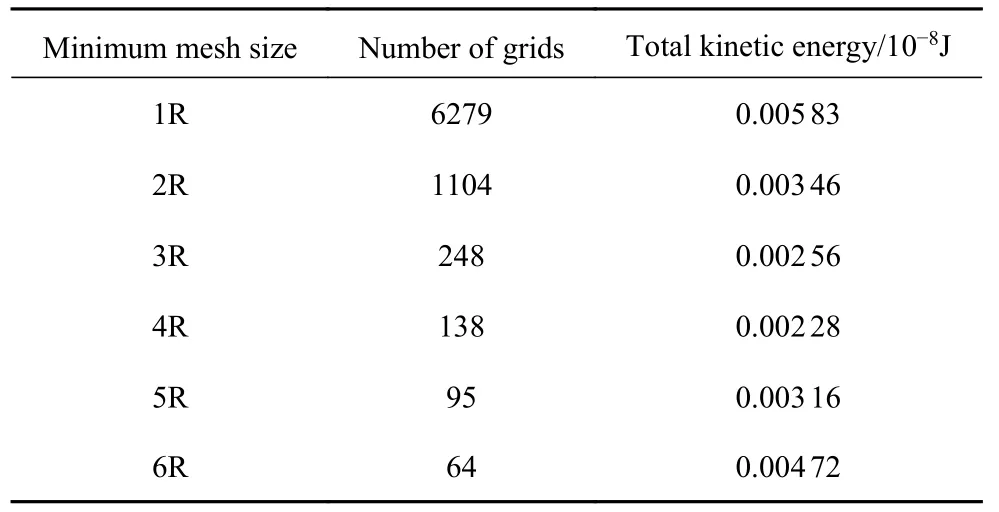
表1 网格无关性检验表Table 1 Grid independence test table

由表1 可知,采用4R 至3R 所得到的模拟结果较为稳定,对于离散颗粒模拟过程,网格的主要作用是用于颗粒的检索,过小的网格不利于对颗粒的追踪,易产生较大误差.基于求解器的计算稳定性、曳力计算的精度等问题,一般要求流体域网格尺寸大于颗粒至少3 倍.因此综合多方面的因素考虑选取3R 的网格尺寸,网格数量为248,该网格较为精细且同时满足双平台软件使用的需求.

2.3 模型验证

修正P-E 磁化模型的验证,选取Pinto-Espinoza[18]的实验数据和Ke 等[20]所使用P-E 磁化模型模拟数据作为对比数据.采用FVM-DEM 耦合模拟方法对双颗粒运动进行模拟验证,模拟铁磁性颗粒在不同条件下所受到的磁化力对运动的影响.模拟参数如表2 所示.

表2 模拟参数Table 2 Analog parameters

选取单个铁磁性颗粒作为研究对象,模拟当施加垂直方向磁场时,另一个铁磁性颗粒以固定的颗粒间距围绕其转动(颗粒对偏角θ),记录颗粒所产生的磁化力.选取对应3 种工况,研究铁磁性颗粒所受磁化力,模拟工况如表3 所示.

表3 模拟工况表Table 3 Simulated working condition table

在不同的工况条件下,分别进行模拟并记录观测颗粒所受到的磁化力的作用效果,将模拟结果进行统计并得到磁化力变化图如图2 所示.

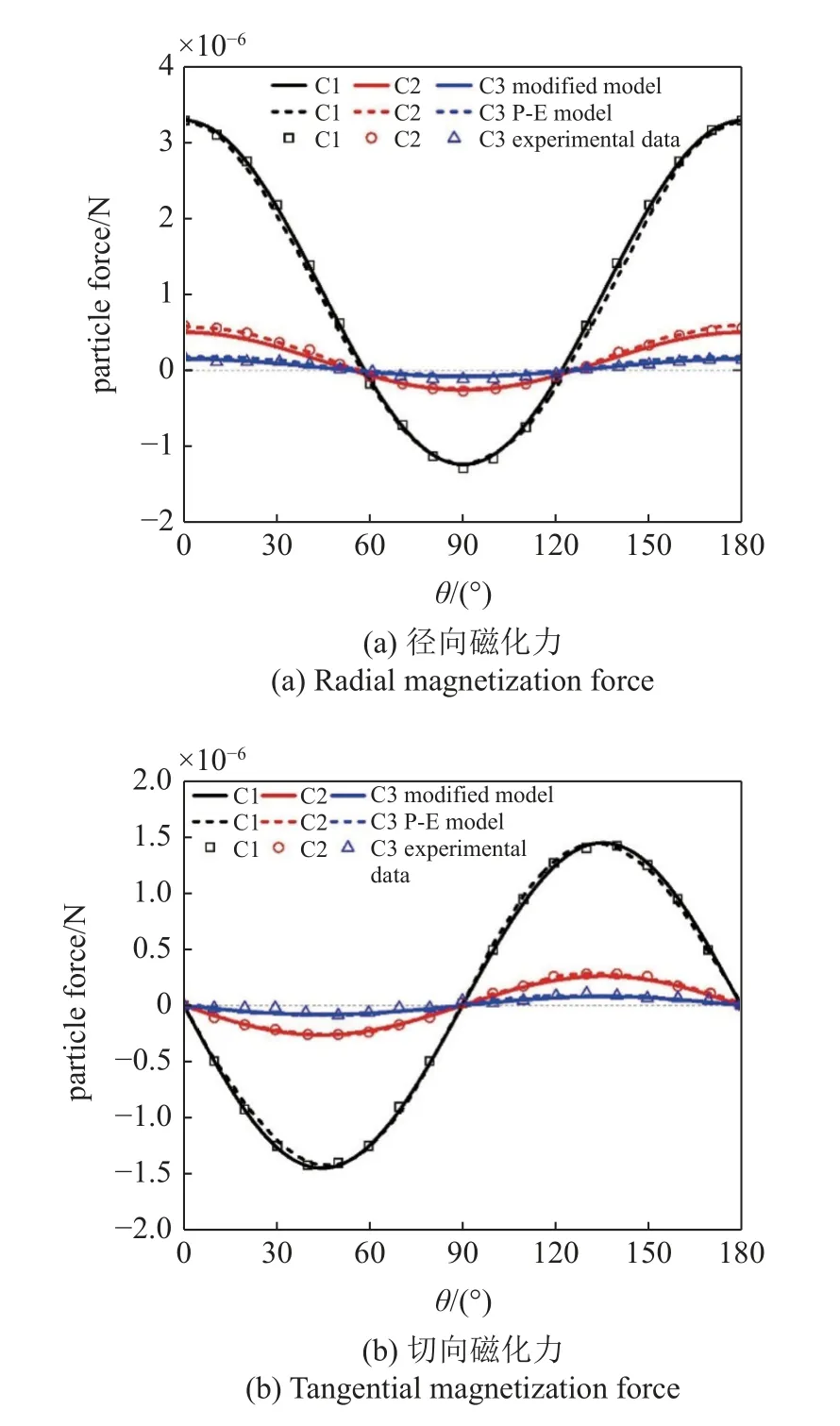
图2 磁化力变化图Fig.2 Magnetization force change diagram

由图2(a) 和图2(b) 可知,铁磁性颗粒在B0=0.02 T 的条件下,不同θ偏角时颗粒所受磁化力.修正P-E 模型的磁化力的计算结果与实验数据几乎保持一致,偏差保证在5%以内,且比原模型计算得到的磁化力更贴近实验数据,因此该模型具有可靠性.

为保证铁磁性颗粒在磁场环境下的充分运动,通过检测颗粒总动能可以确定颗粒是否达到稳定状态,选取工况C1 颗粒总动能变化图如图3 所示.

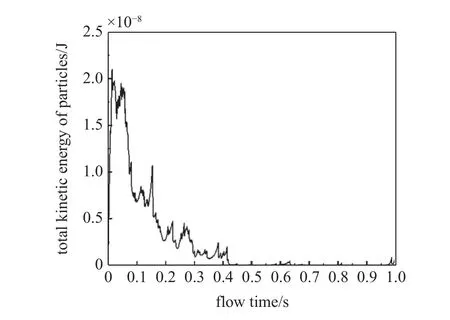
图3 C1 总动能Fig.3 C1 total kinetic energy

由图3 可知,总动能初始时刻突然增高,随流动时间而逐渐降低,该过程中伴随部分尖峰.由于磁场将颗粒磁化,颗粒受到的磁化力大小与方向,和颗粒对的空间位置有着密切的相关,尽管部分颗粒达到稳定状态,但细微的变化都会导致颗粒的运动变化,因此当系统内总动能降低到最高动能的5%时,即可认为系统已经达到稳定状态.

对于研究不同磁场方向及不同配比条件下的铁磁性颗粒与惰性颗粒在磁场中的运动特性,模拟的各项参数见表4.

表4 模拟参数表Table 4 Analog parameter table

铁磁性颗粒与惰性颗粒的掺混,采用不同组分配比时,会影响颗粒在磁场中的运动状态,因此引入铁磁性颗粒配比变量,公式如下

其中,Nm为铁磁性颗粒数量,NA为注入颗粒数量.选取3 种不同铁磁性颗粒占比和磁场方向设计模拟工况,选取磁感应强度B0=0.02 T,其中模拟工况见表5.

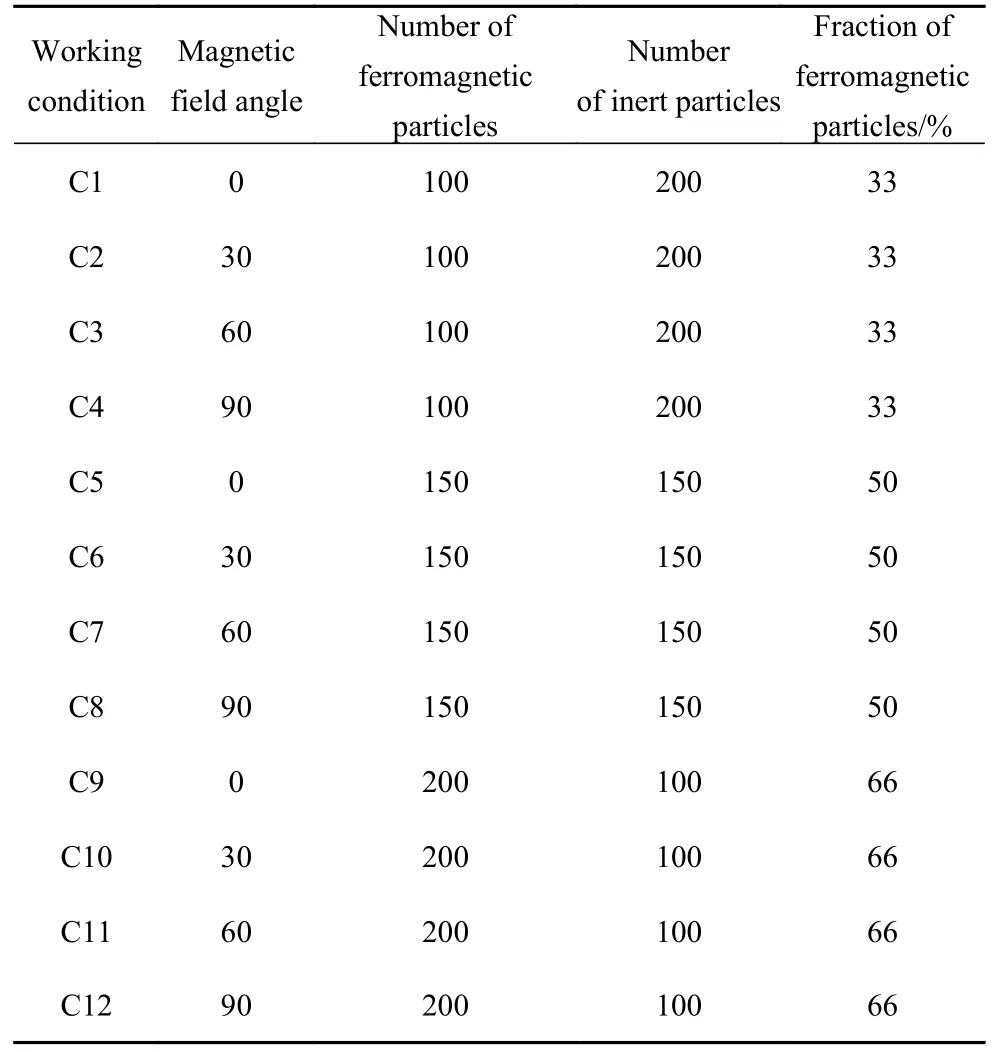
表5 模拟工况表Table 5 Simulated working condition table

3 结果与分析

3.1 磁场方向对多组分颗粒运动模拟与分析

基于各工况的模拟结果,选取模拟流动时长为1 s,由于磁场中惰性颗粒的存在,系统无法快速达到稳定状态,提取0,0.2,0.4,0.6,0.8 和1 s 时刻的颗粒分布图.为了方便区分铁磁性颗粒与惰性颗粒,铁磁性颗粒在分布图中为蓝,惰性颗粒为红.当铁磁性颗粒与惰性颗粒占比为1:1(K=50%)时,系统内各时刻颗粒分布图如图4 所示.

由图4(a)和图4(d)可知,多组分颗粒施加垂直或水平方向的磁场,惰性颗粒未形成聚链,铁磁性颗粒形成沿磁场方向的部分聚链,垂直磁场方向保持排斥.但由于惰性颗粒与铁磁性颗粒的碰撞,使得铁磁性颗粒的成链速度大幅下降,并难以形成较长的聚链.

由图4(b)和图4(c)可知,多组分颗粒施加β=30°或β=60°的磁场,仅铁磁性颗粒形成沿磁场方向的聚链,垂直磁场方向上相互排斥,其中铁磁性颗粒夹带着部分惰性颗粒沿着磁场方向发生偏转,其偏转角度与磁场偏角相等,铁磁性颗粒形成含有一定偏角的聚链状态,需要更长的流动时间,且颗粒成链的长度有所下降.

可以发现,惰性颗粒并不会在磁场作用下形成聚链,但由于铁磁性颗粒与惰性颗粒的碰撞,使得部分惰性颗粒夹杂于铁磁性颗粒聚链之间的间隙中.得出结论,多组分颗粒在不同磁场中的运动,由于惰性颗粒的存在,使得铁磁性颗粒沿着磁场的方向成链速度有所下降,形成的聚链长度有所下降,部分惰性颗粒夹杂在颗粒聚链中.

其中选取各工况1 s 时刻,提取铁磁性颗粒和惰性颗粒的速度矢量,得到系统内颗粒速度矢量图如图5 所示.

图5 1 s 时刻颗粒速度矢量图Fig.5 Particle velocity vector diagram at 1 s

由图5 可知,工况C5 铁磁性颗粒与部分惰性颗粒的速度矢量指向于分层中心;工况C6 和C7 铁磁性颗粒与部分惰性颗粒,左侧速度矢量垂直向上,右侧速度矢量垂直向下,局部颗粒速度矢量形成环形,铁磁性颗粒与部分惰性颗粒沿着顺时针方向逐渐形成沿磁场方向的偏转;工况C8 局部颗粒速度矢量形成环形.得出结论,多组分颗粒系统下,部分惰性颗粒会被铁磁性颗粒包裹与夹带,处于铁磁性颗粒聚链的间隙中,其余惰性颗粒游离在聚链外.

进一步提取以上4 种工况不同时刻的总动能,得到颗粒总动能变化曲线如图6 所示.

图6 总动能变化曲线Fig.6 Total kinetic energy change curve

由图6 可知,当K=50%时,4 种工况所具有的初始能量几乎相等,工况C5 与C8 采用垂直与水平方向磁场,其总动能曲线下降段的斜率,即颗粒成链速度相比含磁场倾角的工况C6 与C7 高,并且曲线下降速度更快,系统总动能更早趋近于0,更为迅速地达到稳定状态.得出结论,当颗粒配比为1:1 时,施加不同方向的磁场,铁磁性颗粒初始状态下能量不变,且当施加水平与竖直方向磁场,多组分颗粒系统达到稳定速度最快.

3.2 铁磁性颗粒配比对颗粒运动模拟与分析

采用3 种不同铁磁性颗粒与惰性颗粒的配比,分别研究1:2,1:1 和2:1 的颗粒配比(即K分别为33%,50%和66%)下,颗粒在不同磁场中的运动与分布,选取4 组对照工况,提取其1 s 时刻的颗粒分布图.组合相同磁场偏角的工况,其1 s 时颗粒分布图如图7 所示.

图7 1 s 时刻颗粒分布图Fig.7 Particle distribution map at 1 s

由图7(a)可知,工况C1,C5 和C9 采用垂直磁场,铁磁性颗粒占比逐渐升高.各工况均出现了颗粒聚链现象,C1 形成较短聚链,C5 聚链数量增多且开始出现分层现象,C9 形成了较长聚链且出现明显分层现象.

由图7(b)和图7(c)可知,工况C2,C6 和C10 采用β=30°倾角磁场,工况C3,C7 和C11 采用β=60°倾角磁场,随着铁磁性颗粒占比逐渐升高,铁磁性颗粒沿磁场方向的聚链增多,并形成长链,而且铁磁性颗粒对惰性颗粒的束缚能力逐渐增强,更为紧密地将惰性颗粒包裹在铁磁性颗粒的聚链中.

由图7(d)可知,工况C4,C8 和C12 采用水平磁场.分析不同配比下铁磁性颗粒的聚链变化,得出同样结论,随着铁磁性颗粒占比增加,聚链数量与成链长度同样有所增加,铁磁性颗粒对惰性颗粒的束缚能力逐渐增强,将惰性颗粒更紧密地包裹在颗粒聚链中.

提取以上12 种工况不同时刻的总动能,得到颗粒总动能变化曲线如图8 所示.

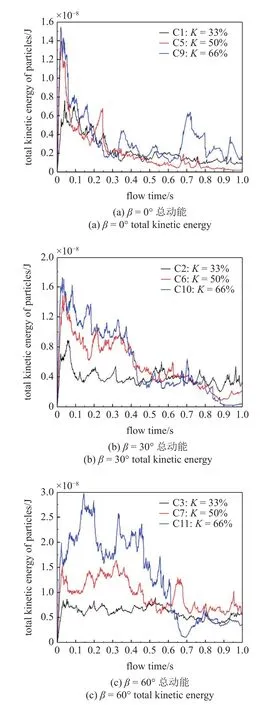
图8 总动能变化曲线Fig.8 Total kinetic energy change curve

由图8 对各组内部数据进行对比,能够直观得到结论,当铁磁性颗粒占比越高,颗粒初始状态所具有的能量均有所增加.观察曲线的变化,通过总动能下降过程中的斜率,进而判断成链速度达到稳定快慢,得到结论,铁磁性颗粒占比越高,多组分颗粒系统越容易达到稳定,颗粒的成链速度也就越快.且由图8(b)和图8(c)可知,含有磁场偏角的多组分颗粒,总动能变化剧烈,运动中较难达到稳定状态.

认为总动能降低为最高动能5% 则达到稳定,经过整理得到稳定时刻直方图如图9 所示.

图9 各工况稳定时刻直方图Fig.9 Histogram of stable time of each working condition

图9 中工况C1,C2,C3,C4,C6,C7 和C9 未在1 s 内达到稳定状态,系统仍具有波动.对比图中工况C4,C8 和C12 数据可知,当采用水平方向磁场时,铁磁性颗粒占比越大,稳定所需时间从1 s 以上缩短至0.2 s,颗粒达到稳定状态的速度显著增快.

4 结论

本文采用FVM-DEM 耦合模拟方法,结合修正P-E 模型,模拟研究铁磁性颗粒在惰性颗粒掺混的条件下,不同磁场方向与不同组分配比对铁磁性颗粒运动的影响,通过模拟得到各个工况的数据参数,整理得到颗粒分布图、颗粒速度矢量图和颗粒总能量变化图,对模拟结果进行分析,总结了多组分颗粒在不同工况下的运动规律.为铁磁性颗粒在不同磁场中的运动,提供了理论模型与模拟参考,得出主要结论如下.

(1) 在多组分颗粒系统中,施加不同倾角的磁场时,铁磁性颗粒仍会沿磁场方向形成聚链,但其颗粒聚链长度与成链速度相比垂直磁场有所下降,且部分惰性颗粒会被铁磁性颗粒包裹与夹带,处于铁磁性颗粒聚链的间隙中;铁磁性颗粒占比为1:1 时,铁磁性颗粒具有的初始能量不受磁场方向的影响,且当施加水平与竖直方向磁场时,多组分颗粒系统达到稳定速度最快.

(2) 在多组分颗粒系统中,随着铁磁性颗粒占比升高,铁磁性颗粒具有的初始能量将有所升高、聚链数量与成链长度将有所增加、铁磁性颗粒对惰性颗粒的束缚能力逐渐增强;当施加含有倾角的磁场时,随着铁磁性颗粒占比升高,铁磁性颗粒达到稳定状态需要的时间逐渐缩短.

(3) 在多组分颗粒系统中,施加水平磁场时,可以通过增大铁磁性颗粒占比有效提升稳定速度,使系统更快趋于稳定;但对于施加磁场偏角的工况,较难通过改变铁磁性颗粒占比缩短稳定所需时间.