时变载荷作用下饱和黏土地基的流变固结特性研究1)
王立安 余云燕 孙建忠 陈 辉
* (兰州交通大学铁道技术学院,兰州 730070)
† (兰州交通大学土木工程学院,兰州 730070)
引言
饱和黏土地基的固结沉降是影响工程建设和结构安全服役的重要问题[1-2].传统理论中,将土体的时间效应和长期变形归因于渗流固结,即超静孔隙水压力消散,外力完全转化为土骨架的有效应力[3-4].然而,这一观点与工程测试和实验模拟结果并不完全一致[5-7].尤其对于渗透性很差的饱和黏土,因孔隙水很难渗透,导致孔压难以消散,所以饱和黏土地基的固结沉降主要取决于流变.
天然土体具有固-流两相组成和骨架孔隙结构,对于黏性土,其固体骨架不是简单的弹性材料,而是介于牛顿流体和弹性固体之间的黏弹性材料.在载荷作用下,土颗粒的重新排列和骨架错位会对应力–应变关系产生时间效应,称为流变性[8-12].大量实验表明,饱和黏土在固结过程中,主固结阶段和次固结阶段都伴有流变现象,即孔隙压力消散和流变行为是耦合发生的.为了描述土骨架的流变效应,Taylor等[13]最先使用Kelvin 线性流变模型研究了饱和黏土的流变固结.Tan[14]利用Maxwell 模型考虑黏土的二次时间效应,并提出黏弹性固结理论.基于类似研究方法,Abousleiman 等[15]、Xie 等[16]、Liu 等[17]和Ai 等[18]采用整数阶Merchant 模型,研究了不同载荷形式及边界条件下饱和黏土的固结特性.然而,近些年学者们通过对比实验结果,逐步发现传统整数阶流变模型在模拟黏土固结时不能满足精度要求,需引入更多拟合参数才能实现有效模拟[19-20].进一步研究成果表明,Blair[21]和Gerasimov[22]提出的分数阶流变模型能够反映土骨架的无流动黏性,对黏性土具有更好的适用性[23-24].最新报道的文献中,Ai 等[25]利用分数阶Merchant 模型研究了多层各向异性饱和黏土的轴对称固结.Wang[26]考虑温度效应研究了流变性饱和黏土的固结特性.此外,Cheng 等[27]提出了超固结饱和黏土的分数阶双表面塑性模型.能够看出,上述关于流变性饱和土固结特性的研究都只针对于恒定载荷,未考虑载荷随时间的变化.实际工程中,地基土受到的载荷通常是随时间变化的,如建筑物从开始建设到最终建成,作用于地基土的压力逐渐增大而后保持恒定,该过程中地基土受到的压力可视为斜坡载荷;再如施工中的临时设施,先被建成而后拆除(三角形载荷);以及地基土的预压固结,先逐级加载而后保持恒载,最后卸载,该过程可视为梯形载荷.尽管Cai 等[28]和耿雪玉等[29]利用时域函数考虑载荷随时间的变化,对饱和土地基的固结问题做了研究,但采用的土体模型未反映流变效应.
为探索载荷变化和土骨架流变耦合作用下饱和黏土地基的固结特性,本文基于Biot 固结理论,利用分数阶Kelvin 流变模型描述土骨架应力-应变关系,引入斜坡、三角形和梯形3 种时变载荷的时空域解析函数,构建饱和黏土地基的三维轴对称固结模型.采用Hankel–Laplace 联合变换推导控制方程的变换域解析解,然后通过数值反演获得时空域解.最后,通过算例分析,讨论了饱和黏土地基的固结特性及其物理参数的影响.
1 力学模型
1.1 分数阶Kelvin 模型
经典Kelvin 模型是由一个弹簧元件K和一个Newton 黏壶N并联而成,如图1.将经典Kelvin 模型中的Newton 黏壶替换为Abel 黏壶[30],则得到分数阶Kelvin 流变模型,其本构关系描述为
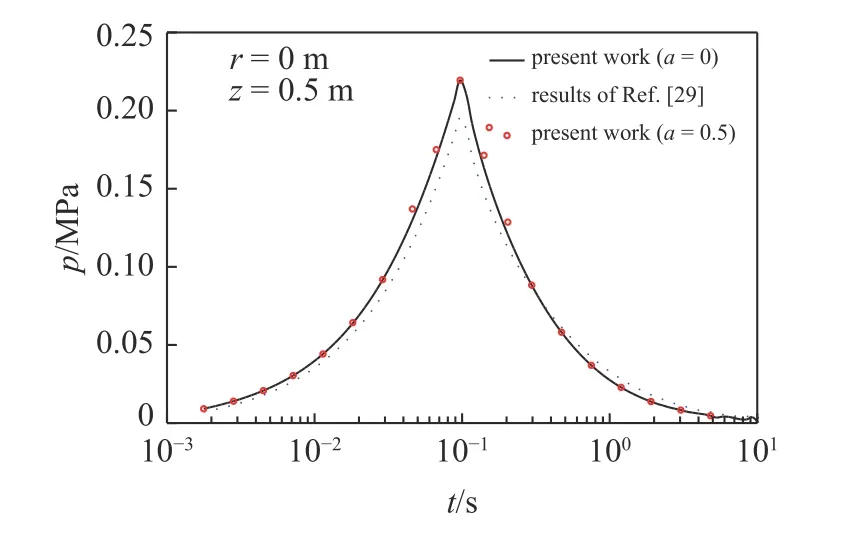
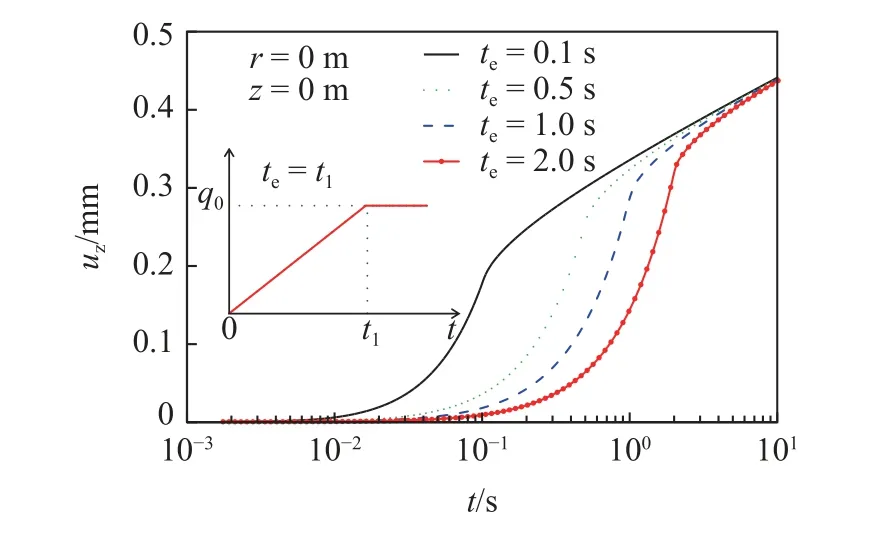
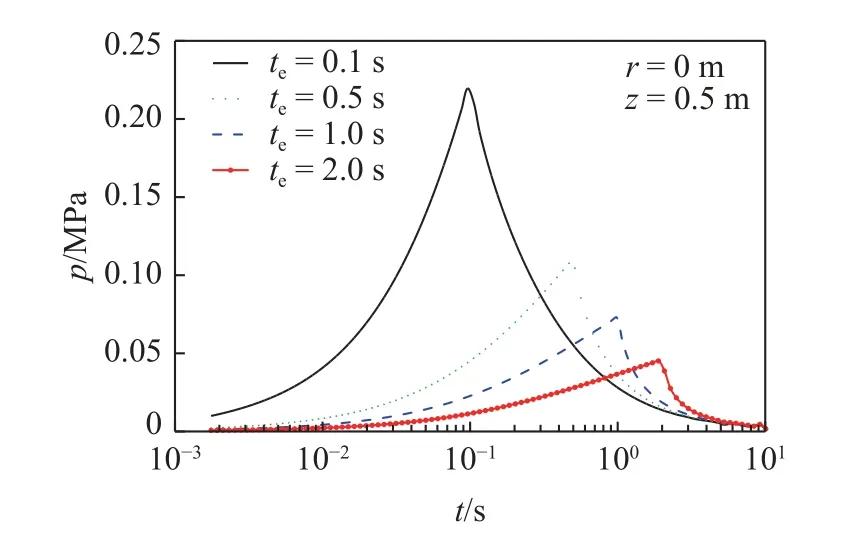
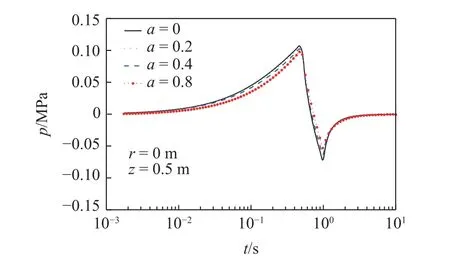
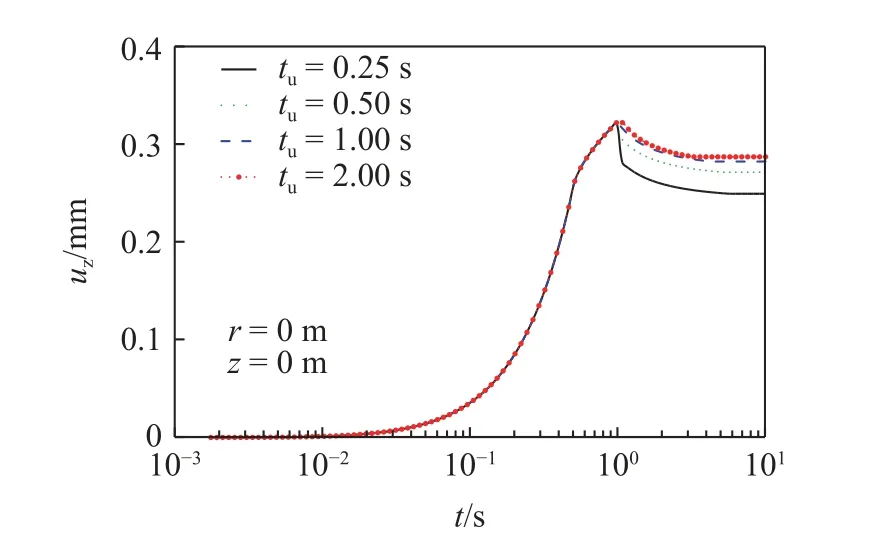
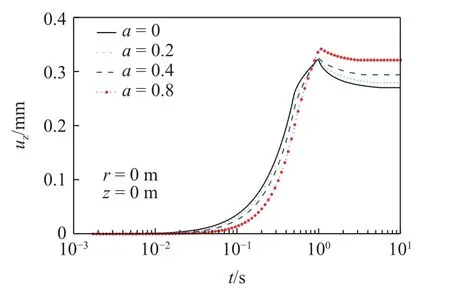
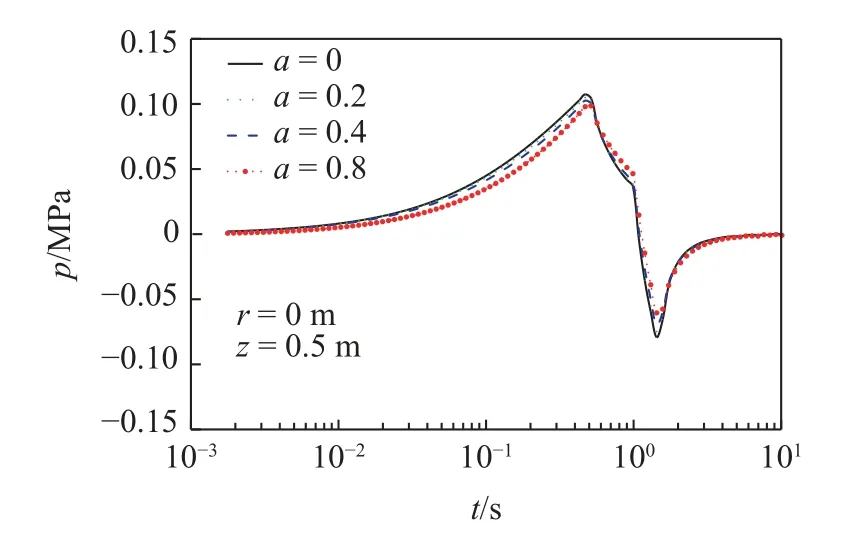
式中,σ和ε分别为应力和应变;Es为弹簧元件K的弹性模量;η,a分别为黏壶N的黏滞系数和黏性阶数;t为时间变量.从式(1)能够看出,当a=0 时黏壶N退化为线弹性固体,a=1 时黏壶N退化为理想Newton 流体,0 对任意时域函数f(t)引入如下Lapace 变换 利用式(2)对式(1)做Laplace 变换,得到 式(3)反映了分数阶Kelvin 模型在Laplace 变换域的应力-应变关系,其中复模量. 将式(3)拓展到三维应力状态,并写为张量形式为 式中v为泊松比. 如图2 所示,半空间饱和黏土地基表面作用半径为r0的圆形分布载荷q,根据力学模型的轴对称性,建立柱坐标系r-φ-z.基于Biot 多孔介质理论,并考虑土骨架和孔隙水的惯性耦合,饱和黏土的固结平衡方程为 图2 饱和黏土地基固结模型Fig.2 Consolidation model of saturated clay ground 式中,u和w分别为土骨架和孔隙水的位移张量;p为孔隙水压力;ρ=(1-n)ρs+nρf为土体总密度,其中ρs和ρf分别为固体颗粒和孔隙水的密度;γw=ρfg为水的重度,g为重力加速度;kf为渗透系数.∇表示Hamilton 算子,在柱坐标下,;上标“·”和“··”表示对时间t的一阶和二阶导数.σa为作用在多孔介质微元上的总应力,p为孔隙压力.规定压应力为正方向,则根据有效应力原理有 式中,σ'为土骨架有效应力张量,αs为反映土颗粒压缩性的Biot 系数. 渗流连续性方程为 式中,M为Biot 系数,表征孔隙水的压缩性. 将分数阶Kelvin 模型应用于土骨架,即有效应力σ'满足式(4).将式(4)和式(8)代入式(6),并考虑几何关系(ε=(∇u+u∇)/2),整理后得到位移形式的固结平衡方程为 式中Kd=ρf s2/n+γws/kf. 本文根据加载、卸载特征,考虑3 种时变载荷. (1)斜坡载荷 如图3(a)所示,载荷由t1时段线性增大至q0后保持恒载,不卸载,加载时长te=t1.载荷的时域变化函数描述为 图3 时变载荷示意图Fig.3 Diagram of time dependent load 式中,H()为Heaviside 阶跃函数,其定义为 (2)三角形载荷 如图3(b)所示,载荷由t1时段线性增大至q0后随即线性卸载,卸载时长tu=t2-t1.载荷的时域函数描述为 (3)梯形载荷 如图3(c)所示,载荷由t1时段线性增大至q0后保持恒载,在t2时刻开始线性卸载,恒载时长td=t2-t1,卸载时长tu=t3-t2.载荷的时域函数描述为 载荷在地表的作用区域为0≤r≤r0,则时变载荷q在空间、时间域的解析函数描述为 对径向坐标r引入如下Hankel 变换 将式(11)~式(13) 代入式(14),而后利用式(2)和式(15)进行Hankel–Laplace 联合变换,则分别得到斜坡、三角形和梯形载荷的变换域函数. 斜坡载荷 三角形载荷 梯形载荷 本文考虑初始条件下位移、应力及孔隙压力均为0,对式(9)做Lpalace 变换,并整理为 对式(7)和式(10)两边取散度,再将式(19)代入后得到 对式(20)做0 阶Hankel 变换,而后整理为常微分方程组 式中 利用常指数基础解系,将方程组(21)的通解设为 式中,γ为方程组(22)的特征根,Pf,Pθ为对应的函数幅值. 将式(22)代入式(21),得到线性方程组 由式(23)解得 利用式(23)的非0 解条件,得到 式中,β=γ2,B1=a11+a21,B2=a11a21-a12a22. 求解式(25) 得出βm(m=1,2),并进一步得出4 个特征根 式中,Cm,Dm(m=1,2)为待定系数.本文中地基模型为无限半空间,在无穷深度处(z→∞),所有场量需衰减为0,从而得出Cm=0. 将式(27)代入式(10),并利用体应变与位移的关系(θ=∇·u),进一步得出土骨架的位移通解为 考虑地表(z=0)为自由边界,且完全透水,则地表边界条件描述为 对式(30)运用Hankel-Laplace 变换,则得到 将孔压和应力通解代入式(31),则得到关于D0,D1和D2的线性方程组 式中,M为3×3 系数矩阵,其矩阵元素为 通过矩阵运算得出待定系数D0,D1和D2为 式中,[ ]T表示矩阵的转置,[ ]-1表示逆矩阵.将已计算出的D0,D1和D2回代到位移和应力通解中,则得到变换域中位移、应力及孔隙压力解.利用Parseval法[32]和Crump 法[33]进行Hankel-Laplace 数值反演得出时空域解,数值反演公式为 Hankel 反演 Laplace 反演 式中,Re,Im 分别表示取实部和虚部;ϑ,T为自由参数,计算中取T=2t,ϑ=5/T;N为级数截取项数,取N=256 时能很好地满足精度[32]. 将式(16)代入系统控制方程,并利用表1 中的参数值,计算斜坡载荷作用下饱和黏土地基的固结响应.文献[29]将土骨架考虑为线弹性本构,计算了饱和土地基在斜坡变载荷作用下的固结问题.图4和图5 首先取黏性阶数a=0,将土骨架退化为弹性本构模型与文献解进行对比.结果显示,无论位移还是孔隙压力,本文退化解与文献解都能较好吻合.由图4可知,当考虑土骨架的黏性流变后(a=0.5),饱和黏土在主固结阶段的沉降速率较慢,而次固结阶段的沉降速率加快,而且长期沉降量增大.图5 显示,土骨架黏性流变使孔隙压力峰值减小,而且孔压消散速率略小于弹性骨架. 表1 计算参数表[29]Table 1 Table of calculation parameters[29] 图4 位移结果对比Fig.4 Comparison of displacement results 图5 孔隙压力结果对比Fig.5 Comparison of pore pressure results 图6 和图7 考察了不同加载时长下位移和孔隙压力随时间的变化.图6 显示,加载时长te越大(加载速率越小),主固结阶段的沉降速率越慢,但长期沉降量相同.由图7 可知,加载速率越小,孔隙压力峰值越小.这是由于加载时长较大时,在加载过程中孔压能够及时消散,孔压累积效应减小. 图6 不同加载时长下的位移结果(a=0)Fig.6 Displacement under different loading durations (a=0) 图7 不同加载时长下的孔隙压力结果(a=0)Fig.7 Pore pressure under different loading durations (a=0) 图8 和图9 给出了不同黏性阶数下位移和孔隙压力随时间的变化.由图8 可知,土骨架黏性流变对主固结阶段的沉降速率和长期沉降均产生影响.土骨架黏性阶数越大(流变性越强),主固结阶段的沉降速率越小,而长期沉降量越大,说明土骨架流变性显著增大了次固结阶段的沉降速率.图9 显示,土骨架流变性使孔隙压力的峰值减小,孔压消散速率减缓,说明土骨架流变性对孔隙水渗透具有抑制作用. 图8 不同黏性阶数下的位移结果(te=0.5 s)Fig.8 Displacement under different viscous orders (te=0.5 s) 图9 不同加载时长下的孔隙压力结果(te=0.5 s)Fig.9 Pore pressure under different viscous orders (te=0.5 s) 将式(17)代入系统控制方程,计算饱和黏土地基在三角形载荷作用下的固结响应.图10 和图11在保持加载时长相同的情况下(te=0.5 s),考察了卸载速率对固结过程中位移和孔隙压力的影响.图10显示,卸载时地基土发生变形恢复,卸载结束后位移收敛于恒定值.卸载时长tu越短(卸载速率越大),位移峰值略有减小,但发生的变形恢复量较大,造成地基长期沉降量减小.由图11 可知,卸载时地基土中出现负孔压,卸载速率越大,负孔压越大.这是由于变形恢复时,土骨架弹性扩张产生负向孔压;卸载速率越快,孔隙水渗透不及时,将产生更大的负向孔压. 图10 不同卸载时长下的位移结果(te=0.5 s,a=0)Fig.10 Displacement under different unloading durations(te=0.5 s,a=0) 图11 不同卸载时长下的孔压结果(te=0.5 s,a=0)Fig.11 Pore pressure under different unloading durations(te=0.5 s,a=0) 图12 和图13 反映了三角形载荷作用下土骨架黏性阶数对位移和孔隙压力的影响.由图可知,土骨架流变性使地基土在卸载时发生的变形恢复量减小,因而产生的负孔压相应减小.通过对比加载阶段和卸载阶段的曲线形态,能够发现,在加载阶段流变对位移和孔压的影响大于卸载阶段. 图12 不同黏性阶数下的位移结果(te=tu=0.5 s)Fig.12 Displacement under different viscous orders (te=tu=0.5 s) 图13 不同黏性阶数下的孔压结果(te=tu=0.5 s)Fig.13 Pore pressure under different viscous orders (te=tu=0.5 s) 将式(18)代入系统控制方程,计算梯形载荷作用下位移和孔隙压力响应.图14 和图15 在保持加载时长和卸载时长相同的情况下(te=tu=0.5 s),考察了梯形加载过程中恒载时长td对位移和孔隙压力的影响.图14 显示,恒载时长越大,土体固结程度越高,位移峰值和长期沉降量都越大,卸载时的变形恢复量也较大.由图15 可知,恒载时长越大,卸载时产生的负孔压也相应增大. 图14 不同恒载时长下的位移结果(te=tu=0.5 s)Fig.14 Displacement under different dead load durations (te=tu=0.5 s) 图15 不同恒载时长下的孔压结果(te=tu=0.5 s)Fig.15 Pore pressure under different dead load durations (te=tu=0.5 s) 图16 和图17 在保持加载时长和恒载时长相同的情况下(te=td=0.5 s),考察了卸载时长tu对固结响应的影响.图16 显示,梯形载荷作用下,卸载产生的变形恢复小于三角形载荷.这是由于梯形载荷通过恒载阶段使土体充分固结,因而卸载时的变形恢复减小.图17 则表明,梯形载荷在卸载阶段的孔隙压力变化形态与三角形载荷相同.图18 和图19 给出了梯形载荷作用下,黏性阶数对位移和孔隙压力的影响.对比三角形载荷发现,当黏性阶数较大时,梯形载荷作用下位移在恒载阶段大幅增大,导致位移峰值和长期沉降量都明显增大.这是由于黏性阶数较大时,土体在恒载阶段的次固结沉降增大,造成位移峰值和长期沉降量增大. 图16 不同卸载时长下的位移结果(te=td=0.5 s)Fig.16 Displacement under different unloading durations (te=td=0.5 s) 图17 不同卸载时长下的孔压结果(te=td=0.5 s)Fig.17 Pore pressure under different unloading durations (te=td=0.5 s) 图18 不同黏性阶数下的位移结果(te=td=tu=0.5 s)Fig.18 Displacement under different viscous orders (te=td=tu=0.5 s) 图19 不同黏性阶数下的孔压结果(te=td=tu=0.5 s)Fig.19 Pore pressure under different viscous orders (te=td=tu=0.5 s) 利用分数阶Kelvin 模型描述土骨架的黏性流变,结合Biot 多孔介质理论构建饱和黏土地基的三维轴对称固结模型.考虑斜坡、三角形和梯形3 种载荷工况,研究了饱和黏土地基的固结特性.通过算例分析,总结出以下几点结论. (1)土骨架流变性对孔隙水渗透具有抑制作用,使土体在主固结阶段沉降速率减缓,次固结阶段沉降速率加快,而且长期沉降量增大. (2)卸载阶段土体会发生变形恢复,土骨架弹性扩张产生负孔压.土骨架黏性流变越强,变形恢复量越小,产生的负孔压也越小. (3)载荷类型和加载路径主要影响固结过程中位移和孔压随时间的变化形态,而土骨架黏性流变影响土体的长期沉降量.1.2 饱和黏土地基固结模型
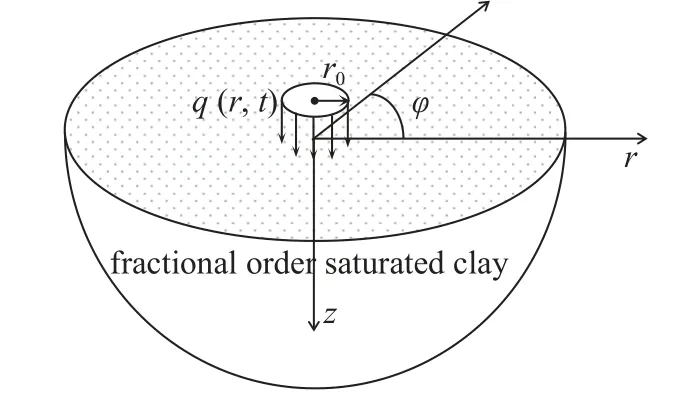
1.3 时变载荷的数学描述
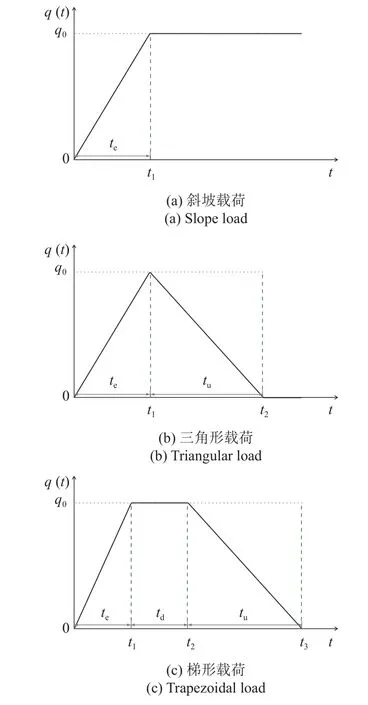
2 控制方程求解
3 算例分析
3.1 斜坡载荷



3.2 三角形载荷



3.3 梯形载荷



4 结论

