正方形布置四圆柱结构流致振动响应特性研究1)

胡中明 王嘉松 孙远坤 郑瀚旭 范迪夏

* (黄淮学院建筑工程学院,河南驻马店 463000)

† (上海交通大学船舶海洋与建筑工程学院,上海 201100)

** (西湖大学工学院,杭州 310030)

引言

多圆柱结构广泛存在于许多工程领域,如大跨度桥梁结构的缆索系统、换热器中的热交换管束、高压长距离输电线、海底管线和海洋油气开采中的生产立管系统等.不同于单圆柱结构的涡激振动响应(一般呈现典型的自限振动)[1-2],多圆柱结构之间会发生复杂的耦合干涉作用,产生比单圆柱结构更为复杂的流致振动响应,如下游圆柱所诱发的尾流致振(wake-induced vibration,WIV)[3-4],尾流驰振(wake-induced galloping,WIG)[5-6]等.持续剧烈的振动会给圆柱结构带来诸如碰撞和疲劳损伤等危害,影响结构的安全性和使用寿命.因此,开展多圆柱结构的流致振动研究具有重要意义.

目前,针对多圆柱结构中处于基础地位的双圆柱结构流致振动问题,国内外学者开展了系列研究,结果表明,受间距和布置方式的影响,圆柱结构的振动响应呈现不同特性[7-13].例如,对于串列双圆柱结构,Xu 等[12]通过水槽实验研究表明当S/D=2.57,3.57,4.57 较大间距时(S为两圆柱圆心间距,D为圆柱直径,下同),在约化速度Ur<12 区间内,上游圆柱受下游圆柱的影响较小其振动响应特性类似于单圆柱,而当S/D=1.57 小间距时,上游圆柱振动非常剧烈呈现类驰振响应,这种现象在Kim 等[7]以及Hu等[13]的风洞实验中也可以观测到;而下游圆柱则在整个测试间距范围内呈现类涡激振动现象.对于并列双圆柱结构,Huera-Huarte 等[14]通过水槽实验研究了间距比为2.0≤S/D≤5.0 时并列柔性双圆柱的流激振动响应,研究发现当S/D<3.5 时,两圆柱的横流向振动位移为同相位或者反相位关系,此时圆柱之间存在较强的耦合作用,呈现耦合的涡激振动(wake-coupled VIV,WCVIV),而当S/D>3.5时,两圆柱显示不同步运动,表明此时圆柱之间的耦合作用非常弱,类似单圆柱结构的涡激振动.近年来,Xu 等[15]通过拖曳水池研究了Re=800～16000,S/D=3.0,4.0,6.0 和8.0 条件下并列双圆柱的流致振动问题,研究表明,并列双圆柱的横流向振动幅值会在相同约化速度处达到最大值,当间距比S/D≤6.0 时,横流向存在明显的邻近干涉作用,最大呈现4 阶主导模态.Han 等[16]采用基于上述实验中的位移数据,采用逆向识别方法重构了并列双圆柱的流体力特性.结果显示当S/D≤6.0 时,两圆柱的横流向流体力响应频率明显不同,并且附加质量系数也存在明显偏差,这为实际工程中海洋立管的流激振动提供了重要的参考价值.此外,胡中明等[17]通过风洞实验也发现了在间距比S/D≤3.0 时,并列双圆柱之间相互干涉作用较强,双圆柱振动幅值响应呈现不一致性,振动位移之间表现为同相位或反相位耦合特征,圆柱尾流场对称点的涡脱频率也不相同,尾流呈现不对称性.而当间距比S/D=3.5～4.0 时,双圆柱振动幅值和涡脱频率几乎相同,尾流的不对称现象消失,这和陈威霖等[18]数值模拟研究结论类似.

上述研究使人们认识了双圆柱结构的耦合干涉特征,但是由于实际工程中多圆柱结构的数量和布置方式会更加复杂,为探明其流致振动响应特性,以正方形布置四圆柱结构为代表的多圆柱结构的流致振动响应问题引起了一些研究人员的关注[19-23].例如,Zhao 等[19]通过数值方法研究了4 个圆柱都可以横向自由振动的问题,此时m*=2.5,S/D=1.5～4.0,Re=150,可以观察到4 种不同的振动响应类型,即同相位模式、反相位模式、不相关模式与这些不同的振动响应类型和圆柱的间距密切相关.及春宁等[20]利用浸没边界法对间距m*=2.0,S/D=5.0,Re=100,Ur=2.0～50.0 时的正方形布置四圆柱的流致振动响应进行了数值模拟.结果表明,上游两个圆柱的响应和单圆柱涡激振动类似,但是下游两个圆柱的振动幅值非常大,比单圆柱涡激振动最大振幅增大了74.8%,由于圆柱间隙流的偏斜,4 个圆柱的流激振动会出现3 个不对称的区间.最近,Ma 等[23]通过拖曳水槽研究了m*=1.9,S/D=6.0,Re=16000 时,正方形布置四柔性圆柱的水动力学响应.结果表明,上游两圆柱的振动特性和并列圆柱布置时类似,受下游圆柱的影响有限;而下游两圆柱会受到上游圆柱尾流的影响,其横流向的振动频率比单圆柱略低,顺流向的振动频率显著降低接近横流向振动频率,最终呈现椭圆形运动轨迹.

综上所述,相比双圆柱结构,正方形布置四圆柱的流致振动响应特性更加复杂,虽然目前针对此问题已经取得了一定的研究成果,但是一方面仍然缺乏高雷诺数和大质量比条件下正方形布置四圆柱流致振动的实验研究,而质量比则是影响圆柱等钝体结构流致振动的重要参数;另一方面需要研究双圆柱结构和正方形布置四圆柱结构流致振动特性的关系.因此,本文通过风洞实验研究正方形布置四圆柱的动力学响应,包括结构模型无量纲振动幅值A/D、振动频率fo和涡脱频率fs等,以期探明大质量比条件下正方形布置四圆柱的流致振动特性,以及双圆柱结构和正方形布置四圆柱动力学响应之间的关系,进而为揭示工程中更加复杂的多圆柱的动力学响应提供有意义的参考和指导.

1 实验研究方法

本文实验研究是在上海交通大学动力机械与工程教育部重点实验室所属的低速风洞中完成的.风洞实验段长、宽、高的几何尺寸分别为2000 mm,600 mm,600 mm,在实验测试条件下湍流度始终小于0.2%,更加详细的信息可以参考文献[6,13].

4 根圆柱模型分别被命名为圆柱1 (cylinder 1)、圆柱2 (cylinder 2)、圆柱3 (cylinder 3) 和圆柱4(cylinder 4),其中圆柱模型1,2 在上游,圆柱3,4 在下游,圆柱模型安装具体示意图如图1 所示.圆柱横向放置在风洞实验段,两端分别用4 根对称弹簧固定在风洞壁上.为保证4 根圆柱结构都可以在横向自由振动,需要重点考虑横流方向圆柱1 和2 的并列空间布置(下游圆柱3 和4 与上游圆柱1 和2 情况类似),因此在确保所有模型结构参数以及支撑弹簧刚度相同的情况下,使上游圆柱1 的支撑弹簧间距较窄(绿色示意)而上游圆柱2 支撑弹簧间距较宽(紫色示意),同时上游圆柱1 和2 的支撑弹簧不在同一平面内,这样就保证上游圆柱1 和2 可以自由振动而不因为空间相互影响,如图1(b)所示.

图1 正方形布置四圆柱实验模型示意图Fig.1 Configuration of four elastically mounted cylinders in square arrangement

4 个圆柱弹簧刚度k均约为254 N/m.圆柱直径D为40 mm,厚度为2 mm,长度为500 mm,长径比为12.5.来流速度U=1.2～10.7 m/s,相应的雷诺数范围为Re=3200～28900,此时处于亚临界区.4 根圆柱模型的质量分别为260.2 g,259.9 g,260.1 g 和260.0 g,相应的质量比m*分别为345.3,344.9,345.1 和345.0.通过一系列施加激励后的自由衰减实验可以近似估算得到4 个圆柱模型的阻尼比ξ分别为0.140%,0.135%,0.137%和0.142%.模型的固有频率通过对自由衰减实验中所测的位移进行FFT变换获得,分别约为14.05 Hz,14.06 Hz,14.06 Hz 和14.06 Hz,以圆柱模型4 为例,自由衰减的位移曲线和位移信号频谱图如图2 所示.模型结构的主要参数如表1 所示.

表1 模型结构的主要参数Table 1 Structural parameters of the model

图2Fig.2

4 个圆柱模型的振动位移信号y通过自主搭建的同步位移测试系统进行测量,进一步对y进行FFT 处理可以得到圆柱模型的振动频率fo.同步位移测试系统主要包括激光位移传感器(KEYENCE IL-600)、数字信号放大器(KEYENCE IL-1000)、多通道采集卡(Advantech 64 通道PCI-1747 U)、端子板、工控机(Advantech PCI-610 H)和采集程序等.

为了展示上述系统的测量细节,同时对系统测量的不确定性进行必要的分析,选取质量阻尼比m*ξ=0.490 的下游圆柱4 为代表来进行误差分析,其余工况实验数据误差范围大致和所选的代表圆柱模型类似.包含误差棒的下游圆柱4 的无量纲振动幅值响应如图3 所示,误差棒越大说明不同振动周期间的偏离程度越大.由图3 可知,所有约化速度下的实验数据的标准差都较小,最大值不超过0.03,这说明振动过程相对规律,周期与周期之间没有发生大的偏移.测量细节及振动的相对规律性也可以通过图3 中所选取的两个约化速度下的振动位移历史曲线来示例说明.

图3 含有标准差的圆柱4 的无量纲振动幅值响应Fig.3 Nondimensional amplitude response associating with standard deviations of cylinder 4

圆柱模型尾流场中的流向脉动速度u则是通过多通道热线风速仪测试系统测量得到,两个热线探头HW1 和HW2 (Dantec 55 p11)分别距离圆柱3 和4 的中心水平距离为4D,竖向距离为1D,如图1 所示.进一步对u进行FFT 处理可以得到圆柱模型尾流场的涡脱频率fs.本实验所用的多通道热线风速测试系统的测试速度范围为0.5～60 m/s,测量精度可达0.1%,热线探头具有高达10 kHZ 的响应频率,可以准确捕获圆柱模型尾流场布置点处流速随时间的变化规律,进而获得比较准确的涡脱频率.

2 实验方法验证

首先进行一系列单圆柱涡激振动实验以验证本文实验测试方法的可靠性,分别选取圆柱1 (m*ξ=0.48)和圆柱4 (m*ξ=0.49)实验结果与前人实验结果进行对比,如图4 所示.图4 中纵坐标A/D为无量纲均方根幅值,是将位移信号的均方根值yrms乘以再除以模型直径D得到,即

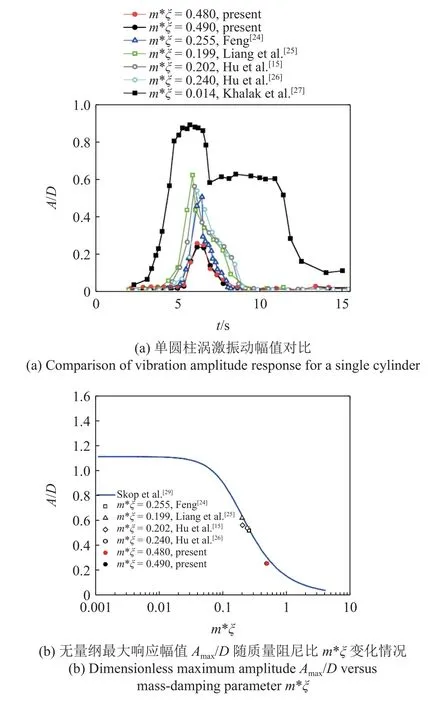
图4Fig.4

从图4(a)中可以观察到圆柱1 和圆柱4 均呈现经典的涡激振动锁定响应(lock-in),锁定区间大约在Ur=4.9～8.6 区间内,与Feng[24](m*ξ=0.255),Liang 等[25](m*ξ=0.199),Hu 等[13,26](m*ξ=0.202,0.240)等风洞中大质量阻尼比实验结果类似,都呈现两个经典分支,即初始分支和下端分支.在初始分支,A/D随着Ur增大而增大,在Ur≈ 6.1 达到最大值,随后A/D开始衰减直至为0.但是对比Khalak 等[27](m*ξ=0.014)的水槽中小质量阻尼比实验结果,除了初始分支和下端分支外,还会存在一个振动位移非常大的上端分支,不同文献中振动幅值及锁定区间的差异主要是因为实验中圆柱的质量阻尼比不同引起的.

为了进一步验证本实验结果的准确性,将无量纲振动幅值的最大值(Amax/D)随质量阻尼比的变化和前人大量实验结果进行对比,如图4(b)所示.图4(b)中蓝颜色是Griffin[28]和Skop 等[29]在总结了大量前人实验结果后拟合出的一条经验曲线.由图4(b)可知,目前的测试结果和经验曲线吻合较好.上述实验结果证明本实验测试方法可靠性较高.

3 正方形布置四圆柱结构的流致振动响应特性

3.1 振动幅值响应特性

图5 展示了正方形布置四圆柱(图5 中分别命名为cylinder 1,cylinder 2,cylinder 3 和cylinder 4)无量纲振动幅值A/D随圆柱间距S/D和约化速度Ur的变化规律,可以看到4 个圆柱对间距S/D和约化速度Ur的变化非常敏感,会呈现不同模式的振动响应.同时为了研究正方形布置四圆柱和串列(tandem cylinders)、并列(side-by-side cylinders)双圆柱系统振动幅值响应的关系,分别选取串列、并列双圆柱时的代表性间距S/D=1.5,4.0 的结果[13,17]包含在图5(a)和图5(e)中.

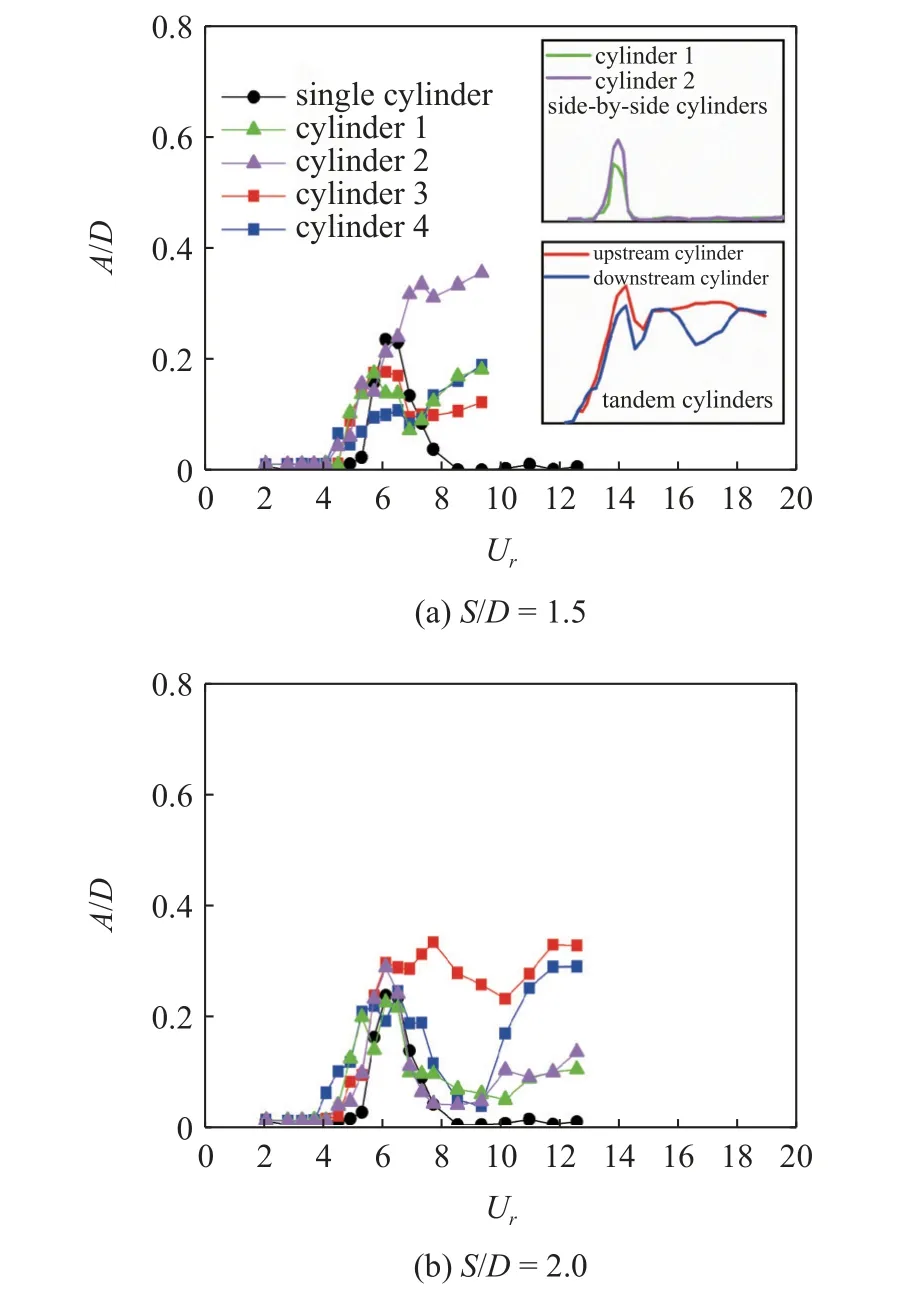
图5 正方形布置4 个圆柱的振动幅值响应Fig.5 Vibration amplitudes responses of four cylinders in square arrangement

由图5(a)可知,当间距S/D=1.5 时,可以观察到4 个圆柱几乎都在约化速度Ur=4.5 时开始振动,上游圆柱1 的振动幅值在4.5≤Ur≤7.3 时先增大后减小,表现为一个凸起现象(涡激振动响应),并在约化速度Ur>7.3 之后振动幅值随着约化速度增加而增加(类弛振响应),但是振动幅值要比上游圆柱2 小很多(A/D的最大值为0.19).上游圆柱2 的幅值随着约化速度的增长而迅速增加并在约化速度Ur=5.3 处获得局部最大值A/D=0.16,随后又略微减小(涡激振动响应),但在约化速度Ur≥ 6.1 之后再次随着约化速度的增加而增加(类弛振响应),圆柱的最大振动幅值为0.36,相比于其他3 个圆柱要大很多;上游圆柱1 和2 表现为不对称的振动幅值响应趋势,这和并列双圆柱在间距S/D=1.5 时振动幅值响应趋势的不对称规律保持一致.以往研究表明,对于串列双圆柱,由于下游圆柱的存在会使上游圆柱呈现振动剧烈的类弛振响应[7,13],因此在正方形四圆柱中,上游圆柱1 和2 会呈现不对称的耦合的涡激振动和类弛振响应,而不像并列双圆柱那样仅表现为类似于单圆柱典型的涡激振动响应趋势.同样,下游圆柱3 和4 的振动幅值首先都呈现随约化速度的先增大再减小的涡激共振响应,然后再耦合上随约化速度增加而增加的尾流弛振响应,这和串列双圆柱中下游圆柱的振动幅值响应规律也保持一致,但是由于此时4 个圆柱之间的干涉作用非常强,所以下游圆柱3 和4 的振动幅值响应趋势也呈现不对称性.

需要说明的是,上游圆柱1 和2 所发生的涡激振动和下游圆柱所表现的涡激共振都是一种共振现象,振动幅值都表现为先增大后减小的凸起形式,但是由于上游圆柱和单圆柱一样面对的是均匀来流,而下游圆柱面对的是上游圆柱的尾流,所以为了加以区别,将上游圆柱的振动称为涡激振动,而把下游圆柱的振动称为涡激共振.

上游圆柱的类弛振和下游圆柱的尾流弛振振动特征虽然都大致表现为振动幅值随约化速度的增加而增加的趋势,但是两者的机理却不相同.尾流弛振主要指的是处于上游圆柱尾流中的下游圆柱由于间隙流转换作用[30]或者上游圆柱完整脱落的旋涡和下游圆柱结构耦合作用而诱发的剧烈振动[3],而类弛振响应指的是直面均匀来流的上游圆柱所呈现的类似于典型弛振的剧烈振动趋势,主要由于上游圆柱近尾流一定区域存在下游圆柱型结构物.Bokaian等[31]在水槽实验中也发现,如果在上游圆柱的近尾流中布置一个固定的下游圆柱时,上游圆柱会呈现驰振响应.他们强调发生驰振响应的必要条件是下游圆柱刚好处于上游圆柱近尾流的合适位置.所以为了加以区别,将直面均匀来流的上游圆柱振动幅值随约化速度增加的剧烈振动称为类弛振响应,而将下游圆柱类似的振动趋势称为尾流弛振.

综上,由图5(a) 的结果可知,当间距S/D=1.5 时,虽然4 个圆柱是按照正方形对称布置的,但是4 个圆柱的振动幅值响应趋势并不对称,上游圆柱1 和2 之间以及下游圆柱3 和4 之间的幅值响应都不同,尤其是上游圆柱之间的差异更加明显,这说明间距较小时,4 个圆柱之间存在强烈的干涉作用,相互之间影响非常复杂,下游圆柱3 不仅会受到上游圆柱1 的影响,还会受到上游圆柱2 以及下游圆柱4 的影响,同样上游圆柱1 不仅会受到下游圆柱3 的影响,还会受到上游圆柱2 以及下游圆柱4 的影响.当约化速度Ur>9.4 之后,圆柱之间会发生碰撞,此时位移传感器所采集的振动信号发生突变,因此在S/D=1.5 时,所测试的约化速度范围比较小.

当间距S/D=2.0 时(图5(b)),可以观察到上游圆柱1 和2 都呈现耦合的涡激振动和类弛振响应,但是两圆柱之间的差异在减小,这说明此时下游圆柱3 和4 对上游圆柱1 和2 以及上游两个圆柱之间的相互干涉影响都在减弱.反过来,下游圆柱3 和4 虽然也都呈现耦合的涡激共振和尾流弛振响应,但是其振动幅值相差仍然很大,尤其是约化速度在6.9≤Ur≤10.2 区间时,下游圆柱3 的最小振动幅值A/D=0.23,而圆柱4 的最小振动幅值仅为A/D=0.0 4.这说明上游圆柱1 和2 仍然会同时对下游两圆柱产生影响并且下游两圆柱之间的相互影响仍存在.需要注意的是当Ur>14.2 之后,圆柱之间会发生碰撞.

当间距S/D=2.5 时(图5(c)),对于上游圆柱1 和2 而言,除了在约化速度Ur≥ 9.4 (上游圆柱1)和Ur≥ 11.8 (上游圆柱2)之后呈现微弱振动外(A/D的最大值为0.07),模型的振动幅值接近单圆柱典型的涡激振动响应,此时下游圆柱对上游圆柱的影响进一步减弱.下游圆柱3 在区间5.3 18.9 之后,圆柱之间会发生碰撞.

随着间距的进一步增大,当S/D=3.0～4.0 时,由图5(d)和图5(e)可知上游圆柱1 和2 越来越接近单圆柱,例如当间距S/D=4.0 时,上游圆柱1 和2 的振动响应和串列双圆柱中上游圆柱振动幅值响应规律类似,都呈现典型的涡激振动响应,结合图中并列双圆柱的振动幅值响应特征,说明此时上游的两个圆柱1 和2 已经不再受其它相邻圆柱的影响,几乎和单圆柱一样.而下游圆柱3 和4 也和串列双圆柱中下游圆柱振动幅值响应规律类似,都呈现一种分离的涡激共振和尾流弛振响应,即在约化速度较小时模型表现为涡激共振响应,当约化速度大于一定值时表现为尾流弛振响应,而在两者之间圆柱的振动非常微弱.并且随着间距的增加,下游圆柱3 和4 的振动响应越来越接近,这表明当间距较大时,正方形布置的4 个圆柱中的第一行的两个圆柱(圆柱1 和3)和第二行的两个圆柱(圆柱2 和4)类似于大间距串列布置的双圆柱情形,即上游圆柱1 只影响下游圆柱3,上游圆柱2 只影响下游圆柱4,上游圆柱1 和2 之间以及下游圆柱3 和4 之间都不会相互影响.由于此时圆柱间距足够大,一直到实验中最大约化速度时,4 个圆柱之间都未发生碰撞.

综上,结合串列和并列双圆柱以及图5 中正方形布置四圆柱的振动幅值响应结果,可以得出串列、并列双圆柱和正方形布置四圆柱的振动幅值响应趋势上存在着很多共同的特征,如并列双圆柱在间距较小时会呈现不对称的振动趋势而正方形布置的四圆柱也会呈现不对称的振动趋势,当间距大于一定值时并列双圆柱和正方形布置的上游圆柱1 和2 (下游圆柱3 和4)都呈现几乎相同的振动响应趋势.串列双圆柱中上游圆柱的振动幅值随间距的增加会分别呈现耦合的涡激振动和类弛振响应以及典型的涡激振动(和单圆柱类似),正方形布置四圆柱中的上游圆柱1 和2 也会呈现类似的振动响应规律;同样,串列双圆柱中下游圆柱的振动幅值随间距的增加会分别呈现耦合的涡激共振和尾流弛振响应以及分离的涡激共振和尾流弛振响应,而正方形布置四圆柱中的下游圆柱3 和4 也会呈现类似的响应.为了更加形象地展示正方形四圆柱的动力学响应特征以及与双圆柱结构之间的关系,现将其动力学响应结果汇结在图6 中.

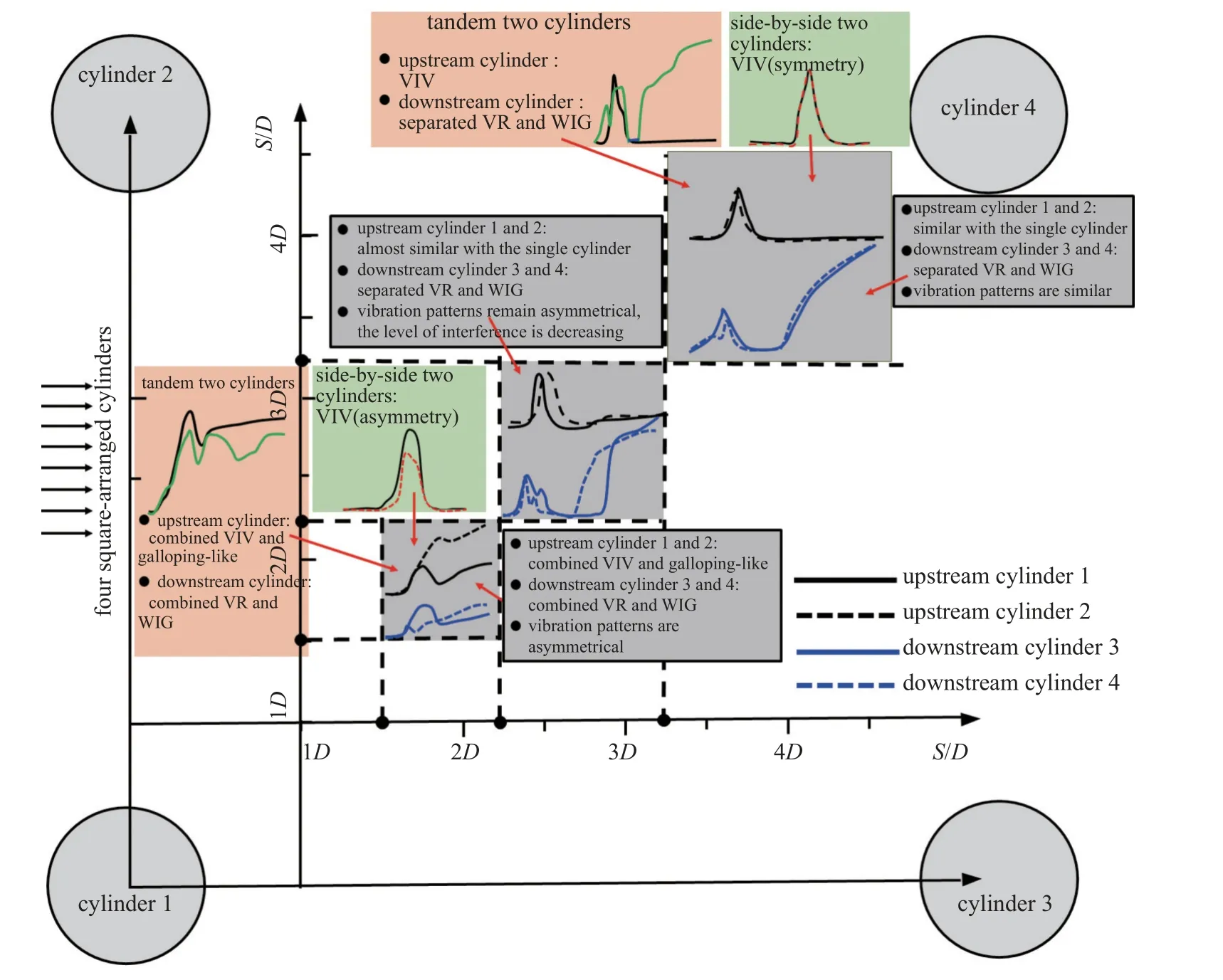
图6 正方形布置四圆柱的流致振动响应模式及与双圆柱的关系Fig.6 Vibration patterns for the four square arrangement cylinders and the relationship between four square and two cylinders

3.2 涡脱频率特性

为了进一步理解振动幅值响应特性机理,本小结开始讨论无量纲涡脱频率fs/fn随S/D的变化规律.涡脱频率图中红色越亮,代表无量纲涡脱频率fs/fn的PSD 幅值越大,主频越明显,分别选取代表性的间距S/D=1.5,2.5,4.0 时的结果来阐述说明.

图7 给出了在间距S/D=1.5 时,圆柱尾流场中的无量纲涡脱频率fs/fn随约化速度Ur的变化情况.具体来说,当约化速度Ur<4.5 时,此时4 个圆柱都不振动,下游圆柱3 和4 尾流场中的无量纲涡脱频率fs/fn都随着约化速度的增加沿着St≈0.19 线性变化,这和固定圆柱涡脱频率特性类似.当约化速度Ur≥ 4.5 之后,4 个圆柱开始振动,无量纲涡脱频率fs/fn呈现锁频现象.虽然圆柱1(2)和3(4)都会呈现耦合的涡激振动(涡激共振) 和类弛振(尾流弛振)响应,但是下游圆柱3 尾流场中的涡脱频率fs会一直锁定在1 倍的固有频率fn上,而下游圆柱4 尾流场中的涡脱频率fs在约化速度Ur≥ 6.9 后会锁定在fn的多倍频上,这是因为此时上游圆柱2 振动非常剧烈,会伴随着复杂的泄涡模式.

图7 S/D=1.5 时无量纲涡脱频率,(a)振动幅值,(b)圆柱3 后的涡脱频率,(c)圆柱4 后的涡脱频率Fig.7 Response of the normalized vortex shedding frequency fs/fn at S/D=1.5,(a)vibration amplitude,(b)fs/fn behind cylinder 3,(c)fs/fn behind cylinder 4

和并列双圆柱类似,无量纲涡脱频率fs/fn响应的不同再次说明了4 个圆柱之间存在复杂的相互干涉作用,存在不对称的尾流场,进而导致圆柱呈现不对称的振动趋势.同时,图7(b)中,在区间4.5≤Ur≤8.1 之间还有一个比较明显的fs/fn≈0.5 的频率,这说明此时一个周期内除了泄放一对2S 涡外,还会泄放其他的旋涡,这也意味着在间距很小时,正方形布置方式圆柱之间的相互作用和串列布置方式有很大的不同.

当间距S/D=2.5 时下游圆柱3 和4 尾流场的无量纲涡脱频率fs/fn随约化速度Ur的变化情况如图8(b)和图8(c)所示.可以看到两个圆柱的无量纲涡脱频率响应都分为4 个区域,对于下游圆柱3 而言,在2.1≤Ur≤5.1 和7.7≤Ur≤10.2 两个区间内,无量纲涡脱频率fs/fn会随着约化速度的增加沿着St≈0.17 线性变化,此时下游圆柱3 振动非常微弱.而在这两个区间之外,fs/fn会发生锁频现象,即在5.1 10.2 时,涡脱频率fs随着约化速度的增长会逐渐锁定在1 倍、2 倍甚至4 倍的固有频率fn上,此时下游圆柱3 的振动非常剧烈,其振动幅值随着约化速度的增加而增加表现为尾流弛振响应.

图8 S/D=2.5 时无量纲涡脱频率,(a)振动幅值,(b)圆柱3 后的涡脱频率,(c)圆柱4 后的涡脱频率Fig.8 Response of the normalized vortex shedding frequency fs/fn at S/D=2.5,(a)vibration amplitude,(b)fs/fn behind cylinder 3,(c)fs/fn behind cylinder 4

下游圆柱4 尾流场中的无量纲涡脱频率fs/fn和下游圆柱3 类似,即在2.1≤Ur≤4.5 和8.5≤Ur≤11.0 区间内随着约化速度的增加近似沿着St≈0.18 线性变化,此时下游圆柱4 振动非常微弱,但是需要注意的是,在一些约化速度Ur情况下没有明显的主频,呈现无规律特性,这说明下游圆柱3 和4 虽然振动都非常微弱但是尾流场的fs/fn响应却并不完全相同,四个圆柱之间仍然有相互干涉作用.同样在4.5 11.0 时涡脱频率fs随着约化速度Ur的增长会逐渐锁定在固有频率fn的多倍谐频上,此时下游圆柱4 的振动幅值随着约化速度的增加而增加,呈现尾流弛振响应.虽然下游圆柱3 和4 都呈现分离的涡激共振和尾流弛振响应,但是两者之间的振动幅值响应和涡脱频率仍有不同,所以四个圆柱之间的相互影响仍然存在.

当间距S/D=4.0 时,此时圆柱间距足够大,上游圆柱1 和2 不再受相邻圆柱的影响,即两圆柱彼此之间不再影响并且也不会受到下游圆柱3 和4 的影响,振动响应和单圆柱经典的涡激振动一样.由图9(b)和图9(c)可知,下游圆柱3 和4 尾流场的无量纲涡脱频率fs/fn响应也非常相似,都呈现4 个区域,在区间2.1≤Ur≤4.9 时,两圆柱的无量纲涡脱频率fs/fn都随着约化速度的增加近似沿着St≈0.13 线性变化,而在8.5≤Ur≤11.7 (下游圆柱3)或者8.5≤Ur≤11.0 (下游圆柱4)时,无量纲涡脱频率fs/fn没有明显的主频,此时两个圆柱振动都非常微弱.在5.5 11.7 (下游圆柱3) 或者Ur>11.0 (下游圆柱4)时,两圆柱的无量纲涡脱频率fs/fn又会出现多频响应(尾流弛振响应),因此在间距S/D=4.0 时下游圆柱3 和4 也会表现为分离的涡激共振和尾流弛振响应,并且两者之间的振动幅值和涡脱频率非常接近,所以此时4 个圆柱之间的相互影响已经非常小,类似于串列布置的双圆柱,即上游圆柱1 只影响下游圆柱3,上游圆柱2 只影响下游圆柱4,上游圆柱1 和2之间以及下游圆柱3 和4 之间都不会产生相互影响.

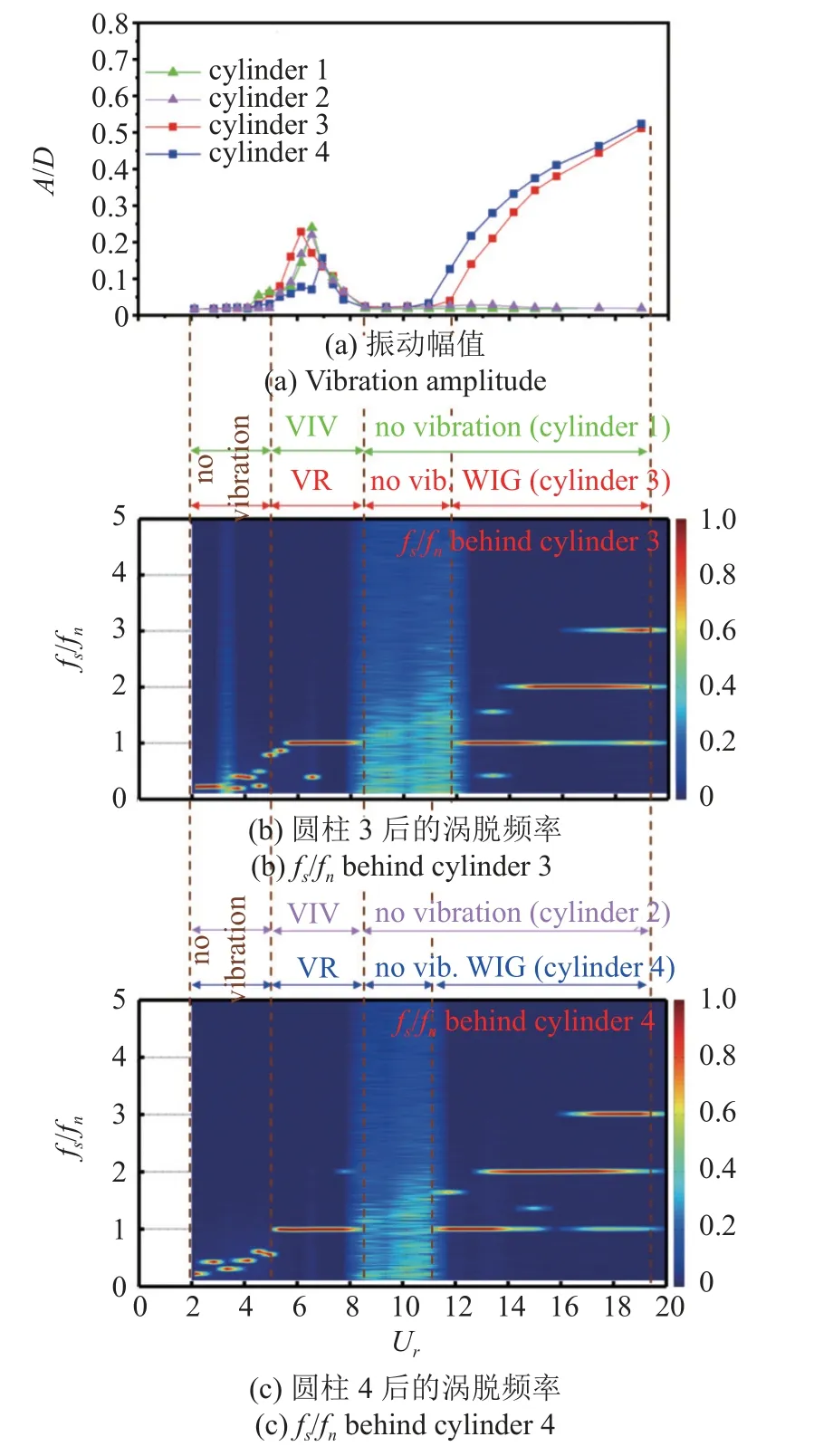
图9 S/D=4.0 时无量纲涡脱频率,(a)振动幅值,(b)圆柱3 后的涡脱频率,(c)圆柱4 后的涡脱频率Fig.9 Response of the normalized vortex shedding frequency fs/fn at S/D=4.0,(a)vibration amplitude,(b)fs/fn behind cylinder 3,(c)fs/fn behind cylinder 4

综上,结合串列、并列双圆柱的涡脱频率随间距的变化规律[13, 17]可以知道,上述布置方式和正方形布置四圆柱的涡脱频率响应存在着很多共同的特征.当间距较小时,正方形布置四圆柱和并列圆柱一样,其涡脱频率都呈现不对称的响应,这说明尾流场存在不对称性.当圆柱呈现涡激振动(上游圆柱)或者涡激共振(下游圆柱)时,涡脱频率fs在会明显地锁定在固有频率fn的1 倍谐频上,而随着约化速度的逐渐增大,圆柱开始呈现剧烈的类弛振响应(上游圆柱)或者尾流弛振响应(下游圆柱)时,涡脱频率fs会呈现明显的多倍谐频.如果涡激共振区和尾流弛振区是耦合在一起的(即耦合的涡激共振和尾流弛振响应)那么从1 倍谐频到多倍谐频也会连在一起而不发生中断现象,但是如果涡激共振区和尾流弛振区是分离开的(即分离的涡激共振和尾流弛振响应)那么从1 倍谐频到多倍谐频也会中断,并且在分离区fs/fn会随着约化速度的增加沿着St等于一个固定值线性变化或者没有明显的主频呈现无规律特性.

3.3 振动频率特性

圆柱模型的振动频率fo可以通过对测量的位移进行FFT 变换得到.为了简洁起见,现仅选取下游圆柱4 的结果来讨论本文正方形布置四圆柱模型的振动频率fo的特性,其余工况的响应结果和下游圆柱4 类似.图10 给出了间距S/D=1.5～4.0 时,模型的振动频率fo随约化速度Ur的变化规律,需要说明的是当圆柱振动幅值很弱的时候,位移经过FFT 变换后,无法捕捉到明显的主频,所以图10 中仅给出了圆柱振动明显时(锁定区间内)的振动频率.由图10可知,无论间距S/D如何变化,振动频率fo始终锁定在1 倍的固有频率fn上,和前述涡脱频率fs以及水中小质量阻尼比时振动频率fo(随着约化速度的变化而改变)[3]变化规律明显不同.

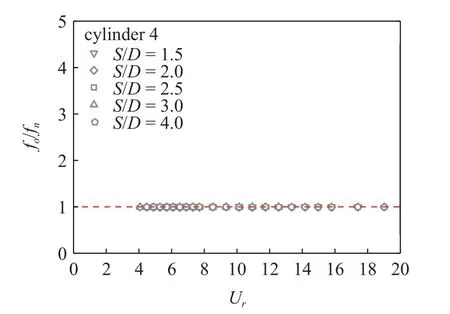
图10 下游圆柱4 在不同间距S/D 时的振动主频Fig.10 Dominant oscillation frequencies depending on S/D for cylinder 4

这种现象可以归因于有效附加质量mea的影响.本文风洞实验四圆柱模型的质量比分别为m*=345.3 (m=260.2 g,ma=0.75),344.9 (m=259.9 g,ma=0.75),345.1 (m=260.1 g,ma=0.75),345.0 (m=260.0 g,ma=0.75),其中ma(=CAρπD2l/4)为静止流场中的理想附加质量,CA为理想附加质量系数其值通常取为1.但是对于一个振动的结构,其附加质量会随之改变,可以称为有效附加质量mea(=CEAπρD2l/4),CEA为有效附加质量系数,在空气中非常小.

根据Khalak 等[27]的研究,圆柱模型的无量纲振动频率fo/fn可以定义为

由式(1)可知,m*越大,fo/fn越不容易改变,反之m*越小,fo/fn会发生很大变化.由于空气中圆柱模型m*很大,CEA远小于m*,因此CEA的变化对于式(1)中分母的影响可以忽略不计,这也正是本文风洞实验中大质量比条件下fo/fn会保持不变的原因.因此,正方形布置四圆柱的振动频率和质量比以及有效附加质量参数等密切相关.

4 结论

本文通过风洞实验系统地研究了雷诺数Re=3200～28900,间距比S/D=1.5～4.0 时正方形布置四圆柱的流致振动响应,通过对振动幅值、涡脱频率和振动频率等分析讨论,充分认识了大质量比条件下正方形布置四圆柱的干涉特性,探明了双圆柱结构和正方形布置四圆柱结构流致振动特性的关系.根据分析讨论结果,可以总结出以下结论.

(1)根据正方形布置四圆柱的振动幅值响应特征可知,当S/D≤2.0 时上游圆柱1 和2 都会呈现耦合的涡激振动和类弛振响应,下游圆柱3 和4 会呈现耦合的涡激共振和尾流弛振响应,但是由于间距较小,圆柱之间的相互干涉作用很强,因此上游圆柱1 和2 之间以及下游圆柱3 和4 之间的振动响应趋势呈现不对称性.当S/D≥ 2.5 时,上游圆柱1 和2 越来越接近单圆柱典型的涡激振动响应,下游圆柱3 和4 都表现为分离的涡激共振和尾流弛振响应,并且二者之间的振动幅值和响应区间也随着间距的增加逐渐接近.这表明随着间距的增加,圆柱之间的干涉作用越来越弱,正方形布置四圆柱中第一行的两个圆柱(圆柱1 和3) 和第二行的两个圆柱(圆柱2 和4)会逐渐类似于串列布置的双圆柱,即上游圆柱1 只影响下游圆柱3,上游圆柱2 只影响下游圆柱4.

(2)当圆柱呈现涡激振动(上游圆柱)或者涡激共振(下游圆柱)时,涡脱频率fs在会明显地锁定在固有频率fn的1 倍谐频上,而随着约化速度的逐渐增大,圆柱开始呈现剧烈的类弛振响应(上游圆柱) 或者尾流弛振响应(下游圆柱) 时,涡脱频率fs会呈现明显的多倍谐频.如果涡激振动区和尾流弛振区是耦合在一起的(即耦合的涡激振动和尾流弛振响应)那么从1 倍谐频到多倍谐频也会连在一起而不发生中断现象,但是如果涡激振动区和尾流弛振区是分离开的(即分离的涡激振动和尾流弛振响应)那么从1 倍谐频到多倍谐频也会中断,并且在分离区fs/fn会沿着St等于一个固定值线性变化或者没有明显的主频呈现无规律特性.而圆柱模型的振动频率和结构的质量比、有效附加质量等参数密切相关.由于本文风洞实验的质量比很大,有效附加质量远小于质量比,所以模型振动频率主频只能明显地锁定在1 倍的固有频率.

(3)结合双圆柱结构及正方形布置四圆柱结构的振动幅值响应结果,可以得出双圆柱系统、正方形布置四圆柱的振动幅值响应存在着共同的响应模式,双圆柱结构的一些动力学响应规律仍然适用于正方形布置四圆柱等多圆柱系统,这为揭示实际工程中更加复杂的多圆柱结构的动力学响应特征提供了有意义的参考和指导.