考虑螺杆转子表面质量与硬度的铣削参数优化*

林泽利 孙兴伟 杨赫然 刘 寅 赵泓荀

（①沈阳工业大学机械工程学院，辽宁 沈阳 110870；②辽宁省复杂曲面数控制造技术重点实验室，辽宁 沈阳 110870）

螺杆转子的重要性主要体现在螺杆机械的应用上。作为螺杆泵等重型螺杆机械的关键组成部件，其加工质量是影响螺杆机械设备的使用寿命以及其他使用性能的重要因素[1-2]。螺杆泵因其构造简单、流量脉动小等优点被广泛应用于石油开采、工程机械等领域。螺杆泵的工作过程中螺杆转子与定子之间存在相对运动，使两表面之间产生摩擦，表面越粗糙，接触面积就越小，磨损就越快，螺杆转子的耐磨性就越差；硬度对螺杆转子的耐磨性也有一定影响，硬度的提高，在一定程度上可以提高螺杆转子的耐磨性。因此，提高螺杆转子的表面质量和硬度，延长螺杆转子的使用寿命变得尤为重要[3]。

多年来一直有学者不断对工件表面粗糙度和硬度进行研究。豆卫涛等[4]、王运等[5]均通过车削试验，分析了工艺参数对零件的表面粗糙度的影响规律。Zhang H P 等[6]进行了300M 超强度钢的高速车削试验，分析了影响表面粗糙度的各种因素的先后顺序，并正交切削实验，得到了影响表面粗糙度的主要和次要影响因素。在硬度研究方面，张昌明等[7]研究了铣削工艺参数对A100 合金钢的表面显微硬度的影响，通过极差分析得出了工艺参数对硬度影响程度的大小顺序。于英钊等[8]针对AISI 高强度钢经过高速干铣削加工后的表面加工硬化进行了研究。Wang C G 等[9]对侧铣加工ZK61M 镁合金板材的表面硬度进行了简要分析，发现铣削温度对加工表面的硬度起主要作用。机加工后工件的表面质量对其各种性能都有一定影响。

本文以多头螺杆转子为研究对象，通过螺杆转子外包络铣削加工试验，对螺杆转子的表面粗糙度和硬度进行研究，结合多目标原子轨道搜索优化算法，对工艺参数进行优化，寻找最优参数组合，为提高螺杆转子的表面加工质量和服役可靠性提供支撑。

1 外包络铣削加工原理

螺杆转子外包络铣削加工原理如图1 所示。加工前，调整盘铣刀刀盘，使刀盘轴线与工件轴线形成夹角，该夹角大小等于螺杆转子的螺旋角[10]。依靠盘铣刀的旋转、盘铣刀沿工件轴向的进给、盘铣刀沿工件径向的往复进给和工件的旋转完成螺杆转子的加工。图1 中，盘铣刀的转速为n，刀具沿工件轴向的进给运动为间歇进给运动，工件每旋转一周完成一个端面轮廓的加工，一个端面轮廓加工结束，刀具沿工件轴向进给一次，进行下一个端面轮廓的加工，间歇进给量为f。刀具沿工件径向往复进给运动和工件自身旋转运动需要联动配合，才能完成螺杆转子的加工，往复进给速度和工件旋转速度通过加工倍率F进行调整。

2 螺杆转子加工试验

2.1 试验加工设备

螺杆转子的铣削加工试验用数控螺杆铣床LXK300G，如图2 所示。加工刀具为盘铣刀，刀盘直径290 mm，配备24 个菱形刀片，刀片材料为硬质合金，切削刃长16 mm。试件为圆柱形棒料，直径100 mm，长度为1 200 mm，材料为45#钢，其化学成分及物理属性分别见表1 和表2。

表1 45#钢化学成分（%）

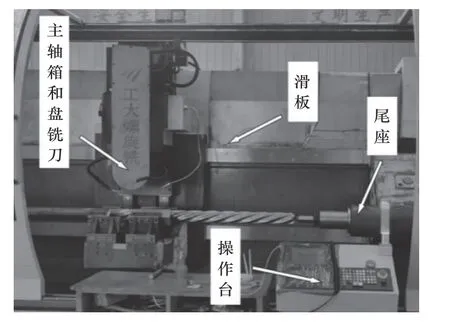
图2 螺杆转子加工现场

2.2 试验方案设计与测量结果

为研究外包络铣削工艺参数对螺杆转子的表面粗糙度值和显微硬度值的影响，以主轴转速n、间歇进给量f、加工倍率F作为影响因素，设计了三因素五水平正交试验，根据实际加工条件确定工艺参数的各水平指标，见表3。试验加工完成后，使用TR200 便携式粗糙度仪和显微维氏硬度计进行表面粗糙度和显微硬度的测量，如图3 所示。25 组正交试验方案及测量结果见表4。

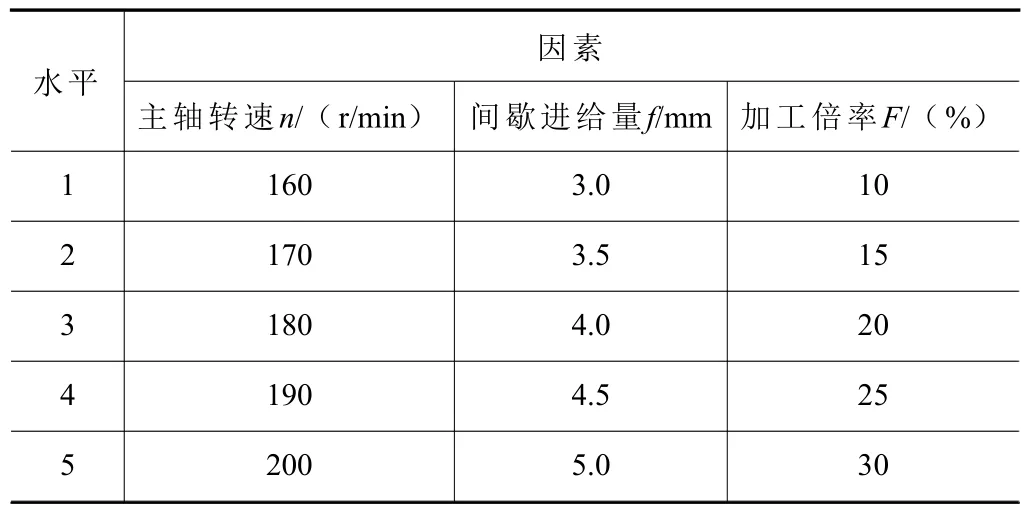
表3 正交试验因素水平表

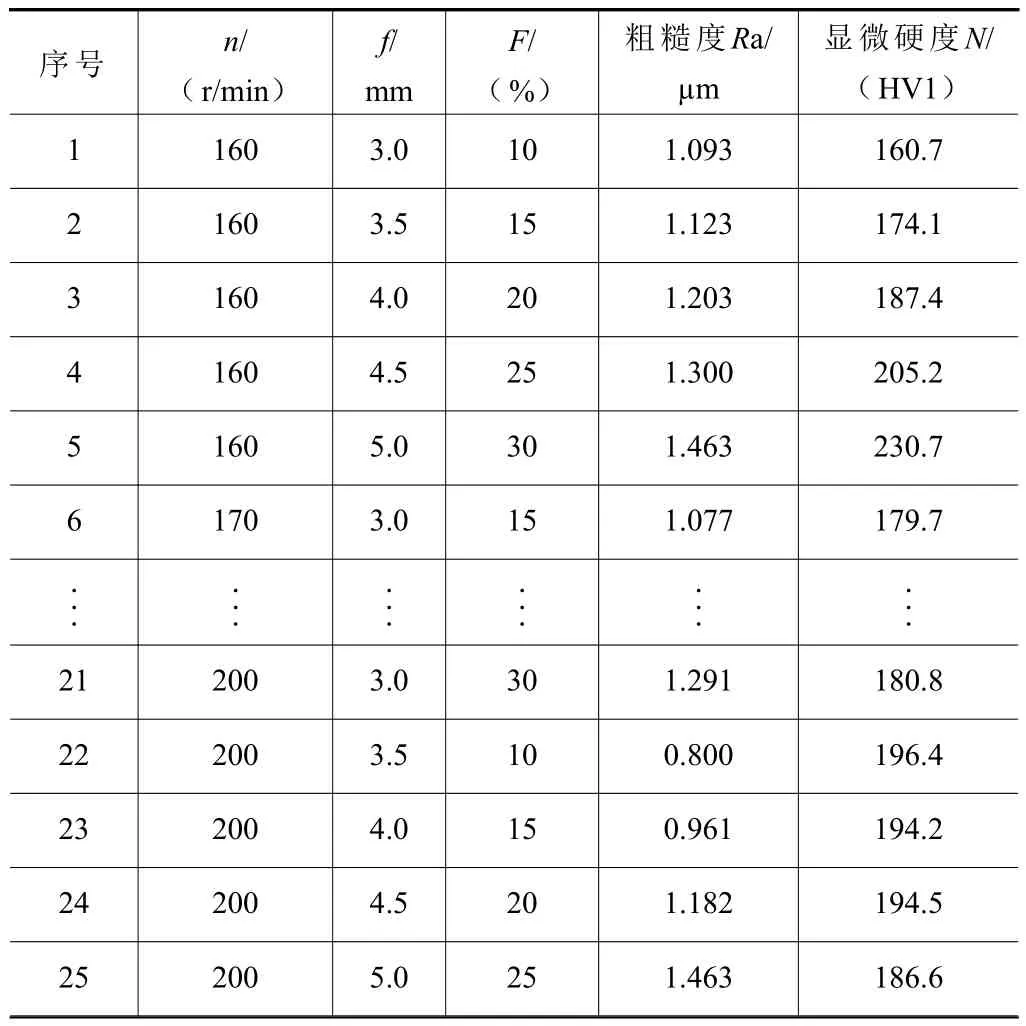
表4 正交试验方案及结果

图3 试验结果测量

3 试验结果分析及回归模型建立

对表面粗糙度和显微硬度数据进行方差分析，建立回归方程。方差分析的作用是分析工艺参数及工艺参数的交互项对表面粗糙度值和显微硬度值影响的显著性，方差分析在0.05 显著性水平下进行[11]。表5 是表面粗糙度值Ra 的方差分析结果，可以判断工艺参数（n、F）、平方项（F×F）、交互项（n×f、n×F）对表面粗糙度值有显著影响，因为这些项的P值均小于0.05。工艺参数对表面粗糙度的影响程度大小依次为：加工倍率、间歇进给量、主轴转速。表6 是显微硬度N的方差分析结果，可以分析出工艺参数（f）、平方项（n×n、f×f、F×F）、交互项（n×f、n×F）对显微硬度N有显著影响，因为这些项的P值均小于0.05。工艺参数对显微硬度的影响程度大小依次为：间歇进给量、加工倍率、主轴转速。

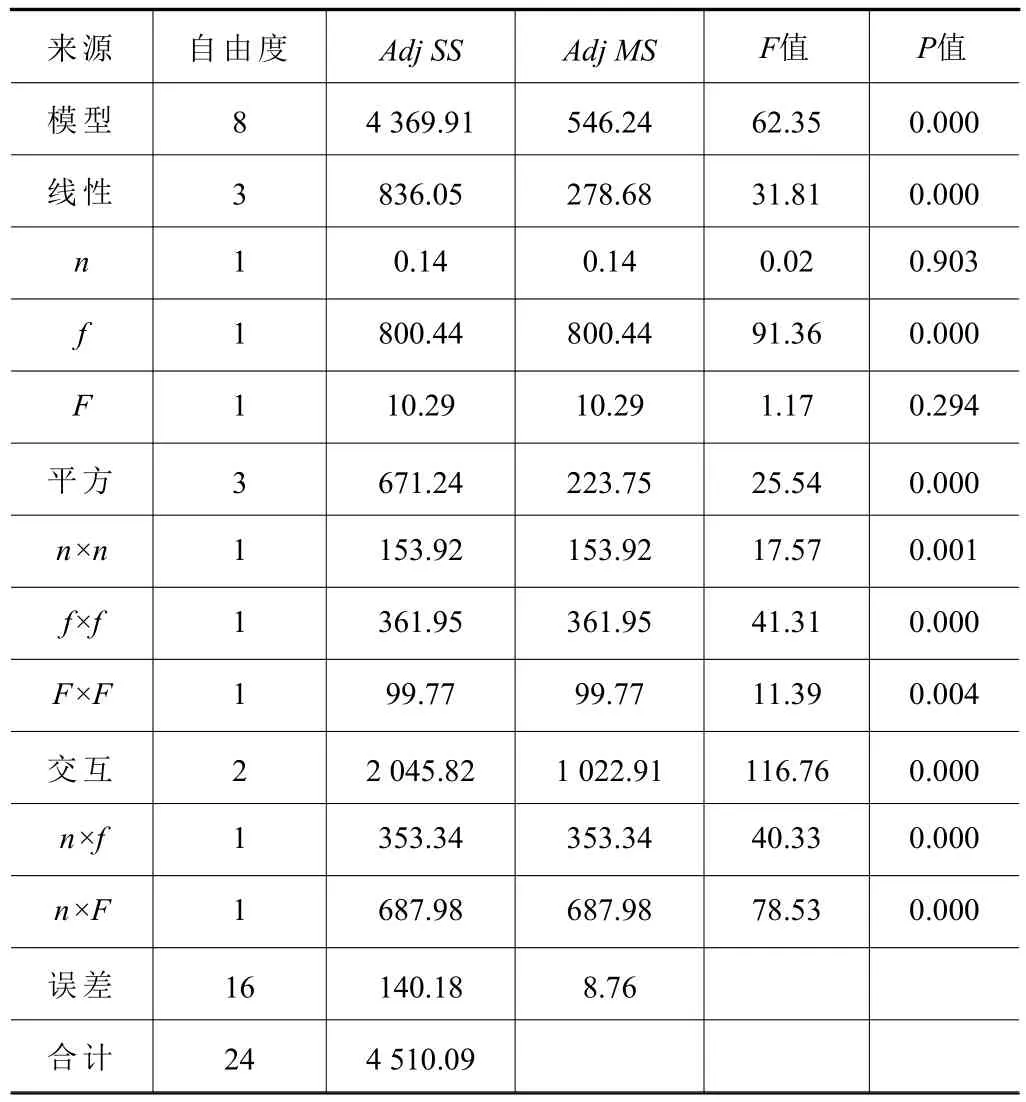
表6 N 方差分析结果

建立表面粗糙度值Ra 和显微硬度值N与工艺参数之间关系的数学回归模型，分别见式（1）和式（2）。

通过对上述数学模型分析可知，表面粗糙度值Ra 数学模型的R-sq为96.11%，R-sq（调整）为94.17%，R-sq（预测）为90.91%；显微硬度N数学模型的R-sq为96.89%，R-sq（调整）为95.34%，Rsq（预测）为90.13%，说明上述数学模型的拟合程度良好，可用于预测给定的工艺参数对应的粗糙度值和显微硬度值。

4 基于多目标原子轨道搜索优化算法工艺参数寻优

4.1 原子轨道搜索优化算法

原子轨道搜索（atomic orbital search，AOS）算法是2021 年Azizi M 提出的，其灵感来自于量子原子理论所考虑的电子密度构型和原子对能量的吸收或发射的基本原理[12]。该算法具有较强的全局搜索能力，能够避免陷入局部最优，同时也具有较快的搜索速度。在该算法中，每个电子代表一个可行解X，搜索空间为围绕原子核的电子云，其物理模型可分成不同半径的薄球壳层。

其中：i=1,2,···,m；j=1,2,···,d；m为候选解数量；d为问题维度。电子初始位置可由式（4）确定：

在每层中最佳目标函数值的候选解为该层中最低能级的电子。为了从数学上表示光子对原子核周围电子的作用，在(0,1)范围内为每个电子生成一个均匀分布的随机数φ。此外，光子速率PR被确定为光子对电子作用的概率的参数。如果φ＞PR，光子对电子的作用是可能的，需要再判断光子的发射和吸收，如果，则考虑光子的发射，候选解位置更新方式见式（5）；如果，则考虑光子的吸收，候选解的位置更新方式见式（6）。如果φ＜PR，光子对电子的作用是不可能的，不同层电子的运动可能是其他因素导致的，候选解的位置更新方式见式（7）。

4.2 确定优化目标

表面粗糙度和显微硬度是影响螺杆转子使用性能的两个重要因素[13]。表面粗糙度值越小表明工件的表面质量越好，故第一个优化目标函数见式（8）；显微硬度的增加可以提高转子的耐磨性，故第二个优化目标函数见式（9）。

通过式（1）、式（2）、式（8）、式（9）可以看出优化目标主要与工艺参数有关，故将主轴转速、间歇进给量、加工倍率设置为优化变量。优化变量的求解范围根据实际加工条件设定，本次将正交试验的参数范围作为优化变量的约束条件，具体如下：

（1）主轴转速：160～200 r/min。

（2）间歇进给量：3～5 mm。

（3）加工倍率：10%～30%。

将表面粗糙度值和显微硬度作为优化算法的目标，多目标优化流程如图4 所示。

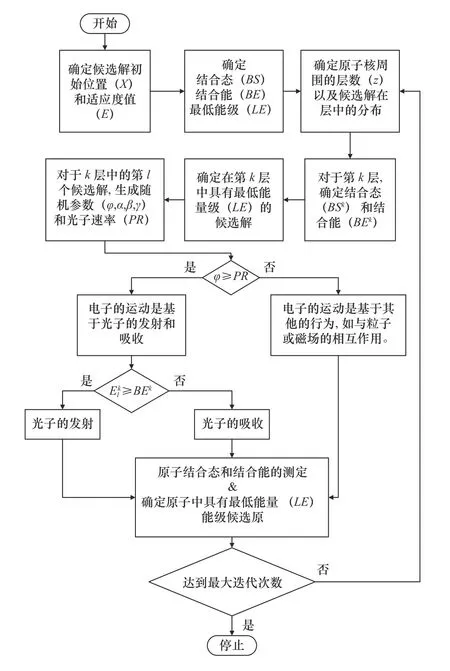
图4 多目标优化流程图

由于该算法具有较强的搜索能力和较快的搜索速度，故设置迭代次数为100。当完成100 次迭代过程后多目标优化算法停止迭代，可以得到Pareto解集。

4.3 Pareto 解集选优

采用多目标优化算法得到的一系列非支配解，即为Pareto 最优解集[14]。优化结果要从该解集中选取，通常的选择方式是根据经验选择，但是这样选择随机性较大。因此，采用基于模糊集合理论在Pareto 最优解集中选取最优解[15]。

定义支配函数 ξr，第r个解的支配值为

式中：h为解的数量，g为优化目标个数。

根据支配函数 ξr计算公式，可以计算Pareto 解集中所有解的支配值，计算结果能够很好地反映该解的综合性能，数值越大说明解的性能越好，故选择支配值最大的解作为最优解。

4.4 优化结果分析

根据式（11）计算出Pareto 解集中所有解的支配值，结果如图5 所示。

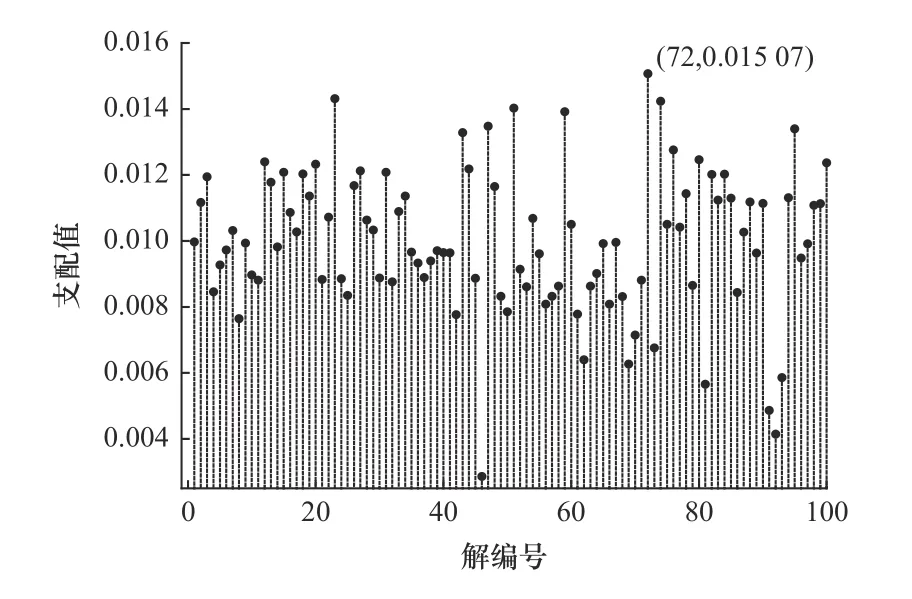
图5 最优解集的支配值

从图5 中可以看出，72 号解的支配值最大，说明该解的综合性能最好，故将其确定为最优解，对应工艺参数优化前后见表7。

表7 设计变量优化结果

采用优化前的工艺参数进行试验加工，得到的表面粗糙度值为1.102 μm，显微硬度为188.2 HV1。根据实际加工与试验设备条件情况，无法精确达到最优工艺参数，在保证其他加工条件不变的情况下，需要对寻优得到的工艺参数进行调整。调整后主轴转速为191 r/min，间歇进给量为3.1 mm，加工倍率为15%。使用最优参数组合进行试验，得到工件表面粗糙度值为0.913 μm，显微硬度为202.5 HV1，优化后表面粗糙度值降低了17.15%，显微硬度提高了7.60%，使螺杆转子加工后的表面质量得到提高。

5 结语

本文针对螺杆转子的表面粗糙度和硬度进行研究，通过外包络铣削正交试验，得到结论如下。

（1）工艺参数对表面粗糙度影响的主次顺序依次为：加工倍率、间歇进给量、主轴转速。对显微硬度影响的主次顺序依次为：间歇进给量、加工倍率、主轴转速。根据试验数据建立表面粗糙度和显微硬度的数学回归建模，通过分析表明模型拟合程度良好，可用于工艺参数寻优。

（2）利用多目标原子轨道搜索优化算法进行工艺参数优化，得到最优工艺参数组合为：主轴转速为191 r/min，间歇进给量为3.1 mm，加工倍率为15%。采用该参数组合进行铣削加工试验，与优化前进行对比，发现螺杆转子的表面粗糙度值降低了17.15%，显微硬度提高了7.60%，使得螺杆转子的加工质量得到提高。