“动”中求“静”，“动”“静”互化

袁媛

摘要：在初中平面几何的学习中，要运用运动变化的思路研究图形，让静止的几何图形“动”起来，化抽象为具体，让变化的图形形象直观地揭示出恒定不变的几何规律，把相关的知识点串联起来，这样有助于提高分析问题和解决问题的能力.本文中结合中考试题，对常见的动态几何类题型的解题思路与方法进行了初步探索.

关键词：“动”“静”转化；动“点”类问题；动“线”类问题；动“图”类问题

马克思主义哲学告诉我们，运动是绝对的，静止是相对的.在几何的学习过程中，我们发现“静”只是“动”的瞬间，是运动的一种特殊形式，“动”与“静”是可以相互转化的.如果能让静止的几何图形“动”起来，就可以帮助学生加深对图形概念的准确理解，探索图形的性质.教师可以用动态图形创设富有启发性的教学情境，引发学生对问题的讨论与思考；还可以通过动态图形让学生体验数学实验成功的乐趣.更重要的是，动态的几何图形能够把与几何、代数相关的知识联系起来，其中蕴含着动静结合、数形结合的思想方法，能够在运动变化中发展学生的空间想象能力，不断提高学生综合分析、解决问题的能力.

在初中几何教学中，与动态图形有关的问题主要有以下几类.

1 动“点”类问题

动点问题是中考数学中最常见的题型，涉及面非常广泛.解决动点类问题的思路是化动为静，以相对静止的瞬间去寻求量与量之間的关系.

解析：如图2所示，在矩形ABCD中，设AB=2a，BC=3a，运动时间为t，则CD=AB=2a，AD=BC=3a，BN=v2t，AM=v1t.在运动过程中，将四边形MABN沿MN翻折，得到四边形MA′B′N，所以B′N=BN=v2t，A′M=AM=v1t.若在某一时刻，点B的对应点B′恰好在CD的中点重合，则DB′=B′C=a.在Rt△B′CN中，∠C=90°，

思路与方法：本题考查矩形背景下的动点问题，通过动态图形，将矩形的性质、对称性质、中点性质、三角形相似、全等的判定与性质、勾股定理及翻折的运动形式等知识点联系起来.熟练掌握相关性质及三角形全等的判定定理，利用翻折及中点性质，根据三角形全等的性质求出相应线段的长是解题的重要方法.

2 动“线”类问题

动线类问题的特点很明显，动线在运动过程中可能会出现多种情况，尽管情况不同，但解题的思路是一致的，那就是“以静制动”，通过特殊的静止状态去寻找量之间的关系.

例2 （2022年江苏省盐城市中考第14题）如图3，在矩形ABCD中，AB=2BC=2，将线段AB绕点A按逆时针方向旋转，使得点B落在边CD上的点B′处，线段AB扫过的面积为.

解析：[HTF]由AB=2BC=2，得BC=1，所以AD=BC=1.因为将线段AB绕点A按逆时针方向旋转，所以AB′=AB=2.

思路与方法：首先由动线AB旋转的性质可得AB′=AB=2，再由锐角三角函数可求出∠DAB′=60°，进而求出∠BAB′，最后根据扇形面积公式即可获解.本题考查了旋转的性质、矩形的性质、扇形的面积公式、锐角三角函数等相关知识点.会观察和分析动态图形，灵活运用相关性质是解题的关键.

3 动“图”类问题

动图类问题常常结合图形的平移、旋转、翻折等变换，提出相关问题.解题的思路主要是从寻找图形运动的特殊情况中打开，进而灵活运用相关几何知识（如平行四边形的性质、切线的性质、圆的有关知识、锐角三角函数、直角三角形等）解决问题.

例3 （2022年江苏省苏州市中考全真模拟试题第18题）在△ABC中，AB=BC=6，∠ABC=90°，点D在AC上，且AD=22，E是射线AB上一动点，连接ED并将ED绕着点E旋转60°得线段EF，当点F恰好落在直线AC上时，可求得AE的长等于.

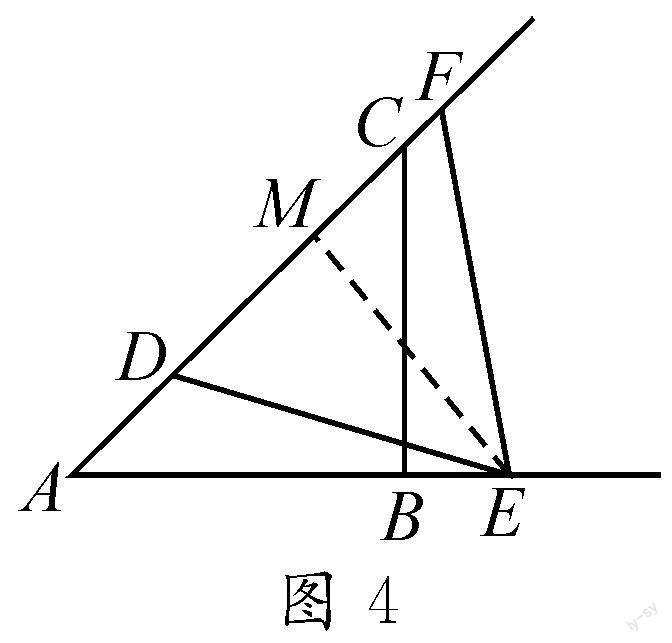
解析：第一种情况.当ED顺时针旋转60°得到EF时，如图4，过点E作EM⊥AC于点M.因为AB=BC=6，∠ABC=90°，所以△ABC是等腰直角三角形，于是∠A=45°.根据旋转的性质，可得∠DEF=60°，EF=ED，所以△DEF是等边三角形，故∠DEM=30°.设DM=x，则DE=2x，

第二种情况：当ED逆时针旋转60°得到EF时，如图5，作EM⊥AC交AC于点M.

思路与方法：首先要考虑到图形顺、逆两种旋转情况，根据旋转的性质可知△DEF是等边三角形，过点E作EM⊥AC，又可证得△AEM是等腰直角三角形，再设DM=x，利用勾股定理便可求出x的值，最后利用勾股定理即可求出AE的长度.本题考查了图形旋转的性质、等边三角形的判定与性质、勾股定理等知识点.能够根据题意，按照ED顺时针旋转与逆时针旋转两种情况，分别画出动态图形进行分类解析是解题的关键.

综上所述，解决动态几何问题的基本思路是：把握运动规律，寻求运动中的特殊位置，在“动”中求“静”，在“静”中探求“动”的普遍规律.在具体解题过程中，要用运动与变化的眼光去观察和研究图形，把握图形运动与变化的全过程，找出其中的等量关系和变量关系，并要特别关注一些不变量和不变关系或特殊关系.在解答动态几何类题型时，经常要用到数形结合思想、分类思想、转化思想和方程思想等重要的思想方法.