大功率履带越野车用液力变矩器循环工况构建
闫清东,杜艺舟,刘 城,3,魏 巍,4
(1.北京理工大学 机械与车辆学院,北京 100081; 2.北京理工大学 前沿技术研究院,济南 250300; 3.车辆传动重点实验室(北京理工大学),北京 100081; 4.北京理工大学 重庆创新中心,重庆 401135)
液力变矩器是一种柔性传动流体机械,其具有可靠性高、自适应性强、隔离振动冲击等特点,在特种车辆、工程机械、农业机械和汽车等领域被广泛应用[1]。作为由发动机向变速机构传递动力的关键部件,液力变矩器的可靠性与耐久性检验是评价其质量的关键[2-3],而试验过程的工况设定对试验结果的可信度和参考价值有决定性影响[4-5]。
目前国内所采用的液力变矩器可靠性检验标准为2007年颁布的机械行业标准JB/T 10762—2007《液力变矩器可靠性试验方法》[6]。该方法利用连续高负荷试验(速比i保持0.3)和动负荷冲击试验(零速-空载周期)代替实车复杂运行工况,无法反应实车运行过程中液力变矩器工作状态,且仅能对液力变矩器牵引性能作考核。为了更加科学完善地设计液力变矩器可靠性试验,需要构建能够反映液力变矩器实车条件下运行特征的试验循环工况,研究叶轮在复杂道路载荷条件下的运行态势,以满足车辆对高可靠性液力变矩器试验的需求[7]。
针对城市道路车辆的行驶工况已有较多研究,苗强等[8]以济南市公交车为对象,利用聚类和马尔科夫链方法构建了其典型行驶工况。Kaymaz等[9]对土耳其首都伊斯坦布尔数年的车辆工况数据进行分析,首次通过比例分层抽样技术构建了快速公交系统的循环工况,其成果为混合动力公交车的排放和能源测试提供了合理依据。Günther等[10]开发了一整套行驶工况生成工具,并用其生成了德国汉堡市公交车行驶工况。上述方法均为对单一维度车速循环工况构建方法进行研究,但由于液力变矩器工况由泵轮转速、涡轮转速两个维度表征,构建其循环工况时需要将速比分布、闭解锁切换等更多因素纳入考量。
本文基于大功率越野车辆的运行工况数据,提出了从泵轮转速、涡轮转速两个维度构建包含牵引、闭锁两种模式的大功率履带式越野车辆循环工况的方法,为越野车辆用液力变矩器可靠性/耐久性考核提供数据支撑。
1 实车运行数据统计与降维
1.1 数据分段
本文数据来源于装备液力机械综合传动装置的履带越野车辆,该型车用液力变矩器为带闭锁离合器的综合式液力变矩器。工况数据涵盖高原、热区、寒区、越野路面、铺装路面等多种典型行驶环境及场景。以闭锁油压(1.53 MPa)为界将总体数据切片,得到多个非闭锁工况数据片段7 101个,闭锁工况片段7 314个,统计液力变矩器闭锁、牵引、反传工况的时长占比如图1所示。
图1中由于非道路履带车辆大部分处于越野工况中,对动力需求较高,总体工况中的变矩牵引部分占比最高,闭锁工况占比在45.00%左右,反传工况占比达8.55%。对数据中液力变矩器非闭锁工况数据进行统计如图2所示。
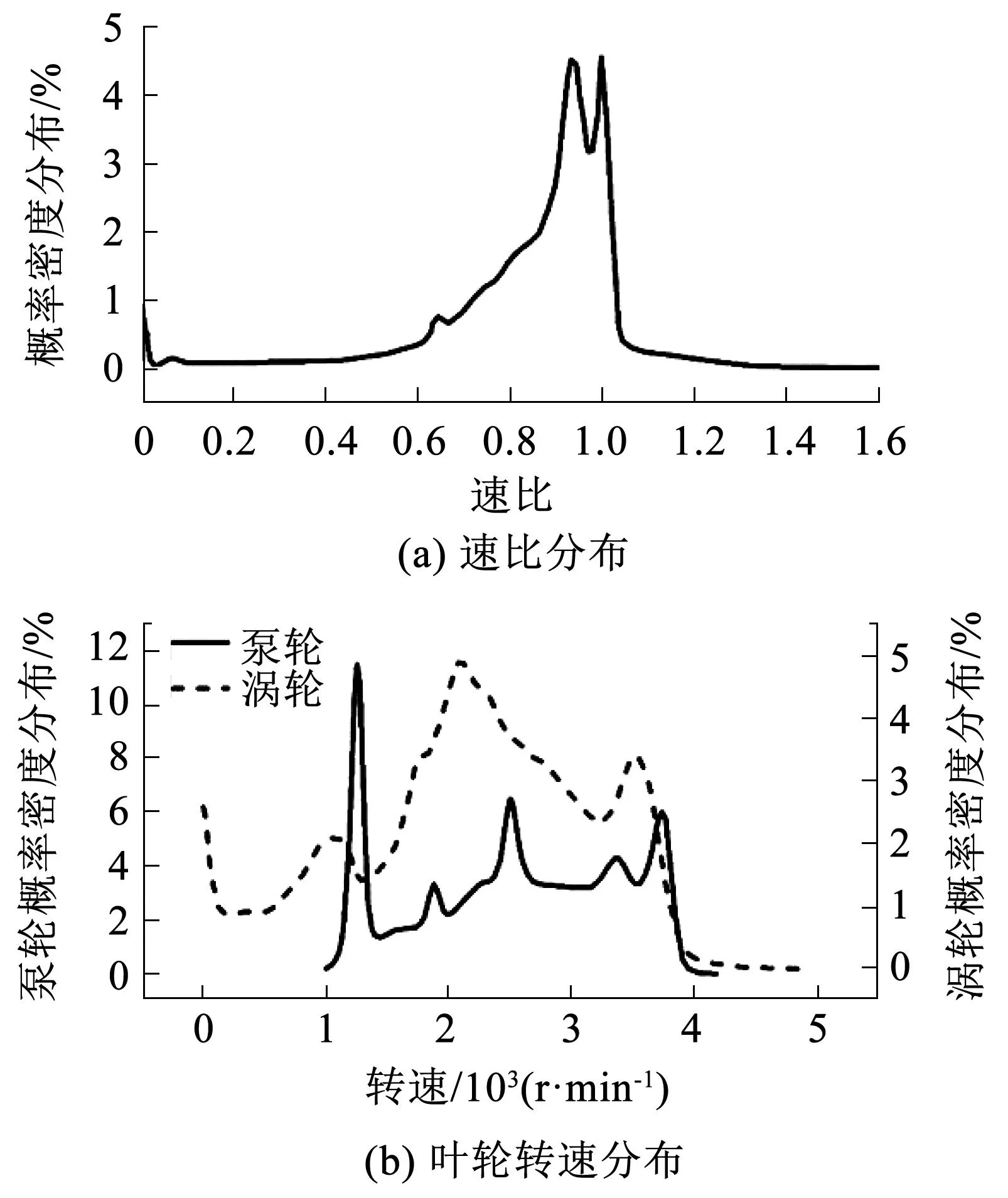
图2 数据概览Fig.2 Data overview
由图2可知,牵引工况下,液力变矩器速比概率密度分布总体上随着速比的升高而升高,同时i=1附近处存在明显下凹。
1.2 特征参数选取与统计
提出了包括平均速比、平均泵轮转速等22个参数,表征液力变矩器在实车运行过程中的主要运行特性,统计结果见表1、2。

表1 实车数据液力变矩器统计特征参数Tab.1 Statistical characteristic parameters of hydraulic torque converter with real vehicle data

表2 实车数据液力变矩器比例特征参数Tab.2 Proportional characteristic parameters of hydraulic torque converter with real vehicle data
1)平均速比、速比标准差、最高泵轮转速、泵轮平均转速、泵轮转速标准差。反映了变矩器速比、泵轮转速观测值的相对集中位置及离散程度。
2)速比、泵轮转速分布。反映了变矩器在不同工况、不同泵轮转速下的占比。
3)泵轮、涡轮的角加速度正、负均值。二者分别为正、负时的平均水平,反映叶轮在不同加减速状态下的角加速度大小,即车辆和发动机动态运行情况。
由表1、2可知,由于闭锁及高速比工况占比过半,液力变矩器平均速比达到0.89,同时液力变矩器平均泵轮转速和平均涡轮转速均较高,表明动力传动系统输出功率较大,而速比为0.60~1.00工况占绝大部分,表明非闭锁条件下,液力变矩器运行过程中大部分处于高效区工况。
2 特征参数的主成分分析及降维
提出的22个特征参数可对液力变矩器运行工况进行比详细解析,但难以根据如此多的维度进行工况构建,需要对工况数据进行降维分析。主成分分析法(PCA)是大型数据集规约统计的有效方法,它的目标是找出初始特征的几个方差最大的正交线性组合[11-13],以使用更少数据维度描述更多特性。
2.1 特征参数矩阵的标准化处理
由于不同特征参数的量纲和尺度不同,需要将特征参数矩阵进行标准化处理。
假设原数据集共划分为m个片段,并选取求解了n个特征参数,其m×n的结果矩阵A为
(1)
式中xij为第i个片段的第j个特征参数。
其标准化过程及标准化结果矩阵A′为:
(2)
(3)
式中,i=1,2,3,…,m,j=1,2,3,…,n。
2.2 相关系数矩阵
求得n个特征参数的相关系数n×n矩阵B及其来源为:

(4)
2.3 特征值与特征向量
根据特征值方程|λI-B|=0求得相关系数矩阵B的n个特征值及其特征向量,并计算累计贡献度见表3。
各个主成分的贡献度及累计贡献度(见表3),与传统的仅用车速作为单一维度的整车行驶工况不同,液力变矩器工作状态的确定至少需要泵轮转速和涡轮转速两个参数,特征值维度难以集中,取阈值为80%。因此选取前8个主成分进行数据表征,记录主成分特征值对应的特征向量所组成的矩阵为C。
2.4 用主成分表征全部特征参数
利用特征值与特征向量得到的矩阵C可将m个变矩器工作片段在特征参数空间内的n=22维坐标降维至t=8维空间,降维过程为
(5)
所得m×t矩阵D即为m个工况片段在降维后的8维空间中的坐标。
通过降维,将22维的工况状态空间精简至8维状态空间,且每个维度均为多个特征参数的不同线性组合,极大精简了后续分析循环工况构建流程。
3 工况片段的聚类分析
3.1 非闭锁工况片段的聚类分析
为识别、选取出典型工况片段,利用K均值聚类法对非闭锁工况片段进行聚类分析处理,将数据集划分为不同类别,使每个簇内部尽可能紧凑,簇之间尽可能独立[14-15],再从各簇内选取典型工况片段以进行循环工况的构建。
K均值聚类的准确性主要受K值的影响,目前使用较多的选取指标有以下3项。
1)全体样本的聚类误差平方和SSE(sum of squares due to error)。其含义为簇数取K时每个点到其属类中心距离平方之和。
(6)
式中SSSE即为本文样本的聚类误差平方和。
2)聚类结果的平均轮廓系数SC(silhouette coefficient)。该值越大表示聚类结果的内部越紧密,该值越小表示不同的簇越相似,聚类犯错的可能性越大[14]。
(7)
式中SSC即为本文样本的平均轮廓系数。
3)CH分数(分散率calinski-harabasz score)。该值越大,说明分类结果的类间差异性越大,各个簇彼此分布越分散。
(8)
式中:SCH为本文样本的分散率,k为K可能取得的所有值,C为聚类集合,c为对应集合的均值点,x为样本坐标。
合理的K值应该使SSE减小速度尽可能趋于稳定的同时使SC和CH分数尽可能大,绘制K∈(1,10)的指标值如图3所示。
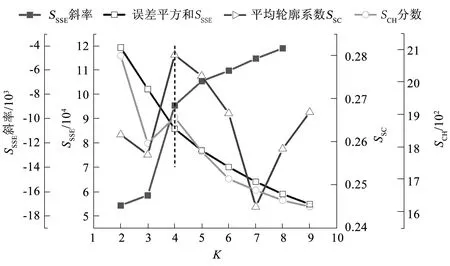
图3 K值的选取Fig.3 Selection of K value
由图3中分析可知,对于误差平方和SSE而言,当K为2、3时SSSE值较高并随K增加迅速衰减,当K>4时,其曲线变化速度放缓;SSC在K=4时达到最大值,明显高于其他各点;SCH在K=2和K=4取极大值,但仅将片段划分为两类难以描述其特征。故综上所述,当K取4时,可以兼顾3项指标,从而使K均值聚类的效果最好。
3.2 聚类分析结果
利用Sklearn库对液力变矩器工况数据片段进行K均值聚类分析,分析结果如图4所示。
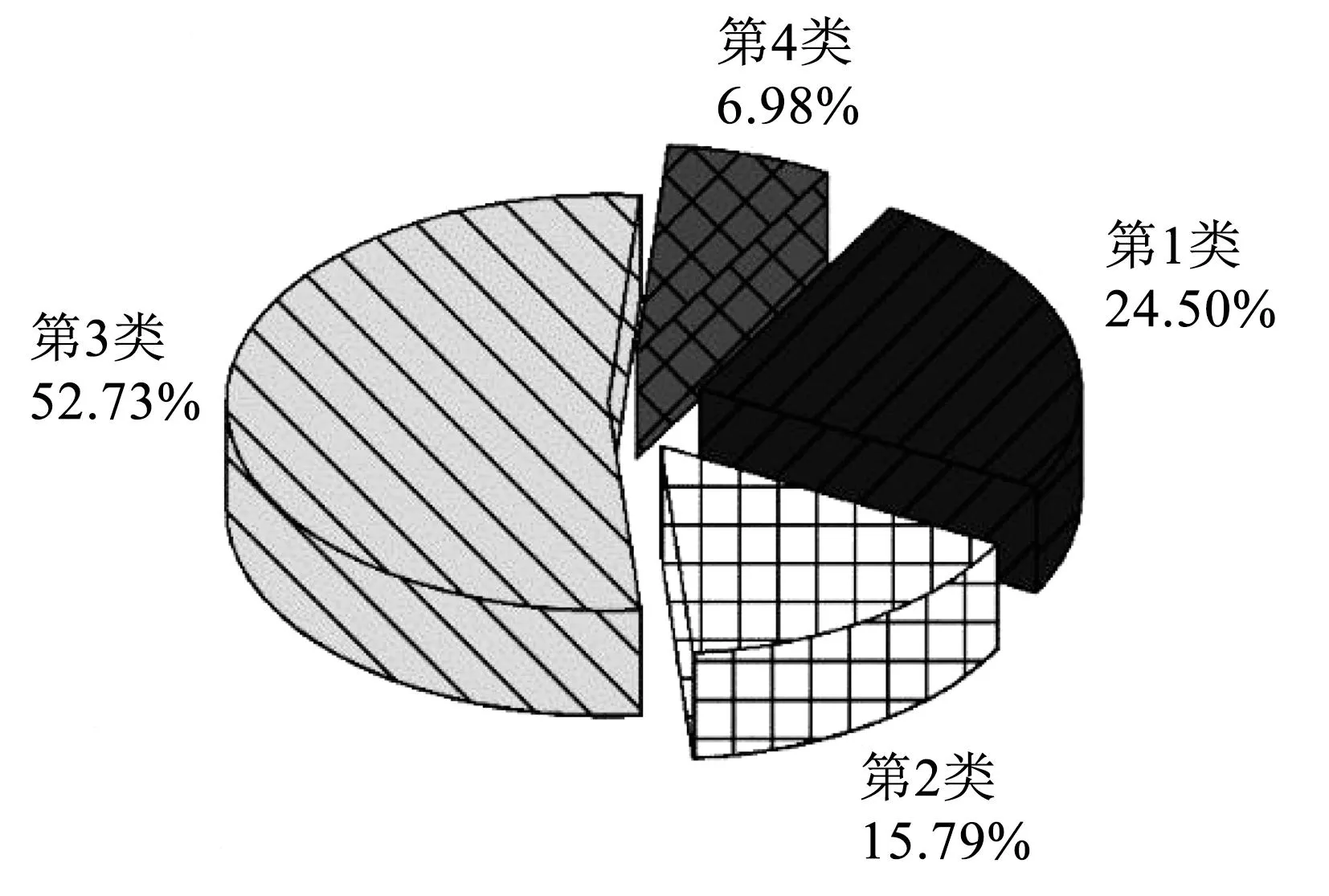
图4 各类工况片段在总体数据中的占比Fig.4 Percentage of each type of working condition segment
根据图4所示,除闭锁工况外,非闭锁工况中第3类工况总时长占比最高,为52.73%;第1类工况其次,为24.50%;第4类工况的占比最少,为6.98%。
绘制样本点在前三维度空间的投影点如图5所示。由图5可知,聚类分析将工况数据点在各主成分上进行了识别和聚类,其中第3类样本分布较为离散,边缘分布较为稀疏;第2、4类样本分布较为集中,边缘点较少;整个样本群体中未发现明显的离群点。

图5 片段特征值点前三维投影Fig.5 Projection of top three dimensions of segment feature values
同时统计速比区间和类别分布如图6所示,起动工况全部在第3类片段中,且速比0.30~0.60也以第3段为主,因此第3类片段表示起动、加速等工况;第1类片段中速比大于1.00的反传工况比例最高为主,第4类工况在速比0.60~1.00、1.00+两个区间均占比较高(43.9%、38.6%),说明第1、4类片段以高效区工况为主;第2类片段主要分布在速比0.30~1.00液力工况,主要为牵引工况,反传工况仅占4.3%。

图6 各类工况与不同速比区间内占比Fig.6 Proportion of each type of working condition within different speed ratio ranges
通过聚类分析,将实车运行中非闭锁工况片段聚为4类,且通过8维空间内的欧式距离给出了每个片段的代表性评估,获悉了液力变矩器的典型工作状态,为循环工况构建提供了数据支撑。
4 循环工况合成与优化
本文提取各类工况中距均值中心点欧氏距离前5%的片段作为典型片段,并对典型片段的选取和排列进行优化,以使构建的循环工况能够最大程度还原实车运行工况统计结果且便于试验测试。
4.1 片段连接及平滑方法
为使片段连接平滑、合理,提出以下两点原则:
1)对能够溯源重连的片段优先组合。由于闭锁片段与牵引片段均来自原始数据,故进行闭锁片段选择时,优先选择同当前牵引片段时序相连的工况片段,从而减少不必要的平滑连接,充分利用原始数据。
2)对独立的、无法直接连接的片段,利用加窗重构的方法[16]进行平滑连接。加窗重构是将独立的两段信号分别用窗函数进行点乘叠加后再连接。汉宁窗(式(9))可在光滑连接信号的同时避免引入与原始数据特征无关的极值载荷。
(9)
式中M为窗函数宽度,其取值与原始数据采样频率有关。
加窗重构的数学过程如下:
1)连接处序列z计算公式为
(10)
2)重构后连接点前、连接处、连接点后时序数据为
(11)
式中:i为连接处序列下标,M为窗函数的长度,x、z、y分别为连接点前、连接处、连接点后数据序列。
加窗重构平滑连接的效果如图7所示。图7中,虚线在连接点前处于下降趋势且曲线由凸转凹,实线在连接点后亦处于下降趋势且连接点转速值高出虚线约400 r·min-1,重构后连接可见的局部极值并非因为平滑连接引入,而是保留的两段转速曲线连接处局部特征。
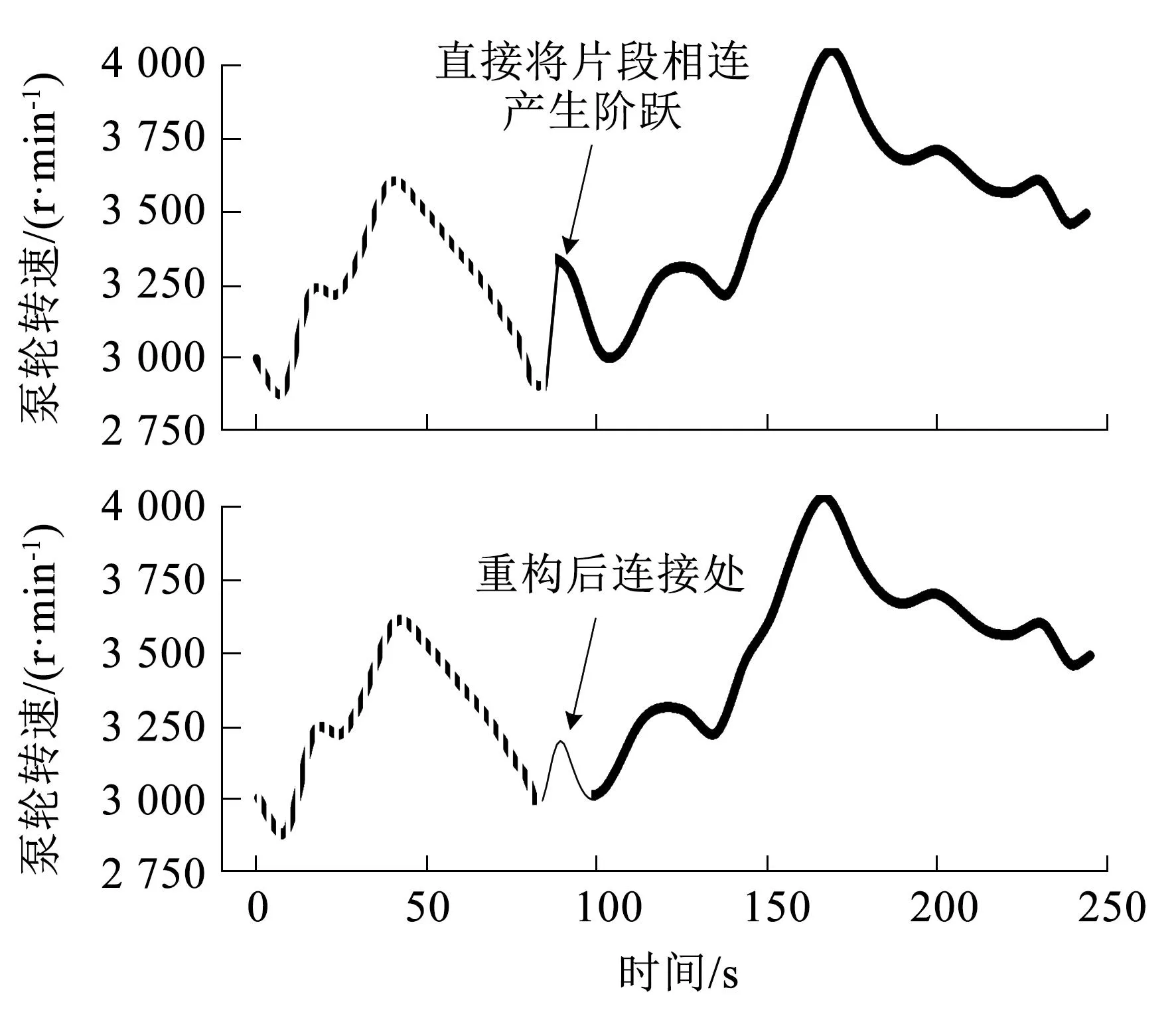
图7 加窗重构平滑连接效果Fig.7 Effect of smooth connection with window reconstruction
4.2 循环工况优化
设定目标循环工况时长为900 s,以循环工况与实车数据统计结果偏差最低、连接更平滑为目标,利用模拟退火算法对片段的选取进行优化,随后利用惯性权重线性递减的多目标粒子群算法(multiple objective particle swarm optimization-W,MOPSO-W)对片段的排列方式进行优化,使构建的循环工况尽可能真实反应实车运行特征。
4.2.1 片段选取方式优化
4.2.1.1 约束条件
结合变矩器的实际工作情况及数据统计结果,共建立了3项约束条件:
1)构建的循环工况中变矩器牵引工况占比目标为46.82%、反传工况占比目标为8.55%、闭锁工况占比目标为44.62%,阈值为0.1%。
(12)
式中:ni=1,CB=1、n0
2)循环工况中4类非闭锁工况片段占比应符合实车数据聚类结果如图4所示,对应阈值为0.1%。
(13)
式中:nx∈cj为第j聚类中的数据长度,pj为第j聚类占比,N为循环工况总长度。
3)循环工况中闭锁工况时长主要分布在200 s内,统计其片段时长占比见表4,阈值为0.1%。

表4 不同时长闭锁片段分布Tab.4 Distribution of atresia segments with different durations
(14)
式中:n10·j≤l<10·(j+1)为闭锁时长在[10·j,10·(j+1))秒内的数据长度,pj为总体数据统计中该区间内占比,N为循环工况总长度。
4.2.1.2 目标函数
选取平均速比、平均泵轮转速、平均涡轮转速、及4个速比比例系数共7个最主要表征参数作为优化目标,以片段集合与实车数据特征参数统计结果的相对误差值作为目标函数:
(15)
式中:γi(X′)、γi(X0)分别为循环工况与原始数据的特征参数,确保7个关键参数的相对误差值在5%以内,且以每个参数最大误差为目标作最小化寻优,以尽量降低构建循环工况与原始数据的偏差。
4.2.1.3 优化结果
利用模拟退火算法对片段选取方式进行优化,迭代130 196种组合后达到终止温度,优化后的片段集合特征参数优化前、后相对误差见表5。

表5 优化前、后的特征参数相对误差Tab.5 Relative error of characteristic parameters before and after optimization of selection method
如表5可见,通过对片段选取方式进行优化,有效控制了选取片段集的主要特征参数与实车数据的误差,优化后特征参数与原始数据的误差在2.4%以内。
4.2.2 片段排列方式优化
对选取片段的排列进行优化,以达到特征值平均误差最小、边界平滑的目的。
4.2.2.1 目标函数
为实现构建的循环工况对实车数据还原度高、连接平滑,提出以下3个量化指标作为目标函数进行优化:
1)循环工况同原始总体数据的特征值误差最小;
2)各连接处转速差值总和最小;
3)各连接处斜率差值总和最小。
(16)

4.2.2.2 寻优过程
计算寻优中所采用的优化算法为惯性权重非线性递减的多目标粒子群算法(MOPSO-W)[17],进行迭代优化计算,累计寻找样本点20 000个,最终优化的帕累托解53个,样本点分布如图8所示。
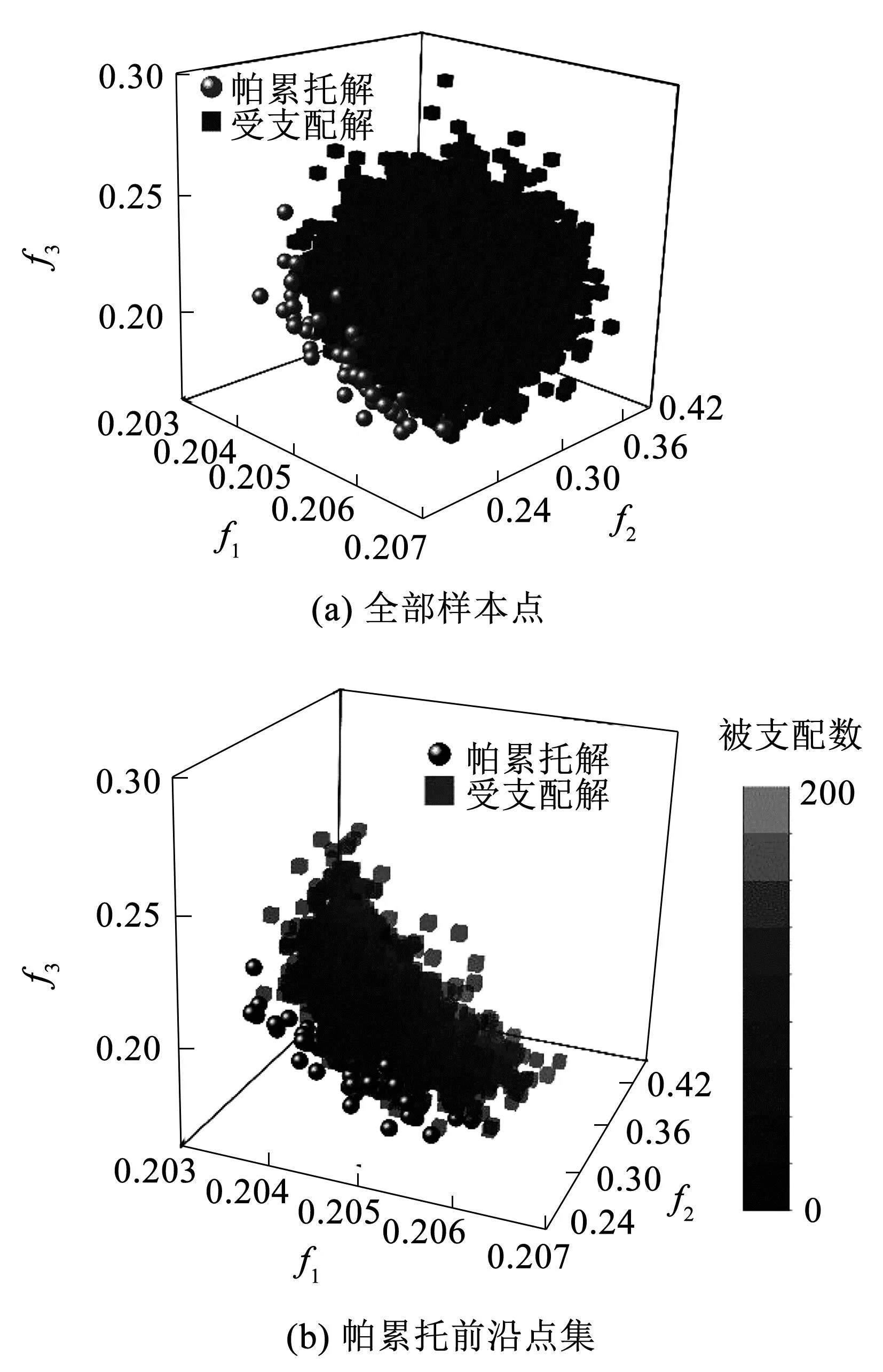
图8 优化结果分析Fig.8 Analysis of optimization results
4.2.2.3 优化结果
经过优化筛选,3个目标函数值分别为6.53%、387 r/min、31.05 r/(min·s-1),取最值归一化后坐标点为(0.202 9,0.334 9,0.185 5),最终构建液力变矩器循环工况如图9所示。

图9 液力变矩器循环工况Fig.9 Hydraulic torque converter cycle conditions and blocking oil pressure control signal
最终构建的循环工况主要特征参数与原始数据的关键参数见表6,相对误差均控制在4.20%以内,平均相对误差值为2.92%,表明构建的循环工况能够较好反映该型车用液力变矩器在实车运行中的工况特征。

表6 关键特征参数对比Tab.6 Comparison of all characteristic parameters
5 结 论
1)本文在履带式越野车辆实车数据的基础上,对液力变矩器工况特征进行了统计分析、降维和聚类,获得了液力变矩器在实际运行过程中的工况特征,从泵轮转速、涡轮转速两个维度出发构建了液力变矩器循环工况,建立优化模型对典型工况片段的选取及排列组合进行了优化。
2)统计分析过程中主要采用的方法为核密度拟合,明确了履带式越野车辆越野行驶需求,基于统计结果提出了平均速比、平均泵轮转速、平均涡轮转速等特征参数进行液力变矩器工况特征的统计。
3)利用主成分分析法将特征参数由22维降低到8维,用K均值聚类法对非闭锁工况片段进行聚类分析,得到起动加速工况、高效区工况、液力工况和反传工况等为主导的典型工况簇。
4)构建了循环工况片段选择及排列顺序优化模型,模型中使用了模拟退火和多目标粒子群优化方法,经过优化重构,循环工况的主要特征参数与实车数据误差控制在4.20%以内,平均相对误差为2.92%,能够较真实反映实车运行工况特征。
——变矩器的锁止控制

