星表核反应堆能量转换系统方案的初步优选与性能分析

张昊春，孙琦琦，孙梓健，张 诚

(哈尔滨工业大学能源科学与工程学院，黑龙江哈尔滨 150001)

随着航天技术的飞速发展，人类探索宇宙的脚步越来越快，截止到2021 年6 月，我国已经顺利完成了月球“绕，落，回”三步走的任务，也已实现了“祝融号”火星探测车的顺利着陆。为了更深层次地探测、开发和利用月球和火星资源，建设星表基地已经成为各个航天大国的重点航天项目。解决能源供给问题是星球基地建设的基础。因此大功率、高性能的核反应堆发电系统受到了众多研究者的青睐。美国和俄罗斯针对月球和火星基地提出了诸多空间核电站方案，根据文献统计，在32 个星表核电站方案中，美国占据27个，俄罗斯4 个，日本1 个[1]，其中SNAP-8[2]、SP-100[3]、Kilopower[4]、FSP[5]等均为美国典型星表基地核电站方案。

星表核反应堆电站包含核反应堆本体、辐射屏蔽、热电转换系统、热排放系统和控制系统5 个部分，其中热电转换系统是将核裂变释放的热能转换成电能的重要模块，循环热效率及输出功率等热力性能会直接影响整个系统的效率。星表基地热电转换方案的选取涉及众多因素，需要综合考虑系统质量-尺寸特性、安全性、可操作性、经济性以及与堆芯冷却方式匹配程度等，但目前提出的方案中热电转换模块主要以各国研究空间核动力的基础为基准，缺乏客观性。因此有必要将此多因素的定性问题定量化，从而客观地确定更适合于星表基地的热电转换方案。

本文通过对比分析现有方案，综合考虑星球基地对星表核反应堆电站的基本要求，构建热电转换方式评价指标和评价体系，利用层次分析法(AHP)对各项指标和备选方案进行权重计算，给出定量的决策结果，针对优选出的热电转换方案建立热力学分析模型，构建循环热效率表达式，并探究基本循环参量对系统性能的影响，从而为星表核反应堆电站设计的相关技术路线提供参考。

1 层次分析法

层析分析法是对复杂问题所包含的因素进行分析，将多种因素归并成不同层次，建立递阶层次结构分析模型，通过评价尺度构造判断矩阵，以量化形式反映定性问题，最后根据各因素权重确定方案[6]。图1 给出了层次分析法模型结构。

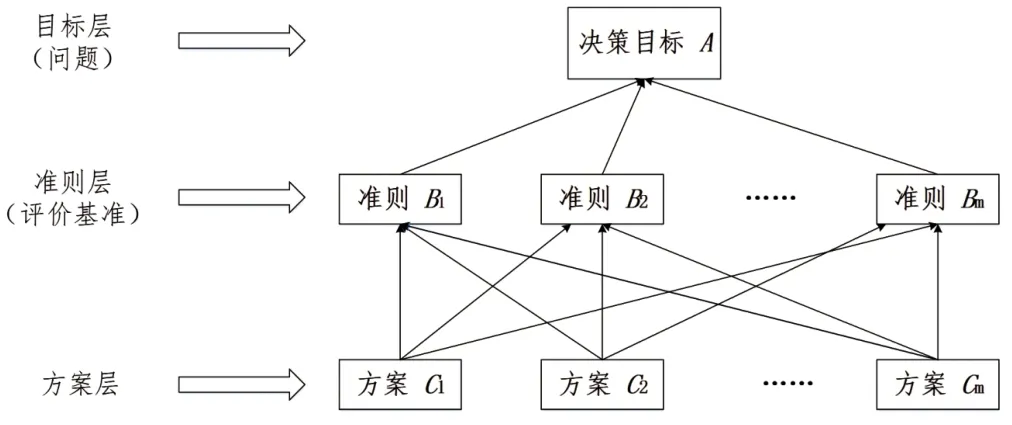
图1 层次分析结构模型

1.1 判断矩阵

基于上述层次分析结构模型，分别对准则层和方案层中的各个因子进行成对比较，依据评价尺度依次判断在同一准则下与之相关的各个因子之间的重要性，确定各层次中各因子的起始权重，从而构建各层次的判断矩阵：

式中：bij表示相对于要素A，因子bi与bj的相对重要性。

对各层次判断矩阵进行一致性检验从而确保由抉择者构造出的判断矩阵可以真实反映比较对象之间的关系，具有一定的可信度。判断矩阵一致性指标C.I.：

式中：λ为判断矩阵的最大特征值。

为了确保不同阶数的判断矩阵均满足一致性检验，引入一致性比例C.R.：

式中：R.I.为随机一致性指标，其值与矩阵阶数有关，见表1[7]。当C.R.＜0.1 时，认为判断矩阵是满意一致性矩阵。

表1 随机一致性指标(R.I.)

1.2 重要度计算

由于判断矩阵为正互反矩阵，因此可利用特征根法，如式(4)，对判断矩阵的特征向量进行标准化处理，确定各要素的权重值。由权重值进行层次单排序和层次总排序从而确定本层次中各因子与上层次中与其相关的各因子之间重要性次序的权重值以及同一层次中各因子的权重值，以此完成对备选方案的排序。

式中：w为特征向量，也即权向量，w=(w1,w2,…,wm)T。

2 热电转换方案分析

依据空间探测需求，运载火箭能力以及星球地理环境对星表核反应堆电站提出了几项要求[8]：足够的电功率和使用寿命、良好的环境适应性和可靠性以及高安全性和可承受经济性。即星表核电站应提供足够长久的电力，满足星表基地科研工作人员的基本生活需求和科学研究需要；其次为了防止星表环境变化、空间撞击等导致的系统失效，星表核电站需要具有一定的可靠性确保其在各种情况下持续稳定输出电力；另外，星表核电站应确保安全性，防止因系统失效导致有害工质泄露，从而对基地科研人员以及星表环境造成损伤；除此以外，还应充分考虑质量-尺寸特性，由于核电系统装置需由运载火箭送入指定星球，其结构、尺寸等因素不仅对运送难度有一定的影响，也会导致单位功率造价变化从而改变整个系统的经济性能。

2.1 方案评价模型

综上分析，选取质量-尺寸特性、可操作性、安全性、可靠性和经济性五个因素作为热电转换方式的一级指标，其次，以自身质量和散热器总面积为质量-尺寸特性的二级指标；以峰值压力，技术成熟度和使用寿命为安全性的二级指标。

利用层次分析法建立带有子准则层的热电转换方案评价体系，模型如图2。

图2 热电转换方式层次模型结构

2.2 方案选型分析

以月球基地核反应堆电站为例，若要满足月球表面科研、生产工作，需要100 kW 以上的电功率，热电转换方案中根据有无转动部件分为静态转换和动态转化，其中动态转化是利用高温高压的气态工质推动透平后带动交流发电机，从而实现了热能向机械能再向电能转换的过程。动态转换的热效率相对较高，依据热力循环方式主要包含朗肯循环、布雷顿循环和斯特林循环。以电功率为100 kW 的SP-100系统为例，对SP-100 反应堆耦合三种动态转换系统进行分析[9]，依据各项评价指标进行方案打分，并根据层次分析模型结构确定各指标权重。

表2 和表3 展示了各指标权重：安全性对星表核电站的权重最大，占比41.82%，对方案选型起决定性作用，其次依次为质量-尺寸特性、可靠性、可操作性和开发成本；二级指标中系统自身质量权重大于散热器面积，使用寿命权重大于峰值压力和技术成熟度。这表明：星表核反应堆电站热电转换方案设计中最重要的是确保安全性，并在此基础上持续稳定地供电，因为星表基地电站不同于空间核电站，其主要为宇航科研人员科学探索和居住生活提供电能，确保其安全稳定地运行对科研工作者具有重要的意义。根据各评价指标权重，对三种动态转换方案进行分析可知，布雷顿循环转换权重为36.23%，高于朗肯循环和斯特林循环，且层次总排序一致性比率为0.092 4，满足一致性条件，因此可以将布雷顿循环作为星表核反应堆电站热电转换基础方案。

表2 层次单排序及其一致性检验结果

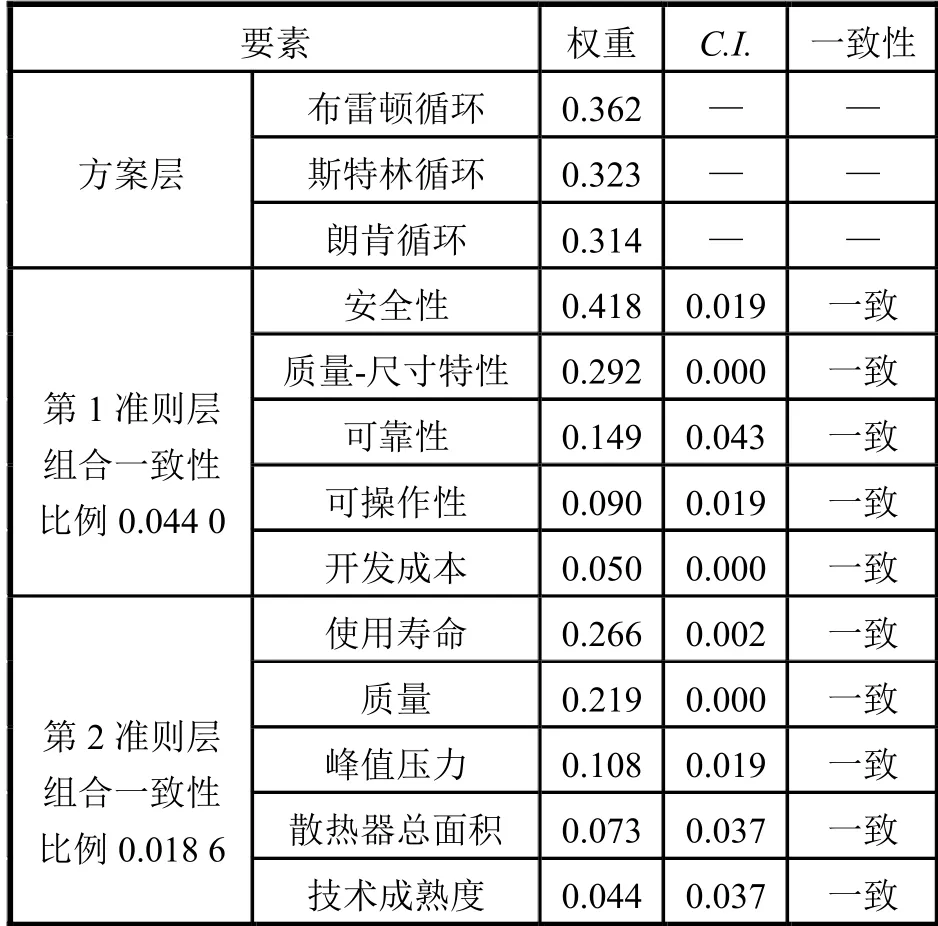
表3 组合一致性结果

3 热电转换模块结构讨论

3.1 系统结构物理模型

根据层次分析法分析结果选用布雷顿循环作为星表基地核电站的热电转换方式，其包含等压吸热(堆芯)、绝热膨胀(透平机)、等压放热(冷却器)和绝热压缩(压缩机)四个理想过程。图3 给出了布雷顿循环系统装置和热力学模型。

图3 布雷顿循环系统

为了进一步提高热电转化效率从而提高整体系统效率，以传统闭式布雷顿循环为参照模型，在此基础上进行相应的改进，形成不同结构的布雷顿循环系统。考虑到星表基地核电站的特殊性，需在提高系统效率的同时，减小系统质量，增加系统安全性和可操作性等，因此，热电转换系统结构不易过于复杂。针对参考文献[10-11]提出的多种布雷顿系统结构，本文重点对回热式、预压缩式、再压缩式和简单中间冷却式4 种结构(图4)进行热力学分析以此确定更适合于星表基地的热电转换结构。

图4 布雷顿循环结构

3.2 系统结构数学模型

文献[12]对回热式模型的系统效率做了详细的推导，下文以较为复杂的再压缩布雷顿循环为例，建立单位质量流量的热力学模型。假定循环系统为理想状态且不考虑工质在管道中的热损失，即部件进口温度等于上一部件出口温度，循环工质为氦气，循环系统各状态点如图4(c)。

首先定义两个参数：系统压缩比πC和回热度f。压缩比为工质在压缩过程的终点压力与起点压力之比；回热度为工质在回热器中实际吸收热量与工质在回热器中理论放出热量的比值。

循环系统吸热量Qin：

式中：Cp为循环工质定压比热容；Ti为各状态点温度。

系统净功Wnet等于系统膨胀功与压缩功的差值，也等于工质在堆芯吸收的热量与工质在冷凝器放出热量的差值，即：

式中：x为分流比。

忽略回热器自身的散热损失，高/低温回热器满足能量守恒，即：

回热度定义得高/低回热器回热度f1，f2[13]：

式中：ΔTmax为低温回热器最大冷热温差。

回热器为定压放热/预热过程，可得透平机出口温度T6：

式中：k为比热容比。

综上可得：循环净功Wnet、系统吸热量Qin的最终表达式为：

式中：πMC为主压缩机压缩比；πRC为再压缩机压缩比。

系统效率定义为工质完成循环的净功与加入系统的热量之比，即：

其余模型可采用相同的热力学分析方法建立数学模型，此处不再赘述，具体结果如表4。

依据表4 可知：不同构型布雷顿循环系统的基本循环参量为反应堆出口温度TR，冷却器出口温度TC，压缩比πC和回热度f的函数。因此，探究基本循环参量对不同构型系统循环热效率的影响，并结合星表基地对核电系统的要求确定具体的热电转换方案。

3.3 系统性能计算与分析

以Li 热管冷却反应堆耦合闭式布雷顿循环作为星表基地核电站方案，余热排放装置以热管式辐射散热器为主。首先选取工况参数：运用布雷顿循环的空间反应堆出口温度TR取1 000～1 600 K[14]；压缩比πC取1.5～5[15]；回热度f取0.5～0.95[15]；冷却器出口温度TC对余热排放系统影响较大，降低冷却器出口温度可有效提高热电转换效率，但同时也会增大辐射散热器面积从而降低核电系统质量-尺寸性能，综合考虑TC初步取300～800 K[16-17]；因本文着重探究以上四个工况参数对系统性能的影响，故简化参量确定分流比x取0.7[18]，压缩机压缩比为1，且主压缩机、副压缩机及预压缩机的压缩比保持相同。以下详细探究工况参数在一定变化范围内，不同结构布雷顿循环系统性能变化。

图5 中，Model1 为基础模型，Model2 为回热式，Model3 为再压缩，Model4 为预压缩，Model5 为简单中间冷却。图5 给出了不同模型循环比输出功率随工况参数的变化规律。随πC的逐渐增大，Model1 循环比输出功率始终增大，其余模型呈现先增大后减小的趋势；随TC增加，除Model1 维持持续增长的趋势，其余模型循环比输出功率均逐渐降低；随TR逐渐增加，Model1 循环比输出功率不变，Model2，3，4，5 循环比输出功率均持续增大；f对系统循环比输出功率无影响。综合分析，Model5 的循环比输出功率在不同循环参量变化过程中均保持最大值，具有明显优势。

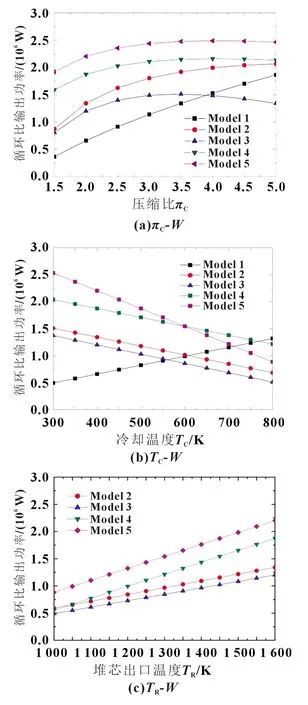
图5 热电转换循环比输出功率变化

图6 给出了不同结构热电转换效率随工况参数的变化规律。各个模型的效率随参数改变的变化趋势相同。πC对系统效率的影响与πC对循环比输出功率相同，其中Model2 和Model3 对πC变化较为敏感，当TR为1 600 K，TC为400 K，f为0.85 时，分别在πC为3 和2.5 时取得效率最大值；Model1 的效率是πC的单值函数，因此当TR，TC和f改变时，其效率仍然恒定不变，为一条直线，如图6 (b)、(c)、(d)，其余模型随着TR升高，TC降低，效率逐渐增大。其中，Model4 对TR最为敏感，TR由1 000 K 上升至1 600 K，效率增长率达78.73%；Model5 对TC的变化最为敏感，当TC小于600 K 时，Model5 效率迅速增加，远高于其他模型；f虽然对循环比输出功无影响，但增加回热器可回收余热再利用，有助于提高循环效率，因此随f增大，各个模型效率均有提升，Model2 效率增加最为明显。与图5 研究结果相同，Model5 的热力性能也是最优的，其循环热效率最大。

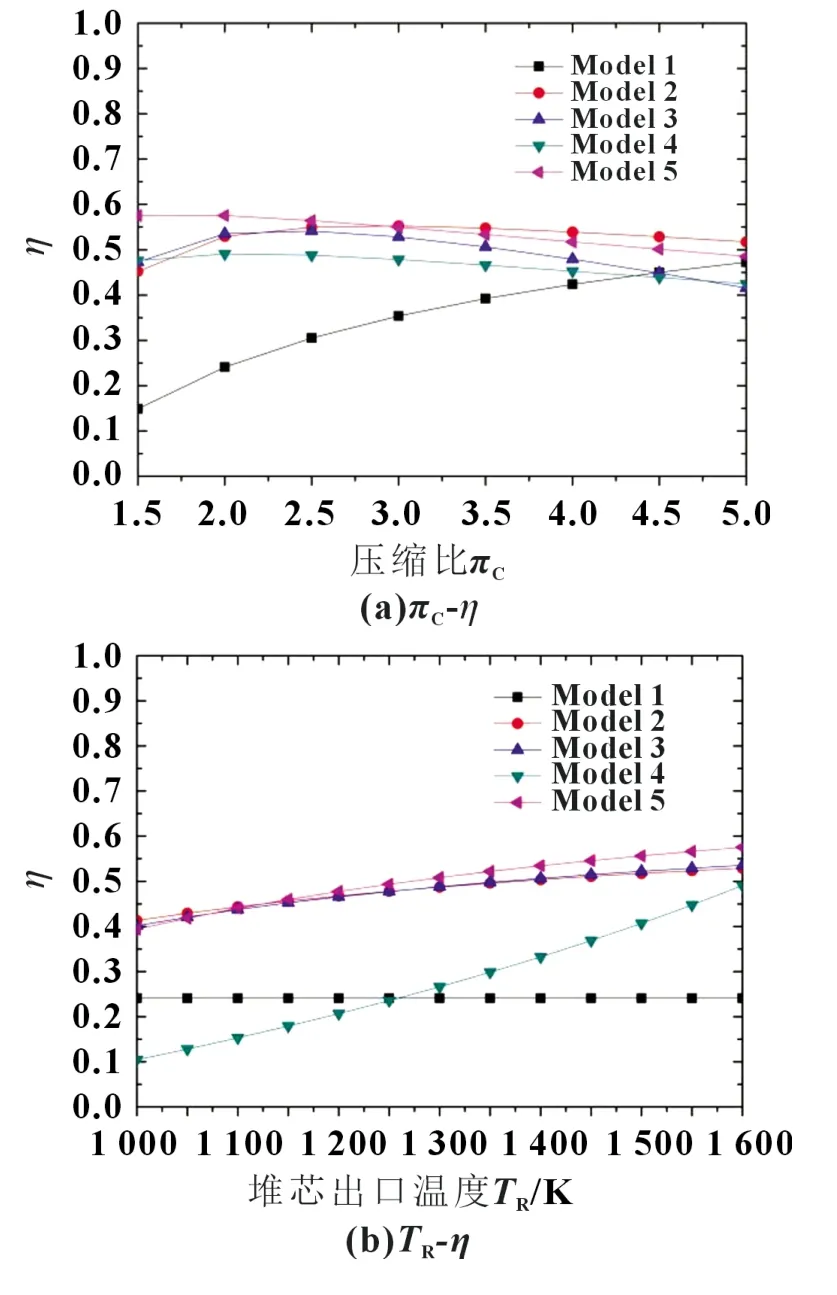
图6 热电转换效率变化

为了进一步对比分析布雷顿循环系统结构变化对循环参量的敏感性，首先以Model1 为基准，堆芯出口温度1 600 K，冷却温度400 K，回热度0.85，各个模型与基准模型效率比值为研究参量，分析效率比值随πC变化的趋势；再以πC=2 的Model1 为基准，探究TR、TC和f对效率比值的影响，结果如图7。

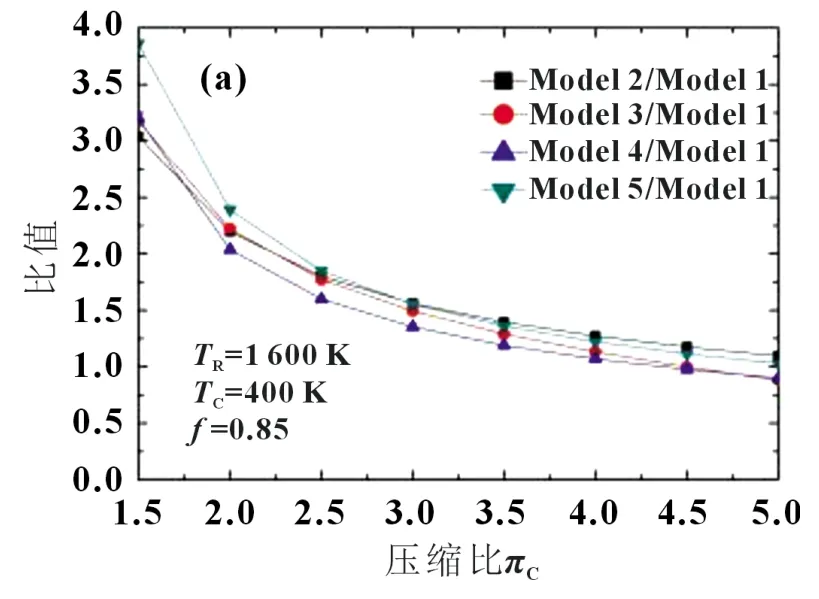
图7 热电转换系统循环热效率比值变化

图7 给出了热电转换系统循环热效率比值的变化规律。在πC变化过程中，各个模型的起始效率均大于基础模型，但随着πC增大，基本模型的效率增长率逐渐大于其余模型的变化率，因此，效率比值持续下降，尤其是Model3，当πC为5 时，其效率比值减小了12.09%。

以πC=2 的Model1 为基准，循环热效率比值的变化规律显示：TR变化过程中，温度在1 000～1 250 K 范围内，Model4 效率始终小于Model1，在1 250～1 600 K 范围内，Model4 效率逐渐增大，当TR为1 600 K 时，效率比值为2.04；随TC，f变化，不同模型的效率比值变化梯度相似，整体范围均处于1.0～3.0 的波动带中。

综合对比分析，在不同循环参量变化过程中，Model2、Model3 和Model4 对不同工况参数变化更为敏感，效率曲线变化梯度较大；Model5 虽然相比于其他模型，受冷却器出口温度影响明显，但当冷却器出口温度低于600 K 时，系统循环比输出功率和热电转换效率始终为5 种模型中的最高值，且Model5 对其他工况参数变化的敏感性较低，有助于保持系统稳定性。另外，Model5 简化了再压缩系统的分流部分，预压缩系统的回热部分，结合星表基地核电站评价体系给出的结果可知：在确保同等供电性能的基础上，Model5 更容易操作和控制，具有更好的质量-尺寸特性。因此，可将Model5(简单中间冷却循环)作为星表核反应堆电站热电转换最终方案。

4 结论

本文对星表核反应堆电站的热电转换方案进行探究，得到以下几个结论：

(1)利用层次分析法对星表核反应堆电站的动态热电转换方案构建多维度评价指标，确定安全性对星表核电站的权重最大，占比41.82%，其次依次为质量-尺寸特性、可靠性、可操作性和开发成本；综合分析优选布雷顿循环系统作为初步方案。

(2)对回热式、再压缩式、预压缩式和简单中间冷却式4 种布雷顿循环结构构建热力学分析模型，给出不同模型的效率表达式，并以此确定影响热效率基本循环参量：压缩比πC、反应堆出口温度TR、冷却器出口温度TC和回热度f，即η=F(πC,TR,TC,f)。

(3)探究工况参数变化对不同结构循环系统效率的影响可得：随πC的增大，各模型效率呈现先增大后减小的趋势；随TR升高、f增大、TC降低，各模型效率呈现持续增大趋势。

(4)简单中间冷却结构对循环参量的敏感性最低，且在不同工况下均具有明显的循环热效率和比输出功优势。因此，可将简单中间冷却系统作为星表基地核反应堆电站热电转换方案。