一种用动态神经网络的月面科研站电源系统分析方法

黄宇超，宋相毅，童乔凌，张 侨

(1.武汉理工大学自动化学院，湖北武汉 430070；2.华中科技大学集成电路学院，湖北武汉 430074)

月面科研站的正常运转离不开能源系统，能源主要以电能供应为主。电能的来源大部分来自于光伏发电，当没有太阳光时，主要由蓄电池供电。月面科研站主要任务包括地质勘探、环境监测、科学实验等，另一方面，月球表面辐射和温度变化大，这些导致设备工作环境复杂，干扰大，对电力电子变换器的控制提出更高的要求。电源级联系统用常态分析方法进行建模十分复杂，分析起来十分困难。若通过深度学习的方法，将电源级联系统等同于黑箱模型，采集其端口特性，利用神经网络对电源级联系统进行分析[1]。

电源级联系统都具有非线性特性，因此使用神经网络进行系统辨识成为了一种可行的解决方案。静态神经网络，如前馈神经网络(FNN)已经能够逼近非线性系统的基本特性，是建模非线性系统的有利工具。动态神经网络(DNN)也称为递归神经网络，常用于非线性系统辨识。连续时间Hopfield-type 动态神经网络类克服了上述提到的缺点。目前研究表明有多种表征DNN 非线性建模的方法，其控制方式的应用也被提出。深度神经网络可以近似形式为(t)=f(x(t))的n维系统，通过对参数的优化和更新网络结构中的权值和偏置值，获得接近期望的结果[2]。

本文首先介绍了神经网络和其动态建模的一些重要背景，讨论了如何正确建立模型和训练网络以模拟任何给定电力电子转换器。选取Buck 电路作为研究对象，采用MATLAB 的Simulink 模块得出神经网络的训练数据集，通过仿真结果与神经网络训练结果进行对比，验证了该方法的合理性，最后对文章内容进行总结，并简要对未来的研究方向进行展望。

1 神经网络架构

1.1 神经网络背景介绍

神经元的一般结构如图1 所示，每个神经元都是一个多输入单输出的系统。通过将输入进行线性组合，加入偏置函数进行修正，最后经过一类典型的非线性“激活函数”得到输出结果。激活函数有多种，常用的激活函数是双曲正切函数：

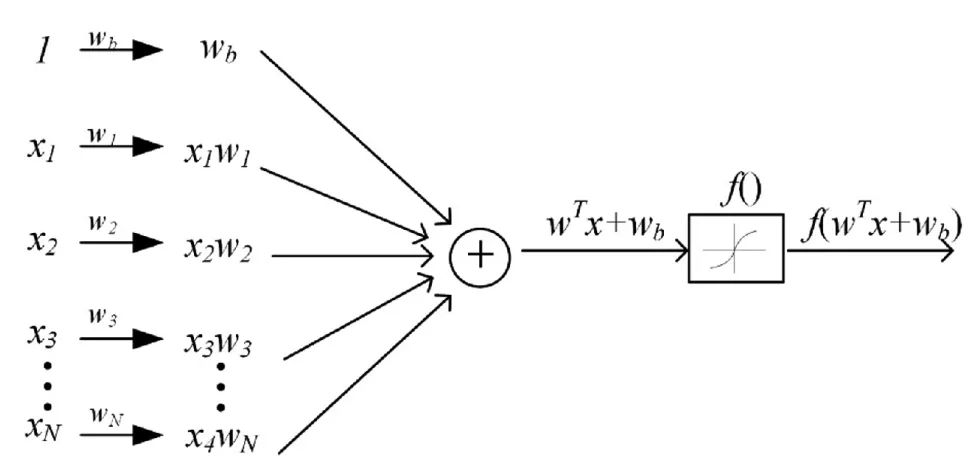
图1 神经元的一般结构

神经元的互联可以采取多种形式，每种形式都会产生不同的神经网络结构，能力、优势和缺陷也不一样。总体上看，神经网络都是分层结构的，若信号在网络中每一层的每个神经元都接受前一层所有神经元的输入，并将其输出传递给下一层的所有神经元，这种连接形式称为全连接，如图2 所示。

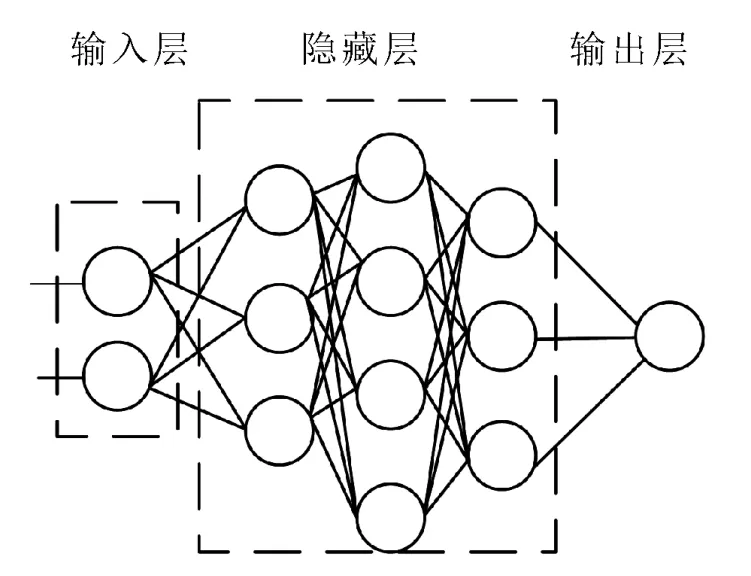
图2 神经网络全连接示意图

1.2 长短记忆神经网络分析

在神经网络模型中，前馈神经网络(FNN)使用范围很广，但作为静态神经网络，其输入信息单向的从输入层经过隐藏层到达输出层，至少需要3 层才能实现函数逼近，隐藏层数越多，每一层包含的神经元数量越多，结果将会越精确。但对于一组固定的输入，输出也不会变化，这不利于建模由微分方程系统描述的动态系统，即FNN 不具有记忆性[3-5]。

在文献[3]和文献[4]中提出了使用神经网络进行电力电子转换器建模，作者均选用了FNN，其中文献[3]提出使用FNN 预测单相全桥二极管整流器的输出电压，由于负载包含电感电容，对输出电压的预测不能很精确；文献[4]中加入了仿真时间向量作为输入，但仅在模拟环境下具有意义，不能通过阶跃响应测试。

长短记忆神经网络(LSTM)是时间序列分析中应用广泛使用的模型,它主要是为了解决长序列训练过程中梯度消失和梯度爆炸的问题。LSTM 通过门单元和记忆单元来处理在一段时间内数据的收集[4]。LSTM 旨在维护具有长期依赖性的问题，在所有循环神经网络(RNN)中，包括一个单独的tanh 层，其具体重复单元模块如图3 所示。与标准RNN 类似，LSTM包含如图4 所示的链结构，在RNN 结构的基础上进行了进一步的改进。

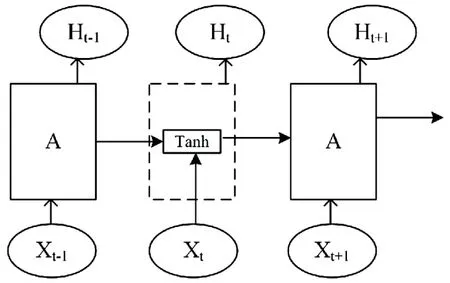
图3 RNN中重复模块

图4 LSTM中重复模块

LSTM 可以包含或排除来自单元状态的数据，这些数据由“门”的结构精心管理。门是一种控制数据是否可以进入单元状态的方法，是sigmoid 函数和逐点乘法过程的组合。对于LSTM，使用不同的门将数据从一个单元传递到另一个单元，这些门被称为更新门、遗忘门和输出门，如式(2)～(4)所示。输入值和输出值都需要使用，数据通过水平线传递，水平线为图4 的最高点，这条水平线被称为单元状态，直接沿着整个链条向下运行[6]。

2 LSTM 搭建流程

本文选择了LSTM 作为非线性动态建模的框架，现在讨论如何实际使用网络来创建一个好的模型。一般而言，神经训练算法会自动为网络选择权重，即“拟合”模型的工作都将自动完成。但在训练模型之前，还需要考虑以下3 个步骤，即选择合适的输入和输出、创建出合适的训练数据并选择合适的超参数。

2.1 选择模型的输入和输出

基于LSTM 神经网络也需要选取合适的输入和输出，才能具有实际意义。对于功率变换器，LSTM输入应该是控制单元对变换器功率器件进行控制所需的参数，例如开关管占空比、变换器的输入电压、电感电流或负载电压和电流。LSTM 的输出应该是变换器中衡量系统能否稳定的指标，例如电感电流、负载电压。

2.2 创建训练数据

本文采用MATLAB 中的Simulink 模拟Buck 电路而不是真实的硬件测量来生成训练数据。采用仿真数据虽然不能代替实际的硬件电路，但也有很多优点，包括便利性、灵活性、对训练数据的完全控制、零测量噪声。由于经过训练的LSTM 的目标是在广泛的条件下紧密地复制转换器的动态行为，因此训练数据集必须包括尽可能多的工作状况。在电力电子变换器中，经常使用传递函数来描述变换器的开关平均动态行为，在特定的工作条件下，这些传递函数代表了变换器的频率响应。因此，当训练LSTM网络来对变换器建模时，训练集必须在变换器输入时考虑带宽，这样才能从训练集中学习到变换器的频率响应。

2.3 选取超参数

在机器学习中，超参数不是指通过训练得出的参数，而是控制模型结构或训练过程的参数。在LSTM 中，超参数包括但不限于：

(1)控制模型结构：如神经网络层数，每层的神经元数量和每层神经元的激活函数，LSTM 门函数的选取。网络层数和神经元数量过少会导致模型学习效率低，但过多并不会显著提高学习效率，反而会增加计算时长，浪费计算资源。一般而言，网络层数至少要3 层，每层的神经元数量至少包含10 个。激活函数选取很多，例如sigmoid、tanh(正切双曲线)、ReLU(整流线性单元)等。门函数取值范围一般在[0,1]之间。

(2)梯度下降训练算法或者任何训练算法下特定的参数，比如梯度下降训练算法中的α(学习率或步长)，步长太小会导致运算时间过长，步长太大容易错过最优解，α取值范围是[0,1]。

(3)性能指标，如均方差、平方差等。例如，将实际输出与预测输出进行均方差运算，得出的值理论上越小说明学习效果越好，通过人为设置可接受的最小误差，能够提高训练速度，误差可取1×10－6作为参考。

所有这些超参数的选择导致了大量可能的网络配置，这可能会使纯粹的试错训练成为一项困难而乏味的任务。然而，通常最重要的超参数是那些与网络结构相关的超参数，即网络层数、神经元个数、激活函数和门函数。训练算法、误差度量可以在必要时进行调整，但如果保留它们的经验值，一般是没有问题的。

3 电路拓扑选择及验证

3.1 电路拓扑分析

电源系统中电力变换离不开DC-DC 变换，将多种拓扑进行级联才能完成需要的电力变换功能，其中最为典型的电路便是升压电路和降压电路。电源系统稳定性分析常规方案是进行小信号建模，通过开环零点判断系统能否稳定工作，而级联电路主要采用阻抗判据分析稳定性，这些方案需要确定电路具体拓扑。采用LSTM 进行分析，可以只关注电路部分数据，对电路状态进行判断。LSTM 通过训练，在出现扰动输入时，能提前预测出系统输出变化。对预测输出数据进行分析，若处于系统的额定工况范围内，说明系统在该扰动下能保持稳定运行，否则可以触发系统的保护功能。

Buck 电路作为降压电路典型拓扑，具有重要的研究意义。Buck 电路不能代表整个电源系统，但作为电源系统的一部分，可以通过选取Buck 电路进行训练，验证LSTM 能否准确预测输出，为稳定性分析提供保障。

3.2 Buck 模型验证

Buck 电路建模简单，可以直接进行状态空间方程建模仿真，但对于非稳态的工况输出预测并不理想。对于常规仿真来说，采用动态神经网络的方法能在不改变电路的情况下，在线对可能的输出进行预测从而避免干扰造成严重的影响。常规仿真大部分只能够离线进行仿真，在线仿真具有入侵性，会增加设备的负担，并且相比于动态神经网络的方法误差更大。

从经验上可以得知，一个好的模型拟合需要至少两个隐藏层，每一层至少10 个神经元。在超过这个规模后，在某些情况下会带来一些边际性能收益或产生过拟合现象。为了平衡准确的性能和相对较低的计算成本，选择三个隐藏层的网络，第一层隐藏层8 个神经元，第二和第三层隐藏层10 个神经元，每一层均使用了式(1)中给出的双曲正切激活函数。

在训练算法完成RNN 的权重调整后，使用不同的数据集来测试模型，以验证模型是否正确学习了系统的动态行为。训练后测试结果表明，所提出的方法可以产生一个高度精确的模型，既能密切跟踪稳态解，也能跟踪各种瞬态条件和噪声扰动。测试故意让模型受到极端瞬态和大幅噪声的影响，以在“最坏情况”的场景中锻炼模型，并推断能跟踪这些条件的模型可以跟踪任何正常场景。

图5 为LSTM 训练模型。

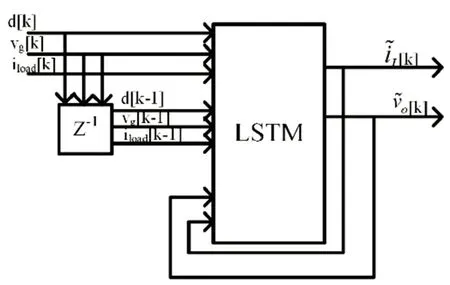
图5 LSTM训练模型

首先用MATLAB 中Simulink 模块搭建Buck 变换器，Buck 变换器能够在输入为48 V 的直流电压下稳定输出12 V 直流电压。但仅仅稳定情况下的输入数据对于LSTM 神经网络训练，虽然结果上预测输出拟合度很高，但不足以证明该方法的特殊性，故在Buck 本身能稳定的情况下，改变输入电压。本文输入电压集包含了不同频率的正弦信号，训练集如图6所示。其中，Vg为输入电压，il为电感电流，Vo为输出电压。由于频率设置过低负载输出仍为12 V 稳定电压，所以正弦信号频率需选设置1 kHz 以上，故得出的输出虽然不是稳定效果，但对于LSTM 网络训练是友好的。训练集从时间上分布是：第0～0.01 s 为48 V 直流输入；第0.01～ 0.04 s 为48 V 频率为1 000 Hz 的交流输入加上-4 V 的直流输入；第0.04～0.07 s为2 V 频率为5 000 Hz 的交流输入加上48 V 的直流输入；第0.07～0.1 s 为2 V 频率为1 000 Hz 的交流输入加上-48 V 的直流输入；第0.1～0.13 s 为24 V 频率为1 000 Hz 的交流输入加上24 V 的直流输入。将所测得输出作为LSTM 的输入和输出便可以对LSTM网络进行训练，如图7 所示。均方差为1.6×10-7，迭代次数为1 000 次。

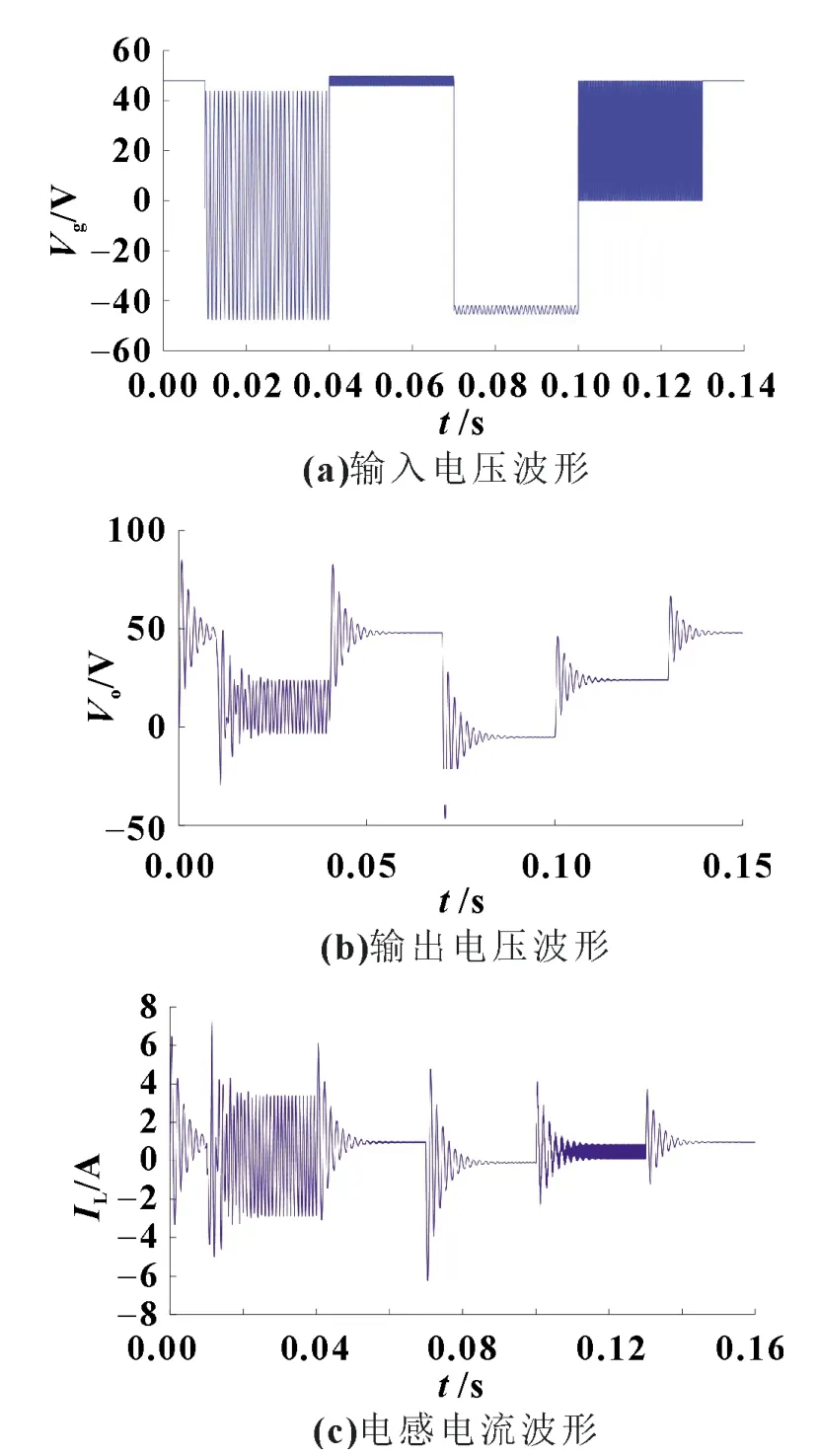
图6 输入训练集

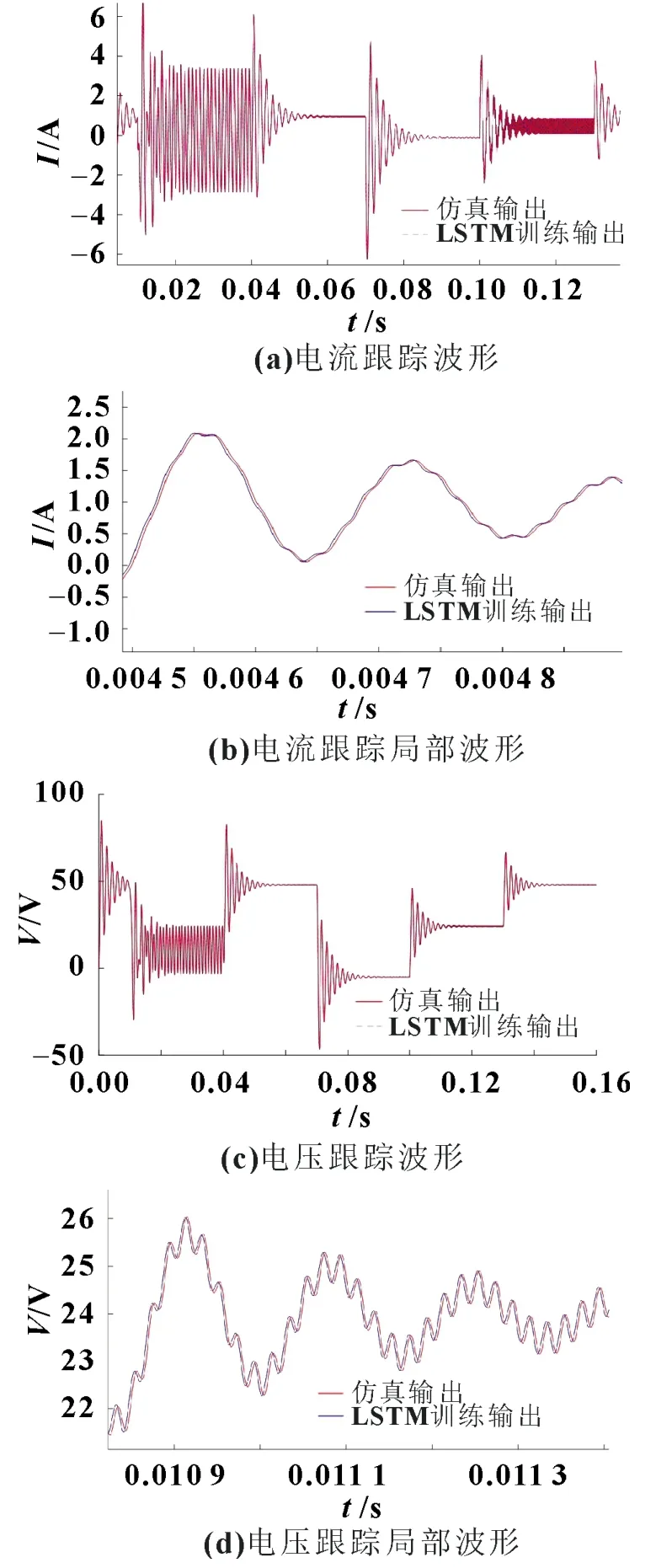
图7 电流电压跟踪波形

均方差较低说明跟踪效果良好，迭代次数较多，说明LSTM 模型有待优化。对于不合理的输入，实际电路是不能够产生如图6(b)中的输出，Simulink 能够对这些输入产生可能的输出。图7 中可以看出预测输出能很好跟踪仿真输出，无论其是否合理。当不符合工况的预测输出出现时，如图7 中[1 000,5 000]、[7 000,10 000]，可以判断系统不稳定。

本文还搭建了48 V 转12 V 的功率平台，如图8所示。为了更好地展示跟踪效果，将功率平台的ADC 采样数据经过数字滤波后通过CAN 导入到MATLAB 工作环境中，并对Buck 电路输出电压和电感电流的波形输入LSTM 网络进行训练，得出的训练结果能够很好地贴近电感电流和输出电压，均方差为3.6×10-7，迭代次数为905 次。均方差在允许的误差之内，预测结果能很好地跟踪实际波形，说明电路工作在稳定状态。图9 为Buck 电路稳态跟踪波形。

图8 Buck电路硬件平台

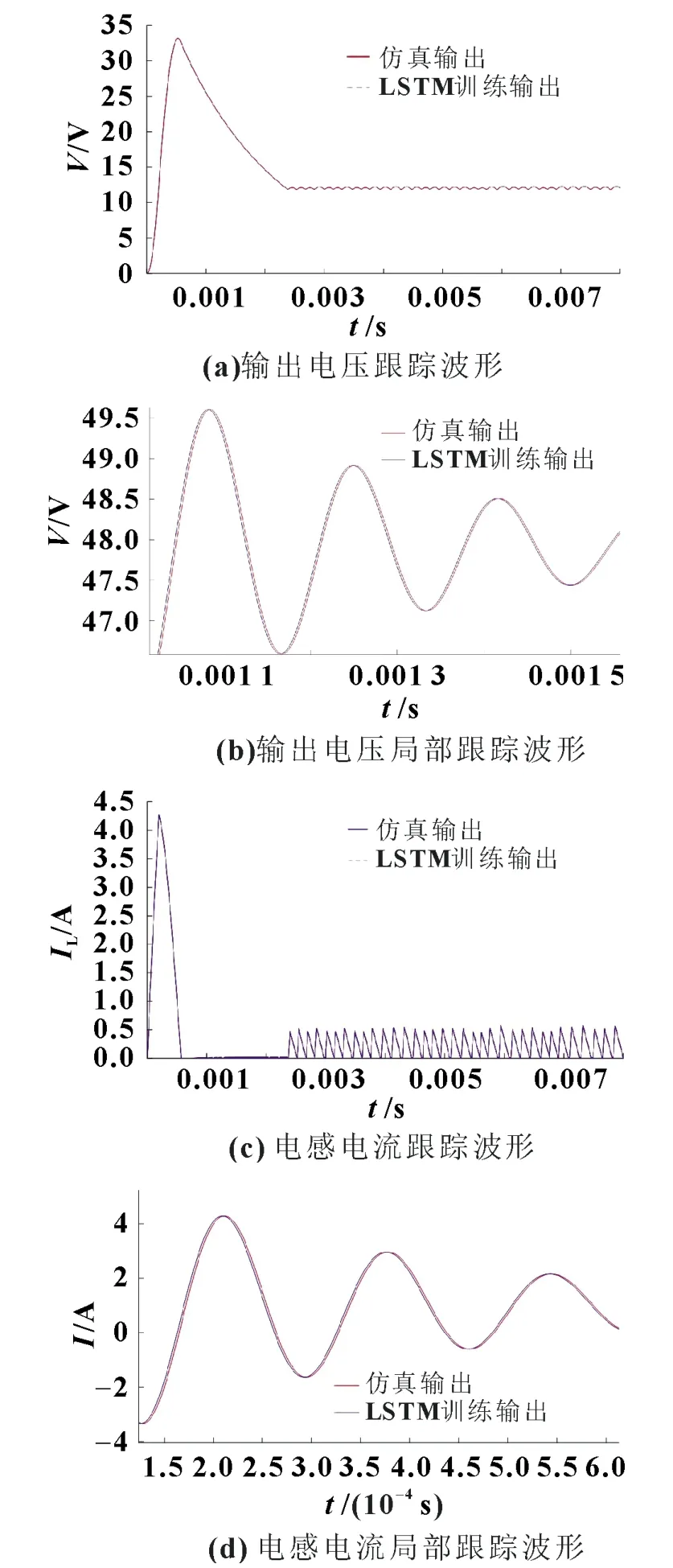
图9 Buck电路稳态跟踪波形

通过仿真和实物验证，LSTM 训练的输出能很好地跟踪实际输出。对预测输出进行分析，若预测结果不稳定，说明实际电路输出也不稳定，此时应该对电路进行保护处理。神经网络建模均存在一个最为明显的缺点，意外行为的可能性无法消除，尤其是当要求神经网络评估输入与训练集中包含输入相差太多的时候。在训练模型的时候尽可能地提供更多的输入，只有在训练数据足够大的情况下才能训练出更好的模型。对于仿真而言，输入噪声可以任意改变，但不可能展现所有可能存在的输入变化，仅以上4 种噪声进行展示，验证该方法的有效性。

4 总结与展望

本文提出了一种新的功率变换器建模技术，对建模后的数据进行分析，无论是仿真模型还是实物上预测输出都能很好地跟踪实际输出，因此可以通过预测输出判断系统能否达到稳态工况，即输出波动和范围是否达到稳定要求。该技术特别适合于创建开关平均、大信号、实时的变换器数字孪生模型。只要计算性能达标，模型可以在任何平台上运行，比如在变换器的嵌入式控制器上运行。另一方面，该模型在未来可能用于故障检测、预测和健康管理以及风险评估等功能。

该模型在未来还有很大的发展空间。首先，我们希望将训练好的模型嵌入工作环境中，并探索模型的计算速度。如果计算资源对于特定的嵌入式平台来说成为问题，我们可以探索模型压缩技术来减少计算资源。激活函数对计算资源也会产生显著影响，因此我们可以探索使用更简单的激活函数，能否可以达到与sigmoid 激活函数相似的精度。

此外，在闭环反馈控制系统中，LSTM 模型输出的结果是转换器瞬态行为，我们认为一个经过良好训练的模型应该足够接近实际转换器的动态行为，对于动态的控制系统能否使用LSTM 网络进行训练仍有待实验证明。最后，我们可以将这项工作扩展到现代电力系统应用中发现的其他动态组件，如发电机、电机和储能系统的建模，为电力系统创建一个完整的数字孪生目录。