基于深度学习 GRU 网络的 UWB 室内定位优化
郑宏舟 赵宇宸 孟飞

摘要:为减少信号传输质量和距离估计算法等因素对定位精度的影响,将深度学习应用于超宽带(ultra wide band,UWB)室内定位系统,利用门控循环单元(gated recurrent unit,GRU)网络代替 传统UWB室内定位系统中的三边测量过程,以提高UWB室内定位精度。在得到定位标签到基站的距离信息后,将距离信息输入GRU网络中,输出最终位置坐标。GRU作为循环神经网络(recurrent neural network,RNN)的变种,既含有RNN处理时序数据的优势,又解决了RNN中 的长程依赖问题。对GRU网络模型中不同学习率、优化器、批量大小、网络层数、隐藏神经元数量参数进行调整和训练。结果表明,基于GRU网络模型的UWB室内定位系统显著提高了定位精度,平均定位误差为6.8cm。
关键词:超宽带室内定位;神经网络;深度学习;门控循环单元
中图分类号:TP 183 文献标志码:A
Optimization of UWB indoor localization based on deep learning GRU networks
ZHENG Hongzhou, ZHAO Yuchen, MENG Fei
(Business School, University of Shanghai for Science and Technology, Shanghai 200093, China)
Abstract: In order to reduce the influence of signal transmission quality and distance estimation algorithm on the localization accuracy, deep learning was applied to the ultra wide band(UWB)indoor localization system, the gated recurrent unit(GRU)network was used to replace the traditional trilateral measurement, to improve the indoor localization accuracy of UWB. After get the distance from the localization tag to the base station, the distance information was input into the GRU network, and the final localization coordinates were output. As a variant of recurrent neural network(RNN), GRU not only had the advantages of RNN in processing time series data, but also solved the long-term depenencies problem in RNN. The parameters of different learning rate, optimizer, batch size, network layer and the number of hidden neurons in the GRU networks model were adjusted and trained. The result showed the UWB indoor localization system based on the GRU networks model improved the localization accuracy significantly, the average localization error was 6.8 cm.
Keywords: ultra wide band indoor localization; neural networks; deep learning; gated recurrent unit
當无法在室内环境中使用卫星定位时,可利用室内定位技术[1]作为卫星定位的辅助定位,解决卫星信号到达地面时信号微弱、无法穿透建筑物的问题。传统的超宽带(ultra wide band ,UWB)室内定位系统的定位精度主要受信号形状、信号到达时间(time of arrival ,TOA)以及基站与标签之间距离计算方法的影响,在得到各基站与标签的距离后,使用三边测量法计算标签位置。为使三边测量法的计算足够精确,要求标签与基站之间的距离估计误差必须足够小。时钟同步精度、多径传播、信号传播条件、多址干扰、信号形状等都会影响标签与基站之间距离估计的精度,这是传统 UWB 室内定位系统的主要误差来源。目前,主流室内定位技术的精度为20~90 cm,为提高传统 UWB 室内定位系统的精度,本文将深度学习与 UWB 室内定位系统相结合,利用门控循环单元(gated recurrent unit ,GRU)神经网络构建定位模型。
过去已有关于 UWB 测量应用于室内定位的研究,如基于 TOA[2]、惯性测量单元[3]、UWB 和行人航位推算融合[4]、自适应抗差卡尔曼滤波[5]。文献[6]从室内定位算法、测量技术和融合定位技术3个方面对各种室内定位技术进行梳理,并对距离测量、指纹定位、即时定位与地图构建技术、惯性导航等多种适用于不同场景定位技术的基本原理进行综述,从定位技术特点、定位需求的角度对各种定位技术进行了对比分析。关于 UWB 定位深度学习的最新研究成果见文献[7-9],这些文献讨论的定位系统有效减小了测距误差和计算负担,以更低的网络复杂度实现了出色的定位性能。也有学者提出了不同的深度学习方法来提高 UWB 定位系统的精度,如使用卷积神经网络 (convolutional neural networks , CNN)来计算标签与基站间的距离[10],使用 CNN 并结合正交频分复用技术和超宽带来识别信道环境[11]。文献[12]中使用 CNN 的定位系统能够在非视距(non line of sight ,NLOS)条件下达到17.3 cm 的平均绝对定位误差。
在以往的研究中,虽然 UWB 室内定位系统的定位效果得到了有效改善,但定位精度仍有很大的提升空间,也未有将 GRU 与超宽带室内定位相结合的先例。因此,有必要提出一种新的基于深度学习的 UWB 室内定位方法。本文将基于深度学习的 GRU 神经网络与 UWB 定位系统相结合,提出了一种全新的 UWB 室内定位方法。实验结果表明,该模型能有效提高 UWB 室内定位精度,减小定位误差。
下面将从 GRU 神经网络的批量大小、优化器、隐藏节点数、学习率、网络层数、损失函数几个方面比较网络中不同参数对 GRU 网络模型性能的影响。通过对模型参数进行多次调整训练,将训练结果的平均值作为最终结果来分析 GRU 模型的性能,证明了 GRU 神经网络与 UWB 室内定位系统相结合的优越性。
1 UWB 定位方法
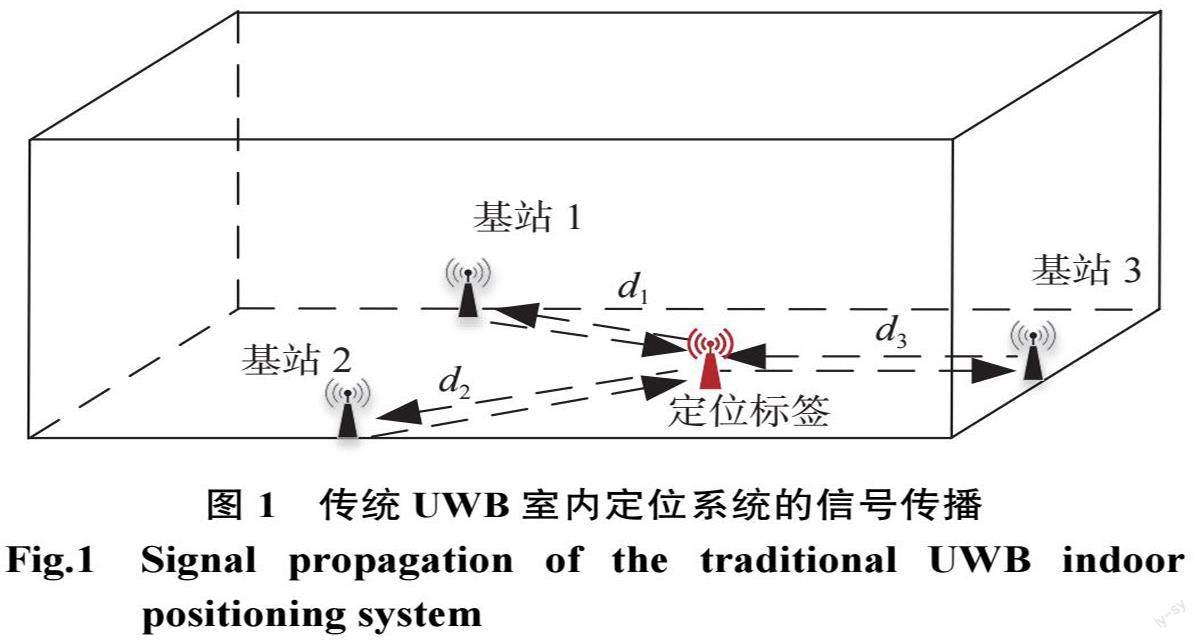
传统的 UWB 室内定位方法常用 TOA 算法来进行位置测算,如图1所示。这种算法通过基站和标签之间的多次通信实现。首先,基站向标签发送信号,并记录基站当前时间,记为Ti1,i 表示基站, i=1,2,3;然后,标签收到基站信号,返回确认信号;接着,基站收到标签的确认信号,记录当前的时间,记为Ti2;最后,基站计算两次信号的时间差Ti = Ti1? Ti2,并以此计算出基站与标签间的距离di = Tic ,c为信号传播速度。在实际应用中,往往会利用多次通信来使测算更加精确。但是, TOA 算法需要基站和标签之间严格的时钟同步,否则无法计算出时间差的精确值,这无疑增加了定位难度。
传统 UWB 室内定位系统在获取标签到基站的距离后,利用三边测量法来计算标签的具体位置。但在实际情况中,由于误差的存在,三边测量法最终的计算结果只能是一个近似值。而根据图灵完备性定理,一个全连接 RNN 可以近似求解所有可计算问题。
因此,为了提高 UWB 系统的室内定位精度,本文使用 GRU 神经网络对定位算法中的误差进行弥补,与传统的 UWB 定位系统相比,基于深度学习的新定位模型将定位算法分配给神经网络模型进行计算,通过训练模型来对最终定位的误差进行弥补。结果表明,本文构建的 GRU 神经网络模型有效地提高了定位精度,将定位误差缩小到很小范围,新定位模型流程图如图2所示。
1.1 三边测量法
三边测量法如图3所示。
图3中,Ri(xi ;yi)与P(xp ;y p)分别为基站与标签的坐标。计算标签到各基站的距离值平方di(2)为
式(1)中, i取值为1, 2, 3, 将上述方程展开,得到:
不妨假设i=1,k=2,3,可以得到一个三元的线性方程组为
通过求解方程组(5)可以得到需预测的标签坐标 P(xp ;y p)。将式(5)看作 Ax = b,线性方程组的 A, x ,b分别为
方程组的解应该使得如下定义的δ最小,δ为
运用最小均方误差(MMSE)方法,可以解得x 为
关于三边测量算法实现的更多细节,可以参考文献[13]。
1.2 门控循环单元网络
1.2.1循环神经网络
对前馈神经网络(feedforward neural network, FNN)而言,信息只进行前向传递,模型的输出依赖于当前的输入。模型较为简单也易于学习,但模型表示能力不足。在很多现实场景中,当前时刻的输出信息不仅依赖于当前时刻的输入信息,也与历史时刻的信息相关。相较而言,循环神经网络(recurrent neural network ,RNN)天然具有处理时序信息的能力,在 RNN 中,神经元在接受当前时刻输入信息的同时,也通过环状的网络结构接收来自上一时刻自身神经元传递过来的信息 ht,如图4所示。这样就构成了输出信息中既包含了当前时刻的输入信息也包含了历史时刻的信息,能够有效增强模型的表示能力。
为了更好地理解 RNN 结构,将 RNN 中的时间序列数据按时刻展开,如图5所示。
由图5可以看出, RNN 的信息传播方式为: t1时刻,输入信息x1与初始状态h0,共同经过非线性激活函数得到当前时刻的隐状态h1,h1经过输出层得到当前时刻的输出y1; h1与t2时刻的输入x2经过非线性激活函数得到隐状态h2, h2经过输出层得到t2时刻的输出y2;依此类推。上一时刻的隐状态hi与下一时刻的输入xi+1共同决定了下一时刻的输出yi+1,由此可以看出 RNN 在处理时序数据上的优越性。
1.2.2循环神经网络的长程依赖问题
在 RNN 中间时刻的状态传播过程中:
式中: zt为中间 t时刻的净输入; U ∈ RD×D为第 t?1时刻隐状态到 t时刻隐状态的权重矩阵; W ∈ RD×D为 t时刻的输入到 t时刻隐状态的权重矩阵; b ∈ RD为偏置向量; f 为非线性激活函数。
因为 RNN 中每个时刻参数共享,所以每个时刻的参数U; W; b和函数f 并无变化。设整个 RNN 序列的损失为L,不失一般性,以对参数U的梯度更
式中:误差项δt;k =表示t时刻的损失Lt对k时刻隐状态净输入zk 的导数; T 表示 RNN 时间序列总共有 T个时刻; t表示中間的某个时刻。所以,式(15)可以写成:
而
将式(17)中的δt;k+1展开,得到:
式中, f ′(zτ)为激活函数导数,通常是有界的。
将每个时刻产生的diag(f ′(zτ))UT近似为相等值(严格来说每个时刻是不等的),则可令γ="diag(f ′(zτ))UT",可得:
理想状态是δ既不太大也不太小,这样能够使得梯度比较稳定。但是,若γ>1,且 t?k →∞ , 则γt?k →∞ , δt;k →∞ , 此时梯度变得很大,称为“梯度爆炸”,造成模型无法学习;若γ<1,且 t?k →∞ , 则γt?k →0,δt;k →0 ,此时梯度变得很小,称为“梯度消失”,造成模型无法学习到长距离时刻的信息。这两个问题统称为 RNN 的长程依赖问题。
1.2.3长程依赖问题的优化方案
简单来说,长程依赖问题就是由于 RNN 在时间维度上比较深,在进行梯度反向传播时,无论梯度是过大还是过小,若t和k的间隔足够大,经过一层层的传播后,连乘使得最终的梯度趋于0或∞。
而 RNN 的梯度爆炸是不难解决的,可通过梯度截断和权重衰减来优化。相对而言,梯度消失是网络中较难解决的问题。由式(18)可以看出,要解决梯度消失问题,就要使得中间项diag(f \(zτ))UT = I,I 为单位矩阵。方法一,通过调参使得diag(f \(zτ))UT = I ;方法二,通过修改模型使得diag(f \(zτ))UT = I。下面介绍方法二。
首先,令式(13)中的非线性变换f 变为线性变换且线性权重为1,结合式(12),得到:
此时 diag(f \(zτ))UT中的 diag(f \(zτ))= I,再令U = I,得到:
则有 diag(f \(zτ))UT = II , ht 和 ht一1之间为线性关系,权重为 1,此时式(19)中的γ=1,即使 t 一 k y 凯,γt一k仍等于1,即不存在梯度爆炸或消失问题。但此时仍应保留ht 和xt之间的非线性关系以保留网络的表示能力,所以对Wxt + b需额外增加非线性激活函数g,则有:
至此,虽然解决了 RNN 的梯度爆炸和梯度消失问题,但由于ht 和ht一1之间只存在线性关系,导致模型表示能力仍会下降。需要重新添加 ht 和 ht一1的非线性关系,即
式中, V为权重矩阵。
此时,因为ht 和ht一1之间既有线性关系也有非线性关系,非线性关系保证了模型的表示能力,线性关系缓解了梯度爆炸和梯度消失的问题。但这样的优化仍存在以下两个问题:
a.梯度爆炸问题。令 zk = Vhk一1+Wxk+ b为第 k个时刻非线性函数g的输入,则在计算式(17)中的δt;k =时,虽然ht 和ht一1之间的线性关系缓解了梯度爆炸问题,若g的值足够大,仍有可能发生梯度爆炸,只是可能性非常小。
b.记忆容量问题。设g为 Logistic 函数,随着时刻 t 的增加, ht一1所包含的信息也在增加, Logistic 函数会达到饱和,趋向于1,导致 ht 中的信息也趋向饱和,无法增加新的信息。
针对上述两个问题,可进一步对模型进行优化,引入门控机制使模型能够主动丢弃一些信息。
1.2.4 门控循环单元网络
为了解决记忆容量的问题,可以在式(23)的基础上引入门控机制来控制 ht 中累计的信息量。 GRU 即是在式(23)的基础上引入了更新门zt e [0;1]D, zt是与ht 维度相同的D维向量。
当 zt的某一维度值为0时,表示将对应维度 ht一1中的信息全部遗忘,只依赖于后面g中新产生的信息。当zt的所有维度值全部为1时,表示ht 的信息全部来自ht一1,和后面新输入的信息xt没有关系。更新门 zt可以表示为 zt =σ(Wzxt + Uz ht一1+ bz ),非线性函数σ可以使用 Logistic 函数。式(24)中的非线性函数g可以使用 tanh 函数,令h(?)t = g(Vht一1+Wxt + b),则有:
若想让ht 只依赖于xt的信息,而和ht一1没有关系,式(25)无法实现。需要另外引入 D 维向量 rt e [0;1]D ,表示为 rt =σ(Wrxt + Urht一1+ br), rt称为重置门,引入rt后, h(?)t 变为 h(?)t = tanh(V(rto ht一1)+Wxt + b),式(24)变为 ht = ztoht一1+(1一 zt) og(V(rtoht一1)+Wxt + b)(26)令zt ,rt皆为零向量,则此时ht 只依赖于xt的信息。
至此,就完成了從 RNN 到 GRU 的模型构造。 GRU 作为 RNN 的一个变种,在保留了 RNN 处理时序数据优势的基础上,解决了长程依赖问题,能够使模型建立长距离时刻的依赖关系。在 UWB 室内定位模型中,每个时刻定位标签的位置坐标不仅依赖于当前时刻定位标签到基站的距离信息,而且也与历史时刻定位标签的位置坐标有一定的关系。建立历史位置信息与当前时刻位置信息的联系能够有助于模型作出更准确的决策。这是本文选择 GRU 网络构建 UWB 室内定位系统模型的主要原因。
1.3 定位模型算法步骤
基于 GRU 网络的 UWB 室内定位模型具体算法步骤如下:
输入基站到标签的距离。
输出 GRU 网络的回归输出。
步骤1 标签沿着预定轨迹移动,随机收集标签在轨迹上的点坐标,并在加入随机误差后计算到各基站的距离,直到收集的数据量足够为止。
步骤2 初始化 GRU 网络参数。
步骤3 将收集到的训练集整理后放入 GRU 网络中进行模型训练(离线计算)。
步骤4 不断调整参数,确定 GRU 网络的最佳参数。
步骤5 确定最佳参数后在验证集上对模型拟合能力进行验证。
2 模型结果的比较与分析
2.1 模型训练及参数选择
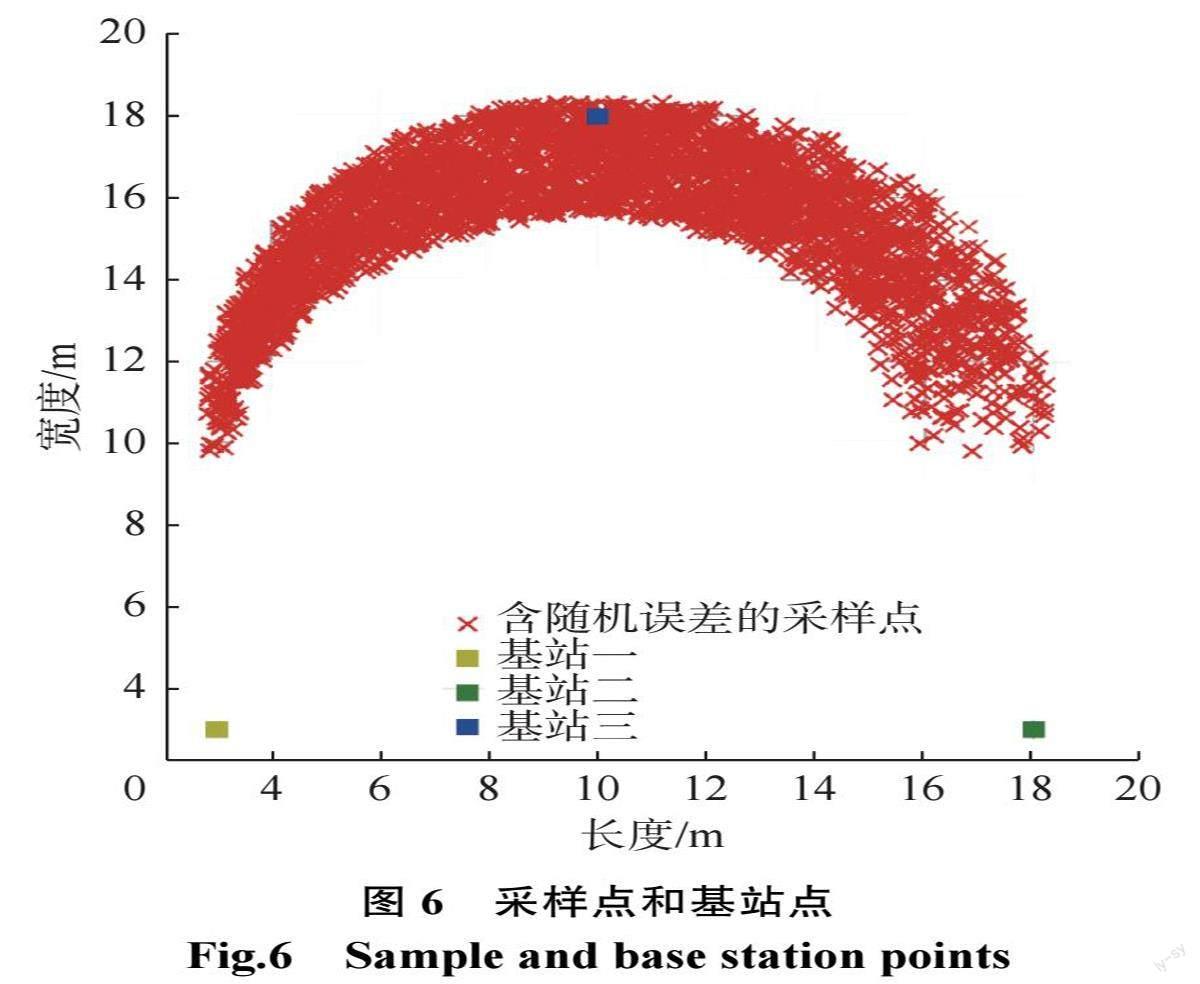
本文使用 Matlab 构建数据环境,使标签沿着上半圆轨迹从坐标(3,10)移动到坐标(17,10)。在此期间,在轨迹上随机选取3000个点,得到点的坐标。然后,在每个样本点的横纵坐标里添加8%以内的随机误差来模拟信号传播过程中的误差。在模拟区域放置基站1(3,3)、基站2(18,3)和基站3(10,18),使用基站坐标和带有随机误差的样本点坐标计算 GRU 网络的3个输入距离值,使用带有随机误差的样本点坐标作为训练集和测试集的对照标签。图6中的正方形代表3个基站,十字代表定位标签移动轨迹上随机选取的3000个点加上随机误差后的坐标。
理论上说,增加基站數量可以增加定位标签到基站的距离信息量,进而增加输入特征的维度,这样可以适当增强模型的表示能力,使得模型更容易拟合数据。但这种促进作用有限,因为3个基站的距离信息已经可以使模型达到高精度。基于缩小成本的原则,本文采用3个基站数。
通过模拟环境,获得3000组样本,其中,70%的样本作为训练集,30%的样本作为测试集。下面分析不同参数下模型的损失值随训练轮数的变化情况。
首先,分析了不同优化器对模型性能的影响,从图7(a)可以看出,在使用 Adam优化器的情况下,模型收敛速度快且平稳。因此,本模型选择的优化器为 Adam。
其次,分析了不同学习率对模型性能的影响,学习率过大可能导致模型产生振荡,学习率过小可能导致收敛缓慢或无法学习。从图7(b)中可以看出,学习率取0.001时,模型在兼顾收敛速度的同时也更加稳定。因此,本模型选择学习率为0.001。
然后,分析了不同批量大小对模型性能的影响。图7(c)显示了不同批量大小下模型损失函数的收敛情况,可以看出,批量越小,模型收敛得越快。但批量不宜过小,否则模型训练时间会大幅增加,不利于模型的实际部署。综合考虑模型的收敛速度、泛化能力和稳定性,本模型选择批量大小为64。
最后,分析了不同数量的隐藏神经元对模型性能的影响。虽然过多的神经元可以增强模型表示能力,但神经元的增加意味着模型复杂度的上升,在提高模型拟合数据能力的同时也会导致过拟合问题。图7(d)显示了在不同隐藏神经元数量下模型损失函数的变化情况,综合考虑之下选择隐藏神经元数量为256个。
而采用不同的网络层数,模型的能力也会有不同的变化。图8显示了不同 GRU 网络层数下模型的平均定位距离误差。从图8中可以看出,随着 GRU 网络层数的增加,模型的平均定位误差也在增加,导致模型性能变差,这是因为过多的网络层数导致了模型的过拟合。且在网络层数增加到5层及以上时,模型的训练轮数及每轮训练时间都会大幅增加。 GRU 网络层数的合理选择也是提高模型性能不可忽视的因素之一,在本文模型中,最适合的网络层数为1层。
本文选择均方误差(MSE)损失函数作为模型的损失函数。因此,根据调整不同参数得到的训练结果,本文选择的各参数值如表1所示。
在确定最优参数后,使用表1所示的参数来验证模型对测试集的效果,并使用平均定位误差 A(模型在测试集上的总误差除以测试集中的样本数量)来观察模型的预测效果。
式中:(xi(p)re ,yi(p)re )为测试集的3个距离值输入到模型后的模型输出值;(xi(t)est ,yi(t)est )为测试集样本的对照标签; n为测试集的样本数,在本文中, n=900。
图9是在使用表1参数值的基础上分别对模型训练20次,每次记录模型在测试集上的预测坐标与实际坐标间的平均距离误差。
通过对模型进行多次训练,计算测试集上的平均误差,可以得到训练后的模型在测试集上的平均误差为6.8 cm。
2.2 不同算法对比
2.2.1前馈神经网络
在 FNN 中,信息传递是由前往后单向传递的,具有以下特性:相邻两层神经元之间全部两两连接;每一层内的神经元之间无连接;信息由前向后单向传递。以第l层为例,信息传递的过程为
z(l)= W(l)d(l?1)+ b(l) (28)
d(l)= fl(z(l)) (29)
式中:第l?1层的输出为d(l?1),d(l?1)∈ RMl?1;经过第l?1层到第l层的权重矩阵为W(l),W(l)∈ RMl×Ml?1;第l?1层到第l层的偏置向量为 b(l) ,b(l)∈ RMl;线性计算后得到第l层的净输入向量为 z(l), z(l)∈ RMl; z(l)经过第l层的非线性激活函数fl得到第l层的输出 d(l),d(l)∈ RMl。整个前馈神经网络可以看成是一个个非线性激活函数的复合。
将上文得到的数据集输入 FNN 中,记录其训练时间、预测时间及精度。
2.2.2长短期记忆网络
长短期记忆网络( long short-term memory network , LSTM)是 RNN 的另一个变体,也是为了解决 RNN 中存在的记忆容量问题而提出的。 LSTM 引入了一个内部状态et ∈ RD用以记录所有历史信息,其信息传递过程为
t = tanh(Veht?1+Wext + be) (30)
et = ft⊙ et?1+ it⊙ t (31)
ht = ot⊙tanh(et) (32)
式(30)中,根据当前时刻的输入xt和上一时刻的隐状态 ht?1计算得出候选状态 t , t ∈ RD。式(31)中,候选状态 t 和上一时刻的et?1分别与it 和ft作元素乘积运算得到当前时刻的 et 。 ft =σ(Vfht?1+ Wfxt + bf)为遗忘门,用以控制遗忘多少上一时刻 et?1中的信息。 it =σ(Viht?1+Wixt + bi)为输入门,用以控制保存多少当前时刻候选状态et的信息。式(32)中,当前时刻的 et经过非线性激活函数 tanh 后与ot作元素乘积运算,得到当前时刻的隐状态 ht , ot =σ(Voht?1+Woxt + bo)为输出门,用以控制输出多少信息给当前时刻的隐状态ht 。ft ; it ; ot的激活函数可以是 Logistic 函数。
将上文得到的数据集输入 LSTM 中,记录其训练时间、预测时间及精度。
2.2.3不同方法对比
GRU 模型的训练和预测时间是判断模型实际是否可行的关键,表2总结了不同深度学习方法在 UWB 室内定位模型上的训练和预测时间。
从表2可以看出,所构建的 GRU 模型在训练时间和预测时间上仍高于 FNN 和 RNN。但是,当考虑到定位精度时,相较于其他深度学习方法与传统 UWB 算法, GRU 在可接受的时间范围内给出了较高的精度。
最终结果表明,本文提出的基于 GRU 神经网络的 UWB 室内定位系统优于其他深度学习方法与传统定位方法,能够为 UWB 室内定位提供更好的定位效果。
3 结束语
在本文的研究中,将 GRU 神经网络应用于 UWB 室内定位,建立了一种新的室内定位方法。该方法以定位标签到基站的距离作为网络的输入,从学习率、优化器、批量大小、网络层数、隐层神经元数量和损失函数6个方面分析了不同参数对模型性能的影响,确定模型的最优参数。最终的模型验证结果表明: GRU 网络用于 UWB 室内定位,其定位精度相较于其他深度学习方法,误差减少了39.82%~81.72%;相较于传统定位算法,误差减少了66.00%~92.44%。因此,随着深度学习技术的成熟,神经网络的应用将更加广泛。
参考文献:
[1]王甘楠, 田昕, 魏国亮, 等.基于 RNN 的多传感器融合室内定位方法[J].计算机应用研究 , 2021, 38(12):3725–3729.
[2]黄瑞贞.非线性最小二乘超宽带 TOA 法在室内定位测量中的研究与实现[J].测绘与空间地理信息 , 2020, 43(4):214–217,224.
[3]周军, 魏国亮, 田昕, 等.融合 UWB 和 IMU 数据的新型室内定位算法[J].小型微型计算机系统 , 2021, 42(8):1741–1746.
[4]李景文, 韦晶闪, 周俊芬, 等.融合 UWB+PDR 的室内定位方法改进[J].测绘通报, 2022(3):36–40.
[5]刘韬 , 徐爱功 , 隋心.基于自适应抗差卡尔曼滤波的 UWB 室内定位[J].传感技术学报, 2018, 31(4):567–572.
[6]孙大洋, 章荣炜, 李赞.室内定位技术综述[J].无人系统技术, 2020, 3(3):32–46.
[7] HSIEH C H, CHEN J Y, NIEN B H. Deep learning-based indoor localization using received signal strength and channel state information[J]. IEEE Access, 2019, 7:33256–33267.
[8] MEGHANI S K, ASIF M, AWIN F, et al. Empirical based ranging error mitigation in IR-UWB: a fuzzy approach[J]. IEEE Access, 2019, 7:33686–33697.
[9] XUE Y, SU W, WANG H C, et al. DeePTAL: deep learning for TDOA-based asynchronous localization security with measurement error and missing data[J]. IEEE Access, 2019, 7:122492–122502.
[10] JOUNG J, JUNG S, CHUNG S, et al. CNN-based Tx–Rxdistance estimation for UWB system localisation[J]. Electronics Letters, 2019, 55(17):938–940.
[11]王斐 , 徐湛 , 职如昕 , 等.基于卷积神经网络的 OFDM- UWB 信道环境识别[J].计算机工程 , 2021, 47(7):161–167.
[12] NIITSOO A, EDELH?U?ER T, MUTSCHLER C. Convolutional neural networks for position estimation in TDoA-based locating systems[C]//Proceedings of 2018 International Conference on Indoor Positioning and Indoor Navigation. Nantes: IEEE, 2018:1–8.
[13] POULOSE A, KIM J, HAN D S. A sensor fusion framework for indoor localization using smartphone sensors and wi-firssi measurements[J]. Applied Sciences, 2019, 9(20):4379.
(编辑:丁红艺)

