用于实现医学图像对比度增强的密文域可逆信息隐藏算法
李安 周亮 张建青 陈立范 周艳丽 王宏杰 孔平

摘要:针对现有密文域医学图像可逆信息隐藏算法存在解密图像视觉质量较低的问题,提出了一种基于差值直方图平移的密文域可逆信息隐藏算法。首先,发送方采用具有同态密文比较性质的加密算法对原始医学图像进行加密,从而保证医学图像的隐私内容不被泄露。然后,嵌入方利用同态性质对接收到的密文图像计算差值直方图,并通过平移差值直方图在密文图像中嵌入信息。為了获得较大的嵌入率,嵌入方可对密文图像进行多轮次信息嵌入。最后,接收方根据拥有的密钥种类对接收到的含有嵌入信息的密文图像进行信息提取、图像解密和图像恢复。实验结果表明,本文算法提升了解密医学图像的视觉质量,同时具有较高的嵌入率和安全性。
关键词:可逆信息隐藏;医学图像;直方图平移;同态加密;图像对比度增强
中图分类号:TP 309.7 文献标志码:A
Reversible data hiding method in encrypted domain for the contrast enhancement of medical image
LIAn1, ZHOU Liang2, ZHANG Jianqing3, CHEN Lifan4, ZHOU Yanli4, WANG Hongjie4, KONG Ping2
(1. School of Health Science and Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China; 2. Collaborative Innovation Center, Shanghai University of Medicine and Health Sciences, Shanghai 201318, China;3. College of Medical Imaging, Shanghai University of Medicine and Health Sciences, Shanghai 201318, China;4. College of Arts and Science, Shanghai University of Medicine and Health Sciences, Shanghai 201318, China)
Abstract: Aiming at the problem that the visual quality of the decrypted image is low in the existing reversible data hiding methods for the encrypted medical image, a reversible data hiding method in encrypted domain based on the difference histogram shift was proposed. Firstly, to ensure that the private content of the medical image was not leaked, the sender using an encryption algorithm with the property of homomorphic ciphertext comparison encrypted the original medical image. Then, on the data-hider side, the difference histogram of the received encrypted image was calculated using the homomorphic property, and the secret data was embedded in the encrypted image by shifting the difference histogram. In order to obtain a high embedding rate, the data-hider could conduct multiple rounds of data embedding in the encrypted image. Finally, according to the type of the keys possessed, the receiver could perform data extraction, image decryption and image recovery for the received encrypted image containing embedded data. The experimental results show that the proposed method improves the visual quality of the decrypted medical image, and has high embedding rate and security.
Keywords:reversible data hiding; medical image;histogram shift; homomorphic encryption; image contrast enhancement
随着远程医疗、智慧医疗和云医疗的飞速发展,医学图像的隐私保护与内容认证越来越重要。密文域可逆信息隐藏作为一种隐私保护技术受到了广泛的关注。该技术能够向加密的载体图像嵌入一段额外信息,在解密图像中难以察觉嵌入信息的存在,在提取嵌入信息后可逆恢复载体图像。
Zhang[1]提出了一种经典的密文域可逆信息隐藏算法,它通过翻转密文块中部分像素的最低3位有效位来嵌入信息。该算法的嵌入率低,在信息提取和图像恢复过程中存在一定的错误率。近几年,学者们提出了很多先进的密文域可逆信息隐藏算法。如 Fu等[2]提出了一种基于自适应编码策略的密文域可逆信息隐藏算法,它根据最高有效位出现的频率,自适应地压缩可嵌入块的最高有效位比特层来腾出空间容纳嵌入信息。该算法有较好的率失真性能和较高的嵌入率。 Qiu 等[3]提 出了一种基于自适应整数变换的密文域可逆信息隐藏算法,它通过可逆的整数变换去除像素的最低有效位,并将信息嵌入在像素的最低有效位,该算法有较高的嵌入容量。 Yu 等[4]提出了一种新颖的密文域可逆信息隐藏算法,可以在无需知道加密方法或原始图像先验知识的前提下,通过简单的最高有效位替换将额外信息嵌入到加密图像中。但是这些算法均是针对自然图像设计的,不适用于医学图像。因此,医学图像的隐私安全问题亟需设计专门的算法。
Bhardwaj 等[5]提出一种密文域医学对偶图像可逆信息隐藏算法。该算法为了提高医学图像的嵌入率,将嵌入的信息转换为 base-3数字框架来解决零值不嵌入问题。 Kong 等[6]提出了一种具有篡改定位功能的密文域医学图像可逆信息隐藏算法。为了提高医学图像恢复的准确率,该算法只在加密图像的部分区域嵌入信息。由于其嵌入信息的方式与 Zhang[1]的算法类似,在信息提取和图像恢复过程中会存在一定的错误率。由于大多数医学图像是16位的灰度图像, Dzwonkowski 等[7] 提出了一种基于循环二进制 Golay(23,12)码的密文域医学图像可逆信息隐藏算法。该算法在加密图像的最低有效位中嵌入额外信息,而最高有效位被用于确保嵌入过程的可逆性。付笛等[8]利用医学图像像素深度高、像素分布连续性高的特点,提出了一种结合两种压缩算法的密文域可逆信息隐藏算法。该算法通过两种压缩算法分别对加密图像的高位比特层和低位比特层进行压缩,从而腾出空间容纳嵌入信息。但是这些算法都存在解密医学图像视觉质量下降的问题。
为了提升解密后医学图像的视觉质量,本文提出了一种基于差值直方图平移的密文域医学图像可逆信息隐藏算法。在该算法中,信息的嵌入不仅使解密医学图像具有对比度增强的效果,且该算法是完全可逆的,即信息提取和图像恢复的错误率为0,同时算法嵌入的信息量越大,医学图像的对比度增强效果越显著。实验结果表明,本文算法具有较高的嵌入率、解密图像质量和安全性。
1 本文算法
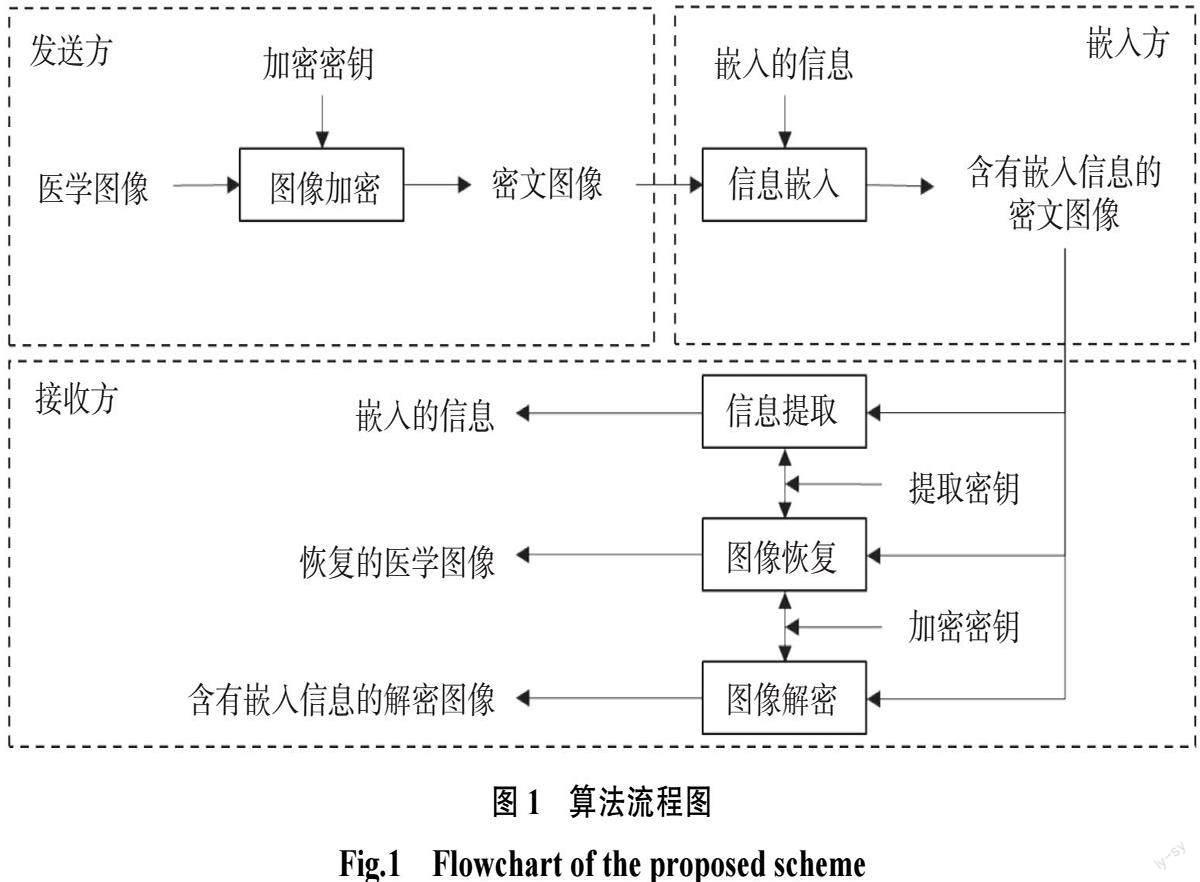
算法流程如图1所示。下文将详细阐述算法的图像加密、信息嵌入、信息提取和图像恢复等内容。
1.1 图像加密
為了保护医学图像的隐私,本文采用一种具有同态密文比较性质的同态加密算法[9]对医学图像进行加密。该同态加密算法基于共轭搜索问题来实现单向安全,支持矩阵环上的实数加密。
假设R是一个实数域,Ψ是R上一个2×2的矩阵环。发送方利用加密密钥Ke ={K 1); K 2)}分别生成一个随机的可逆矩阵H和一个扰动矩阵R:
( H = (1)
式中,h1; h2;···; h9∈Ψ, 且r1; r2;···; r9∈Ψ。h1; h2;···; h9和 r1; r2;···; r9都是2×2的矩阵。由此可见, H和 R都是6×6的矩阵。
定义大小为 U × V的医学图像为 I。假设 I中(i; j)位置上像素的灰度值为Ii;j 。发送方对I进行加密就是利用矩阵H和R将I中每个像素的灰度值都加密成一个密文。发送方首先将I中每个像素的灰度值 Ii;j 随机拆分成6个不为0的值 m1,m2,m3, m4,m5,m6,其中, m1> m2,m3> m4,m5> m6,且Ii;j = m1+m2= m3+ m4= m5+ m6。然后,用这6个 值生成3个2×2的矩阵M1; M2; M3:
最后,用矩阵H和R将这3个矩阵 M1; M2; M3加密成密文Ei;j:
式中: E(·)为加密函数; n1; n2; n3均是从Ψ中随机挑选的; O为2×2的全零矩阵。
当将I中所有像素的灰度值都加密成密文后,收集所有密文,生成密文图像E。需要强调的是, Ei;j 是由 Ii;j 加密而成的密文,不是单个值,而是6×6的矩阵。因此, Ei;j 也不是对E中(i; j)位置上单个值的索引,而是对E中(i; j)位置上密文的索引。图2为密文图像中密文索引的示例。
此外,发送方用随机矩阵H生成一个用于同态密文比较的公开矩阵T:
式(5)中, n4; n5; n6也均是从Ψ中随机挑选的,并生成一个用于平移差值直方图的偏移子σ= E (1)。需要说明的是, T和σ是公开的,即发送方、嵌入方和接收方都知晓。最后,发送方将密文图像E发送给嵌入方。
1.2 信息嵌入
嵌入方接收到密文图像E后,将E分成(UV)/9个不重叠密文块B(1); B(2);···; B((UV)/9)。每个密文块 B(l)(l =1;2;···;( UV)/9)内有9个密文,每行每列各3个密文,如图3所示。
由图3可知,每个密文块B(l)内都有1个中心密文Ei;j 和8个周边密文。对于每个密文块B(l),嵌入方根据式(7)计算8个差值:
其中,Ei;j?1,Ei?1;j,Ei;j+1,Ei+1;j,Ei?1;j?1,Ei?1;j+1,Ei+1;j?1和Ei+1;j+1都是B(l)内的周边密文,并且计算出来的差值也都是密文,即6×6的矩阵。
当计算了所有密文块内的差值后收集所有差值,生成差值序列(Du1;v1; Du2;v2;···; Du s ;vs),其中, s =(8UV)/9。嵌入方可以用公开矩阵T计算任意两差值Du1;v1与Du2;v2之间的 t 值: t =Γ(Du1;v1; Du2;v2)= det (Du1;v1? T · Du2;v2)(8)式中: det(·)为计算方阵行列式的函数;Γ(·;·)是同态密文比较函数。
根据同态加密算法[9]的同态密文比较性质, t 值的符号与D(Du1;v1)? D(Du2;v2)的符号始终保持一致:
式中, D(·)为解密函数,将在下文进行介绍。
同态密文比较性质的证明详见文献[9]。由此可见,嵌入方可以利用同态密文比较性质在未解密任何差值的情况下得知任意两差值之间的大小关系。因此,嵌入方可以对差值序列(Du1;v1; Du2;v2;···; Du s ;vs)进行由小到大的排序,生成排序后的差值序列(D(一)u1;v1; D(一)u2;v2;···; D(一)us ;vs)。
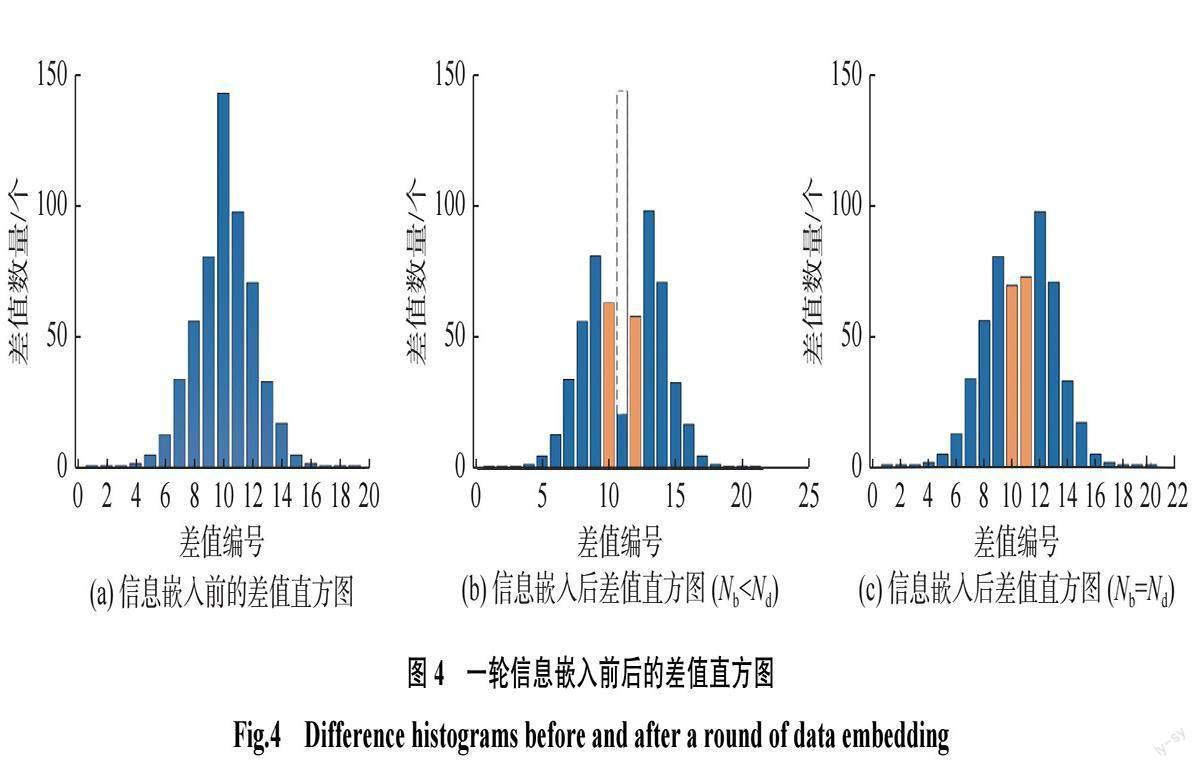
为了生成差值直方图,嵌入方对(D(一)u1;v1;D(一)u2;v2;···; D(一)us ;vs)中的每个差值进行编号。第一个差值的编号f(D(一)u1;v1)=1,而后续的每个差值D(一)uz ;vz(2< z < s)都需要与前一个差值D(一)uz?1;vz?1进行同态密文比较。若Γ(D(一)uz ;vz ; D(一)uz?1;vz?1)=0,该差值的编号f(D(一)uz ;vz )= f(D(一)uz?1;vz?1),否则f(D(一)uz ;vz )= f(D(一)uz?1;vz?1)+1。此时,嵌入方对所有差值的编号进行统计,生成 差值直方图,如图4(a)所示。从图4(a)中可 知,生成的差值直方图会在某一差值编号出现峰值,而下文将利用此峰值向密文图像中嵌入信息。
假设所有差值的编号中数量最多的编号为f (D(一)u一z;v一z),z(一)∈[1; s]。嵌入方以光栅的顺序扫描密文图像E中每个密文块B(l)内的每个差值Du;v ,并执行以下操作来平移差值直方图,从而嵌入信息:
式(10)中:f(·)为差值到编号的映射函数;ξ(·)为符后的密文(号函数;)用来替换E(为嵌入的二)u;v(进) u;v为由Eu;v更新
最后,用更新后的密文替换密文图像 E 中相应的密文,生成含有嵌入信息的密文图像 E(1),而值数量为Nd(信息提取密)1述)=一Db 信息嵌入最(若编号为f);密(的)文(差)图像 E 中嵌入Nd个比特的信息。
假设需要嵌入信息的 bit 数为 Nb。若 Nb< Nd,嵌入方只需要执行一轮信息嵌入就能将所有信息嵌入在密文图像 E 中。图4显示了一轮信息嵌入前后差值直方图的变化。从图4(a)到(b)的变化可知,当Nb< Nd时,信息嵌入后的差值直方图中新生成了两个柱体(图4(b)中橙色柱体),差值编号的总数量增加了2个。图4(a)中为峰值的差值编号在图4(b)中增大了1个单位且仍有剩余差值数量。从图4( a)到( c)的变化可知,当 Nb = Nd时,信息嵌入后的差值直方图中同样新生成了两个柱体(图4(c)中橙色柱体),但差值编号的总数量只增加了1个。因为图4(a)中为峰值的差值编号全部被用于信息的嵌入,剩余的差值数量为0。若Nb> Nd,嵌入方先执行一轮信息嵌入,向 E 中嵌入Nd个 bit 的信息,再对 E(1)执行新一轮的信息嵌入。对 E(1)执行一轮信息嵌入同样包括上述的5个步骤,即分割密文块、计算差值、排序和编号差值、生成差值直方图、平移差值直方图。对 E(1)执行完一轮信息嵌入后,若仍有剩余的信息未被嵌入,嵌入方继续对新生成的含有嵌入信息的密文图像 E(2)进行新一轮的信息嵌入。如此反复,直到完成所有信息的嵌入,生成最终的含有嵌入信息的密文图像E(τ),并收集每一轮信息嵌入生成的信息提取密钥Ka ={K 1); K 2);···; K τ)},其中,τ是信息嵌入的轮数。最后,嵌入方将含有嵌入信息的密文图像E(τ)发送给接收方。
1.3 信息提取和图像恢复
仅拥有加密密钥Ke ={K 1); K 2)}的接收方在接收到含嵌入信息的密文图像 E(τ)后,可通过对 E(τ)解密来获知图像的内容。首先,用K 1)和K 2)分别生成矩阵H和R;然后,用H和R对E(τ)中每个密文E 进行解密,如式(12)所示;最后,收集所有密文的解密结果,生成含有嵌入信息的解密图像 I(τ)。
式中: D(·)是解密函数;[·]1;1和[·]1;2分别表示矩阵中(1;1)和(1;2)位置上的元素; I 是E 解密后的像素值。由于信息的嵌入,相比于原始医学图像I,含有嵌入信息的解密图像I(τ)中相邻像素之间灰度差异更大,视觉上I(τ)的对比度更强。
仅拥有信息提取密钥Ka ={K 1); K 2);···; K τ)}的接收方接收到含嵌入信息的密文圖像E(τ)后,可以从E(τ)中提取出所有嵌入的信息。接收方从提取密钥中元素的个数可以得知信息嵌入的轮数为τ。为了提取所有嵌入的信息,接收方同样需要τ轮信息提取。每轮信息提取都包括分割密文块、计算差值、提取信息、恢复差值直方图等4个步骤。分割密文块和计算差值的两个步骤与前文一致。在执行第1轮信息提取的过程中,接收方以光栅顺序扫描E(τ)中每个密文块内的每个差值 Du;v ,并用信息提取密钥K τ)执行以下操作来提取信息:
同时,执行以下操作来恢复差值直方图:
= E(E) ;?σ; 其他(t2>0) (14)
式中:t1=Γ(Du;v ; K τ)?σ);t2=Γ(Du;v ; K τ)+σ);b′为用来替(提取的)换(二)信息; 为由 E 更新后的密文,
最后,用更新后的密文替换密文图像E(τ)中相应的密文,生成信息提取后的密文图像E(τ?1)。若τ>1,接收方用K τ?1)继续对E(τ?1)执行新一轮的信息提取,直到用完所有信息提取密钥。在执行完τ轮信息提取后,接收方可以准确地提取出所有嵌入的信息,并得到不含嵌入信息的密文图像E(0)。
拥有信息提取密钥Ka 和加密密钥Ke 的接收方在接收到含嵌入信息的密文图像E(τ)后,先用Ka对 E(τ)执行τ轮信息提取,得到提取的信息和不含嵌入信息的密文图像E(0);再用Ke 分别生成矩阵H和 R,并用矩阵H和R根据式(12)对E(0)进行解密,得到与原始医学图像I完全相同的恢复图像I(0)。
2 实验结果与分析
本文实验环境为2.60GHz Intel i7处理器、8.00 GB 内存、 Windows 10操作系统,算法应用 Matlab R2018b 进行实现。实验选取 DICOM( digital imaging and communications in medicine)图像库[10] 中4张典型的512×512 CT(computed tomography)图像,如图5所示。以下从安全性、嵌入率、对比度增强效果3个方面对实验结果进行分析。
2.1 安全性分析
图6给出了图5中4张原始图像加密后的图像。从图6中可以看出,无法从加密后的图像中获取原始图像内容。
2.1.1密文图像相关性分析
相关性分析是分析图像中相邻像素之间的相关性程度。一个安全性高的图像加密算法应该尽可能地破坏原始图像中相邻像素之间的相关性。表1给出了图5中4张 CT 图像加密前后图像在水平、垂直、对角线和反对角线4个方向上的平均相关性系数。从表1中可以看出,加密前图像的平均相关性系数都接近于1,表明原始图像中相邻像素之间存在较强的正相关性。加密后图像的平均相关性系数接近于0,表明密文图像中相邻像素之间的相关性弱,证明了本文算法具有较高的安全性。
2.1.2密文图像差分分析
差分分析是一种密码学领域常用的选择性明文攻击。该攻击将原始图像中的任意一个像素的值改变一个单位,使用相同的加密密钥分别对篡改前后的图像进行加密,通过分析篡改前后密文图像的变化来破译加密密钥。因此,抵抗这种攻击的能力取决于篡改前后密文图像中变化的随机性。像素数变化率 NPCR(number of pixels changing rate)[11]和统一平均变化强度 UACI(uniform average change intensity)[12]被用来分析篡改前后密文图像的变化。NPCR 和 UACI 分别表示篡改前后密文图像之间的变化像素数和平均变化强度数,它们相应的理论值分别为99.6094%和33.4635%。表2给出了图5中4张 CT 图像篡改前后密文图像之间的 NPCR 和 UACI。从表2可以看出,4张图像的 NPCR 和 UACI 都接近相应的理论值99.6094%和33.4635%,证明本文算法对差分分析具有较强的抵抗能力。
2.2 嵌入率和解密图像对比度分析
嵌入率是指嵌入信息量与图像像素总数的比值,表示图像中每个像素被嵌入的平均信息量,单位为 bpp(bits per pixel)。嵌入率越大,图像可嵌入的比特数量越大。图像对比度 IC( image contrast)是指图像中相邻像素灰度差异大小。差异越大,视觉上明暗对比越明显。图像对比度可以通过式(15)来计算。
式中:ε为由图像中所有一阶相邻像素对组成的集合;〈p; q〉为集合ε中一个相邻像素对;Ⅱ·Ⅱ为集合中元素的总数量; w(·)为像素到灰度值的映射函数。由此可见,图像中相邻像素之间的灰度差异越大,计算得到的 IC 越大。
图7给出了图5中4张 CT 图像在不同嵌入轮数n下,嵌入率和含有嵌入信息的解密图像对比度 IC。由图7可知,信息嵌入的轮数越多,嵌入率越大,图像可以被嵌入的信息量越多,含有嵌入信息的解密图像的对比度也越大。图8显示了图5中的4张 CT 圖像20轮信息嵌入后含有嵌入信息的解密图像。从图8可以发现,相比于图5中的原始图像,含有嵌入信息的解密图像在对比度上有明显的增强效果。因此,本文算法能改善解密医学图像的视觉质量。
2.3 丢包现象对算法有效性的影响
在复杂网络环境下,数据有可能存在丢包现象。因此,含有嵌入信息的密文图像在传输过程中可能丢失部分密文。在实验过程中,利用本文算法仅执行1轮信息嵌入,在图6的4张加密 CT 图像中分别嵌入尽可能多的信息,生成4张含有嵌入信息的密文图像。图9给出了含有嵌入信息的密文在密文图像中的位置。图9中,红色标记出了含有嵌入信息的密文在密文图像中的位置,黄色标记出了含有嵌入信息密文块的中心在密文图像中的位置,绿色标记出了不包含嵌入信息的密文在密文图像中的位置。
若丢失了密文图像中含有嵌入信息的密文,该密文所含的嵌入信息将丢失;若丢失了密文图像中含有嵌入信息的密文块的中心密文,该密文块内所含的所有嵌入信息都将丢失;若丢失了密文图像中不包含嵌入信息的密文,则不会影响本文算法的有效性。图9中,4张图像中绿色像素的占比分别为95.23%,95.98%,93.10%,94.51%。因此,当丢包率为0.01%时,发生嵌入信息丢失的概率分别为71.97%,65.60%,84.43%,76.95%。综上所述,含有嵌入信息的密文图像在传输过程中丢失部分密文很大概率会导致相应嵌入信息的丢失。
3 结论
提出了一种基于差值直方图平移的医学图像可逆信息隐藏算法。在该算法中,通过同态加密算法对医学图像的每个像素进行加密来保护医学图像的隐私内容,通过多轮差值直方图平移可以在密文图像中嵌入更多信息。由于信息的嵌入,解密图像中相邻像素之间的灰度差异增大,可有效增强图像的对比度,提升图像视觉质量,并且嵌入的信息越多,解密图像的对比度增强效果越显著。此外,根据信息提取密钥和加密密钥,本算法可以完全恢复原始图像。
参考文献:
[1] ZHANG X P. Reversible data hiding in encrypted image[J]. IEEE Signal Processing Letters, 2011, 18(4):255–258.
[2] FU Y J, KONG P, YAO H, et al. Effective reversible data hiding in encrypted image with adaptive encoding strategy[J]. Information Sciences, 2019, 494:21–36.
[3] QIU Y Q, QIAN Z X, ZENG H Q, et al. Reversible data hiding in encrypted images using adaptive reversible integer transformation[J]. Signal Processing, 2020, 167:107288.
[4] YU M J, YAO H, QIN C. Reversible data hiding in encrypted images without additional information transmission[J]. Signal Processing: Image Communication, 2022, 105:116696.
[5] BHARDWAJ R, AGGARWAL A. Hiding clinical information in medical images: an encrypted dual-image reversible data hiding algorithm with base-3 numeral framework[J]. Optik, 2019, 181:1099–1112.
[6] KONG P, FU D, LI X R, et al. Reversible data hiding in encrypted medical DICOM image[J]. Multimedia Systems, 2021, 27(3):303–315.
[7] DZWONKOWSKI M, RYKACZEWSKI R. Reversible data hiding in encrypted DICOM images using cyclic binary golay (23, 12) Code[J]. IEEE Access, 2021, 9:60503–60515.
[8]付笛, 孔平, 周亮, 等.一种密文域医学图像可逆信息隐藏算法[J].上海理工大学学报, 2022, 44(3):262–268.
[9] LI J, KUANG X H, LIN S J, et al. Privacy preservation for machine learning training and classification based on homomorphic encryption schemes[J]. Information Sciences, 2020, 526:166–179.
[10] GOLDGOF D, HALL L, HAWKINS S, et al. QIN LUNG CT[DB/OL]. [2021-01-15]. https://doi.org/10.7937/K9/ TCIA.2015.NPGZYZBZ.
[11] CHEN G R, MAO Y B, CHUI C K. A symmetric image encryption scheme based on 3D chaotic cat maps[J]. Chaos, Solitons & Fractals, 2004, 21(3):749–761.
[12] MAO Y B, CHEN G R, LIAN S G. A novel fast image encryption scheme based on 3D chaotic baker maps[J]. International Journal of Bifurcation and Chaos, 2004, 14(10):3613–3624.
(編辑:丁红艺)

