飞机荷载引起隧道地表沉降数值模拟研究
邵俐 李闯 蒙强 李佩青
摘要:为研究飞机起飞对隧道施工过程中地表沉降的影响,依托某机场隧道工程实例,利用MIDAS GTS NX软件进行数值模拟,分析了飞机荷载对单线隧道和双线隧道地表沉降的影响规律。研究结果表明,飞机由单线隧道左侧滑行至右侧时,地表沉降最大值由左侧移至中间偏右位置,且最大值不断增大。飞机滑行经过双线隧道工程上方时,地表沉降最大值由先行隧道上方逐渐转移至后行隧道上方;当飞机经过两隧道中间滑行至后行隧道拱肩上方时,地表沉降值最大且超过30mm。单线隧道和双线隧道的最大沉降均位于拱顶位置处,向周围方向沉降值逐渐减小,因此,在施工过程中,除了应定时进行监测外,需重点关注拱顶处沉降情况,保证施工安全。
关键词:飞机荷载;单线隧道;双线隧道;地表沉降;数值模拟
中图分类号:U455;TU 433 文献标志码:A
Numerical simulation study on tunnel surface subsidence caused by aircraft load
SHAO Li1, LI Chuang1, MENG Qiang2, LI Peiqing1
(1. School of Environment and Architecture, University of Shanghai for Science and Technology, Shanghai 200093, China;2. Construction Project Headquarters of Guangxi Airport Management Group, Nanning 530034, China)
Abstract: This study investigated the impact of aircraft take-off on the surface subsidence during the construction of an airport tunnel project with the numerical simulation. The change rule of surface subsidence of single-track tunnel and double-track tunnel caused by the aircraft position under plane load was analyzed through MIDAS GTS NX software. The results demonstrated that, the surface subsidence in a single-track tunnel moved from the left side to the middle of the right side when an aircraft glided from left to right and the maximum value of surface subsidence continued to increase. In the double-track tunnel, the maximum surface subsidence gradually transferred from the top of the first tunnel to the top of the followed tunnel. When the aircraft load was positioned above the arch shoulder of the tunnel behind and passed through the middle of two tunnels, the maximum surface settlement value exceeded 30 mm. The maximum settlements of both single-track and double-track tunnels were located at the vault, with a gradual decrease in settlement value towards the surrounding areas. Those findings suggest that regular monitoring of the construction is essential to ensure the safety during the construction process, especially for the settlement of the vault.
Keywords: plane load; single-track tunnel; double-track tunnel; surface subsidence; numerical simulation
近年來,随着我国经济社会的不断发展,隧道、地铁、桥梁及机场等工程处于高速发展阶段,在机场修建改造过程中,面临隧道下穿飞机跑道的复杂工程。在现有机场下设置隧道,飞机起飞将对隧道施工的安全稳定带来一定影响;在隧道施工工程中,土体的开挖卸载会引起围岩发生应力重分布,进而引起地层损失和地层位移,使得地表发生沉降和变形[1],而机场跑道对于地面的变形、平整度要求格外严格。因此,在隧道施工和飞机荷载的同时作用下会产生耦合作用,工程现场对控制地表沉降提出了更高的要求。为保证施工和飞机起飞的安全进行,对隧道开挖过程中引起的地表沉降进行合理有效的预测是至关重要的。
Wei[2]对深层土体沉降计算方法进行了研究,改进了姜忻良等[3]和孙玉永等[4]的计算公式,得到沉降槽宽度与深度之间的关系,提出了计算双线盾构隧道不同深度处的沉降公式。唐正等[5] 根据上海市田林路下穿中环隧道工程实例,分析了在管幕法群管顶进施工过程中地表沉降的变化规律。鲍先凯等[6]采用三维有限元数值模拟软件 MIDAS GTS 对花椒箐隧道的实际情况进行了模拟,并分析了3种不同施工工法的地表沉降情况,将模拟结果与现场监测结果进行比对,为今后类似情况的隧道工程提供一定的参考。Ding 等[7] 通过数值模拟分析了在隧道施工中下穿已有建筑物的地基基础形式、建筑物刚度、建筑物与隧道之间的角度、建筑物中轴线到隧道中轴线之间的距离对路面沉降的影响。范雨等[8]依托广州地铁某区段的双线盾构隧道,建立了三维有限元模型,研究双线隧道开挖过程中隧道间距对地表沉降的变化规律,分析发现,当隧道间距在1.5D~3D 范围内(D 为隧道直径)变化时,沉降曲线由 V 型到底部较平的 V 型再到 W 型。郑爱元[9]利用 FLAC 3D 模拟软件研究了小净距双线隧道施工所引起的地表和衬砌结构变形情况,并对比实际监测结果,得出小净距施工会使上部地层的沉降增大且衬砌偏压比较严重。丁振义[10]运用 MIDAS GTS NX 有限元分析软件,根据实际工程模拟了3个不同区段的隧道施工,结果表明,先行隧道引起的沉降量占总沉降量的50%左右,其对地表沉降的影响较大,且当双线隧道的间距较小时,其地表沉降曲线为单峰型,同时最大沉降点靠近先行隧道一侧。牟天光等[11]将数值分析方法得到的结果与监测数据相结合,对双线盾构隧道施工横向地表沉降规律进行分析,结果表明,沉降槽呈 V 型且先行隧道一侧的地表沉降量最大。桂登斌等[12]以天府机场工程为背景,通过数值模拟得出飞机滑行至明挖隧道最大回填高度时,地表沉降最大,同时当飞机滑行至隧道正上方时,拱底处隧道结构受力的安全系数最小。魏晓刚等[13]建立了 A380-800飞机六自由度数学模型,利用有限元数值模型分析了在飞机荷载作用下道面?土层?隧道结构的动力响应及影响因素,结果表明,飞机荷载的冲击效应对土体?隧道的结构整体稳定性影响较小,飞机荷载作用位置不同,隧道结构变形变化较大。王志新等[14]依托穗莞深城际铁路隧道下穿深圳宝安国际机场工程,得出在飞机荷载作用下土体任意深度处的附加应力公式以及不同土体埋深情况下3种大型飞机荷载对飞行区盾构隧道影响范围的计算公式。张召峰等[15]依托长沙黄花机场东延线接入 T3航站楼工程,通过理论计算对比了5种不同机型,得出空客 A380-800机型飞机动载引起土体的附加应力最大,并通过对比分析得出覆土深度与飞机荷载引起的附加应力呈反比关系。刘凯等[16]以成自高铁下穿天府机场东二跑道的区间隧道工程为背景,通过数值分析方法研究在上方飞机降落冲击荷载作用下高铁隧道衬砌结构的疲劳寿命以及衬砌结构抗减振问题,研究表明, B747-400型飞机在单次重着陆过程中,高铁隧道的衬砌位移峰值、附加第一主应力峰值、附加第三主应力峰值均出现在拱顶位置处。
目前国内外研究主要涉及到单双线隧道在静荷载作用下的沉降变化以及飞机荷载对隧道结构的影响,较少研究飞机荷载滑行时的振动及隧道施工过程中共同耦合作用对隧道地表沉降的影响。本文以南崇铁路引入某机场隧道工程为例,通过有限元软件 MIDAS GTS NX 建立三维模型,分析了无飞机荷载和飞机所处不同位置时对单双线隧道地表沉降的影响规律。
1 工程概况
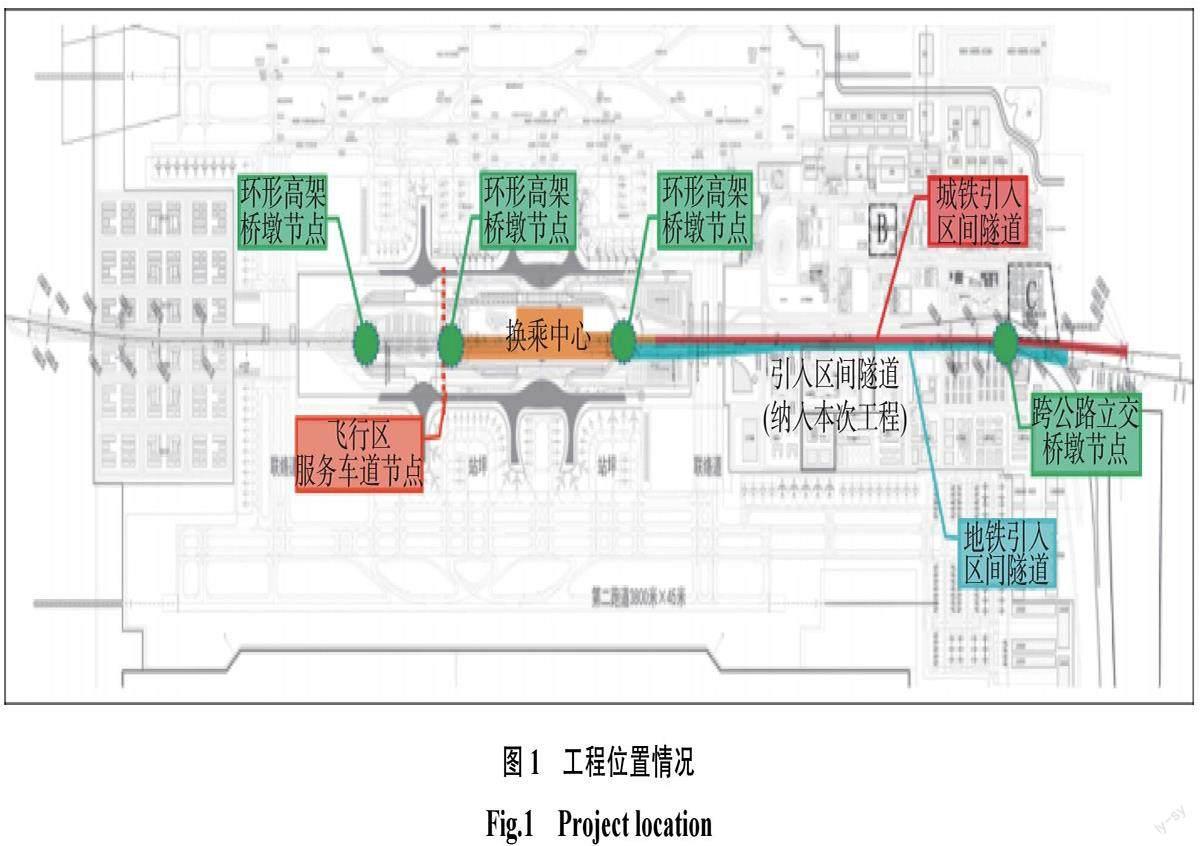
某机场隧道工程由机场站(地下车站)、进口区间隧道组成,全长4535 m,工程位置情况如图1所示。工程场地地面高程约在110~140 m 之间,隧道埋深相应高程约为10~19 m。施工区段场地区土层主要包括1-2素填土(Q4ml)、1-5碎石土(Q4ml)、9-2强风化层(J1w)、9-3中风化层(J1w)。
2 有限元模型建立
选用有限元软件 MIDAS GTS NX 建立隧道施工模型。将各土层简化为均匀土层,各土层土体物理力学参数如表1所示。模拟数值模型土体边界距离隧道中线取3~5倍洞径,隧道断面尺寸如图2所示,选取单隧道模型尺寸为100 m×70 m×35 m ,双隧道模型尺寸为150 m×70 m×35 m。为了减小边界效应,设置边界约束条件为模型上顶面自由,下底面为固定面,其余4个面均限制其水平方向的位移,保证情况与实际工程相符。土体采用摩尔?库伦模型,支护结构采用弹性模型,结构参数如表2所示。 r 为隧道内径, R 为隧道外径, O 为隧道圆心。隧道开挖采用交叉中隔墙法,隧道埋深位置为10 m,其中,双隧道之间的净距为15 m,施工顺序采用先开挖左线隧道,开挖进尺达到15 m后进行右线隧道的开挖。
3 飞机荷载计算模型
选择目前世界上最大的载客飞机机型 A380-800作为此模型进行模拟研究,在起飞、降落及滑行阶段中,A380-800的飞机最大滑行重量为5620 kN,最大起飞重量为5600 kN,最大着陆重量为3860 kN,主起落架荷载分配系数 p 为0.97,起落架布置图如图3所示[17]。
将飞机荷载简化为节点动力荷载加载于隧道模型,研究飞机滑行通过隧道上方地表不同位置情况下飞机荷载对地表沉降的影响。将主起落架荷载分配系数 p 代入式(1)和式(2)中进行飞机前轮轮载和主起落架轮载的计算。
式中:F1为前轮轮载;F2为主起落架轮载;N1为前部机轮个数; N2為后部机轮个数; P1为飞机的最大滑行重量。
飞机机轮直径为1.5 m,当飞机滑行速度为55.6 m/s 时,机轮转动速度!= v/r =74:1 rad/s ,机轮转动频率f =!/2π=11:8 Hz。考虑到滑行过程中飞机存在振动效应,因此,模拟过程中将飞机荷载放大10%[18-19],得到前轮动荷载 F3和主起落架动荷载 F4。飞机前后轮动力荷载时程曲线如图4所示, t 为时间。
4 飞机荷载对单隧道工程地表沉降的影响
对于单隧道工程,由于飞机前后轮轮载的不同,当飞机滑行经过隧道上方地表时,飞机与隧道之间的相对位置关系变化会引起地表沉降变化。利用节点动力荷载法将飞机荷载作用在模型上,荷载均由模型左侧向右侧加载,荷载作用位置如图5所示,地表沉降曲线选取位置为飞机荷载作用节点位置处。
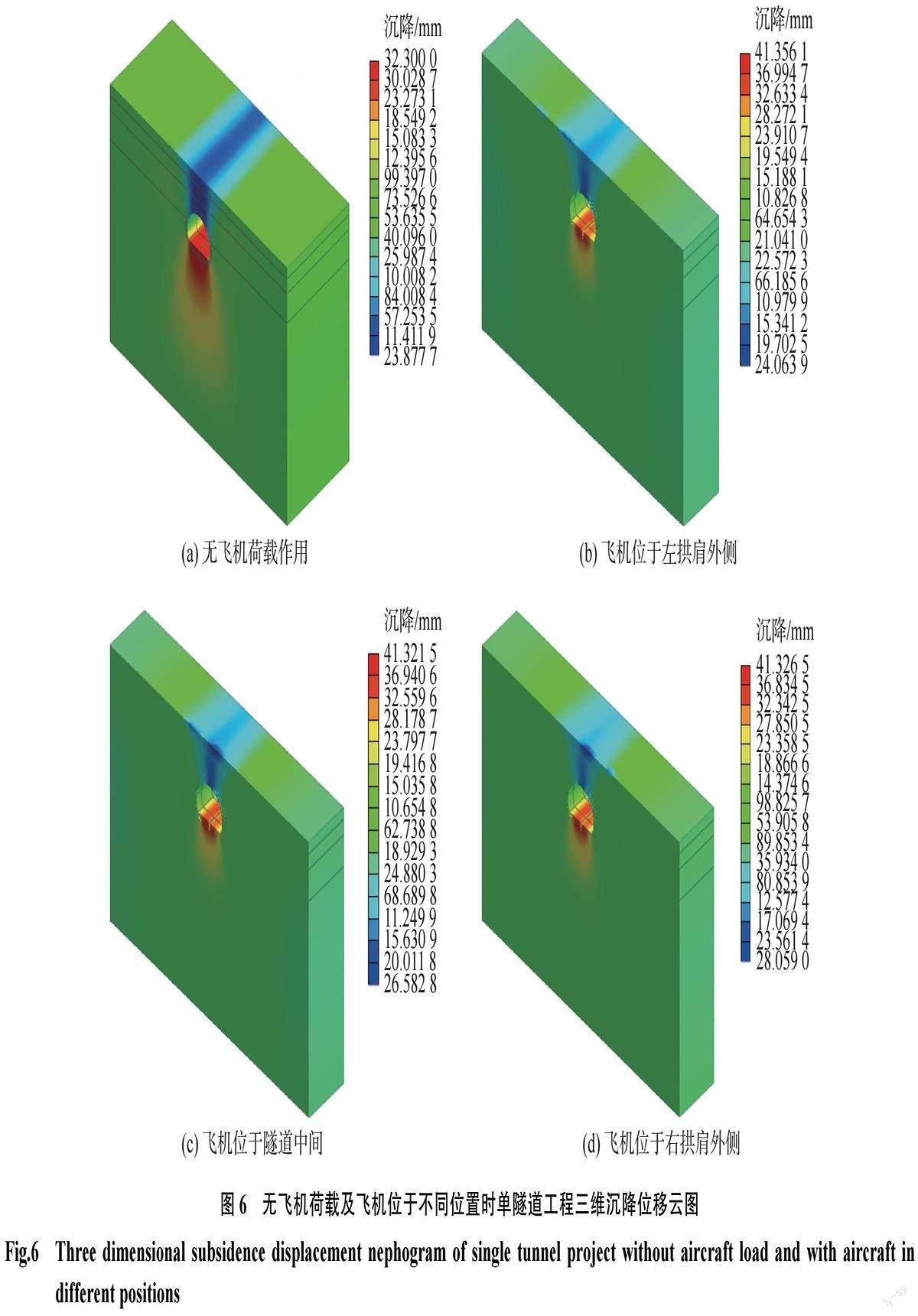
图6为无飞机荷载及飞机荷载位于隧道左拱肩外侧、隧道拱顶正上方、右拱肩外侧的三维沉降位移云图。当飞机位于隧道左拱肩外侧时,可以看出,飞机荷载的存在使得左侧作用位置附近沉降增大,但最大沉降点仍位于截面拱顶处,最大沉降值为24.1 mm,相比于无飞机荷载的情况,最大沉降量略有增大。飞机滑行至隧道拱顶正上方时,由于飞机荷载的作用,在其影响范围内的土体沉降增加,同时它的扰动作用影响了下部隧道施工,使得拱顶处的最大沉降增大为26.6 mm,相比无飞机荷载情况下增加了2.7 mm。飞机位于隧道右拱肩外侧时,截面拱顶处出现最大沉降约为28.1 mm,相比飞机位于隧道正上方时的最大沉降增大了1.5 mm,主要原因为此时飞机离开隧道拱顶上方时间较短,其对拱顶上方土体的扰动作用还未完全消失,同时飞机对隧道中线上部土体产生扰动作用与右侧土体扰动影响相互叠加。
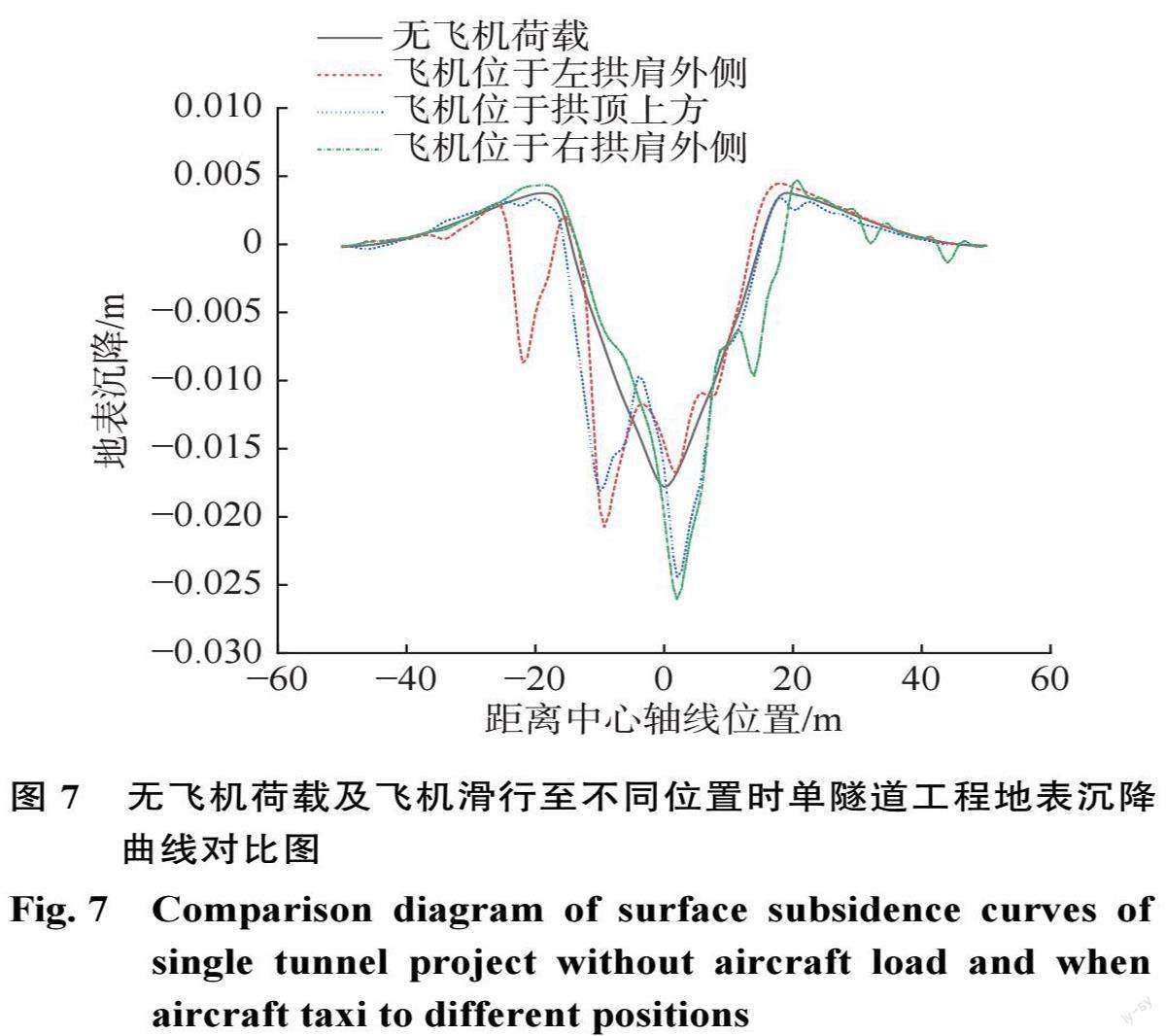
在隧道施工的过程中,飞机滑行经过隧道上方时,滑行经过的位置不同,对地表沉降的影响也不同。图7为无飞机荷载及飞机荷载位于隧道左拱肩外侧、隧道拱顶正上方、右拱肩外侧的沉降曲线。从图7中可以看出,飞机滑行经过隧道上方与无飞机荷载作用时的情况不同,地表沉降曲线不再呈 V 型,飞机荷载作用于不同区域大幅度改变了地表沉降曲线的形状,当飞机滑行至隧道拱顶正上方时沉降曲线近似呈 W 型。当飞机位于隧道左拱肩外侧时,左侧土体的沉降相对较大,右侧土体沉降曲线与无飞机荷载时相似;飞机逐渐向右滑行至隧道拱顶正上方时,地表沉降最大值所处位置由左拱肩向右过渡到隧道中线附近。飞机继续向右滑行至隧道右拱肩外侧时,右侧土体的沉降增大;但由于飞机刚离开隧道拱顶上方,对其沉降的影响还未完全恢复,因此,仍在隧道中线附近取得地表沉降最大值;此时左侧土体沉降有所恢复。当飞机由隧道左侧滑行至隧道右侧时,地表沉降最大值由19.4 mm逐渐增大到24.4,26.1 mm ,相对增加25.8%,34.5%,说明当飞机滑行经过隧道拱顶正上方并离开的较短时间内,地表沉降最大,此时对隧道施工安全和周边构筑物最为不利,因此,在施工过程中应尽量减少隧道施工与飞机滑行同时进行,且采取有效措施保证安全。
5 飞机荷载对双隧道工程地表沉降的影响
在双隧道工程中,飞机由隧道左侧滑行经过隧道右侧时,飞机荷载位于隧道上方不同位置对地表沉降的影响与单隧道工程有所不同。图8为双隧道工程上方施加飞机荷载后的数值模型简图。
图9为无飞机荷载和飞机位于左侧隧道左拱肩外侧、两隧道中间、右侧隧道右拱肩外侧的三维沉降位移云图。在4种情况下,最大沉降均位于左侧隧道拱顶位置,这一情况与无飞机荷载情况一致。在3种荷载作用情况下,当飞机滑行至左侧隧道左拱肩外侧时,土体沉降最小,数值为30.6 mm ;当飞机滑行至两隧道中间时,最大沉降为41.5 mm ,为4种情况下沉降最大值;而当飞机滑行至右侧隧道右拱肩外侧时沉降反而有所减小,最大沉降为38.5 mm,主要是因为两隧道之间有一定的距离,此时飞机已经离开左侧隧道上方一段时间,其对土体沉降的影响有所恢复。相比于无飞机荷载的最大沉降26.8 mm,有飞机荷载作用情况下最大沉降均增大,因此,在施工过程中应严格加强左侧隧道拱顶位置处的沉降监测。
图10为无飞机荷载及飞机滑行至不同位置时双隧道工程的地表沉降曲线对比图。由图10可知,飞机荷载的作用不改变地表沉降曲线的整体趋势,曲线仍近似呈 W 型,荷载作用下沉降比无 荷载时大。可以看出,当飞机的位置不同,沉降 曲线的形状也略有不同。当飞机位于左侧隧道左 拱肩外侧时,地表沉降最大值位于左侧隧道上 方,受飞机振动作用,左侧曲线发生起伏波动; 当飞机滑行至两隧道中间时,地表沉降曲线呈 W 型,主要是由于飞机对两侧土体的影响情况相 近,地表沉降最大值仍位于左侧隧道上方,且此 时两隧道中间地表的沉降量为 4 种情况的最大 值;飞机位于右侧隧道右拱肩外侧时,地表沉降 最大值位于右侧隧道上方,同时飞机的振动作用 使得右侧曲线发生起伏波动。对比荷载作用下的 3 种情况,当飞机由模型左侧滑行至右侧时,地表 沉降最大值先向左侧有所偏移后转移至右侧隧道 上方,最大值由无飞机荷载时的 27.2 mm 增大至 28.2,36.6 和 36.7 mm。
在单隧道、双隧道工程中,将无飞机荷载、 飞机位于单隧道拱顶上方和飞机位于两隧道中间 的 4 种情况进行对比分析,图 11 为地表沉降曲线 对比图,可以看出,双隧道工程的地表沉降变形 范围及沉降较单隧道工程更大。单隧道工程中沉 降曲线由无荷载情况下 V 型变成非对称式 W 型, 而双隧道工程中沉降曲线在无飞机荷载和有飞机 荷载作用下均近似呈 W 型。在单隧道工程中, 地表沉降最大值由 19.4 mm 逐渐增大至 24.4 mm, 增加了 25.8%;在双隧道工程中,地表沉降最大值 由无飞机荷载时的 27.2 mm 增大至 36.6 mm,增加 了 34.6%。由图 9~11 可以得出,在单隧道工程中,飞机位于隧道拱顶上方时沉降小,相对无飞 机荷载时沉降增加值也较小;双隧道工程中飞机 位于两隧道中间时,地表沉降相对无荷载时明显 增大。在无荷载情况下,双隧道工程地表沉降较 单隧道增大了 40.2%,因此,在施工过程中需全程 严格监测双隧道工程隧道拱顶处地表沉降。
6 结 论
以某机场隧道工程实例为背景,研究了飞机起飞对隧道施工过程中地表沉降的影响,通过三维有限元软件 MIDAS GTS NX 进行数值模拟,分析了飞机荷载对单线隧道和双线隧道地表沉降的影响规律。具体结论如下:
a.飞机滑行经过单隧道工程上方,飞机所在位置不同,地表沉降曲线形状不同。当飞机在单隧道两侧拱肩的外侧时,会对其所在位置地表沉降造成极值且附近地表沉降有所起伏;飞机由隧道左侧滑行至右侧时,地表沉降最大值由左侧移至中间偏右侧位置,且最大值不断增大。
b.飞机滑行经过双隧道工程上方时,地表沉降最大值由先行隧道上方逐渐转移至后行隧道上方,且在飞机所在位置附近造成地表沉降的起伏;当飞机荷载刚经过两隧道中间,位于后行隧道拱肩上方时,地表沉降最大且超过30 mm。在单隧道工程中,地表沉降最大值增加了25.8%;在双隧道工程中,地表沉降最大值增加了34.6%。因此,在飞机荷载作用下应严格监测双隧道工程地表沉降,在施工过程中应尽量与飞机在隧道上方滑行错峰。
c.本文建立的所有数值模型中,三维沉降中的最大沉降均位于拱顶位置处,向周围方向沉降值逐渐减小,因此,在施工过程中,除了应定时进行监测外,需重点关注拱顶处沉降情况。
参考文献:
[1]杨福麟, 刘永林, 胡斌.武汉地铁隧道开挖引起地表沉降的数值模拟研究[J].工程地质学报, 2013, 21(1):85–91.
[2] WEI G. Prediction of soil settlement caused by double-lineparallel shield tunnel construction[J]. Disaster Advances, 2013, 6(6):23–27.
[3]姜忻良, 赵志民, 李园.隧道开挖引起土层沉降槽曲线形 态的分析与计算[J].岩土力学, 2004, 25(10):1542–1544.
[4]孙玉永, 周顺华, 宫全美.软土地区盾构掘进引起的深层位移场分布规律[J].岩石力学与工程学报, 2009, 28(3):500–506.
[5]唐正, 王洪新, 孙德安, 等.大断面管幕法隧道群管顶进的地表位移规律研究[J].岩土力学 , 2022, 43(7):1933–1941.
[6]鲍先凯, 曹嘉星, 段东明, 等. Midas/GTS 在软岩隧道施工设计中的应用[J].公路, 2019, 64(7):321–325.
[7] DING Z D, JI X F, LIN X Q, et al. Numerical investigation of 3D deformations of existing buildings induced by tunnelling[J]. Geotechnical and Geological Engineering, 2019, 37(4):2611–2623.
[8]范雨, 苏艺, 袁勇, 等.复合地层双线地铁隧道施工地表沉降规律研究[J].地下空间与工程学报, 2020, 16(S2):762–768.
[9]郑爱元.小净距双线隧道施工衬砌稳定性分析[J].工程技術研究, 2019, 4(16):30–31.
[10]丁振义.双线隧道施工引起的地表沉降及其控制措施研究[D].西安:西安科技大学, 2019.
[11]牟天光, 祝江林.不同施工条件下双线盾构隧道施工引发地表变形规律研究[J].湖南文理学院学报(自然科学版), 2020, 32(4):75–79.
[12]桂登斌, 王玉锁, 何锁宋, 等.飞机动荷载下明挖隧道动力响应研究[J].现代隧道技术, 2019, 56(S2):320–324.
[13]魏晓刚, 杨柳川, 刘会丽, 等.机场跑道下穿隧道结构稳定性影响因素研究[J].工业建筑, 2022, 52(1):165–173.
[14]王志新, 王波, 李昊, 等.飞机荷载引起的层状地基附加应力及对下穿隧道的影响范围研究[J].土木工程学报, 2020, 53(S1):258–264.
[15]张召峰, 傅鹤林, 李成威, 等.移动飞机荷载对机场跑道下方土体的附加应力分析[J].现代隧道技术 , 2022, 59(S1):1111–1119.
[16]刘凯, 吴再新, 杨吉忠, 等.飞机降落冲击荷载作用下高铁隧道疲劳寿命及抗减振措施研究[J].隧道建设(中英文), 2022, 42(S1):281–288.
[17]姜昌山, 秦汉昌, 杨山, 等. MH/T 5004–2010, 民用机场水泥混凝土道面设计规范[S].北京:中国民航出版社 , 2010.
[18]高峰, 付钢, 胡文亮.移动飞机荷载对机场下部隧道的影响[J].重庆交通大学学报(自然科学版), 2012, 31(2):218–222.
[19]王力.飞机动载作用下复合式 TBM 下穿跑道设计方法及施工控制基准[D].成都:西南交通大学, 2018.
(编辑:石 瑛)
——结构相互作用的影响分析

