基于“5E”教学模式的概率论与数理统计课程教学管理初探

白雪婷 杨琴乐

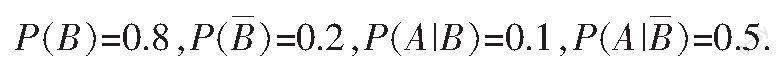
摘 要：本研究结合“5E”教学模式，在概率论与数理统计课程教学的过程中融入唯物辩证法的哲学思想。以学生为中心，通过加强课前管理、创新教学模式、提升教学水平、丰富教师素养，做到让学生课前自觉“收心”，课中主动“参与”，保证课堂教学活动的顺利进行，实现教与学的有效对接；利用“5E”教学模式中五个环环相扣的教学环节，采取积极正确发现问题、提出问题、分析问题、解决问题的思维方法，逐步引导学生敢于深入、善于融入，将现实生活、理论知识和品德修养联系起来，实现全员、全程、全方位育人。

关键词：“5E”教学模式；唯物辩证法；概率论与数理统计；教学管理

中国特色社会主义进入了新时代，教育的基础性、先导性、全局性特征和作用愈加凸显。从教育事业的全局来看，知识的传授与获取、教与学的关系正在发生变革，人们迫切需要更高质量、更加公平、更具个性的教育来满足社会需求。《中国教育现代化2035》提出要强化对学生实践动手能力、合作能力、创新能力的培养，高等教育工作者必须抓住机遇，不断创新教学模式，构建高效课堂。“5E”教学模式致力于提高学生学习兴趣，强调以学生为中心，通过吸引（Engagement）、探究（Exploration）、解释（Explanation）、迁移（Elaboration）、评价（Evaluation）进行高质量的教学设计，注重围绕学生的现实生活并逐步培养学生的科学探究能力。

概率论与数理统计是一门研究生产生活随机现象中隐藏的固有统计规律的课程，课程内容虽贴近生活但理论性、逻辑性强，教师在课堂上必须采取各种有效教學手段和方法，充分调动学生学习热情，使其能利用所学的知识和掌握的技巧去解决实际问题。如何提高概率论与数理统计的教学成效，成为大学数学课程教学改革的一大热点。为此，培养学生对随机现象的直观感受和理论上的严谨推理，掌握偶然与必然的统一思想，体会概率知识在生活中的广泛应用，养成批判性思维与辩证性思维，树立质疑、求真、求实、创新的科学态度，成为该课程的主要教学目标。借助“5E”教学模式将唯物辩证法的哲学思想融入概率论与数理统计课程教学，能够突出学生在教学过程中的主体地位，激发学生的创新思维，凸显知识的逻辑性与实用性，促进学生在认知领域和自我领域的发展，让他们在掌握知识的同时明确知识的应用方向。“5E”教学模式也为该课程实现思想政治教育与知识教育的有机统一，提供了一条有效的改革路径。

一、基于“5E”教学模式的课堂教学管理策略

课堂教学管理是指教师为了创设良好的教学环境，引导学生学习、减少不良行为，保证教学活动顺利进行而采取的一系列措施。管理好课堂是开展教学活动的基石，但是很多高校教师课堂管理经验不足，甚至有的教师只专注于“教”，完全忽略“管”，学生课堂“不抬头、不动手、不参与”现象频繁出现，教学质量不高。“5E”教学模式强调师生互动，注重学生的参与，将“5E”模式融入课堂可以帮助教师有效管控课堂，提升“教”与“学”的融合度。根据师生调研、师师调研、资料查阅，课题组给出几点改善课堂管理的策略。

（一）加强课前管理，让学生“收心”

大学数学课程内容较多，但是课时较少，学生课前预习不足，课后复习不充分，知识掌握不扎实。教师可以有效利用课前几分钟，利用“学习通”平台设置“问题式”签到，既可以让学生复习上节课所学知识，又可以将学生迅速拉回到课堂，准备新内容的学习。

（二）创新教学模式，让学生“参与”

不同学生学习能力和已有知识水平差异较大，这是教师在教学中普遍面临的问题。教师在教学中应当针对学生的多样性，采取灵活的教学方式（提问式、师生交流式、生生讨论式）授课，循序渐进，让吸收能力较差的学生有机会思考，让学习能力较强的学生有机会探索。

（三）提升教学水平，让学生“知用”

“数学无用论”是很多学生不愿意学数学的原因之一，优秀的数学教师不是会教数学，而是会用数学。大学校园活动丰富，学习资源充足，将有趣的、实用的、符合学生所学专业的实际案例融入教学，能够让学生对数学有新的认识，感受到数学有用，愿意走进数学课堂。

（四）丰富教师素养，让学生“愿学”

“口者，心之门户，智谋皆从之出。”教师在教学中应采用恰当的语言鼓励学生，为学生营造良好的学习氛围。这有助于学生获得存在感和安全感，能够拉近师生之间的距离，让学生主动打开思维，想思考，想学习。

二、基于“5E”教学模式的课程教学设计思路

著名心理学家洛钦斯通过实验证实了首因效应（也称“第一印象”）的存在，实验表明人与人在第一次交往中给彼此留下的印象，能够在对方的心中留下很深的烙印。吸引（Engagement）作为“5E”教学模式的开始环节，符合人类心理活动的需求。因此，课程内容的引入要具备强大的感染力。教师在课前应充分了解学生已有的背景知识，尽量选取与学生生活贴近的问题吸引学生，把握好每节课刚开始的5分钟。课题组结合“5E”教学模式和唯物辩证法的哲学思想，给出概率论与数理统计中著名的贝叶斯公式的教学设计。

（一）创设问题情境——吸引（Engagement）

教师行为：播放影片《狼来了》，带领学生重温耳熟能详的寓言故事，让学生再次体会小男孩的行为和羊群葬身狼腹的原因。然后，引导学生分析三次喊狼来了的过程中小男孩的可信度是如何下降的。根据已有知识，假设“小男孩说谎”记作事件A，“小男孩可信”记作事件B。村民听到“狼来了”的喊声，毫不犹豫冲上山打狼，最终发现狼没来，结果表明小男孩第一次说了谎。于是村民根据小男孩的失信行为对小男孩的可信度发生了改变，请大家思考怎样衡量小男孩在第一次说谎后的可信度。

初始环节以一则小故事引入，告诫学生诚信的重要性，使其明白“量变会导致质变”的唯物辩证法思想，懂得“事不过三”的哲学道理。激发学生的学习兴趣，引导学生进行深入思考，为探究环节奠定良好基础。

（二）激发认知冲突——探究（Exploration）

授课教师根据第一环节提出的疑问，进一步引导学生尝试利用合作式探究学习形式再次深入思考。整个过程中，教师要注意观察倾听，了解学生探究的进程和深度，避免学生急于求成，过快得出不严谨的结论。

学生行为：小男孩第一次说谎后可信度变为P（B|A），本质上是一个条件概率，根据条件概率公式有P（B|A）=，分子利用乘法公式知P（AB）=P（B）P（A|B），而分母中事件A的概率（即小男孩说了谎）可通过所学全概率公式计算得到（设为B“小孩不可信”），有P（A）=P（B）P（A|B）+P（B）P（A|B）。

在探究环节中，学生进行了推理思考，观点得到不断丰富，思维逐渐清晰，为之后顺利得出定义创造了条件。与此同时，学生也真切感受到事物是普遍联系的，不积小流无以成江海，不积跬步无以至千里。

（三）主导推理演绎——解释（Explanation）

“5E”教学模式的关键环节在于解释（Explanation），该环节可以帮助学生将探究活动中收集到的知识信息进行合理规范的解释，让学生尽可能根据自己的理解描述概念、性质、定理等内容，促使学生深刻理解知识的形成过程，做到“事要知其所以然”。

教师行为：跟学生一起分享数学家贝叶斯的故事，解释贝叶斯公式的来源，给出贝叶斯公式的科学表达式，并用真实数据解释男孩可信度下降的原因。

设Ω为样本空间，A为Ω中的事件，B1，B2，…Bn为Ω的一个划分，P（Bi）>0，i=1，2，…，n，且对任意事件A，P（A）>0，则：

《狼来了》寓言故事中，假设村民一开始对小男孩的可信度为：

根据贝叶斯公式计算得：

这表明，村民经历小男孩第一次说谎后，对小男孩的可信度调整为：

再次利用贝叶斯公式得：

以上数据说明，村民经历上当后，对小男孩的可信度从最初的0.8下降到0.138，如此低的可信度，揭示了村民在第三次听到“狼来了”的喊声后无动于衷行为背后隐藏的客观规律，再次警示我们要懂得“质量互变”的规律，使学生领悟到“勤学如春起之苗，不见其增，日有所长；辍学似磨刀之石，不见其损，日有所亏”的深刻含义。

（四）指引实践应用——迁移（Elaboration）

迁移环节旨在引导学生将新知识用在新场景或者相类似的场景中，进一步促进学生对理论内容的消化吸收和应用。教师可以通过实践练习，鼓励并引导学生尽量使用专业术语，让他们对刚学的概念进一步加深理解，通过拓展练习获得更多技能。

教师行为：贝叶斯公式是在“结果”已发生的条件下，计算这一结果是由“原因”造成的可能性，是“执果索因”的问题，即后验概率，进而引导学生区分条件概率、先验概率和后验概率。例如，某肿瘤医院收集了该院一年内乳腺肿块病例，临床表现见表1。现有一患者肿块表面不整齐，医生该如何诊断？请分析计算结果并总结先验概率和后验概率在医学诊断中的临床指导意义。

根据表中数据得：

再利用贝叶斯公式计算可得表2。

由以上医学案例可知，先验概率和后验概率截然不同，如若混淆容易造成误诊。由表2可知，先验概率可以提高诊断效果，但是准确性不高。后验概率对原有事件发生的可能性进行修正，进一步提高诊断的准确性。这个案例告诫我们，事物间的因果關系具有复杂性和多样性特点，“一因多果”与“一果多因”情况时有发生，面对不好的结果不要恐慌，而要找到真正的原因并科学地解决。

（5）鼓励反思评估——评价（Evaluation）

评价是“5E”课堂教学的最后环节，主要采取教师评价、小组互评、学生自评等多种评价方式相结合的混合评价模式，为教师提供了一个评估教学过程和教学效果优劣的机制，也有助于学生总结获取知识的思路、方法和技能。以贝叶斯公式教学为例，教师应在教学中注重分层教学，根据学生的发展差异设计教学内容，让学生实现思维与行动上的跨越，形成活泼、互帮、互赶的学习氛围；学生在学习中要有意识地培养自己严谨的推理思维、科学的探索精神和准确的计算能力。

三、总结

概率论与数理统计课程研究随机现象及其规律，其中蕴含大量的哲学思想。课题组以贝叶斯公式为例，探讨了如何将唯物辩证的哲学思想融入“5E”教学模式，进而有效开展概率论与数理统计课程教学工作，并在“三全育人”理念下实现数学课程知识传授与价值引领相结合的教学目标。为进一步改善概率论与数理统计的教学效果，高校教师要不断提升教学水平，探索更高效的教学方法与教育模式，着力将教书育人落实于课堂教学的主渠道之中，引导学生进一步认清自身在教学过程中的“中心”地位，增强学生的创新意识和创新能力，从而培养出更多更适合现代社会发展需要的应用型与创新型人才。

参考文献：

[1]吴成军，张敏.美国生物学“5E”教学模式的内涵、实例及其本质特征[J].课程教材教法，2010（6）.

[2]张丽静，赵鲁涛，李娜.基于唯物辩证法的概率理论与数理统计课程思政建设与实践[J].大学数学，2022（2）.

[3]臧鸿雁，刘林，张志刚.概率论与数理统计教学案例研究[J].大学数学，2022（2）.

[4]田苗，陈俊英，王福顺.概率论与数理统计课程“四合三联”创新性教学体系探索[J].中国大学教学，2022（8）.