规则压缩模型和灵活架构的Transformer加速器设计

姜小波 邓晗珂 莫志杰 黎红源

①(华南理工大学电子与信息学院 广州 510000)

②(广东科学技术职业学院机器人学院 珠海 519090)

1 引言

自然语言处理(Natural Language Processing,NLP)技术在人工智能(Artificial Intelligence, AI)领域具有重要地位和作用，赋予机器从不同结构的文本中获取和处理知识与信息的能力，并且能够与人进行交互，被广泛应用于机器翻译、情感分析和聊天机器人等场景。随着深度学习的发展，各种用于NLP的模型层出不穷，近期基于自注意力机制的Transformer[1]模型及其变体在各种NLP任务上显示了优越的性能[2-6]，远超传统的基于卷积神经网络(Convolutional Neural Network, CNN)[7]和递归神经网络(Recurrent Neural Network, RNN)[8]的模型。但硬件的发展远远落后于模型的发展，限制了Transformer自然语言处理模型的发展和应用。

Transformer卓越的性能是由复杂的模型带来的。模型的复杂包括数量上的复杂和结构上的复杂。数量上的复杂性包括模型参数量与运算量的爆炸增长。参数和计算复杂度的指数级增长给Transformer的硬件设计带来了巨大的挑战。对硬件设计更大的挑战是模型结构上的复杂性，表现为参数和计算分布上的不规则性。这种不规则性带来了模型和硬件的不匹配，包括模型复杂运算和规则运算阵列的不匹配；模型分布式参数和硬件集中式存储器的不匹配；复杂模型运算过程的参数不均衡性和硬件固定的不匹配。这些不匹配降低了Transformer模型映射到加速器的性能和效率。当前研究更多地集中在解决模型数量上的复杂性，对结构上的复杂性，研究得比较少。

Transformer模型具有数量上的复杂性，包含海量的参数和运算，而且具有很大的冗余性。现有研究通过模型压缩减少模型规模。Voita等人[9]使用头部剪枝，计算每个注意头的重要性分数，然后修剪分数较低的注意力头。Lin等人[10]将模型中的残差模块惩罚到同一映射，通过阈值算子来识别和丢弃残差连接中不重要的非线性映射。Peng等人[11]提出了一种列平衡块权重修剪算法，在每个权重矩阵的列中进行分块剪枝。这些研究有效地减少了参数和运算量。但对于模型结构方面的复杂性，研究得比较少。而这恰恰是Transformer模型加速器设计的关键。

由于模型中不同权重矩阵的稀疏性和计算模式不一致导致映射到规则的运算架构和集中式存储架构时效率不高。如Peng等人[11]和Qi等人[12]使用的稀疏模型，其各行列非零元素的随机性及剪枝率不同导致的计算量不一样，映射到同一运算阵列造成的处理单元(Processing Unit, PE)停顿降低了PE利用率。Li等人[13]使用的异构运算阵列由于其运算单元的多样化、固定的硬件资源分配及复杂性更高的傅里叶变换运算，PE利用率不高且增加了PE单位运算功耗和额外的控制开销。Zhang等人[14]使用乘加分离的运算架构映射外积数据流，可以减少中间结果存储但是乘加运算量不一致导致运算阵列停顿。Park等人[15]使用的不规则稀疏导致负载不均衡，并且复杂的索引匹配导致过多的存储开销和功耗。存储架构的设计同样影响着芯片的性能，文献[11-14]的运算阵列与片上总缓存模块直接交互，中间结果的移动距离较大导致单位数据移动功耗增加，集中式的片上缓存管理由于运算阵列与存储单元的远距离交互使得数据的单位读写功耗相对较高。目前的加速器架构一般采用集中式的存储架构，而人脑中的神经元采用完全分布式的参数存储模式，获得了很高的运算效率和能效。

本文通过降低模型结构上的复杂度，提高硬件的灵活性，从而降低模型和硬件上的失配，提高模型到硬件上的映射效率。本文提出一种规则的模型压缩方法，采用规则的偏移对角矩阵的权重剪枝方案。同时提出一种灵活的脉动运算阵列，在获得更高的数据复用率的同时减少普通脉动阵列具有的阵列间数据移动开销。本运算阵列对提出的偏移对角矩阵能进行高效的映射，极大减少索引开销的同时平衡了计算负载和提高了数据复用率。本文受人脑神经元完全分布式存储参数启发，提出一种准分布的存储架构，提高存储效率的同时大幅度降低了权重数据搬运。

2 模型压缩

本文在Transformer模型压缩领域首次提出基于偏移对角矩阵的权重剪枝方案，得到的权重从整体到局部都具有规则化特点，在高压缩率的同时保持硬件实现时运算阵列层面的整体规则性以及运算单元的局部规则性高效映射，同时便于准分布存储架构的数据存取，可以实现高资源利用和低索引开销的高效部署。剪枝后的模型采用硬件友好的量化方法，简化硬件量化推理逻辑，在硬件中通过移位操作代替浮点乘法。为了减少精度损失，提出一种针对Transformer模型量化系数联合调整方法。模型压缩包括剪枝和量化两个步骤。

2.1 剪枝

偏移对角矩阵是一种非零值分布在对角线或者是偏移后的对角线上的结构化规则稀疏矩阵，如图1所示。根据Deng等人[16]在CNN模型中的研究中得到了偏移对角矩阵神经网络的存在性，并且证明了偏移对角矩阵神经网络具有和普通神经网络一样的通用逼近性质，从理论上说明了使用偏移对角矩阵进行模型剪枝的可行性。基于以上工作，本文将模型中的权重矩阵分为多个子矩阵并基于偏移对角矩阵进行结构化剪枝，可以得到整体和局部非零值规则分布的稀疏矩阵。鉴于Transformer模型参数的复杂性，为达成结构化剪枝的目的和减少模型精度损失，本文的方法尽可能维持了原权重参数分布特点，对训练好的模型中的参数使用偏移对角矩阵进行剪枝，如图2所示。

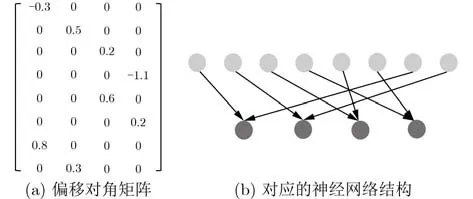
图1 偏移对角矩阵

图2 偏移对角剪枝

将总体的权重数据分为4类，包括：多头注意力输入线性层权重(Q,K,V)、多头注意力输出线性层权重(O)、前馈神经网络第1层线性层权重(FFN1)和第2层线性层权重(FFN2)。随后对分类的权重进行剪枝，遵循“训练-剪枝-再训练”和分批剪枝相结合的策略。在剪枝训练过程中，每次分批剪枝只剪枝一类权重，并且每批权重剪枝后获取下批权重的剪枝偏移量，这种策略可以更好地获取最佳的偏移，避免一次性剪枝大量参数所带来的性能大幅下降。剪枝流程如算法1所示，算法输入为剪枝前的模型，输出为剪枝后的模型，伪代码第3行对模型进行训练，第4行使用GetOffset算法获取Q,K,V权重矩阵的偏移量，第5行使用Prune算法对Q,K,V权重矩阵进行剪枝，以此类推后续代码中按顺序依次获取模型中权重矩阵O, FFN1, FFN2的偏移量，完成模型的偏移对角结构化稀疏剪枝。再训练的目的是减少精度损失，使模型进行自适应微调。

算法1 单位偏移对角剪枝

在剪枝步骤中，GetOffset根据权重的数据分布特点和偏移对角矩阵的子矩阵大小获取用于剪枝的偏移量，将权重矩阵分为多个子矩阵，每一个子矩阵单独计算偏移量，如式(1)所示，其中p为偏移量，xi,j为子矩阵中的元素。Prune根据偏移量以及子矩阵大小将分布在非偏移后的对角线的权重进行屏蔽，将值设置为0且在训练过程中不进行参数更新。为了避免剪枝后的多头注意力层内部相似度计算差异度不明显，导致注意力性能下降，本文在剪枝多注意力层的训练微调过程中取消多头注意力计算的缩放操作，以此扩大注意力计算结果的差异性，在实验中发现这样得到更高的BLEU分数。

2.2 量化

由于训练后的模型参数数据分布大致以0对称，本文使用了均匀对称量化对训练后的模型进行了8 bit量化。为了减少量化和去量化操作带来的额外的硬件资源和硬件功耗，本文将这些量化系数简化为2-n的形式，在硬件中通过移位操作代替浮点乘法。为了减少精度损失，提出一种针对Transformer模型量化系数联合调整方法。以注意力层为例，注意力层的第1部分包含查询向量的线性层计算、键向量的线性层计算和两个线性层结果的点积计算。为了保持softmax函数的输入数据的原始度，通过对线性层的参数进行联合调整

其中，q表示查询向量，k表示键向量，Q和K分别表示查询向量线性层的输出和键向量线性层的输出，Wq和Wk分别表示查询向量线性层和键向量线性层的权重，bq和bk分别表示查询向量线性层和键向量线性层的偏置。γ表示缩放系数，γ的值取决于量化带来的量化误差最小。

为了计算层归一化，在推理过程中需要计算输入样本数据的均值和标准差。在非通用计算平台的实现这些计算是复杂的，可能会成为硬件实现的延迟瓶颈。Wu等人[17]提出使用更加简化的L1范数来代替批量归一化中L2范数，本文将其运用到Transformer模型中的层归一化计算，实验证明不会对模型性能产生影响，如式(5)所示

其中，µd对应输入所在词向量维度的均值，CL1是一个归一化常数，取值√(π/2)，xi是输入所在词向量，n在这里表示词向量的维度，α和β是与L2范数的层归一化相同的可训练参数。可以看出，L1范数消除了平方和运算和开平方运算，降低了计算复杂度。

3 硬件架构设计

3.1 加速器整体架构设计模型

本文通过模型压缩大大减少了模型的储存消耗，但是压缩后的模型无法直接全部存储在片上缓存中，所以需要与片外动态随机存储器 (Dynamic RAM, DRAM)进行数据交互。如图3所示，总体硬件架构包括控制模块、片上缓存、运算阵列和非线性计算模块。片上缓存包括了输入缓存、权重缓存和中间结果/输出缓存，片上缓存采用乒乓操作用于支持数据的连续处理。加速器的整体数据流如图4所示，一个注意力子层或一层前馈神经网络的权重数据为单批读取权重大小，在计算过程中同步加载下一批权重数据。通过网络层顺序加载权重数据，并且将层间计算结果存储在片上用于下一子层计算，这样可以减少与片外DRAM交互次数。本文对注意力层的计算顺序进行了优化，让Softmax函数计算与矩阵乘加计算同步进行，可以减少计算等待时间。通过这种任务级调度，整个系统更高效地加速Transformer模型中的所有网络层计算。

图3 所提出的加速器总体硬件架构

图4 加速器整体数据流

3.2 准分布式存储架构

为了减少运算单元与存储单元的数据传输成本，包括了长距离传输导致的功耗和复杂的地址生成读写成本，本文使用了准分布式存储架构。在人脑神经元中，每个神经元都可以对电信号进行处理和存储，并将处理结果传递给与之相连的神经元，每个神经元分别对数据进行存和算，神经元之间以分布式方式相连，通过这种分布式互联完成神经元间的数据交互，是完全分布式架构。本文参考人脑神经元的分布式结构，以PE和本地寄存器(RF)模拟每个神经元的存储和计算，PE之间以分布式进行连接模拟神经元之间的分布式连接，PE阵列外使用FIFO, BRAM, DRAM等多级存储降低数据传输开销，总体架构为准分布式存储架构。

如图5所示，整个存储架构包括了PE本地寄存器、运算阵列内部缓存(FIFO)、片上全局缓存(BRAM)和片外DRAM等具有不同访问代价的多级存储层次。访问代价最低的PE内部的RF作为一个基本单元点，数据可以在各个基本单元点之间进行横向以及纵向的传递，从而将计算过程中数据固有的移动次数最大比例地放在访问开销最小的RF存储层级，最大限度消耗由上级存储写入的数据，降低移动功耗。从BRAM中读入运算数据时，将整个运算阵列看作一个整体进行数据输入，运算阵列内的基本单元点以分布式方式进行数据交互，输入数据在基本单元点中进行点与点之间的传递，实现输入、权重以及输出3个维度的数据复用。整个存储架构以准分布式的方式进行数据交互。

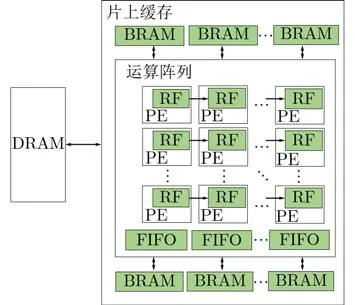
图5 准分布式存储架构示意图

相对于运算阵列来说，本地缓存可以存储矩阵计算的部分和结果，相比于将其存储在全局缓存，加法单元可以更快和更近获取部分和结果。另外，在计算非线性函数时，这种准分布存储架构还可以避免中间结果数据的重复读取以及减少重复计算，有利于加快推理速度。

3.3 运算阵列设计

如图3，运算阵列由PE和加法单元组成，每列PE共用一个加法单元。PE用于处理矩阵乘法，加法单元用于处理PE的结果相加以及部分和累加，可以根据实际推理需求进行拓展。剪枝后的偏移对角矩阵在整体上的规则性，即子矩阵的大小与排列都是规则的，可以100%高效映射到规则的运算阵列中。运算阵列内部采用权重固定的数据流方案，如图6所示，输入和权重分别以行形式和稀疏块形式送入运算单元，这样能够减少由于不同输入句子长度以及编解码器不同计算模式带来的运算阵列计算效率低下的问题。输入数据每个周期向右传输，实现输入复用，而数据规模最大的权重数据只需从运算阵列外读取1次。输出每个周期在加法单元内部进行逐周期累加，实现输出复用。

图6 运算单元数据流动方案

3.4 计算单元设计

计算单元包括PE和加法单元，每个PE包括乘法单元和RF存储单元，作为规则的分布式基本点，可以100%高效映射偏移对角矩阵的局部性，即单个子矩阵的行列维度以及非零值的规则分布。每个PE中包括16个乘法器和1个数据分配器，如图7所示，数据分配器的作用是根据偏移量对输入数据进行重新排列，保证输入数据和所对应的非零值权重数据相乘。无需在PE外进行稀疏解码，同时不用对部分和输出或计算结果进行地址索引，如图8所示。加法单元负责将所在列PE产生的部分和结果或者偏置数据进行加法运算，如图9所示，每个加法单元内部配备用于缓存部分和结果的本地缓存，缩短了部分和的数据移动距离，dense_en信号通过控制加法单元的数据源进行密集和稀疏数据通路的切换，加法单元支持激活函数ReLU。

图7 PE内部结构

图8 运算单元内数据

图9 加法单元

3.5 高效权重数据存储格式

为了进一步减少存储成本，本文对硬件中的权重数据存储格式进行了优化。根据前文分析，运算阵列采取权重固定的数据复用模式，所以将偏移量索引与权重数据进行同步存取，可以减少偏移量索引的读取次数。如图10所示，对偏移对角权重矩阵进行向上压缩，保留了非零数据的列索引信息，根据偏移量可以得到行索引。另外，每个子矩阵块共用1个偏移量，可以大幅降低索引成本。这种强规则性的存储格式在准分布式存储架构上实现了存储资源的最大化利用，避免了数据存储长度的不同映射到规则的存储单元中带来存储资源浪费的问题。表1对比了现有稀疏矩阵存储格式的存储代价，其中稀疏矩阵大小为[800,800]，稀疏度为50%。可以看出，本文的稀疏权重数据存储代价最低，具有最高的存储效率。因为每个偏移对角子矩阵中每列只有一个非零数据，这样保证了硬件加速器中的运算单元处理相同数量的非零数据，避免了稀疏剪枝可能带来的运算单元负载不均衡问题。

表1 稀疏矩阵格式存储代价对比

图10 偏移对角矩阵稀疏权重存储方案

4 实验与讨论

4.1 模型压缩实验

4.1.1 模型压缩实验结果

在本节实验中，使用的数据集为IWSLT-2014英语(En)-德语(De)互译数据集，以BLEU分数作为性能指标。BLEU是一种用于自动评估机器翻译结果质量的指标，通过比较机器翻译结果与参考答案之间的相似度来度量翻译质量，是机器翻译领域最常用的评估指标之一。Transformer模型的参数设置见表2，剪枝实验基于前文中提出的偏移对角矩阵剪枝方法，对Transformer模型中的权重数据分类后进行分批剪枝。

表2 Transformer参数设置

子矩阵大小的倒数为压缩后的参数量与压缩前的参数量之比，如子矩阵为4时压缩后的参数量为压缩前的1/4，此时压缩率为75%。在实际应用中，模型压缩率通常在50%以上且尽可能大，才能保证模型的轻量化以便降低实际应用中的推理功耗和延迟，但模型压缩率增大的同时其推理性能也在下降，需要找到一个最佳的平衡，本文从实际应用角度以及易于硬件实现的角度出发，使用大小分别为4和8的子矩阵进行剪枝实验，即压缩率分别为75%和87.5%，子矩阵大小为2的指数便于硬件设计的规则化实现，实验结果如表3-表5所示。首先对Transformer进行训练获取了基准模型以及BLEU分数(En-De为28.5，De-En为34.5)。在IWSLT-2014数据集的德英翻译任务中，子矩阵大小为4时，结合硬件友好的量化推理方法，将原始模型参数的32 bit浮点表示量化为8 bit整型表示，即在剪枝完成了75%的模型压缩基础上将模型再量化压缩75%，最终的参数量压缩率可以达到93.75%，精度损失小于1%，如表5所示。精度损失会造成翻译质量的下降，如语法语义等表达变差，BLEU分数表征的是翻译结果与参考答案的相似度，精度损失多少对翻译任务来说是可接受的并没有一个具体数值定义，但原始Transformer模型的BELU分数较优，翻译质量好，压缩后的模型相比原模型损失1%以内的精度可以认为是对翻译质量没有影响。

表3 Transformer模型(base)实验结果

表4 Transformer模型剪枝实验结果

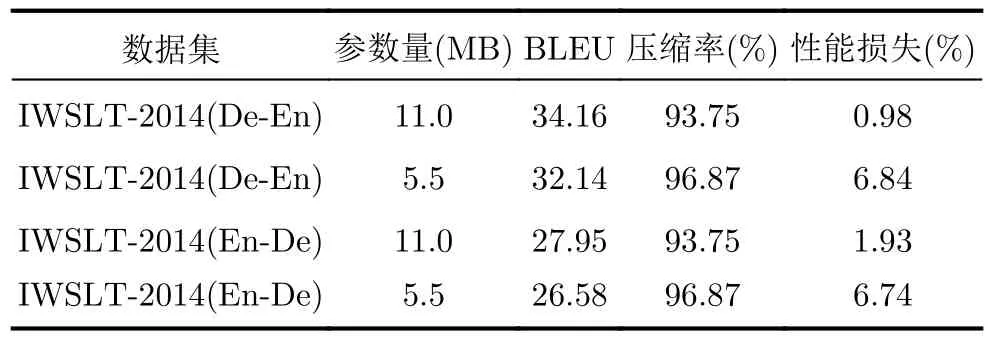
表5 剪枝后的Transformer模型量化实验结果

4.1.2 分批剪枝讨论

IWSLT-2014的En-De和De-En翻译任务的分批剪枝过程如图11所示。对于该任务，采取算法1中的分批剪枝方案，可以发现注意力层的剪枝后的精度下降小于前馈神经网络，说明在块大小较小情况下采用偏移对角权重矩阵不会对注意力层的性能造成较大影响。而采用块大小为8的子矩阵会导致每类权重剪枝后的精度损失更明显，尤其是前馈神经网络的第2层线性层。

图11 分批剪枝过程的精度下降趋势

4.1.3 与现有工作对比分析

本文的模型压缩方法与现有研究工作的性能对比如表6所示，可以看出，在相同任务和数据集条件下，本文的压缩率远比文献[24]高；与文献[13,14,23]对比，在模型压缩率相近的情况下本文的压缩方法性能损失较小。

表6 算法结果对比(%)

4.2 加速器性能评估

4.2.1 加速器硬件资源消耗

本实验的加速器设置输入最大长度为64，执行批量大小为1的推理，在ZC706开发版上评估所提出的加速器。时钟频率为200 MHz，功率为14.0 W，资源利用率报告如表7所示。

表7 资源利用报告

4.2.2 加速器单层推理效率

由于进行翻译任务时，模型的翻译性能以及实际翻译的目标语言的内容影响翻译句子长度，这会改变解码器的迭代时间。为了对比加速器的加速效果，对模型中编码器和解码器的子层计算延迟进行对比，如表8所示。其中，GPU为NVIDIA V100，MHA-RL包括多头注意层、残差连接和层归一化，FFN-RL包括前馈神经网络层、残差连接和层归一化。与GPU相比，本方案在计算MHA-RL和FFNRL时可以实现13.5倍和4.2倍的加速。与文献[26]相比，本文实现的加速器在计算MHA-RL时的加速比例有所降低，但是在计算FFN-RL时的推理速度是文献的1.24。另外，文献[26]的运算阵列使用了4 096个乘法器，而本文仅使用了1 024个乘法器，所以本文的加速器具有更高的硬件资源效率。

表8 与其他计算平台计算时间对比

4.2.3 加速器总体硬件性能对比

本文提出的Transformer加速器与现有研究工作的硬件性能对比如表9所示。其中传统平台性能对比中 CPU为Intel i7-8700K, GPU为NVIDIA 1080Ti，在计算过程中执行单批量推理，权重参数压缩率为75%，计算性能为单批量执行句子长度为64的德英翻译所得。与CPU相比，本文在FPGA实现的硬件加速器在计算性能、功耗和能效方面均有优势，其中能效比为CPU的12.45倍。与GPU相比，计算性能略低于GPU，但是在功耗和能效方面都有优势，其中能效比为GPU的4.17倍。

表9 加速器总体硬件性能对比

在与现有工作对比中，使用本文的加速器在75%压缩率下处理了标准Transformer模型的推理，实现了8.4 ms的推理延迟，具体性能见表9。表中列出了现有先进工作中FPGA加速器的性能，其中文献[26]采用的模型是6层编码器，文献[13]采用的模型是1层编码器和1层解码器，文献[14,25,23]采用的模型是标准Transformer(6层编码器和6层解码器)。通过吞吐量与功耗之比计算FPGA的功耗效率来进行性能对比，以CPU的推理能效作为基准，由表9可以看出，本文的加速器表现出了较好的效率。如果文献[13]采用标准Transformer进行推理，其等效能量效率为7.43，低于本文的12.5。因此，本文加速器的功耗效率明显高于现有研究工作。

5 结论

针对Transformer模型在数量和结构上的复杂性带来的加速器设计的困难，本文研究提高模型和规则硬件匹配度，提高模型和硬件的映射效率的方法。本文研究规则模型压缩和灵活硬件架构，设计了高性能低功耗的Transformer加速器。本文提出的规则的模型压缩算法，采用偏移矩阵剪枝算法和简化硬件量化推理逻辑的全局量化方法，可以在精度损失小于1%的情况下将模型压缩93.75%，并具有良好的规则性。本文提出了一个灵活的硬件架构，包括一种以块为单元的权重固定的脉动运算阵列，同时参考人脑神经元结构提出一种准分布的存储架构。获得了100%的算法映射效率，提高了参数存储效率，大幅度降低了数据移动功耗。在FPGA上实现的加速器，相比于CPU和GPU能效分别提高了12.45倍和4.17倍。