智能反射面辅助的抗干扰安全通信系统鲁棒资源分配算法

席 兵 冯彦博 邓炳光 张治中

①(重庆邮电大学通信与信息工程学院 重庆 400065)

②(南京信息工程大学电子与信息工程学院 南京 210044)

1 引言

无线信道的广播性为窃听者(Eavesdropper,Eve)提供了窃听和干扰的机会[1]，从而威胁到合法用户的通信安全。为了应对上述问题，许多新颖的无线传输技术被提出，其中波束成形，人工噪声(Artificial Noise, AN)和智能反射面(Intelligent Reflecting Surface, IRS)在物理层安全方面得到广泛探索和应用。其中，波束成形技术是将能量集中到很小的区域，并获得较高的增益，可以解决自由空间传播损耗较大的问题。AN辅助波束成形是发射信号时加入噪声，以略微牺牲用户接收信号质量情况下，大幅降低窃听者处的信干噪比，以此提升系统安全性[2]。IRS是一种应用于软件控制反射重构无线传播环境的高效节能技术。具体来说，IRS由嵌入在超表面的大量低成本反射元件组成，每个元件能够独立地改变入射信号的相位或(和)幅度，从而实现被动反射波束成形[3]。

在物理层安全增强方面，IRS辅助安全通信受到了学术界的广泛关注。文献[4]提出了一种IRS辅助的安全节能传输算法，在合法用户和Eve的信噪比限制下，最大限度地降低发射功率。同样，利用AN可以有效加强系统安全性，因此文献[5]提出了一种结合半定松弛法和丁克尔巴赫法的交替优化算法，通过联合优化IRS相移、波束形成向量和AN协方差矩阵，来降低用户的安全能耗。上述工作均是建立在完美信道状态信息(Channel State Information, CSI)为前提上，针对不完美CSI的问题，文献[6]分别考虑了有界CSI误差模型和统计CSI误差模型，在最小速率、速率中断概率约束下，构建了发射功率最小化问题。进一步考虑Eve对系统的影响，文献[7]研究了不完美CSI条件下，在Eve的最大可容忍数据速率和合法用户的最小速率要求约束下，提出了一种优化发射功率算法。为了提高系统的安全速率，文献[8]以最大化系统和安全速率为目标，在窃听信道不完美CSI条件下，提出了一种联合优化波束成形、IRS相移和AN协方差矩阵的交替优化算法。然而，该研究中限制了对直接信道的考虑，未充分考虑恶意干扰对系统性能的影响，也没有考虑最小用户服务质量的要求。针对上述工作并没有考虑恶意干扰对系统的影响，为此文献[9]研究了一种无人机通信系统，其中部署了IRS，以协助BS在干扰器存在的情况下传输信息到无人机，通过联合优化地面节点的发射功率、IRS的相移矩阵和无人机的飞行轨迹，最大限度地提高无人机通信的平均速率。然而文献[9]仅考虑功率分配，忽略了波束成形、窃听、不完美CSI和使用AN等因素的影响。与没有优化基站(Base Station,BS)波束成形向量的文献[9]不同，文献[10]在CSI不完善、干扰器波束成形向量不知情的情况下，通过联合设计BS的波束成形向量和IRS的相移，最大限度地提高系统的可达率。然而，文献[10]并未使用AN技术对抗窃听者的窃听，也未充分分析不完美CSI对系统性能的影响，并且仅考虑了单用户单窃听的简单通信场景。

上述工作大部分是建立在已知完美CSI或单用户单窃听的简单情况下，但是实际通信系统更加复杂，CSI难以准确获取[11]。为此，本文考虑了多用户多窃听、抗干扰通信的情景，综合应用了IRS、波束成形、AN等关键技术，考虑用户最小服务质量和不完美CSI，提出了一种干扰和窃听场景下的鲁棒资源分配算法，以应对复杂通信环境带来的技术挑战。本文的主要贡献总结如下：

(1) 针对恶意干扰下的多用户、多窃听IRS辅助安全通信场景，考虑了非法节点的不完美CSI和干扰器未知波束成形向量。基于有界信道误差模型，在最小安全速率，IRS相移，最大发射功率约束下，构建了一个联合优化BS波束成形向量、IRS相移矩阵、AN协方差矩阵的和安全速率最大化鲁棒资源分配问题。该问题由于引入了不确定参数，是一个无限维约束的非凸优化问题，难于直接求解。

(2) 由于该问题是一个难以直接求解的非凸问题，所以首先通过松弛变量将目标函数中的凸差问题转化为不等式约束，然后利用连续凸逼近和泰勒级数展开处理其非凸性；对于不完美CSI采用S-程序法和符号定性法进行求解，未知干扰波束成形利用Cauchy-Schwarz不等式转化为可求解问题；对于约束在前几轮迭代难以满足的问题，采用罚函数法解决。

(3) 通过仿真结果和现有方法比较，证明了在干扰和窃听同时存在的情况下，使用AN和IRS能有效提高系统和安全速率、降低功率开销、提高抗干扰裕度，有效抵御恶意干扰和窃听行为，并提供更可靠、安全的通信环境。此外，与传统算法相比，本文算法提前考虑信道误差的影响，能够提高系统的鲁棒性和可靠性，大幅降低用户的保密中断概率。另外，本文对选择IRS反射单元最优个数提供了有价值的参考，并探讨了和安全速率与系统鲁棒性之间的权衡关系，为实际系统的部署提供了重要的参考依据。

符号说明：小写斜体表示变量； rank(Y),Tr(Y),YT,YH和Yn,n分别表示矩阵Y的秩、迹、转置、共轭转置和第n行第n列的值； diag(y)表示以向量y为主对角线元素的对角矩阵； |·|表示复数的模运算； ||·||2表示向量的2范数； ||·||F表示矩阵的F范数； CM×N表示M行N列的复数矩阵；IN表示N行N列的单位矩阵；0M×N表示M行N列的零矩阵。

2 系统模型和问题描述

如图1所示，本文研究的是IRS辅助的下行安全通信系统。其中，在恶意多天线干扰器和M个单天线Eve存在的情况下，多天线的BS通过直接链路和IRS反射链路向K个单天线用户传输信息。假设BS配备Nt根天线，同时IRS配备Nr个无源反射单元。另外，为了便于分析，系统中BS的天线、IRS的反射单元、窃听者和用户集分别定义为∀nt∈Nt≜{1,2,...,Nt},∀nr∈Nr≜{1,2,...,Nr},∀m ∈M≜{1,2,...,M},∀k ∈K≜{1,2,...,K}。

图1 系统模型

由于严重的路径损耗，本文只考虑IRS第1次反射的信号，而忽略IRS反射两次或两次以上的信号。BS到合法用户k的信道增益，BS到窃听者m的信道增益，BS到IRS的信道增益，干扰器到合法用户k的信道增益，干扰器到IRS的信道增益，IRS到合法用户k的信道增益和IRS到窃听者m的信道增益分别表示为另外，BS通过导频信号来估计信道[12]，可以准确地获取所有合法用户的CSI。然而，由于基站和第三方节点之间缺乏合作，非法信道的CSI很难获得，因此，采用有界信道误差模型来表征非法信道的CSI不确定性，具体表示为

BS在同一频带内同时给每个合法用户发送K个独立的数据流，此外假设M个窃听者可以独立地窃听任何数据流[13]。为了防止用户信息被窃听，在发射信号中加入AN信号，则发射信号x表示为

其中，wT,k ∈CNt×1表示BS发送给合法用户k的波束成形向量，sT,k表示BS发送给合法用户k的机密信息，且满足E {|sT,k|2}=1,z ∈CNt×1表示AN信号，且满足z～CN(0,Z),Z≽0是AN的协方差矩阵[5]。定义IRS的相移矩阵表示为Θ=diag(vH)，其中，v=[v1,v2,...,vNr]H,vn=ϕnejθn,ϕn ∈[0,1]和θn ∈[0,2π) 分 别表示IRS第n个反射元件的振幅系数和相移。为了便于分析，与现有工作类似[14]，本文设置ϕn=1,∀n ∈Nr。因此，用户k的接收信号可以表示为

根据式(3)，用户k的信干噪比可示为

如果窃听者m窃听第k条机密消息，则窃听者m收到的第k条消息的信干噪比可表示为

则窃听者m窃听第k个用户的速率表示为R=log2(1+γ) 。因此，用户k的安全速率可以表示为

在BS无法准确获取非法节点CSI且不知道干扰发射器的波束成形向量的情况下，考虑最坏情况下的安全通信，通过联合优化BS的波束成形向量{wk}k∈K, AN协方差矩阵Z和IRS的相移v来最大化系统和安全速率，以抵抗窃听和干扰攻击，从而保证系统安全通信，则优化问题表述为

其中， C1 是合法用户的服务质量约束，R是用户k的最小速率； C2为BS处最大发射功率约束，Pmax为BS最大发射功率； C3为IRS反射元件的相移约束。

3 交替优化算法求解

3.1 固定 v 求解 {Wk} 和Z

为了解决子问题1，首先引入松弛变量σk ≥0，将目标函数和 C1 约束中的γk重新表示为

其中，Jk=|()HwJ|2≤σk。由于干扰器的波束成形向量wJ未知，为了使问题在实际应用中可行，利用Cauchy-Schwarz不等式得到Jk的上界，即|()HwJ|2≤PJ||()H||2，其中PJ表示功率 ||wJ||2，利用信号强度和信道增益可以得到[15]。然而由于干扰器的不完美CSI，无法准确获得PJ，因此采取|PJ-|/PJ≤ξP来表示 ||wJ||2的估计误差，其中表示功率的估计值。通过变换可以得到/(ξP+1)≤PJ≤/(1-ξP) ，所以||()H||2≤=σk(1-ξP)/≤σk/PJ。为了处理不完美CSI，利用 Schur补定理[16]将其等价转化为式(9)

由于式(10)的多个不确定参数，因此引入引理1处理。

引理1(符号定性法)[17]定义矩阵B=BH和 {Ci,Di}，当且仅当∀i,ui ≥0时，线性矩阵不等式：,∀i,||Xi||≤ζi成立，则有

因此，式(10)可以转化为式(12)

其中，uk,1≥0,uk,2≥0是引入的松弛变量，定义u={uk,1,uk,2,σk|∀k} 。为了处理目标函数和 C1中速率的非凸性，考虑使用变量松弛为

其中，φk,ηk,rk,βk,m,αk,m,τk,m是松弛变量，然而式(13)、式(14)仍然是非凸约束，为了解决式(13)和式(14)的非凸性，利用逐次凸逼近(Successive Convex Approximation, SCA)和泰勒级数展开[18]，式(13)、式(14)近似为

由于信道不确定性的影响，式(17)、式(18)属于无限维优化问题，关键的挑战是将其转化为确定性问题。因此，对于式(17)，首先将其展开为

再将式(21)中信道估计向量和信道估计误差向量单独分离，改写为式(22)

然后用引理2来处理式(22)中的CSI不确定性。具体来说，式(22)中每个用户对应的约束可以通过设置引理2中的参数进行重铸。

引理2(S-程序法)[19]定义变量x ∈Cn×1的2次函数：fi(x)=xHAix+2Re{x}+ωi,i=0,1,...,P，其 中Ai=。当且 仅 当∀i,λ ≥0时，{fi(x)≥0}⇒f0(x)≥0成立，则有

此时可以得到

其中，λk,m ≥0 是 引入[的松弛变量，ζΔhm=ζhBmE+ζhRmE。同理，式(18)可以表示为]式(26)

其中，ρ1是惩罚因子，当ρ1足够大时，会优先满足最小安全速率约束，当迭代结束时，ψ小于某个趋近于0的正值，说明能够满足约束，反之则说明当前可用资源下无法满足最小安全速率约束。

3.2 固定 {Wk} 和 Z 求解v

为了分离式(15)和式(16)中的相移矩阵，使用类似式(21)-式(23)的方法将式(15)-式(16)重新表示为，其中

则有

此时子问题2可以表述为

对于上述问题中的 C9约束采用与子问题1相同的SDR方法处理。对于3采用罚函数法，则式，非凸部分1≤|Vnr,Nr+1|2,nr=1,2,...,Nr可以近|Vnr,Nr+1|2=1,nr=1,2,...,Nr的等价形式为1≤|Vnr,Nr+1|2≤1,nr=1,2,...,Nr，根据1阶泰勒不等似为 |v|2-2Re{Vnr,Nr+1v}≤-1,nr=1,2,...,Nr，其中v(n)表示第n次迭代中获得的最优解。根据罚函数法的框架，在单位模量约束的等价约束上使用松弛变量L=[l1,l2,...,l2Nr]T， 将问题 (P4)重新表述为

其中，ρ2是惩罚因子，问题 (P5)是个凸SDP问题，可以使用CVX工具箱求解。因此，可设计如算法1所示基于迭代的和安全速率最大化算法。

4 复杂度分析

为了充分体现算法性能，进行如下复杂度分析。针对2阶锥(Second Order Cone, SOC)和线性矩阵不等式(Linear Matrix Inequality, LMI)凸优化问题的复杂度可以表示为[22]

其中，x¯ 表示LMI的个数，ci表示第i个约束对应的维数，y¯ 表示SOC约束的个数，e表示SOC约束对应维数，n是需要优化的变量个数。因此问题(P3)的复杂度可表示为式(39)

其中，n1=K+8KM+10K+。问题(P5)的复杂度可以表示为式(40)

其中，n2=(Nr+1)2+8KM+9K+2Nr+1。

5 仿真结果与分析

在本节中，通过仿真结果来评估所提出算法的有效性。假设一个配备Nt=8 的BS，Nr=8的IRS，干扰器的天线数为L=4。另外，BS, IRS和干扰器分别位于 (0 m, 0 m) , (50 m, 10 m)和(120 m, 5 m)。所有用户和Eve随机分布在一个圆心为 (70 m, 0 m) 和 (40 m, 0 m)，半径分别为5 m的圆内。假设信道模型包括大尺度衰落和小尺度衰落，大尺度衰落模型为 PL=-PL0-10ρlg(d0)，其中ρ为路径损耗指数，d0为链路距离，单位为m。PL0为1 m距离的路径损耗，其中 PL0=-40 dB，对 应 的 路 径 损 失 指 数 设 为ρBR=ρJR=2,ρBU=ρJU=ρBE=2.2,ρBU=ρJU=ρBE=4。小尺度衰落服从瑞利衰落。定义信道的归一化误差上界ξhRmE=ξhBmE=ξh=ξGJR，由ξh=ζh/||h||2给出。其余重要仿真参数设定为：m==-80 dBm,Pmax=30 dBm,PJ=20 dBm,ξP=0.01,R=0.5 bit/(Hz·s),K=M=2。

算法1 基于迭代的和安全速率最大化算法

图2给出了使用所提算法的和安全速率收敛图。从中可看出本文算法在经过大约25次迭代后就可以收敛，具有较好的收敛性。同时，系统的和安全速率随着BS天线个数增加而增加。因为越多的天线意味着波束成形效果越好，从而提高系统的和安全速率。同时可以看出IRS反射单元个数增加对收敛性的影响相较于天线个数增加对收敛性的影响更大，对比求解波束成形向量时只与IRS相移矩阵有关，求解IRS相移矩阵时不仅与波束成形向量有关，还与IRS相移矩阵的前一次迭代的值有关，所以IRS反射单元个数对收敛速度的影响远大于天线个数对收敛速度的影响。

图2 和安全速率收敛图

图3给出了不同算法和安全速率与基站最大发射功率之间的关系。从中可以看出，当最大发射功率较小时，无AN算法的性能和本文算法的性能相近。但随着发射功率的增加，无AN算法的和安全速率提升明显小于其他算法。这是因为在发射功率较低时，将有限的发射功率分配给用户的数据传输可以快速提高和安全速率。但是随着功率的增加，将功率直接分配给用户对和安全速率的提升效果逐渐降低。此时，可以通过分配功率给AN来降低窃听者的信干噪比，进而提高系统的和安全速率。因此，在高功率下，使用AN的算法可以更好地提升系统的安全性能。

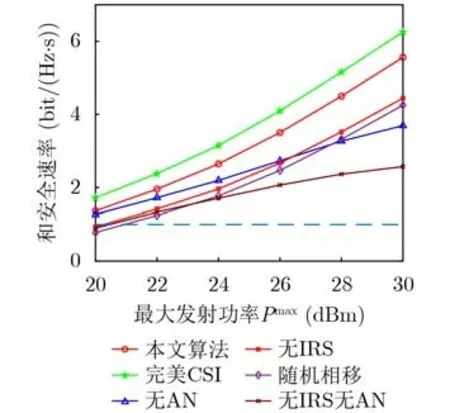
图3 最大发射功率与和安全速率的关系

同时，从中可以看出，使用IRS和AN可以减小最小功率开销，在R=0.5 bit/(Hz·s)时，随机相移算法、无IRS算法和无IRS无AN算法要抵抗20 dBm的干扰，至少需要约22 dBm的发射功率，否则将无法满足最小安全速率约束，而其余算法在使用20 dBm的发射功率时依然可以满足最小安全速率约束。

图4给出了IRS反射单元个数与和安全速率的关系。从中可以看出，除IRS随机相移算法外，其余算法的性能随着反射单元个数增加而提高，因为越多的反射单元可以引入更多的可控信道，从而重新配置无线传播环境。同时，可以看出随着IRS反射单元个数的增加，和安全速率的提升速率会逐渐降低，并且IRS随机相移算法的和安全速率随着IRS反射单元个数增加反而降低，且低于无IRS算法，这是因为IRS反射单元个数增加不仅会增加系统的和安全速率，同样会添加更多不完美CSI的窃听信道，同时也增加了干扰功率，BS需要消耗额外的通信资源来补偿由信道不确定性和干扰功率增加所造成的性能损失，这时如果仅仅添加IRS反射单元个数而不进行相移优化反而会降低通信质量，在实际部署时需要从需求、成本等方面综合考虑，选择最优IRS反射单元个数。

图4 IRS反射单元个数与和安全速率的关系

图5给出了和安全速率与干扰功率PJ的关系。从中可以看出，无论是IRS还是AN，均能显著提高和安全速率。此外使用IRS和AN可以提高系统的抗干扰裕度，在Rkmin=0.5 bit/(Hz·s)时，相比较无AN算法和无IRS无AN算法，其余算法能够抵抗至少30 dBm的干扰，而无AN算法只能抵抗约28 dBm的干扰，无AN无IRS算法只能抵抗26 dBm的干扰，超过28 dBm(或26 dBm)时将无法满足最小安全速率约束。

图5 干扰功率与和安全速率的关系

图6给出了不同算法的和安全速率随着窃听者个数增加而变化的情况。从中可看出，随着窃听者个数增加，系统的和安全速率降低，这是因为窃听者个数增加，需要消耗更多的资源满足最小安全速率约束，另一方面窃听者的信道是不确定的，BS越多需要更多的资源弥补信道不确定带来的影响。同时可以看出，无AN算法和安全速率的下降速率比无IRS算法更缓慢。因为AN虽然可以大幅降低窃听者的信干噪比，但是建立在额外功率开销的基础上。在应对窃听数量提升时，BS能够使用的功率又是有限的，所以无IRS算法下降速率较快。而IRS利用的是被动反射波束成形，不会有额外功率开销，每一个窃听者都会引入独立的反射信道，所以无AN算法变化相对较慢。

图6 窃听者个数与和安全速率的关系

图7给出了窃听者不同分布与和安全速率的关系。其中，距离d表示用户分布的圆心与窃听者分布的圆心之间的距离，角度α表示用户分布的圆心与BS的位置、窃听者分布的圆心之间连线顺时针方向夹角，仿真中用户分布的圆心为(25 m, -50 m)。从中可以看出，当窃听者距离BS比用户距离BS更近时，距离d对和安全速率的影响较小，但窃听者与BS的距离比用户距离BS更远时，距离d越大防窃听效果越好。同时，当角度α接 近 0.25π时，窃听者处于最优窃听位置，即处于BS和IRS中间，这种情况下防窃听效果最差。

图7 窃听者分布与和安全速率关系

图8给出了最小安全速率与和安全速率的关系，仿真中K=8。从中可以看出，系统和安全速率随着R的增加缓慢下降，因为随着R增加，系统需要更多的资源去提升较差通信链路用户的安全速率，以满足最小安全速率约束。

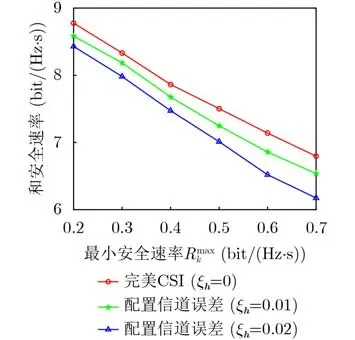
图8 最小安全速率与和安全速率的关系

图9给出了不同信道误差参数的抗中断能力，仿真中K=8。其中，保密中断表示，对当前配置参数下计算出的最优结果，在 Δh取实际误差上界内任意值的情况下，系统中任意用户不满足最小安全速率的情况。结合图8可以看出，在考虑ξh=0.01时，仅牺牲平均不到3%的和安全速率就可以降低平均35%的保密中断概率。提前考虑信道误差的虽然会牺牲一部分系统性能，但会大幅提高系统的鲁棒性。并且在参数配置时考虑的误差上界越大，中断概率越低，鲁棒性更强，但相应的和安全速率也会略有下降。在实际部署时可以根据实际信道环境，选择合适的参数配置，获得最优的系统性能。

6 结论

针对无线通信系统鲁棒性低、易受干扰和窃听的问题，本文提出一种IRS辅助的抗干扰安全通信系统鲁棒资源分配算法。在多用户、多窃听的情况下，考虑用户最小安全速率、最大发射功率和IRS相移约束，利用AN和波束成形优化系统最大和安全速率。对于问题的非凸性，利用连续凸逼近、泰勒级数展开法、S-程序法、符号定性法和罚函数法，将原问题转化成可以处理的凸问题。仿真结果表明，所提出算法具有较强的安全性和鲁棒性。