圆孔工字型蜂窝梁扭转模态自由振动研究

黄 斌, 张文福

(南京工程学院 建筑工程学院,南京 211167)

工字型截面蜂窝梁通过对工字型或H型截面梁切割、交错焊接而成,相较于原普通梁,蜂窝梁腹板高度增大,提高了腹板面内梁整体抗弯刚度。腹板开洞除了降低了材耗,可允许管线贯穿,因此梁高增大不会显著压缩建筑使用空间。另外,腹板开孔点缀了构件外观,在一定程度上起到建筑装饰作用。由于上述优点,蜂窝梁在工业厂房、文娱公共建筑等工业民用建筑中使用广泛[1-3]。目前,针对蜂窝梁静力性能已有比较丰富的成果发布,包括整体弯曲屈曲承载力[4-6],弯扭屈曲性能[7-8],腹板局部屈曲性能[9-13]等方面的研究。对于动力性能,已有学者开展了开口矩形板自由振动特性研究[14],而对于蜂窝梁构件扭转模态振动分析则鲜有报道。

对于蜂窝梁弹性阶段的动力性能分析,通常将其视为线性多自由系统,开展模态分析是应用叠加法求解构件动力响应的基础[15-17]。对于扭转刚度较小的构件,扭转模态圆频率较小,属于低阶模态之列,这意味着在总体响应分析中扭转变形贡献不可忽视。现阶段,对于薄壁构件扭转性能描述,无论是采用平衡法建立平衡微分方程,还是采用能量法建立扭转模态的能量泛函,均基于Vlasov所创立的薄壁构件约束扭转理论(后文简称传统理论)[18]。建立平衡微分方程则涉及到与翘曲双力矩相关的弯扭力矩,能量泛函模型则需要考虑翘曲正应力及约束扭转剪应力对应能量项。传统理论的突出特点是引入了扇型面积坐标,使得公式表达形式简洁工整,特别是翘曲双力矩与翘曲正应力,及弯曲力矩与约束扭转剪力的对应关系,甚至可分别与梁的弯矩与正应力,剪力与剪应力公式形式相比拟。传统理论适用于单一均质材料构件,对于处于弹塑性阶段或复合材料薄壁构件扭转性能描述,则显出不足。此外,对于不规则截面薄壁构件扭转性能描述,在确定主扇型坐标极点、零点,及相应截面模型量如主扇型惯性矩(翘曲常数),主扇型静面矩时计算繁琐,通常选用数值计算方式。

2014年,张文福等[19-23]提出了一种不同于传统理论的薄壁构件扭转性能描述的思想体系,将其命名为“板-梁理论”(后文简称板-梁理论)。由于该理论应用Euler-Bernoulli梁(Timoshenko梁)和Kirchhoff板模型先获得组成构件的各板条应变能,进而加和求得构件总应变能及动能。对于扭转变形模态,建立能量泛函模型过程中,不再涉及扇型坐标运算,这是板-梁理论相对传统理论的显著优势。同时,板-梁理论以板条作为基本分析单元,对于复合材料构件,处于弹塑性状态的构件,及组合截面构件扭转性能的研究分析具有较强适用性。目前,已成功应用于钢-混组合薄壁构件的扭转,工字梁弹-塑性弯扭屈曲问题,预应力钢梁弯扭屈曲的等问题解析解的推导。

本文针对圆孔工字型蜂窝梁,应用板-梁理论,推导圆孔工字型蜂窝梁扭转模态自由振动的应变能和动能,从能量等效角度构建一种连续型模型,明确构件扭转自由振动能量泛函,并依据Hamilton原理,获得平衡微分方程模型。基于模态试函数,求解扭转自由振动圆频率,并与数值计算结果进行了比对校验。本文连续型模型及其对应的能量泛函模型和平衡微分方程模型的构建过程能为不同开孔类型蜂窝梁提供直接参考。

1 能量泛函模型

两端简支(夹支)的圆孔工字型蜂窝梁模型截面几何尺寸如图 1所示,密度为ρ,弹性模量为E,泊松比为υ,所有基本材料物理参数沿梁长(L)均匀分布。

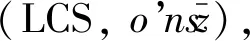
1.1 上翼缘能量

1.1.1上翼缘板面内位移相应应变能及动能

当构件发生扭转变形模态时,整体坐标系下,截面上翼缘任意点(x,y)处的位移矢量为

(1)

根据坐标转换原则,整体坐标下的矢量分量(x,y)在局部坐标系下可表示为

(2)

局部坐标系下位移分量表达如式(3)所示。

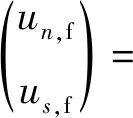
(3)

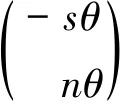
(4)

相应的应变及应力为

(5)

面内位移对应应变能则为

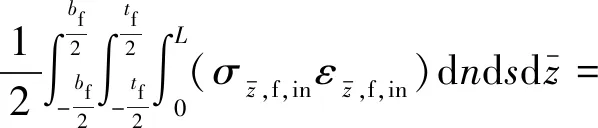
(6)

动能为

(7)

1.1.2 上翼缘板面外位移相应应变能及动能

对于上翼缘面外位移分量,已知板面外挠度un,f,out=un,f=-sθ,根据Kirchhoff薄板模型,可得(图3(b))

(8)

(9)

相应应变为

(10)

上翼缘面外位移分量相应应变能Uuf,out和动能Tuf,out分别为

(11)

(12)

式(6)与式(7)求和,以及式(11)与式(12)相加则可分别获得上翼缘总应变能和总动能,即

Uuf=Uuf,in+Uuf,out

(13)

Tuf=Tuf,in+Tuf,out

(14)

1.2 腹板能量

为便于构建蜂窝梁的等效连续性模型,将蜂窝梁拆分成 “Flange”,“Web1”以及“Web2”三部分,如图 4所示。“Flange”由上下翼缘组成,其相应应变能和动能已在2.1节完成讨论。“Web1”由腹板两条纵向连续板条组成,而“Web2”则是由不连续竖向板条组成。各分部截面几何参数如图 5所示。针对“Web2”,根据能量等效原则,将其等效为连续型薄板。将分别分析Web1和Web2相应能量。

腹板任意点(x,y)整体坐标系的位移可表示为

(15)

根据坐标转换关系,局部坐标系下分量则表示为

(16)

由于腹板的形心与构件截面形心重合,因此腹板位移平面内位移为零,式(16)中位移均为平面外位移。

根据Kirchhoff薄板模型,相应位移,应变分别如式(17)和式(18)所示。

(17)

(18)

1.2.1 Web1能量

已知腹板Web1板件的位移和应变分别如式(17)和式(18)所示。类比上翼缘板推导过程,可得Web1板件相应应变能(式(19))和动能(式(20))。在进行Web1分部板件能量积分时需注意根据相应截面几何尺寸(图5),调整积分限。

UCb,web1=UCb,web1,out=

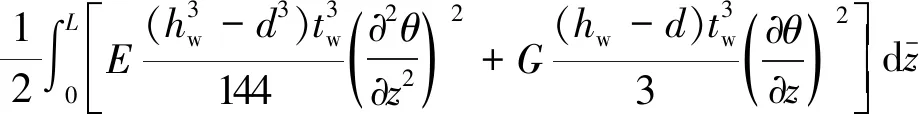
TCb,web1=TCb,web1,out=

(20)

1.2.2 Web2能量

由分析模型(图4)可知,腹板Web2分部是由不连续的竖向板条组成。选取Web2中的单个竖向板条作为分析单元(图6),根据能量等效,将不连续的Web2转化为连续薄板。建立Web2分析单元局部坐标系osζ,从而分析单元边界可表示为

(21)

每个分析单元的总应变能为

WU,Cb,web2=WU,Cb,web2,out=

σs,f,outεs,f,out+τsz,f,outγsz,f,out)dndsdς=

相应动能如式(23)所示

WT,Cb,web2=WT,Cb,web2,out=

(23)

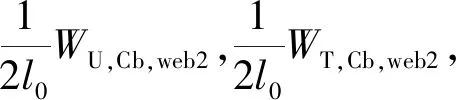
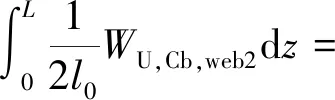
(24)

(25)

1.3 构件总能量

将翼缘应变能和动能分别与腹板应变能和动能相加可获得构件总应变能(式(26))和总动能式(27)。

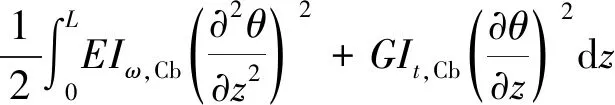
(26)

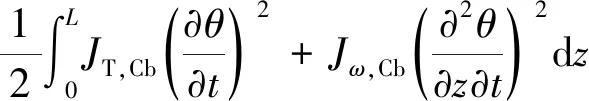
(27)

其中,

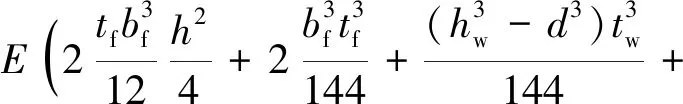
(28)

(29)

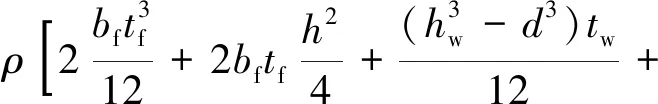
(30)

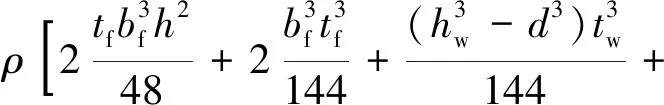
(31)

基于圆孔工字型蜂窝梁扭转模态自由振动总应变能式(26)和总动能式(27),根据Hamilton原理,可得总能量泛函模型

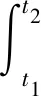
(32)

2 平衡微分方程模型

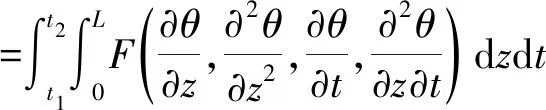
(33)

其中,

根据Euler-Ostrogradskii公式或变分运算,可推得平衡微分方程

对于两端简支边界条件,假定扭转模态试函数为

(36)

代入式(35)可得

(37)

(38)

相应频率则为

(39)

3 有限元分析

3.1 单元选择与划分数量

应用通用有限元软件ABAQUS(Version 2020)建立圆孔工字型蜂窝梁有限元模型,如图 7所示。采用S4R单元离散几何模型,此类型单元采用缩减积分方案,已成功应用于薄壁梁、柱模型的有限元分析中[24]。单元划分数量沿翼缘方向数量为22[25],腹板和纵向长度方向根据腹板高度与翼缘宽度比值,以及长度与翼缘宽度比值确定,据此可确保单元形状基本为方形,有利于提升计算精度和计算效率。

3.2 边界条件

采用MPC(multipoint constraints)约束命令将两端截面节点x、y向平动位移及绕z轴转动位移与截面形心点位移进行耦合,从而形成两端夹支支座。 跨中所有截面节点绕z轴转动位移耦合于截面形心以满足刚周边假定。跨中1/2长度处截面,约束节点z向位移,以消除z向刚体位移,如图7所示。采用上述边界条件设置方法,即可确保满足夹支支座要求,又可保证两端截面纵向纤维翘曲不受干扰。典型有限元模型扭转模态如图8所示。

3.3 有限元结果

3.3.1 扭转模态自由振动频率

有限元试件几何参数及数值与理论对比结果如表 1所示。由表1可知,扭转模态对应圆频率数值与理论结果比值平均值为0.976 8,标准差为0.004 1。因理论模型中完全考虑了刚周边假定,其圆频率结果较数值结果略大。总之两者比值结果表明了理论公式良好的预测精度。

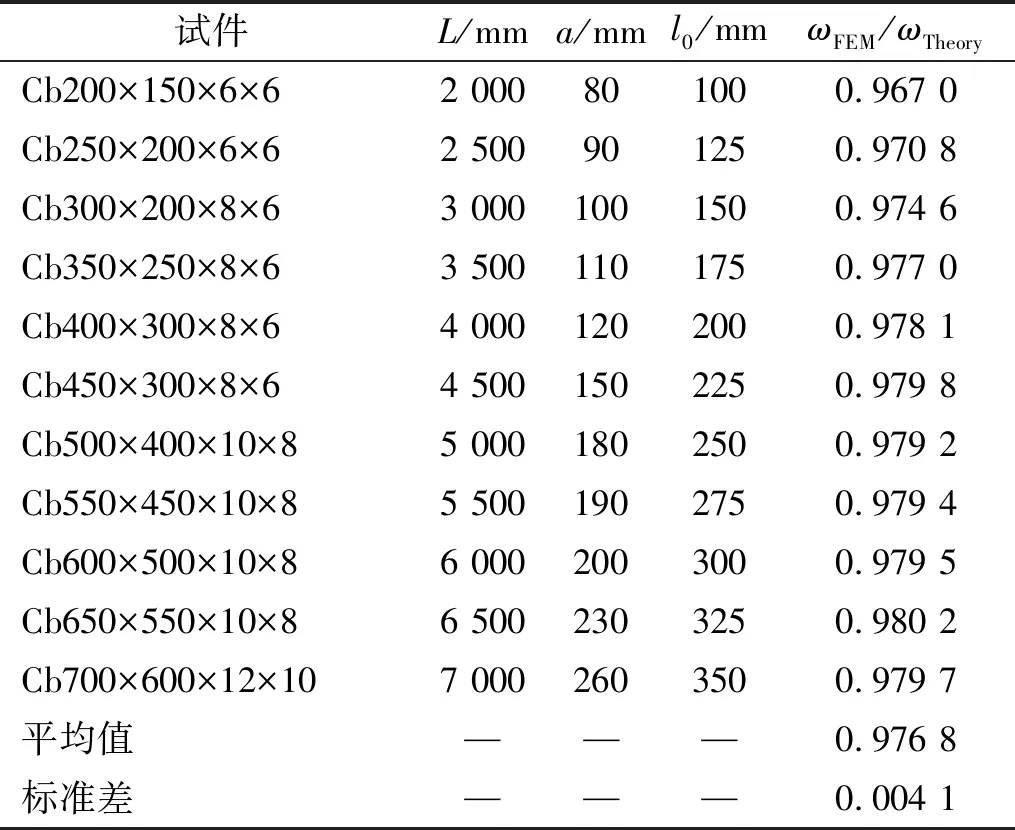
表1 振动频率数值结果与理论结果对比

3.3.2 扭转刚度和截面转角

通过能量变分模型确定的构件名义翘曲刚度(EIω,Cb),名义自由扭转常数(GIt,Cb)及名义转动惯量(JT,Cb)分别如:式(28)、式(29)及式(30)所示。为进一步检验理论推导结果的适用性,以悬臂蜂窝梁端部施加单位扭矩模型为研究对象(图9),开展构件端部转角的理论分析与有限元计算对比。悬臂梁基本参数如图1所示。对于悬臂梁端部作用单位扭矩,参照式(38)可得其平衡微分方程为

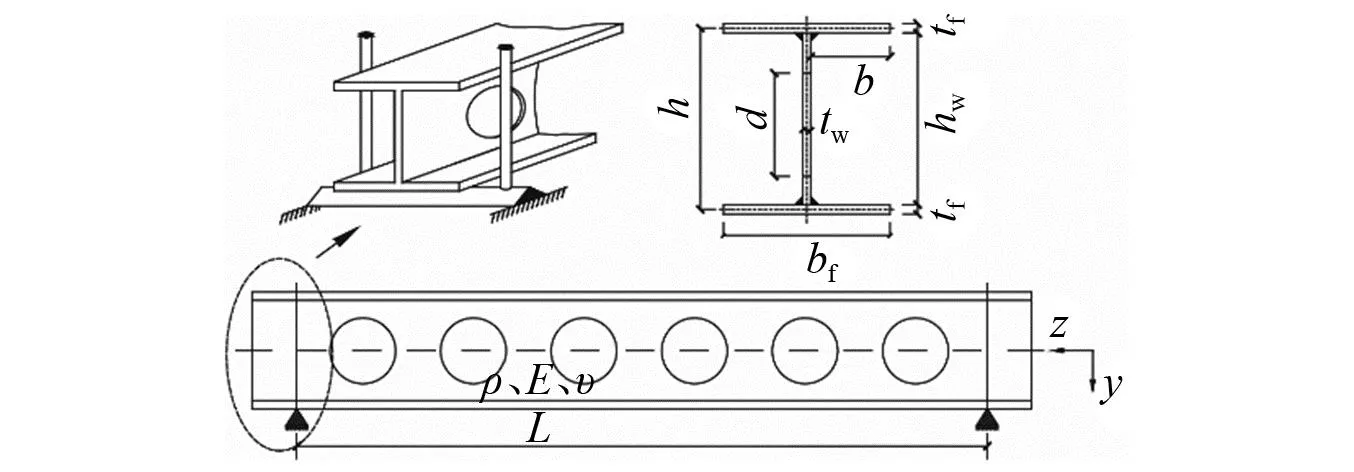
图1 圆孔工字型蜂窝梁模型基本参数Fig.1 Parameters of the circular opening I-section cellular beams

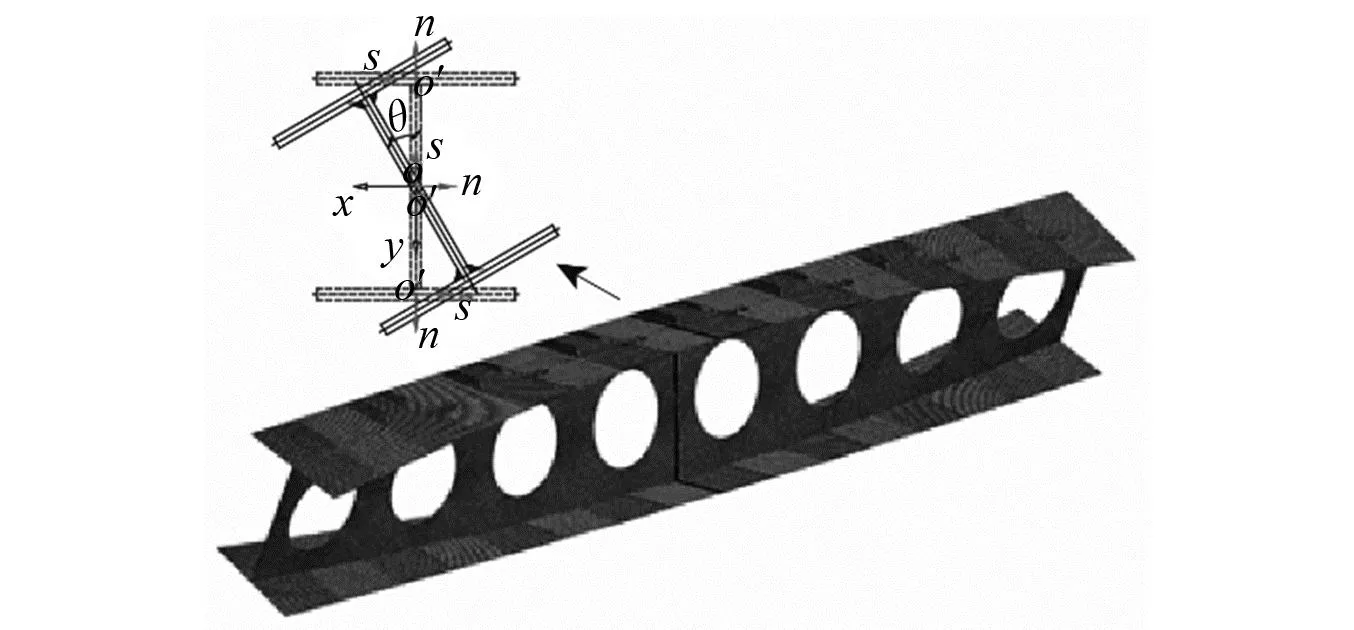
图2 典型扭转模态及坐标系Fig.2 Coordinate systems and typical torsion mode

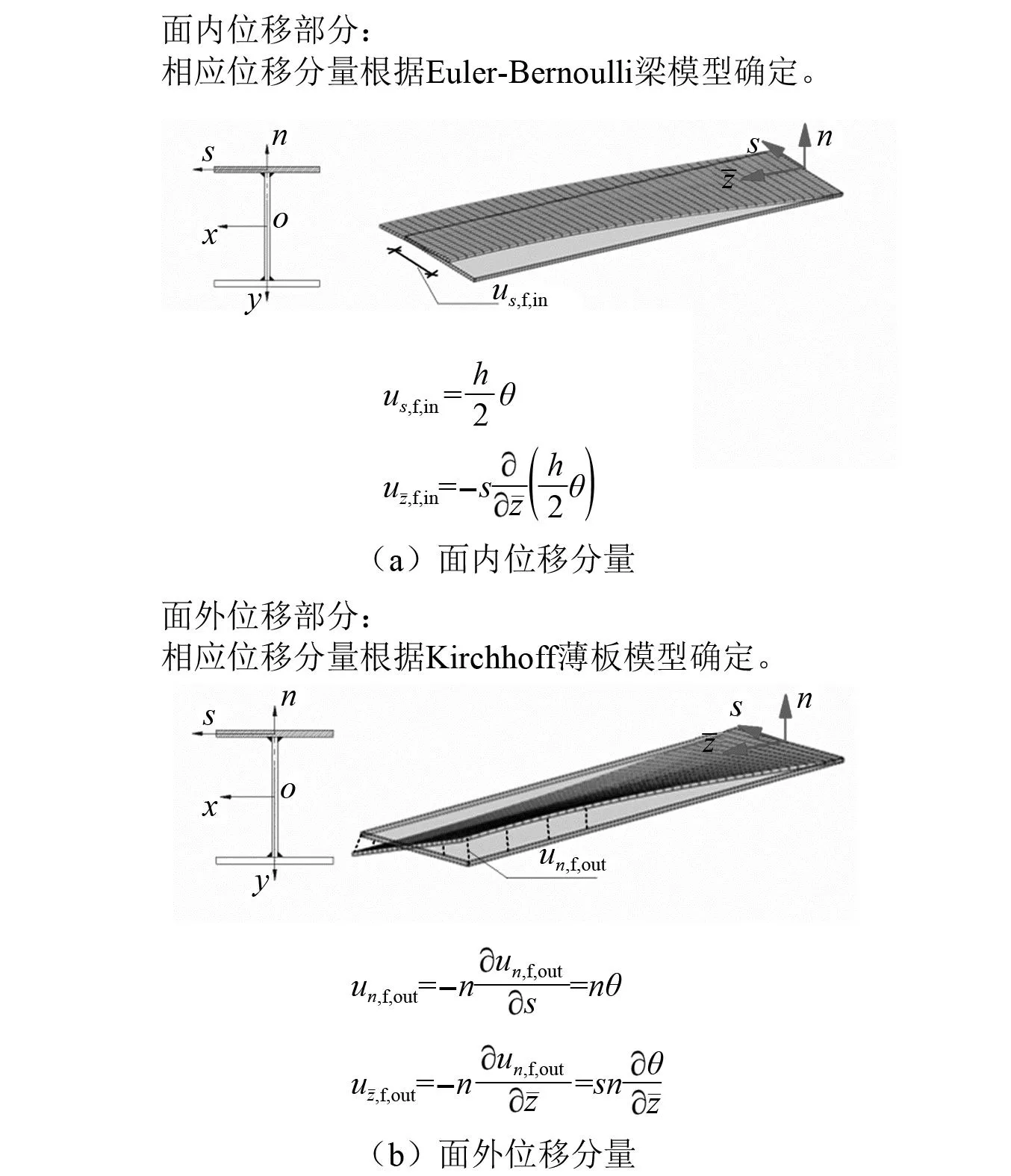
图3 基于板梁理论确定的上翼缘面内、外位移Fig.3 In-plane and out-of-plane displacement components of the upper flange using plate-beam theory

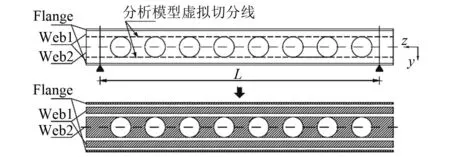
图4 工字型蜂窝梁分析模型Fig.4 Analytical model of the cellular beams

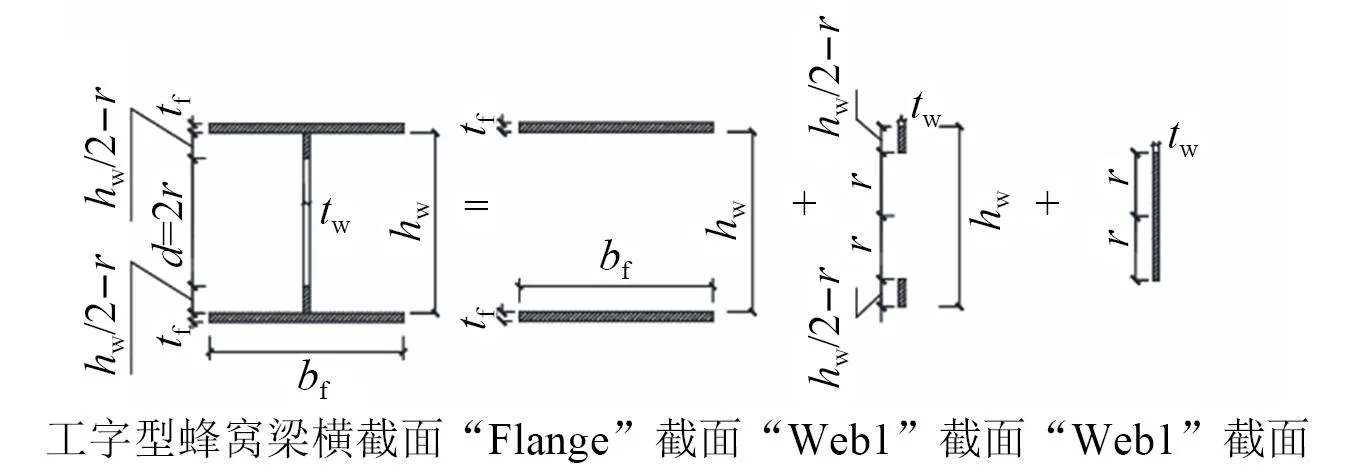
图5 各分部的截面几何尺寸Fig.5 Geometric dimension of the split parts of the cellular beams

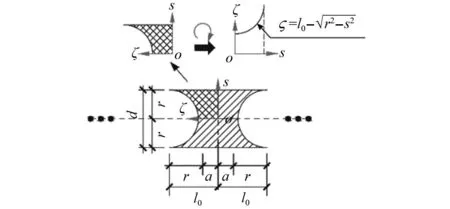
图6 Web2 分析单元Fig.6 Analytical element of Web2

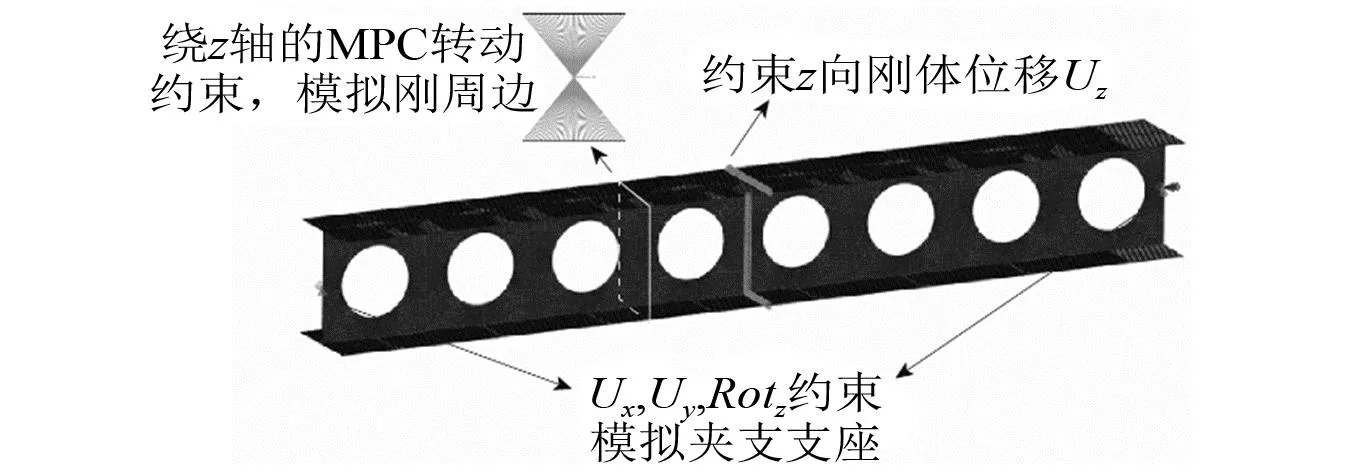
图7 典型圆孔工字型蜂窝梁有限元模型Fig.7 Typical finite element model of the circular opening I-section cellular beams

图8 典型圆孔工字型蜂窝梁扭转振动模态Fig.8 Typical torsion mode of the circular opening I-section cellular beams

图9 悬臂梁模型简图Fig.9 Cantilever beam model diagram

(40)

考虑边界条件,其解答为

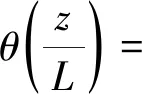
(41)

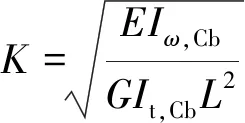
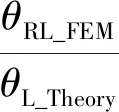
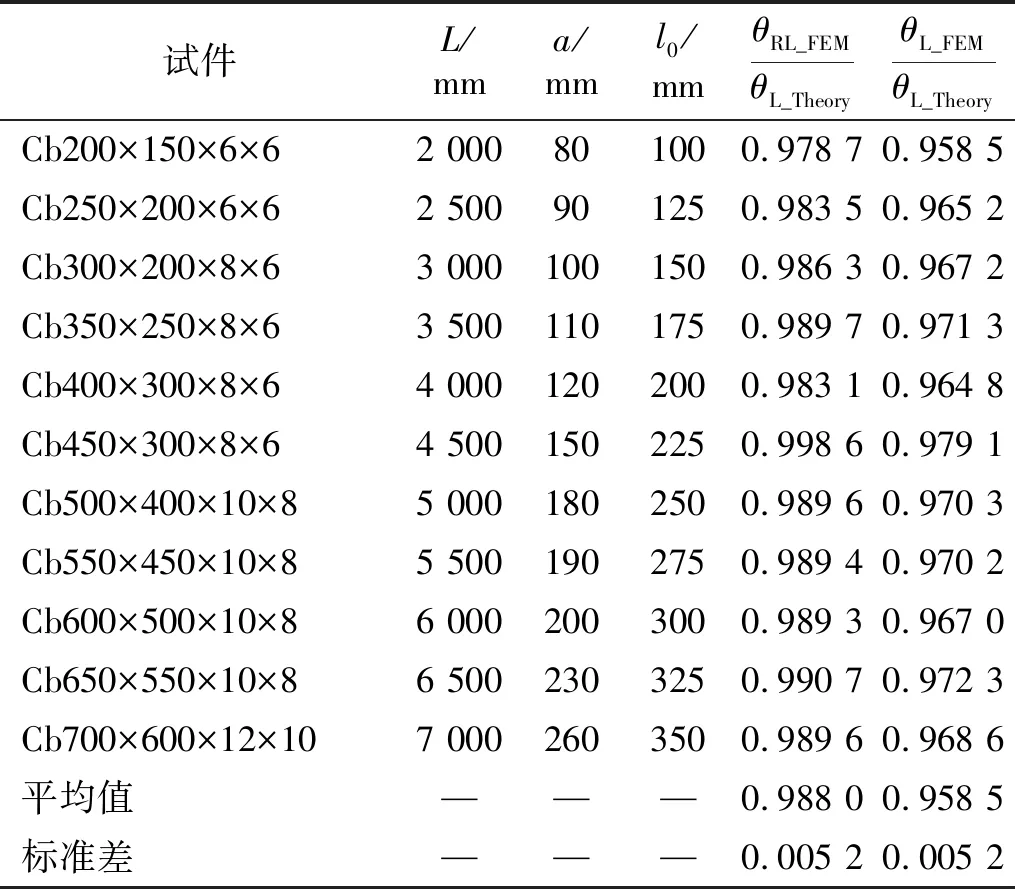
表2 端部截面转角理论分析与数值计算对比

4 结 论

基于板-梁理论思想,推导了能量泛函模型及平衡微分方程模型。针对夹支边界条件,假定了扭转模态试函数,进而获得了扭转模态圆频率,并与数值计算结果进行了对比校验。结论如下:

(1)从能量等效角度,提出了圆孔工字型截面蜂窝梁连续型模型,基于板-梁理论推导了构件应变能和动能。

(2)基于哈密顿原理获得了能量泛函模型,明确了圆孔工字型截面蜂窝梁的名义扇型惯性矩(翘曲常数),名义自由扭转常数及名义转动惯量等基本截面模量。通过变分运算建立了平衡微分方程模型。

(3)给出了两端简支圆孔工字型蜂窝梁扭转模态自由振动频率计算公式,理论结果与数值结果平均比值约为0.98,检验了理论公式的预测精度。

(4)开展了集中扭矩作用下悬臂工字型截面圆孔蜂窝梁端部截面转角的理论分析与有限元结果对比,结果表明理论结果与引入刚周边设置的数值计算结果比值平均值为0.988 0,与不考虑刚周边设置的数值计算结果比值为0.958 5,进一步检验了本文提出的蜂窝梁连续型模型及其扭转性能分析方法的可靠性。

(5)特别地,应用板-梁理论建立圆孔工字型截面蜂窝梁的能量泛函模型及微分方程模型的过程为其他开孔类型如方孔,六边形开孔工字型截面类型的扭转模态的自由振动理论分析提供了直接参考。