累计冲击荷载作用下GFRP-混凝土组合梁动态响应分析

杨丽辉, 周文波, 王 岩, 张浩天, 巩勋勋

(1.北京交通大学 土木与建筑工程学院,北京 100044; 2.中建玖合发展集团有限公司,北京 100000;3.建研院检测中心有限公司,北京 100013)

纤维增强复合材料(fiber reinforced polymer,FRP)作为一种新型建筑材料,与钢材相比,具有比强度高、抗腐蚀性强、受温度变化影响小等优点,能够大大减轻结构质量,提高结构的耐久性,有效地减少了后期的养护成本。在水下工程、海洋工程等中,FRP材料有着广阔的应用价值及发展前景[1-6]。

纯FRP造价高、弹模低、延展性差,为降低造价,充分利用FRP材料优异抗拉性能及混凝土材料抗压性能,科研人员开始研究FRP型材与混凝土材料的组合结构。FRP-混凝土组合梁因其成本效益高、抗弯性能卓越、质量轻、耐久性好等特点,成为主要的结构形式之一。王言磊等[7]对组合界面采用粗砂黏结的FRP-混凝土组合梁进行四点弯曲试验,发现采用黏结粗砂方式可有效传递组合界面剪力。薛伟辰等[8-9]提出了多种玻璃纤维复合材料(glass fiber reinforce plastic,GFRP)-混凝土组合梁的连接方式并对组合梁进行了弯曲试验研究,发现GFRP和混凝土间采用FRP开孔板或环氧胶连接均能有效提高二者工作性能,保证剪力传递。El-Hachar等[10]对CFRP及Settl FRP约束的GFRP-混凝土组合梁进行了弯曲试验,结果表明,组合梁比纯GFRP梁具有更高的抗弯强度和刚度。黄海林等[11-12]将GFRP-T形型材的上翼缘内嵌入混凝土中进行受弯性能试验,发现接触面喷砂及设置螺栓可以显著降低GFRP型材与混凝土板界面间的滑移。黄辉等[13]对3块 GFRP -混凝土组合连续板进行了静载试验,试验表明组合板具有良好的空间受力性能及变形协调能力。上述研究表明,在拟静力荷载作用下,FRP-混凝土组合梁具备较高的刚度、承载力等优势。

桥梁作为跨越山区天堑的重要结构物,在使用期限内因遭受到落石冲击作用引起结构损伤或失效的现象时有发生,造成了不可估量的人员伤亡及经济损失[14]。相较于静力荷载,冲击荷载加载速率高、冲击能量大,且混凝土材料的抗压强度、弹性模量等力学性能会表现出与静力荷载作用时截然不同的特性[15-17]。因此,对极具应用前景的FRP-混凝土组合梁进行落石冲击荷载下的动力响应研究显得尤为重要。

与静力荷载相比,冲击荷载具有发生频率低、应用范围受限、试验危险系数高等特点;且冲击荷载作用时间极短(通常为50 ms内),常规试验设备很难对结构动力响应进行捕捉,数据获取困难;同时科研人员对FRP-混凝土组合结构的力学特性还处于探究阶段,工程实践中应用较少,故现有针对FRP-混凝土组合结构动力抗冲击性能研究较为有限。Chen等[18]进行了冲击荷载作用下FRP板材与混凝土界面黏结性能试验。试验结果显示:FRP板材与混凝土间的界面黏结性能随着应变率的提高有所提高。Wang等[19]对中空的GFRP管以及填充了混凝土的GFRP管进行了竖向冲击试验,发现增加纵向纤维约60%,减少了两种试件的变形和破坏,空心GFRP管的冲击荷载峰值比GFRP管约束混凝土低约80%。Oasrawi等[20-21]对GFRP管约束混凝土梁进行了竖向冲击试验,结果表明GFRP管的存在能够有效地提高构件的抗冲击性能。Roudsari等[22]对GFRP布包裹的钢筋混凝土梁进行冲击试验及有限元模拟,研究表明对反复冲击荷载作用下的钢筋混凝土梁进行FRP加固可以有效提高其抗动力性能,减缓损伤发展。Zhang等[23]对FRP(Carbon FRP、Basalt FRP和Glass FRP)包裹及未包裹的钢管混凝土柱进行落锤冲击试验,结果表明FRP包裹可以改善其性能并提高其承载能力。何庆峰等[24-25]通过对无损RC(reinforced concrete)梁及CFRP加固冲击后的有损RC梁进行落锤冲击试验。试验结果表明,在保证CFRP与RC梁之间良好界面黏结性能下,CFRP能有效改善并增强构件的整体受力性能。

综上所述,目前FRP-混凝土组合结构抗冲击性能研究主要集中于FRP布/管约束混凝土结构或加固受损构件,而针对FRP-混凝土组合梁抗冲击性能的研究较少;在组合结构动力响应方面,现有研究多为组合结构在单次冲击荷载下的动力响应,对于结构在使用年限内可能受到的多次落石冲击荷载却鲜有涉及。多次冲击的累积效应可能会导致结构的逐渐削弱和失效,研究结构累计冲击可以了解结构在长期使用和多次冲击下的安全性和可靠性;并确定结构的抗冲击能力和破坏机制。为进一步了解FRP-混凝土组合梁在累计冲击荷载下的响应特征,本文对1根纯GFRP梁和4根GFRP-混凝土组合梁进行冲击试验,借助于高速摄影仪器及动态信号采集设备,获得了不同混凝土厚度及冲击方向下组合梁的累计冲击损伤演化过程及动力响应。借助于有限元分析ANSYS/LSDYNA软件建立了GFRP-混凝土组合梁精细化累计冲击模型,结合相应试验结果,对有限元模型进行了拟合修正,并基于该模型分析了冲击锤质量、冲击速度及构件截面高度比等参数对GFRP混凝土组合梁抗冲击性能的影响。

1 试验概况

1.1 试件设计

为研究GFRP-混凝土组合梁在冲击荷载下的动态响应,本文设计制作了1根纯GFRP梁(试件B0)、1根侧向冲击GFRP-混凝土组合梁(试件BT-150)及3根竖向冲击GFRP-混凝土组合梁(试件BV-120、BV-150、BV-180)。组合梁由下部受拉区GFRP方管和上部受压区的混凝土层组成。GFRP与混凝土界面采用施工方便、性价高的粗砂黏结法,在环氧树脂表面均匀黏结5～10 mm(非均匀粒径)的小石子,石子覆盖率为35%～45%。试件全长均为1 600 mm,净跨1 400 mm。GFRP方管横截面均为88.5 mm×88.5 mm。混凝土高度分别为31.5 mm、61.5 mm、91.5 mm。试验梁尺寸如表1所示。

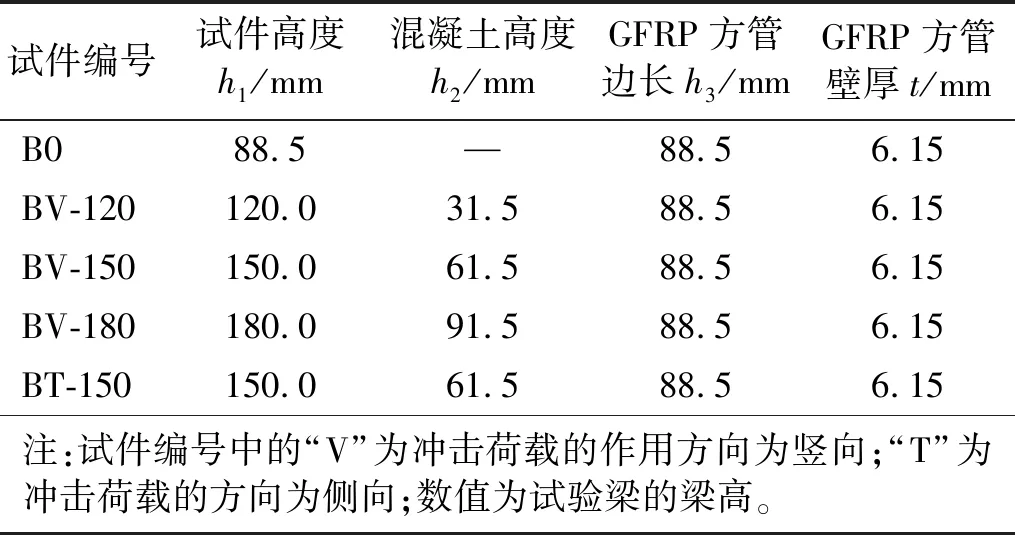
表1 试件规格表

试件所用混凝土设计强度等级C40,在试件制作时预留了标准混凝土立方体试块以测试混凝土抗压强度。GFRP型材密度为1 876 kg/m3。根据GB/T 1446—2005《纤维增强塑料性能试验方法总则》,对12个GFRP长方体试样(300 mm×25 mm×8 mm)进行强度试验,以测得试验所需的GFRP力学性能。试件制作过程中,先用砂纸打磨GFRP梁上表面,并用丙酮进行擦拭;后采用A级环氧胶(厚度约为1.5 mm)将粗砂粒均匀黏结在GFRP型材表面来对GFRP-混凝土界面进行粗糙处理(图1),操作完成后浇筑混凝土形成组合梁。材料力学性能如表2所示。

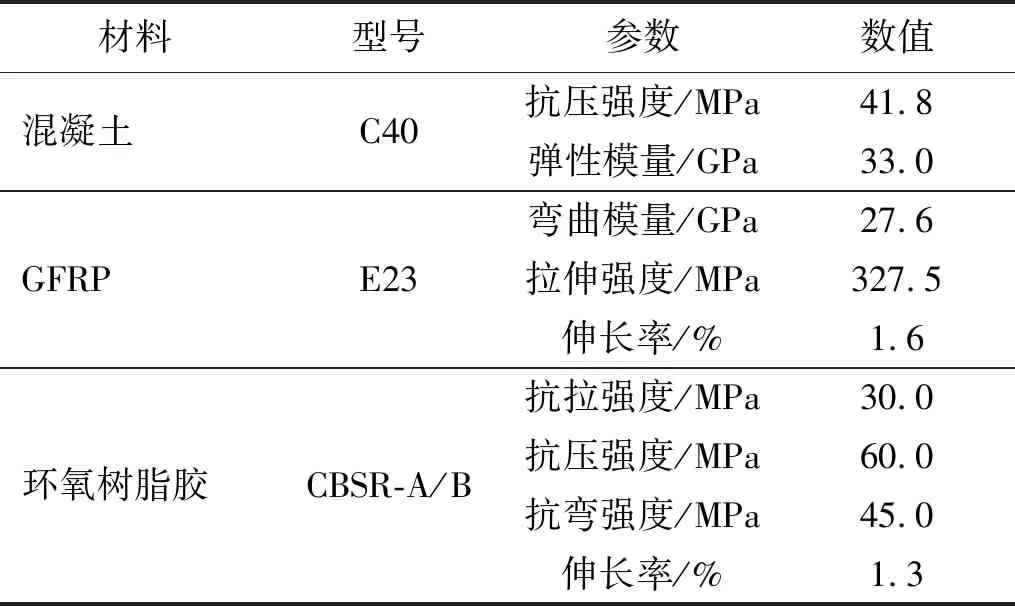
表2 材料力学性能

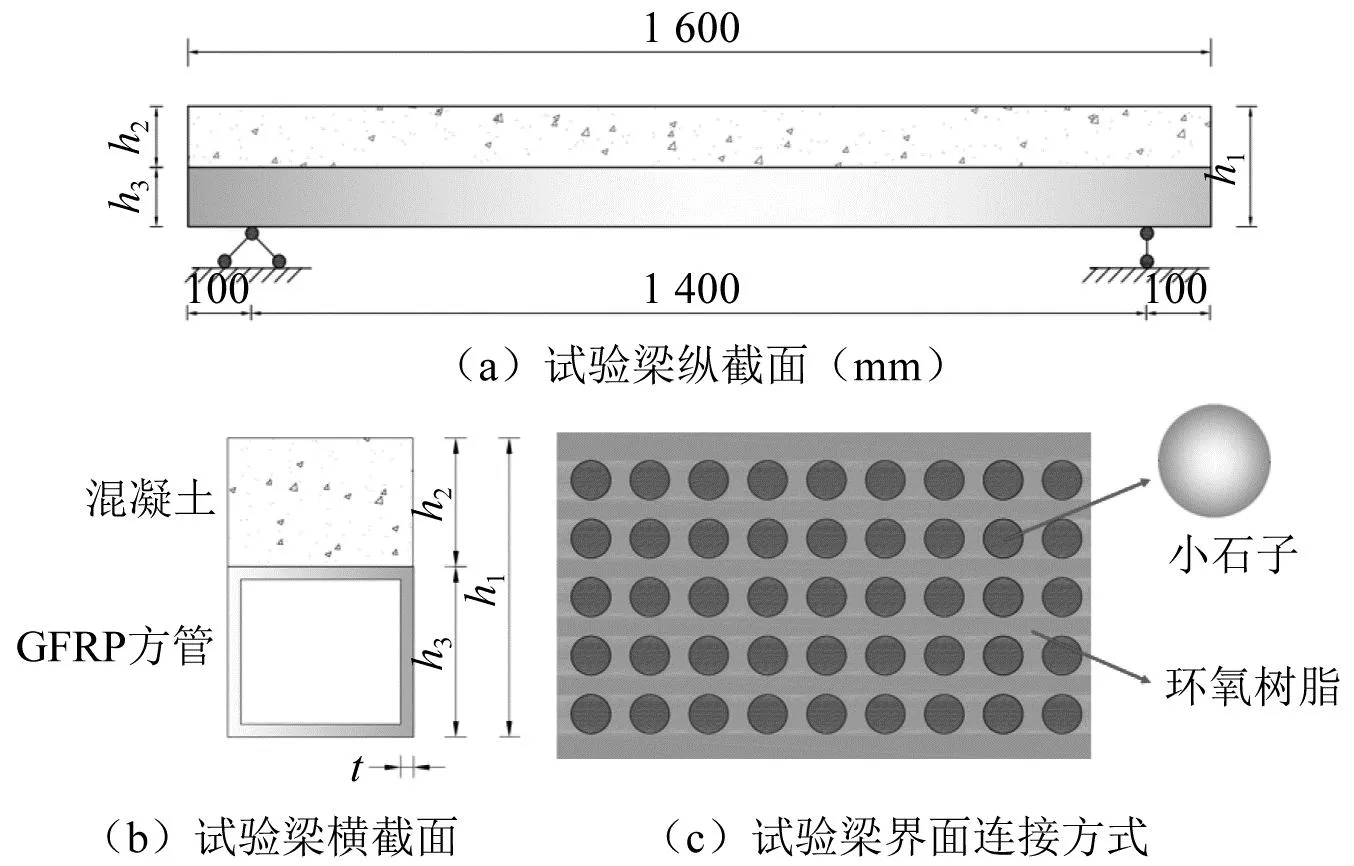
图1 试验梁横/纵截面及界面连接方式Fig.1 Test beam cross/longitudinal section and section connection method

1.2 试验方案

试验加载装置采用摇臂式落锤冲击试验系统,如图2所示。该系统分为:试验钢架、试件固定装置、冲击锤头、高度调节装置。试件固定装置中,支座部分设置简支约束。支座一侧焊接有螺纹钢筋、螺母及转动舵手。转动舵手可实现支座宽度的自由调节,通过预紧螺母可使侧边支座对梁体施加一定的预紧力,防止组合梁在冲击过程中跳脱。冲击锤头质量M为40.18 kg。试验中将试件的顶面跨中布置于冲击锤下,利用动力倒链将冲击锤头调节到设定高度(H)后释放即可对试件施加冲击荷载。

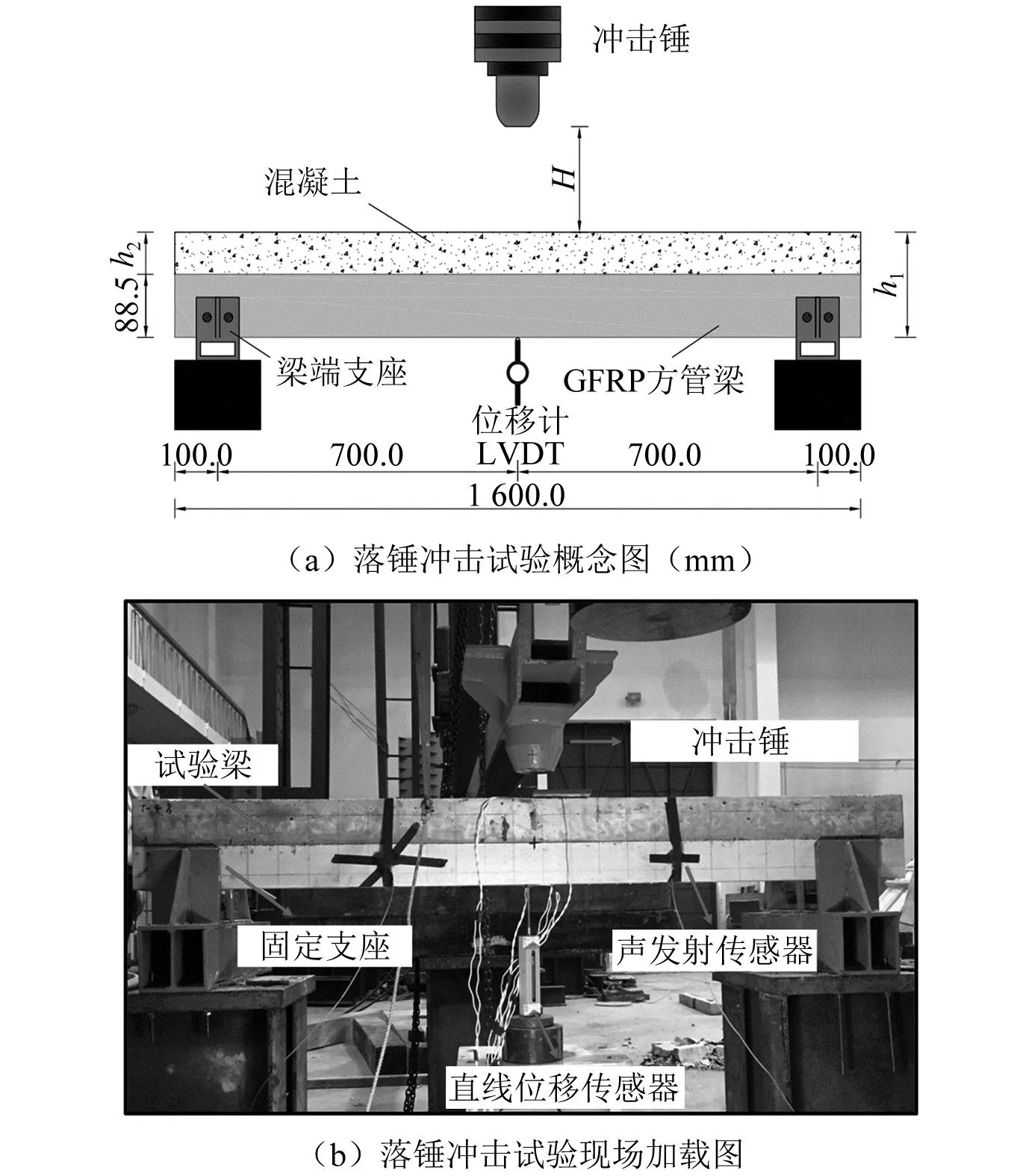
图2 落锤冲击试验装置Fig.2 Falling hammer impact test equipment

试验梁竖向和侧向加载示意图如图3所示。

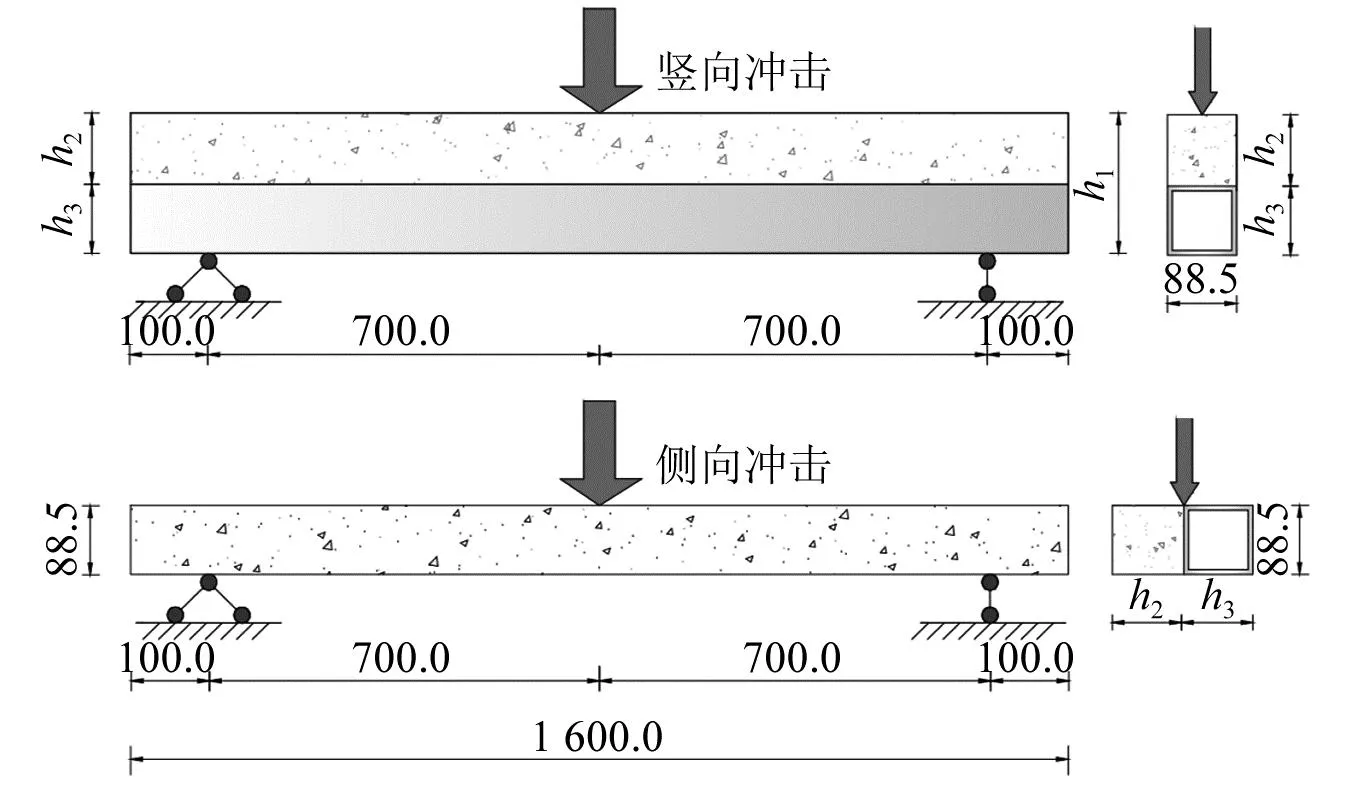
图3 试验梁竖向横向冲击示意图(mm)Fig.3 Schematic diagram of vertical transverse impact of test beam (mm)

试验设定加载高度H依次为5 cm、10 cm、15 cm、20 cm、30 cm及50 cm。试验过程中测取了试验梁所受的冲击力、跨中挠度、混凝土及GFRP跨中应变等数据,加载装置前侧布置高速摄影仪,监测冲击瞬时的裂缝开展与破坏过程,采集频率为100 fps。试验后,拍摄并绘制了冲击后的最终裂缝与破坏形态。

2 冲击试验结果及分析

2.1 裂缝发展

高速摄像机捕捉了试件从加载开始至完全结束的动态响应过程。对B0施加不同高度下的冲击荷载,在整个试验过程中,纯GFRP试件无明显塑性变形及损伤,说明GFRP材料具有良好的抗冲击性能,但随着冲击高度的增加,构件的变形响应不断增加,挠曲现象明显。

图4为各GFRP混凝土组合梁试件最终破坏形式。对BV-120、BV-150和BV-180施加竖向冲击荷载,组合梁均在冲击高度为20 cm时发生损坏;对BT-150施加侧向荷载,组合梁在冲击高度为30 cm时发生损坏。通过观察不同试验梁在冲击过程中的裂缝发展及破坏状态,具有以下共同特征:前三次(BT-150为前四次)冲击中组合梁的损伤均表现为混凝土裂缝的产生与发展,此时的裂缝均属于微裂缝,对组合梁的性能影响较小;在第四次冲击(BT-150为第五次)中组合梁上部混凝土出现贯通裂缝,混凝土退出工作。但不同工况下,混凝土的开裂及剥落状况存在较大差异,这主要与落锤局部接触状态以及碰撞区域混凝土刚度有关。

注:图4中数字为试验梁破坏时的冲击高度。

以BV-150试验梁不同冲击高度下梁体破坏过程为例,如图5(a)所示,在冲击高度为5 cm时,混凝土未产生裂缝损伤。当冲击高度为10 cm时,混凝土跨中底部右侧约10 cm位置处的剪跨区出现肉眼可见的轻微裂缝,裂缝高度至混凝土高约1/3处。当冲击高度为15 cm时,剪跨区裂缝迅速延伸,开展至混凝土梁顶部。当冲击高度为20 cm时,剪跨区裂缝发展成为主裂缝,混凝发生完全断裂,素混凝土退出工作。同时,观察梁体等位线可知,主裂缝右侧混凝土发生偏移,原因是混凝土与GFRP之间脱粘,二者丧失了共同工作能力,导致GFRP-混凝土组合梁抗冲击性能降低。当冲击高度为30 cm时,混凝土剪跨区产生新的贯通裂缝并伴随着混凝土顶部大面积破碎,局部呈现楔形破坏;当冲击高度为50 cm时,跨中两侧混凝土与GFRP彻底剥离,锤头下方混凝土由于垫板及GFRP挤压作用继续停留在梁体上。

为探究GFRP-混凝土组合梁在破坏荷载下的裂缝发展过程,根据高速摄影仪采集图片,对冲击高度为20 cm的组合梁冲击响应进行探究,如图5(b)所示。选取了0～100 ms时段进行分析,各时间节点裂缝形态如图2所示。在20 ms时,随着冲击锤对梁体上部混凝土进行挤压,剪跨区微裂缝(冲击高度为15 cm时产生的裂缝)得到进一步发展,混凝土产生破碎,伴随有少量新微裂缝形成;同时,裂缝右侧混凝土向右错动,与GFRP发生脱粘现象。在40 ms时,剪跨区主裂缝已发生贯通,冲击锤与梁体共同向上回弹,混凝土受到“惯性拉力”作用,主裂缝得到了进一步发展,混凝土继续向右错动,GFRP与混凝土间黏结效果大幅度降低。在60 ms时,梁体向下运动,混凝土受到“惯性挤压”作用,主裂缝宽度发生一定程度回缩。在80～100 ms时,梁体达到平衡位置,主裂缝宽度基本保持不变。

观察冲击荷载下组合梁裂缝宽度、长度、增长速度等不难发现:在冲击荷载下,混凝土从弹性阶段到破坏阶段所需时间较短;且随着冲击高度升高,梁体所受冲击能量增大,混凝土应变率随之提高,宏观表现为裂缝的长度与宽度开展。从梁体破坏状态来看,组合梁最终破坏表现为素混凝土断裂,裂缝右侧混凝土偏移,GFRP与混凝土剥离。因此,确保GFRP与混凝土间良好的黏结作用时二者共同工作的基础。

2.2 挠度时程曲线

为方便对比研究5根试验梁在整个冲击过程中梁体跨中位移变化,将各工况试验梁冲击挠度进行汇总(剔除加载间隙的准备时间),形成试验梁的跨中挠度时程曲线,如图6、图7所示。(注:图中数字表示冲击的加载次序)。

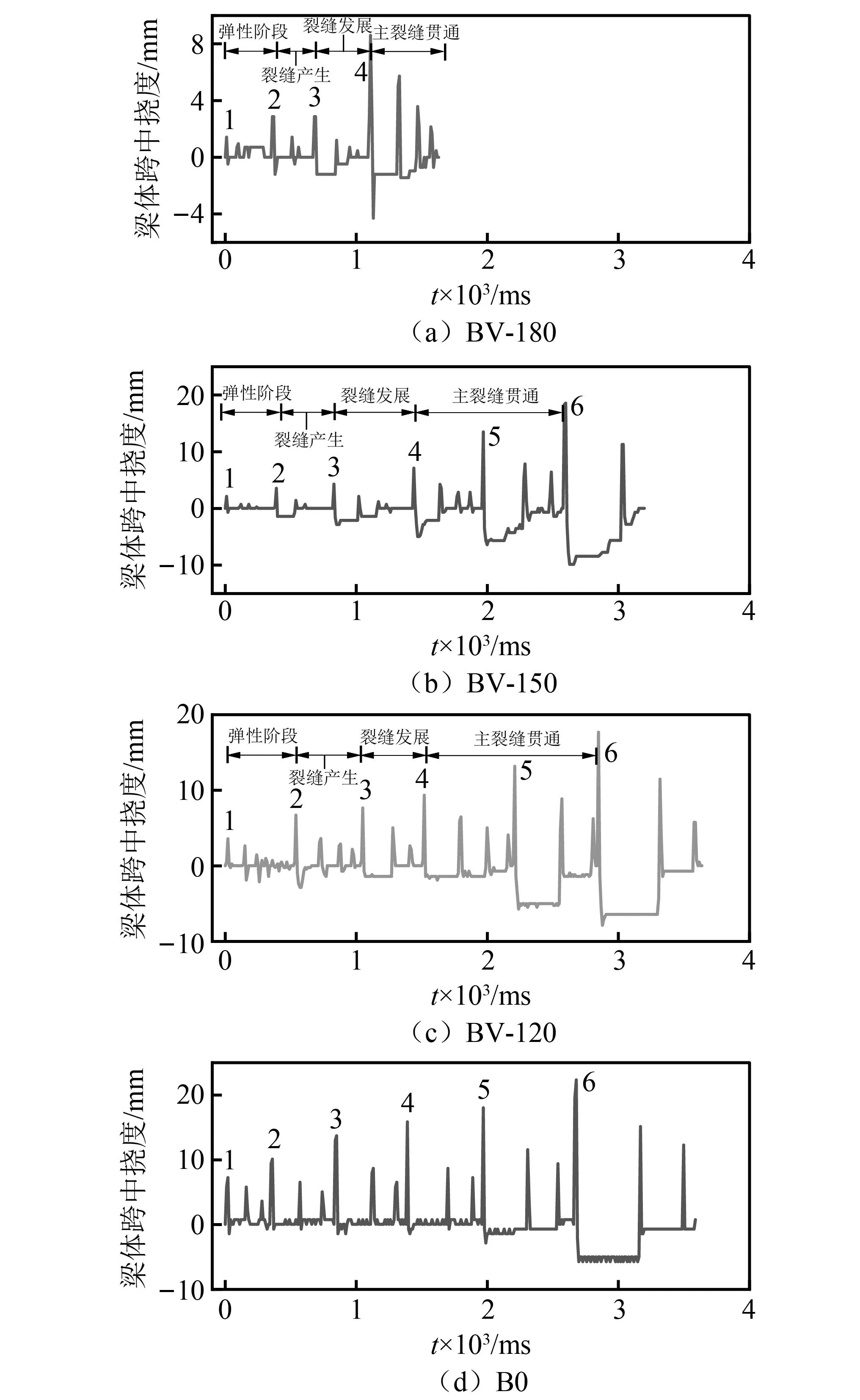
图6 不同混凝土厚度下梁体跨中位移时程曲线Fig.6 Time-distance curves of beam span displacement at different concrete heights

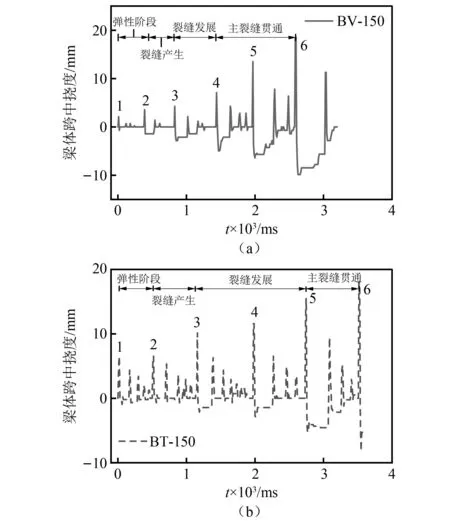
图7 不同加载方向下梁体跨中位移时程曲线Fig.7 Time-course curve of beam span displacement under different loading methods

图6为不同混凝土厚度下梁体跨中位移时程曲线。从各工况曲线可知,试验梁在冲击荷载作用下,会经历多次锤体冲击与自身回弹,且随着冲击能量的增大,梁体最大位移值逐渐提高。纯GFRP与组合梁相比,在相同冲击高度下,纯GFRP跨中挠度明显大于组合梁跨中挠度,其原因是GFRP材料的弹性模量及刚度较低,相同荷载作用下变形比组合梁大。BV-120、BV-150、BV-180相比,虽然三者损伤能量相同,但随着混凝土增厚,梁体刚度增大,并且在应力波的传播、衰减与反射过程中,混凝土吸收的冲击能量增多,使GFRP受到的冲击作用减小,故组合梁跨中挠度降低、自平衡能力更强。对比BV-120和BV-150在30 cm、50 cm冲击高度下的跨中挠度值,发现在同一冲击高度下两者挠度峰值相差不大,说明此时组合梁上部的混凝土均已退出工作,锤体冲击几乎全为下部GFRP承担,故将裂缝贯通作为组合梁破坏的标志是准确的。

图7为不同加载方向下梁体跨中位移时程曲线。当GFRP-混凝组合梁横向布置时,梁体高度相较于竖向布置更小,且GFRP对于刚度贡献程度更大,故侧向布置时刚度较小,在相同的冲击条件下BT-150的变形响应大于BV-150的变形响应。相反,由于GFRP参与梁体工作程度较高,侧向布置能够更大程度发挥GFRP自身优异的抗冲击性能,因此试件侧向布置耗散冲击能量的能力优于其竖向布置。

表3为各试验梁挠度响应汇总表。综合各试验梁破坏特征、挠度时程曲线及表3特征值可知:①纯GFRP本身具有优异的抗冲击性能,其刚度却远远小于各组合梁,在20 cm冲击高度下,挠跨比就已达到1/88.4;②混凝土厚度增大,能提高梁体刚度,同时在应力波的传播、衰减及反射过程中,混凝土吸收的较多的冲击能量,大大降低梁体跨中挠度(BV-120、BV-150、BV-180挠度降低程度分别为41.18%、51.99%、59.25%);BT-150耗散的冲击能量(315.04 J)比PBVS-150提高了60%,但其挠度降低程度远小于PBV-150,仅为26.91%;③各组合梁冲击过程可分为弹性阶段、裂缝产生、发展及贯通四阶段;破坏类型均为主裂缝贯通,GFRP与混凝土界面发生剥离。因此,在实际工程应用中,应特别注重GFRP-混凝土之间的黏结性能。

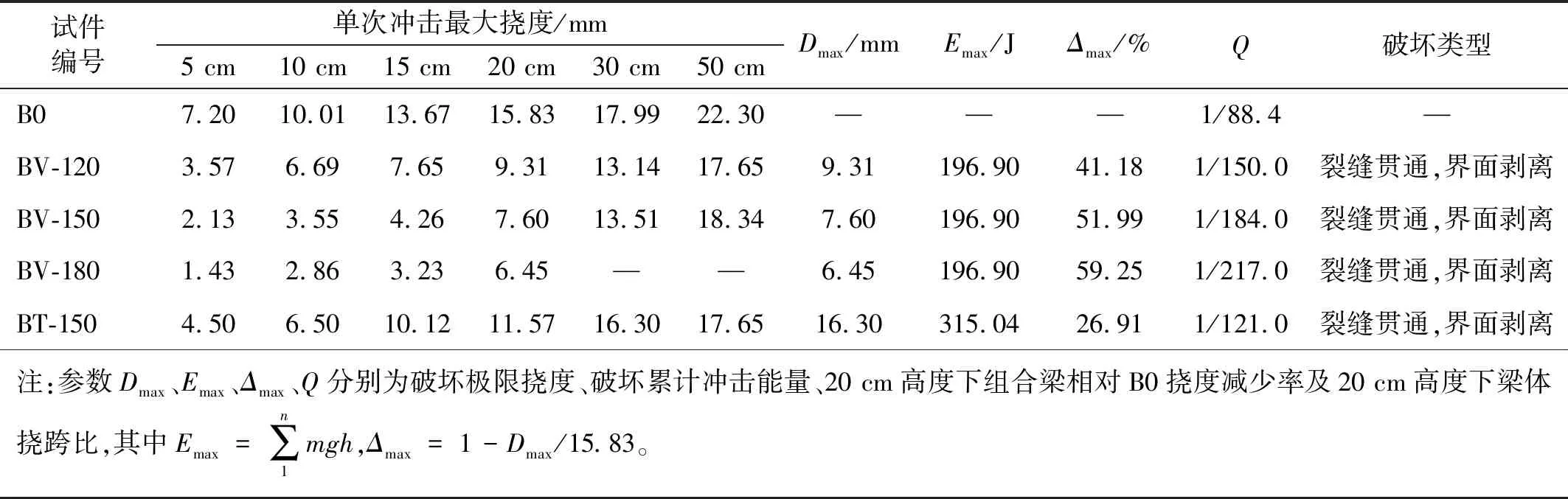
表3 试验梁挠度响应汇总

2.3 冲击力时程曲线

各试验梁在不同冲击高度下的冲击力时程曲线如图8所示。

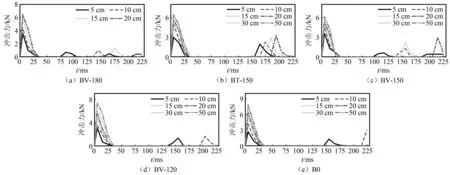
图8 试验梁冲击力时程曲线Fig.8 Time course curve of test beam impact force

所有试件的冲击力时程曲线呈现相同的规律:梁体所受冲击近似为三角形脉冲,且在一次冲击试验中受到多次锤体撞击。首次接触后冲击力快速上升,在t=5 ms左右冲击力达到首个峰值,随后冲击力迅速衰减;在t=30 ms左右时衰减到0,并维持一段时间的稳定,表明此阶段内冲击锤与梁体分离。之后锤体再次冲击梁体跨中,由于冲击锤能量在第一次冲击时被梁体大量耗散,故第二次冲击时梁体所受冲击力相对较小。对于同一试验梁,冲击高度越低,冲击锤回弹时速度越小,梁体所受到的冲击间隔时间越短;对于不同混凝土厚度的试验梁,混凝土厚度越大,梁体所受到的冲击时间间隔越短。对比裂缝开展时间可知,冲击峰值持时短,在主裂缝形成后衰减到零,此时梁体已产生不可修复的损伤,随后梁体的自身振荡进一步加剧了自身损伤。对比梁体跨中位移时程曲线来看,跨中位移峰值相较于冲击力峰值有一定的延迟,其原因是梁体在冲击荷载衰减后由于惯性作用挠度仍持续增大。

图9为试验梁冲击力峰值随冲击高度变化曲线。从图9中可知冲击峰值随冲击高度上升总体呈增大趋势,但不同混凝土厚度及冲击方式下,梁体冲击力峰值呈现较大的离散性,这主要与冲击角度、梁体刚度及二者的接触状态有关。

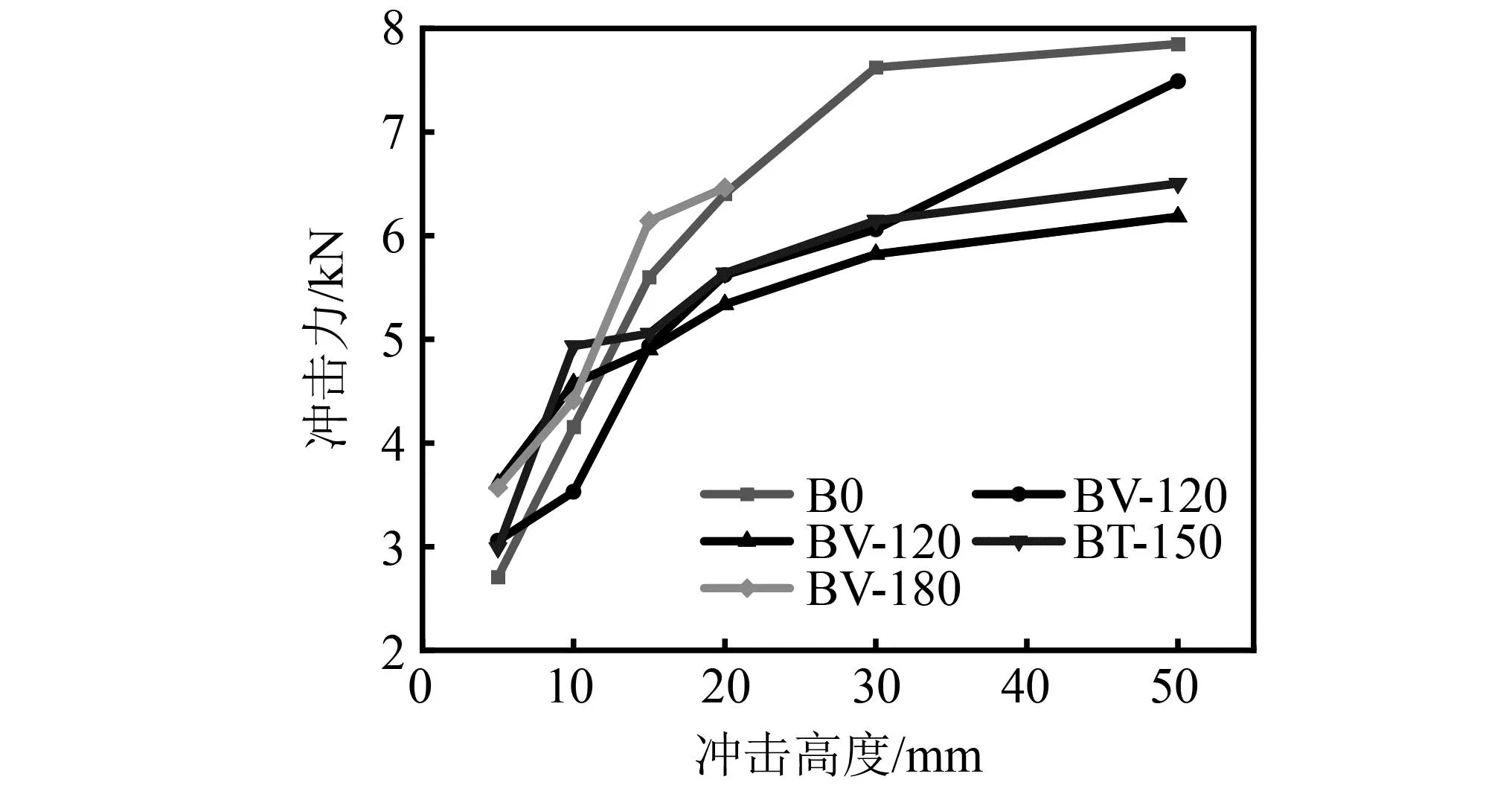
图9 试验梁冲击力峰值随冲击高度变化曲线Fig.9 Peak impact force curve of test beam with impact height

2.4 应变时程曲线

试验过程中将应变片布置于混凝土跨中顶部及FRP跨中底部,通过DASP(data acquisition &signal processing)动态采集系统以采集频率1 024 Hz测取冲击过程中材料应变发展状况。各组合梁的应变分布规律大体相同,以BV-150试验梁为例对组合梁的应变进行分析。

图10为试件BV-150在不同冲击高度下跨中应变时程曲线。从图10中可知,冲击产生的应力波在材料中传播非常迅速,混凝土最大压应变与GFRP最大拉应变发生时刻极其接近。相较于冲击力峰值,在冲击锤与组合梁首次接触后,梁体跨中应变峰值时刻有一定滞后,但与挠度峰值时刻近似相同。梁体自身震荡进一步导致混凝土与GFRP在拉压应力之间反复转换,应变数值及性质不断变化,随着梁体趋于稳定,最终在0附近上下波动。结合BV-150试验梁破坏状态来看,在冲击高度10 cm时,主裂缝得到了产生和发展,混凝土刚度降低,致使下部GFRP所受冲击力占比增大,最大拉应变得到大幅度提升(εG5=6 283.17 με,εG10=10 197.61 με,提升程度62.3%),在冲击高度20 cm时,混凝土裂缝贯通,此时混凝土极限应变约为6 427.58 με。比较混凝土及GFRP应变峰值可知,随着冲击能量的增大,GFRP应变峰值εG与混凝土应变峰值εC得到显著提高,且差值ΔC-G逐渐增大,这意味着组合梁破坏前中性轴位置不断上移,此应力分布情况对于发挥GFRP优秀的抗拉性能十分有利。(注:εG、εC分别为GFRP、混凝土峰值应变)。

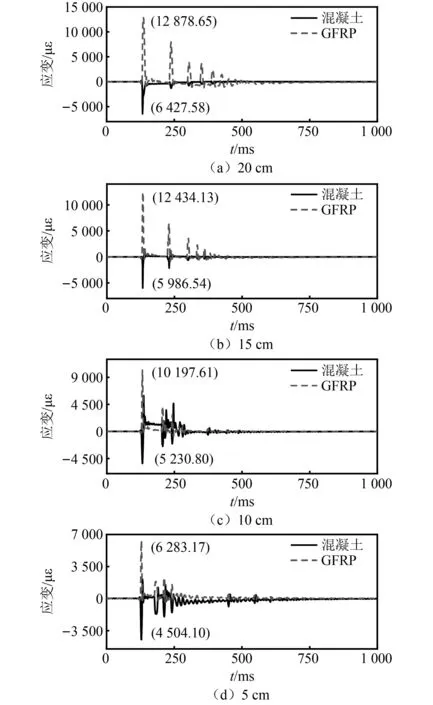
注:图10中数字为最大应变值;当冲击高度为30 cm、50 cm时,混凝土裂缝贯通,顶部应变片损坏,故不做考虑。

3 GFRP混凝土组合梁抗冲击数值模拟研究

3.1 有限元模型

使用显示动力分析软件ANSYS/LS-DYNA,以BV-120试验梁为原型,建立GFRP-混凝土组合梁累计冲击模型,材料参数如表4所示。混凝土采用非线性塑性随动强化模型(*MAT_PLASTIC_KINEMATIC),该模型利用Cowper-Symonds模型,将屈服应力与因子进行比例缩放,以此来考虑混凝土应变率的影响[26]。GFRP型材在有限元中采用正交各向异性线弹性模型(*MAT_OPTIONTROPIC_ELASTIC),由于FRP材料在高应变率下没有表现出强度增强,故不考虑应变率效应[27]。冲击锤选用刚体模型(*MAT_RIGID)。混凝土、GFRP型材,冲击锤单元类型均为八节点六面实体单元(*SOLID164),单元尺寸为10 mm。

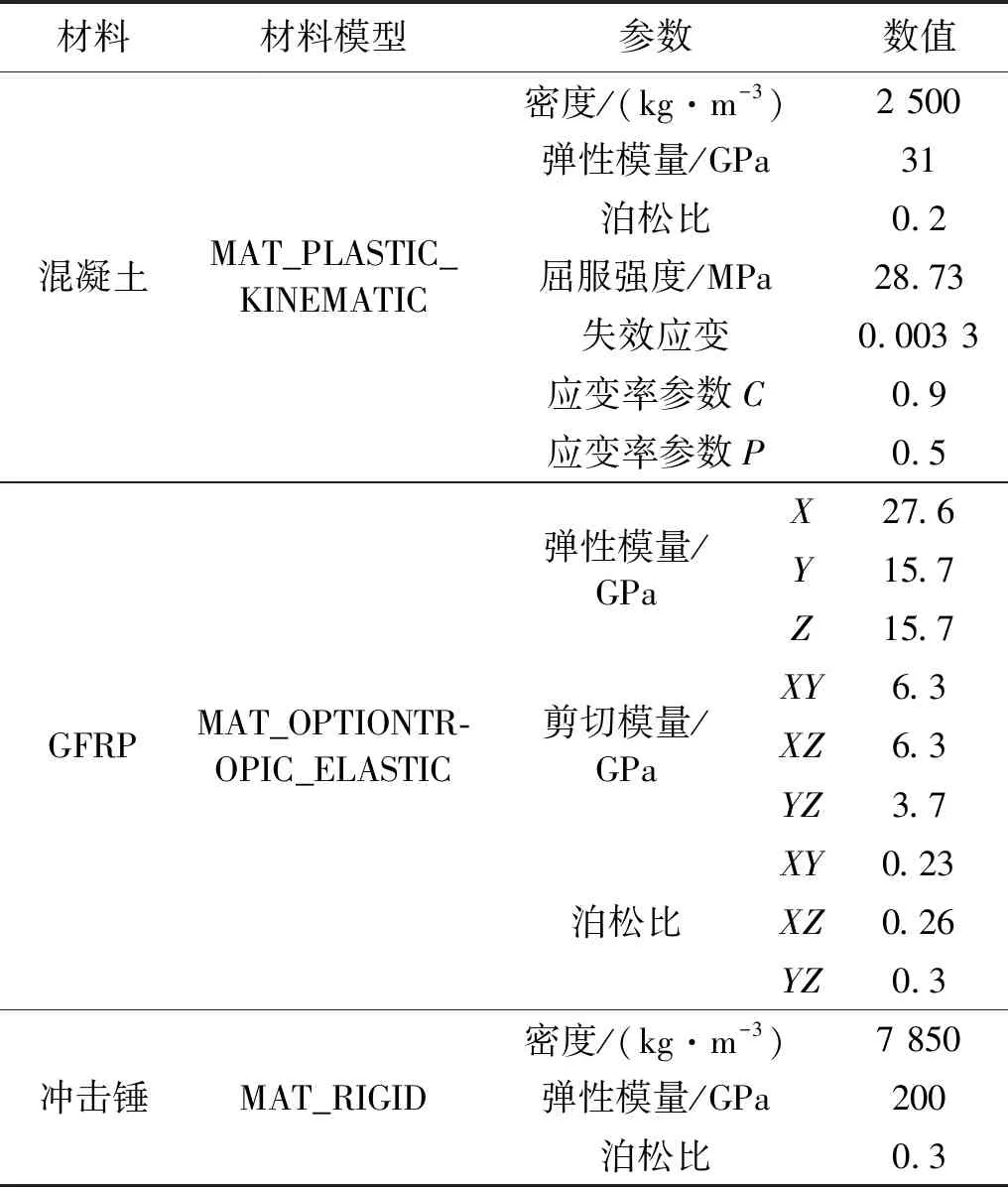
表4 有限元材料参数

在组合梁X轴向100 mm、1 500 mm处分别约束XY、YZ方向以实现简支约束,同时约束支座间(100～1 500 mm)GFRP与混凝土的侧向(Z)移动。为实现对试验梁的累次冲击,建立6个相同的冲击锤模型,冲击质量均为40.18 kg。冲击锤与混凝土的接触面积为88.5 mm×88.5 mm,并限定其只能于Y方向上运动,以确保加载方向及加载点不变。混凝土与GFRP间通过共用节点进行黏结。混凝土、GFRP型材及冲击锤间接触类型均为自动面面接触(*CONTACT_AUTOMATIC_SURFACE_TO_SURFACE)。各冲击锤之间不定义接触,以免冲击锤运动过程中彼此产生影响。计算模型如图11所示。

图11 GFRP-混凝土组合梁冲击计算模型Fig.11 Calculation model of GFRP-concrete laminated beam under impact loading

模型中的荷载主要为重力荷载,荷载的施加可以分为两部分:①模拟计算全过程中对梁体施加重力荷载;②对冲击锤分阶段施加重力荷载。重力施加流程如图12所示。

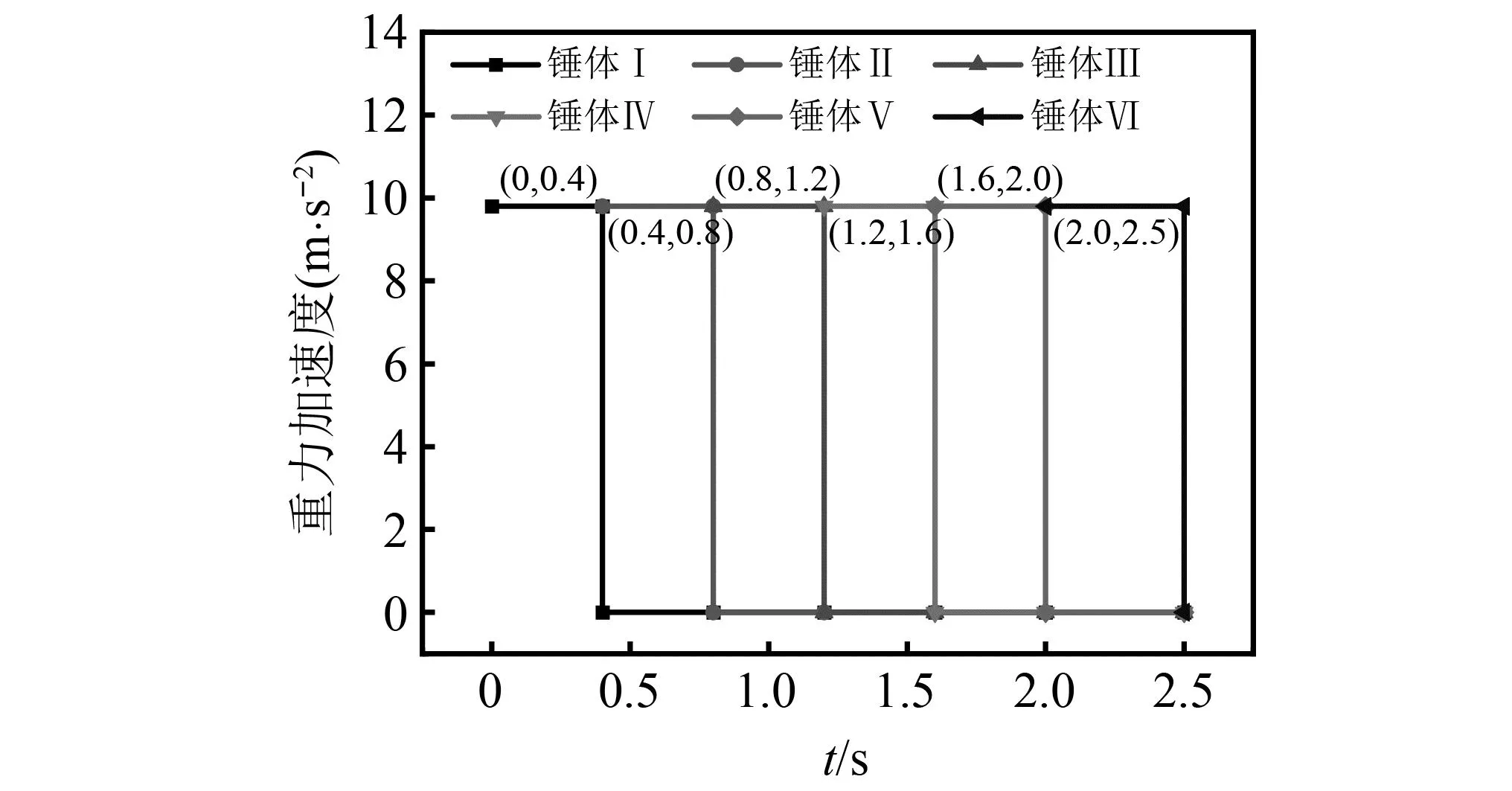
注:每次冲击前,可认为梁体已达到平衡状态;当超过设定冲击时间时,冲击锤会立即失去重力,并沿Y轴向上移动。

3.2 数值分析结果讨论

数值仿真模型得到的BV-120试验梁结构损伤过程如图13(a)所示,可发现其具有以下特征:在5 cm、10 cm冲击后,试验梁无裂缝发展及损伤;15 cm冲击后,梁体出现明显塑性损伤,跨中附近出现两条竖向裂缝,但此时并未贯通;20 cm冲击后,跨中主竖向裂缝贯通,GFRP与混凝土界面出现剥离,上部混凝土开始向两侧扩展;30 cm的冲击后,跨中混凝土出现新的裂缝,GFRP与混凝土界面出现大面积剥离;50 cm的冲击后,梁体跨中处出现严重的塑性损伤分布,混凝土大面积剥落,构件完全破坏。通过与BV-120试验梁试验损伤过程(图13(b))比较可知,不论是裂缝发展特征,或是构件各冲击高度下损伤分布,数值仿真结果均与实际相符,说明利用LS-DYNA建立的GFRP-混凝土组合梁累计冲击模型能够较为准确反应BV-120试验梁在冲击过程中的裂缝发展及损伤状况。

图13 BV-120试件冲击试验及数值模拟破坏过程Fig.13 BV-120 specimen failure process of impact test and numerical simulation

图14给出了采用有限元模型计算得到的BV-120梁在不同冲击高度下的跨中挠度最大值,对比BV-120试验中各冲击高度下的跨中最大挠度值可发现,数值模拟结果同试验结果非常接近。不同冲击高度下,试验与数值模拟跨中挠度峰值误差率|R|多为在10%左右,且15 cm冲击和50 cm冲击时跨中挠度峰值的误差率|R|仅为2.9%和3.5%。这表明本文所建立的GFRP-混凝土组合梁累计冲击计算模型能够较好地反映试验梁在冲击荷载过程中的挠度响应。

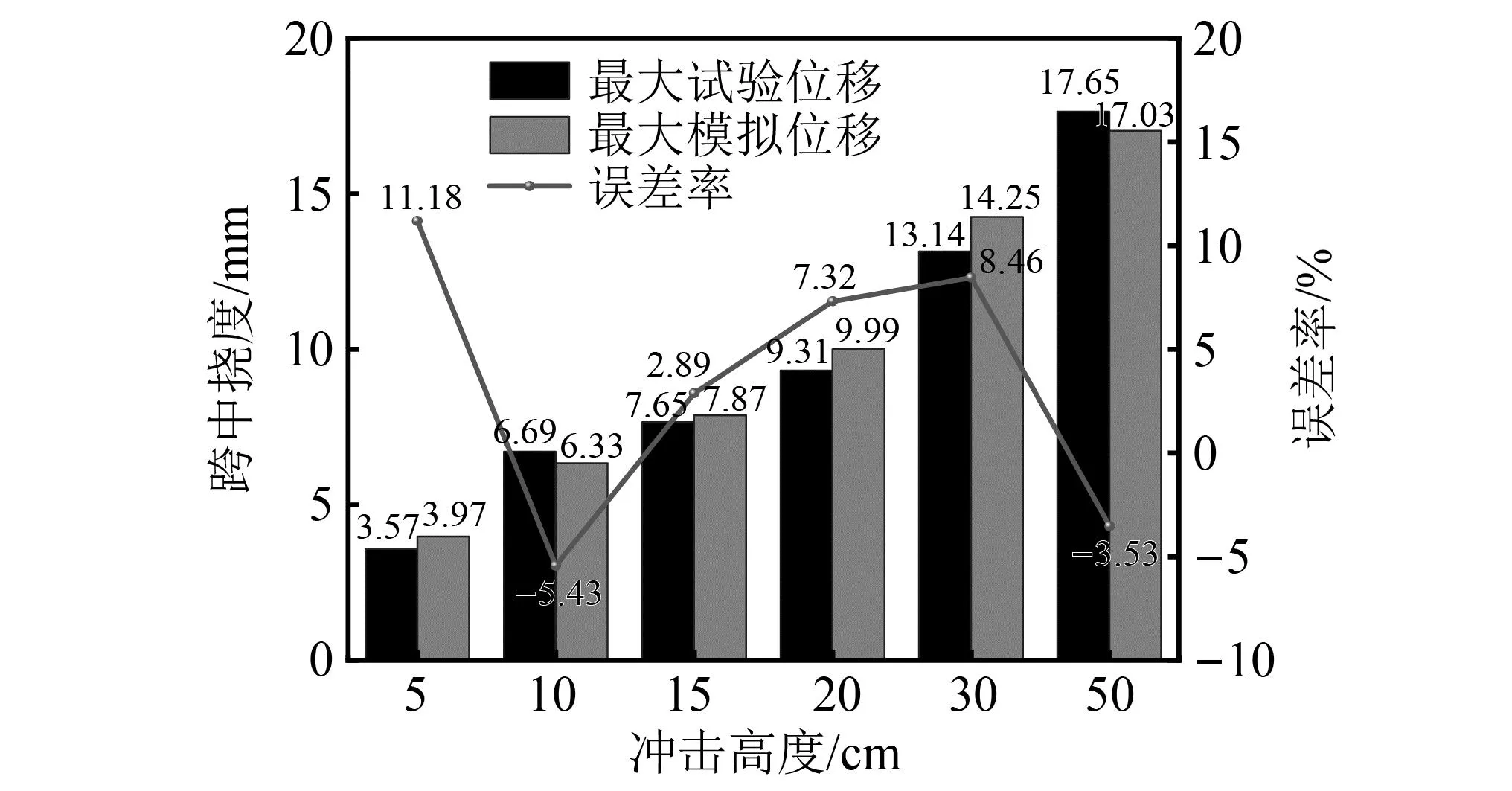
注:误差率R=[模拟值S-试验值T)/试验值T]×100%。

图15为BV-120试验梁破坏前不同冲击高度下数值模拟与试验冲击力峰值对比图。从图15中可知,虽然数值模拟计算得到的冲击力峰值均高于试验过程中得到的冲击力峰值,但考虑到试验误差,且在冲击高度为5 cm、15 cm、20 cm时,数值模拟与试验冲击力峰值误差率|R|(计算公式同挠度峰值误差率)均在10%附近,可认为采用LS-DYNA建立的GFRP混凝土组合梁累计冲击计算模型可以较为准确地模拟出梁体所受的冲击荷载。

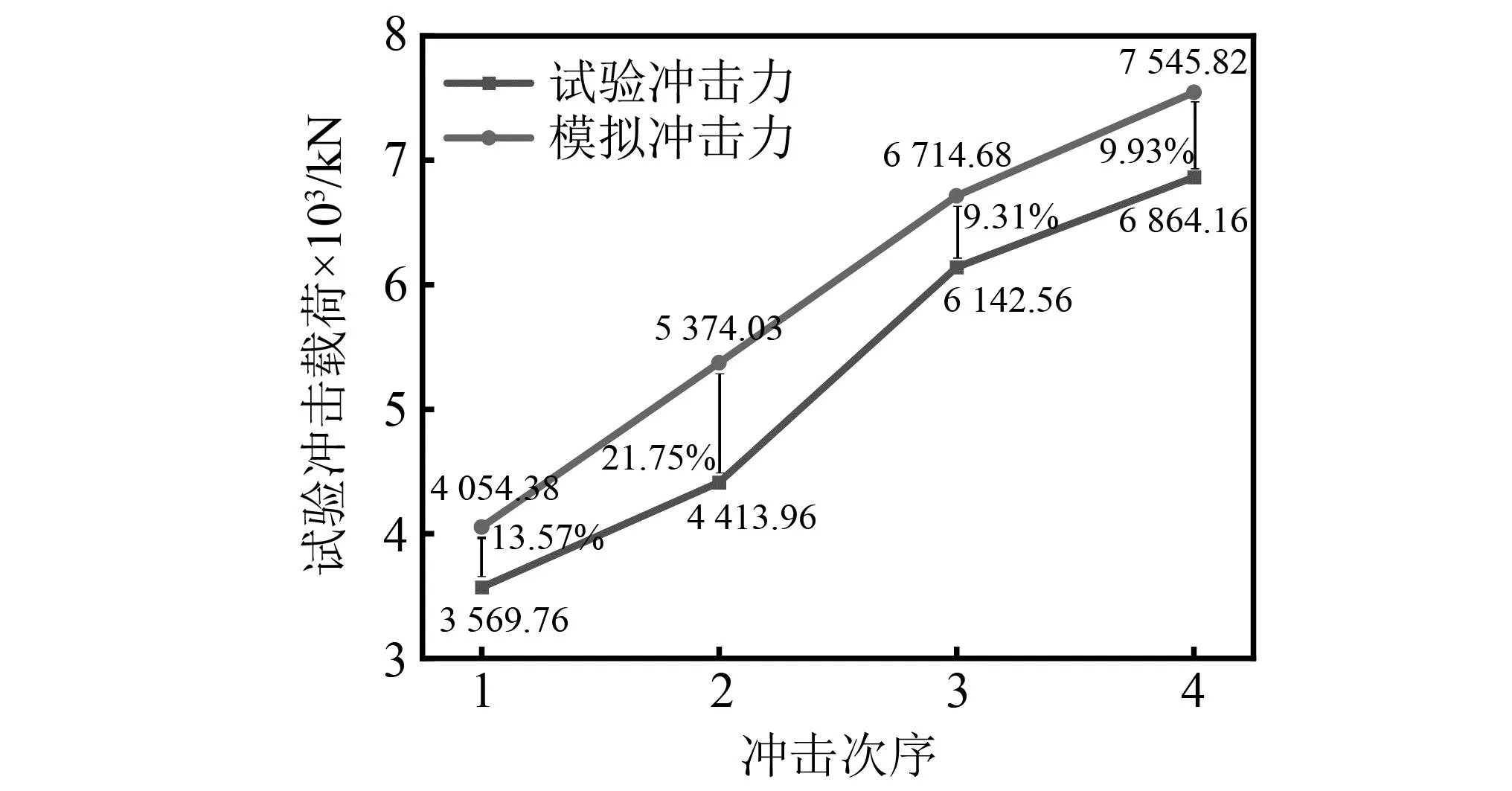
图15 BV-120模拟及试验冲击力结果对比Fig.15 BV-120 simulation and test impact force results comparison

综合对比BV-120试验与有限元模型中裂缝发展状况、结构损伤分布、跨中挠度及冲击力结果可知,本文建立的GFRP-混凝土组合梁累计冲击计算模型能够较好地反应组合梁的动力冲击响应。

4 GFRP-混凝土组合梁冲击响应影响参数分析

4.1 冲击物质量

冲击物质量是影响构件冲击响应的重要参数,在山区落石冲击事件中,冲击物质量往往很大,为研究冲击物质量对GFRP-混凝土组合梁冲击响应的影响,在GFRP-混凝土组合梁结构尺寸(图16(a))和冲击速度(5 m/s)保持不变的前提下,通过有限元模型(图16(b))模拟了冲击物质量为10 kg、50 kg、100kg、300 kg、500 kg、700 kg和1 000 kg情况下GFRP-混凝土组合梁的动态响应(见图17(a),表5)。

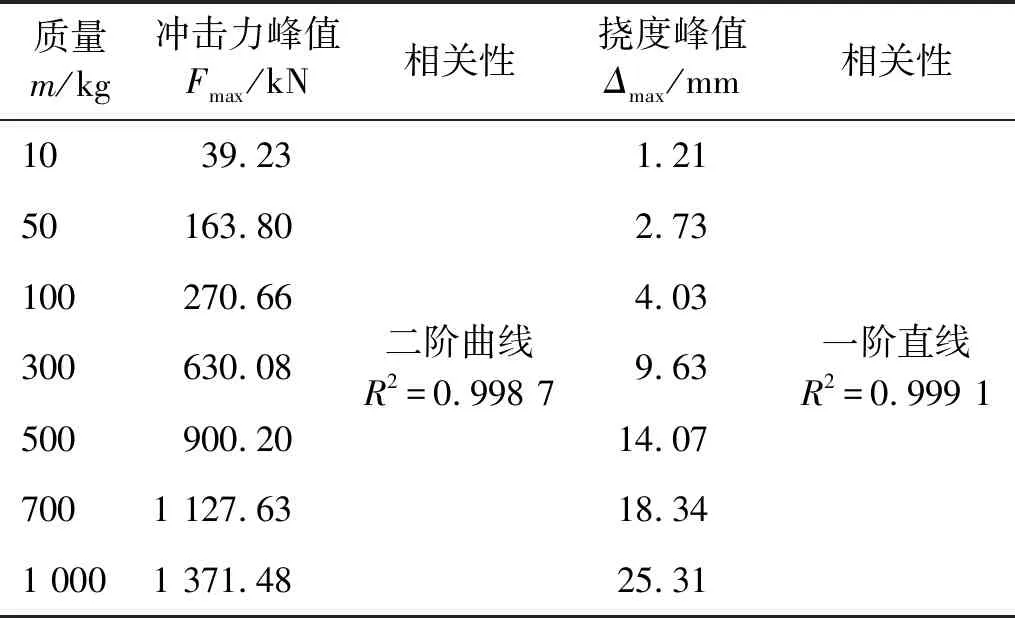
表5 不同冲击物质量下梁体动态响应峰值

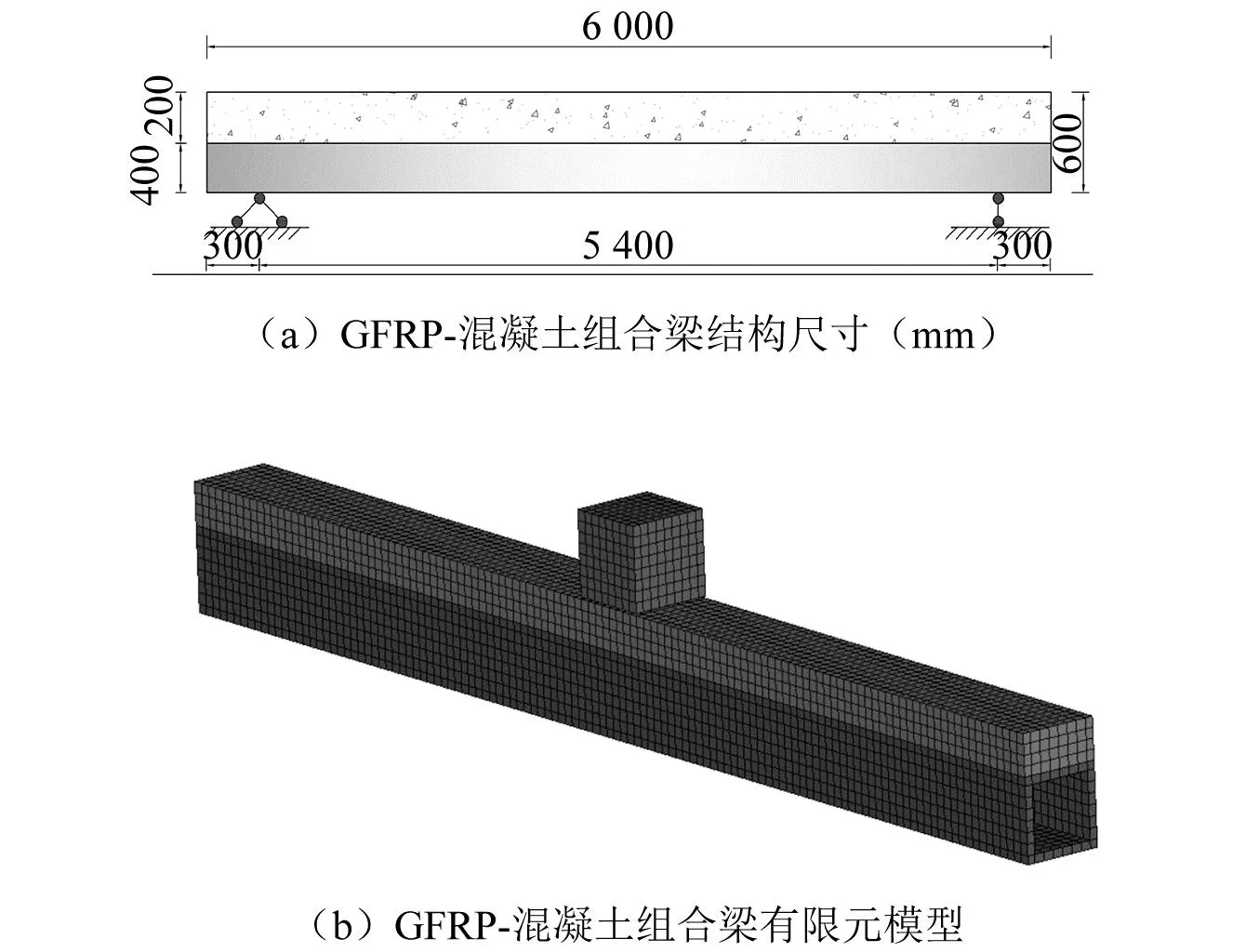
图16 GFRP-混凝土组合梁结构尺寸及有限元模型Fig.16 Structural dimensions and finite element model of GFRP concrete composite beam

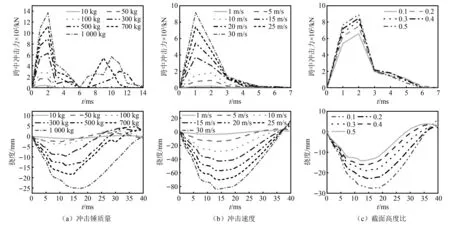
注:图17中,上边图为梁体跨中冲击力时程曲线,下边图为梁体跨中挠度时程曲线。

从组合梁冲击力时程曲线可知,随着冲击锤质量增大,冲击力峰值明显增大,且冲击持时有一定程度延长。在10～500 kg冲击物质量下,冲击力时程曲线表现为“单峰型”,而在700～1 000 kg冲击物质量下,冲击力时程曲线表现为“双峰型”。原因为随着冲击物质量增大,锤体和梁体之间更趋向于完全非弹性碰撞,冲击物在冲击过程中会损失更多动量。当冲击物与梁体分离时刻,质量大的冲击物速度小于质量小的冲击物速度,并在自质量的作用下迅速下落,与混凝土产生二次碰撞,由此产生“第二个峰值”。观察组合梁挠度时程曲线可知,不同冲击物质量下,组合梁跨中挠度变化趋势相同。随着冲击质量的增大,峰值挠度也相应增大;同时,冲击物与梁体接触时的瞬间速度增大,构件需花费更多变形时间来消耗冲击能量,即挠度峰值点时刻延后。利用多项式曲线对组合梁冲击力峰值、跨中挠度峰值与冲击物质量关系进行拟合,得到冲击力峰值与冲击物质量满足上凸二阶曲线关系,跨中挠度峰值与冲击物质量满足一阶线性关系(见图18(a))。冲击物质量增加,组合梁冲击力峰值增速减缓,但跨中位移峰值仍保持一定的线性增加。因此,在组合梁设计时,应充分考虑大质量冲击导致结构产生大挠度的工况,通过合理的截面设计与材料类型选择,减少大质量冲击下构件的变形响应。

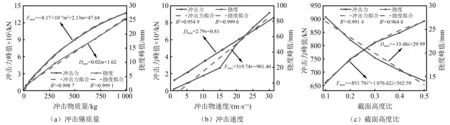
注:拟合函数中,m、v、λ分别为冲击物质量、冲击物速度、截面高度比。

4.2 冲击速度

为研究冲击速度对GFRP-混凝土组合梁冲击响应的影响规律,保持组合梁结构尺寸及冲击质量(500 kg)不变,对冲击速度为1 m/s、5 m/s、10 m/s、15 m/s、20 m/s、25 m/s和30 m/s工况下梁体冲击响应进行了分析(见图17(b),表6)。

从组合梁冲击力时程曲线可知,不同冲击速度下组合梁冲击力时程曲线的趋势基本一致,冲击力作用时间约6 ms。组合梁冲击力峰值随冲击速度的增加而增加,增幅稳定。观察组合梁挠度时程曲线可知,冲击速度增大,跨中挠度峰值也相应增大,但跨中挠度峰值出现时刻逐渐延后。利用多项式函数对组合梁冲击力峰值、跨中挠度峰值与冲击速度关系进行拟合,可知冲击速度对组合梁冲击力峰值及跨中挠度峰值的影响均呈线性(见图18(b))。

4.3 截面高度比

截面高度比(混凝土与GFRP高度比)是影响GFRP-混凝土组合梁冲击响应的重要因素。在冲击质量(500 kg),冲击速度(5 m/s)不变的前提下,研究了构件截面高度比为0.1、0.2、0.3、0.4和0.5的工况下组合梁动态响应。通过调节冲击高度,统计了各工况下混凝土首次产生贯穿裂缝,即组合梁发生破坏时的耗散能量(见图17(c)及表7)。观察梁体冲击力时程曲线可知,结构的冲击力峰值随着截面高度比地增加而增加,但增幅逐渐减小。观察跨中挠度时程曲线可得,构件的跨中挠度峰值随着截面高度比地增加而减小,降幅稳定。利用多项式函数对冲击力峰值、跨中挠度峰值与截面高度比关系进行拟合,得到冲击力峰值与截面高度比间满足二阶曲线关系,跨中挠度峰值与截面高度比满足线性关系(见图18(c))。

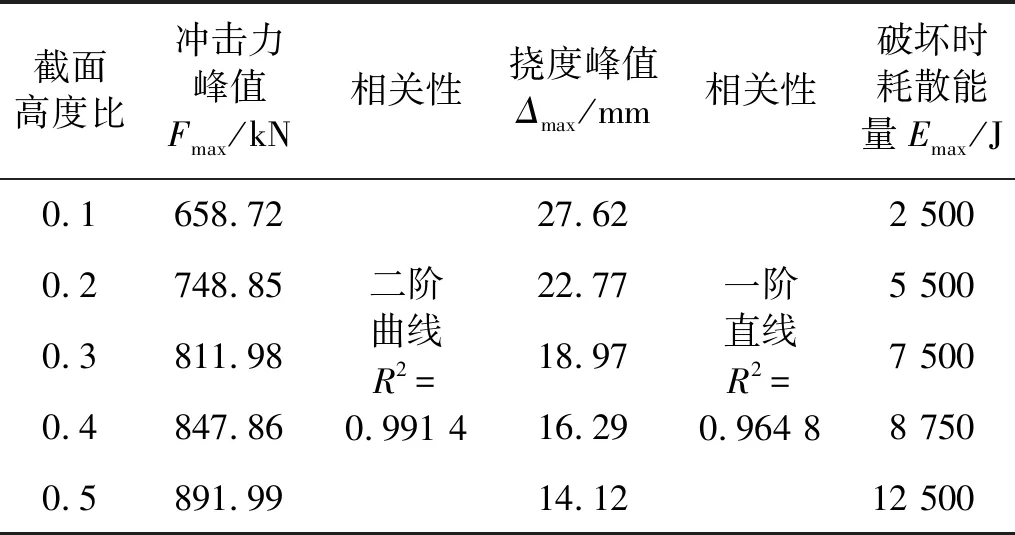
表7 不同截面高度比下梁体动态响应峰值

对梁体动态响应峰值进行无量纲化处理(见图19)。综合考虑构冲击力峰值、挠度峰值及耗散能量,当截面高度比为0.3～0.5时组合梁冲击力峰值增长较缓且跨中挠度峰值较小,并具有良好的耗散冲击能量的能力。在实际应用过程中,需保证组合梁中性轴位于GFRP上,利用弹性分析换算截面法求得此构件的截面高度比应小于0.375。由此可知,GFRP-混凝土组合梁截面高度比的合理取值范围为0.300～0.375。

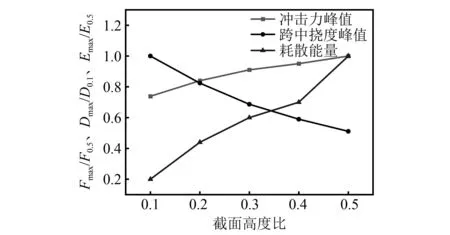
图19 冲击力峰值、跨中挠度峰值、耗散能量值随截面高度比变化的曲线Fig.19 Curves of peak impact force, peak mid-span deflection,and dissipated energy values with section height ratio

换算截面法计算步骤如下。GFRP-混凝土组合梁横截面参数如表8所示。

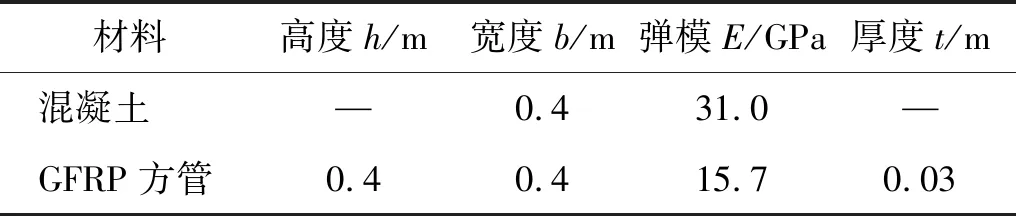
表8 GFRP-混凝土组合梁横截面参数

在组合梁截面的弹性分析中,采用如下假设:①GFRP和混凝土材料均为理想的线弹性体;②GFRP与混凝土翼板之间连接可靠,滑移可以忽略不计,符合平截面变形假定;③有效宽度范围内的混凝土翼板按实际面积计算,不扣除其中受拉开裂的部分。

首先根据合力不变及应变相同条件,把混凝土换算成GFRP材料。

弹性模量比

EC/EG=1/αG

(1)

等价的换算截面面积

AG2=ACEC/EG

(2)

为保证组合截面形心高度即合力位置换算前后保持不变,换算时固定混凝土厚度而只改变其宽度,如图20所示。

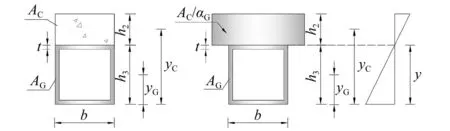
图20 组合梁换算前后横截面Fig.20 Cross section of the combined beam before and after conversion

中性轴位置

y=(AGyG+AG2yC)/(AG+AG2)

(3)

当y≥h3时,求解可得

h2/h3≤0.375

(4)

式中:EC、EG分别为混凝土、GFRP弹性模量;AC、AG分别为横截面混凝土、GFRP面积;AC=bh2、AG=2bh3+2(b-2t)h3;yC、yG分别为横截面混凝土、GFRP中心位置。

5 结 论

本文采用摇臂式落锤冲击试验系统对纯GFRP梁及GFRP-混凝土组合梁进行了累计冲击试验,获取了多次落石冲击荷载下试验梁的动态响应数据,深入分析了冲击过程中组合梁损伤分布及动态响应特征,基于显式有限元分析方法对GFRP-混凝土组合梁累计冲击过程进行了仿真及影响因素分析。研究结果表明:

(1)本试验中,纯GFRP试件在竖向冲击荷载下无明显损伤及塑性变形,表明GFRP试件具有良好的抗冲击性能,但易产生较大变形。混凝土高度地增加,组合梁刚度增大,同时在应力波地传播、衰减及反射过程中,混凝土吸收的冲击能量增多,GFRP受到的冲击能量降低,进而组合梁的变形响应减小。

(2)竖向冲击荷载下,不同混凝土厚度的GFRP-混凝土试验梁破坏高度均为20 cm,其破坏过程可分为弹性阶段、裂缝产生、发展及主裂缝贯通4个阶段,最终破坏特征均为混凝土主裂缝贯通,GFRP与混凝土发生剥离,二者良好的黏结能力对GFRP-混凝土组合梁抗冲击性能至关重要。

(3)侧向冲击和竖向冲击相比,在主裂缝贯通前,试验梁抵抗侧向冲击性能优于其抗竖向冲击,但试验梁受侧向冲击时变形较大。

(4)综合对比试验与有限元法组合梁裂缝发展状况、结构损伤分布、跨中挠度及冲击力试验结果,可知通过分阶段施加重力荷载能够较为准确地模拟GFRP-混凝土试验梁在累计冲击过程的结构损伤与动态响应。

(5)在GFRP-混凝土组合梁的弯曲破坏条件下,当冲击物质量、速度等非构件因素及截面挠度比等构件因素发生变化时,梁体所受冲击力峰值和跨中挠度峰值呈现二阶曲线或线性变化趋势。进行组合梁设计时,混凝土与GFRP最优的高度比为0.300～0.375,并应充分考虑结构面临大质量冲击时的工况。