中低速磁浮最小曲线半径及缓和曲线长度研究

林远扬, 李 苗, 马卫华, 王 波, 张 敏, 左飞飞

(西南交通大学 轨道交通运载系统全国重点实验室,成都 610031)

21世纪以来,我国在高速铁路、重载铁路、城市轨道交通和磁浮交通四大领域发展迅猛,取得了举世瞩目的重大成就[1]。日益完善的轨道交通网络,为旅客出行带来极大便利的同时,也进一步激发了人们的期望[2]。其中,中低速磁浮交通摆脱了传统轮轨黏着的限制,且具有转弯半径小、爬坡能力好、选线适应性强等优点,受到许多国家的广泛关注和持续研究[3]。线路参数作为中低速磁浮交通最基本的设计参数,其取值大小对于中低速磁浮交通的列车运行品质和建设成本具有重要影响。因此,科学合理地设计中低速磁浮交通的线路参数,是推动中低速磁浮交通发展中面临的问题之一。

曲线半径大小、缓和曲线长度是线路设计的关键参数,其在保证车辆运行效率的同时,还需要保证车辆具有优秀的乘坐舒适度,因此其研究受到国内外众多学者的关注。在磁浮车辆的曲线半径研究中,王相平等[4-5]通过仿真研究了小半径曲线上的磁浮车辆-轨道耦合系统振动特性,得到车体、空气弹簧等部件的动力响应。姚金斌等[6-7]从乘客舒适度、磁浮列车技术要求等方面对中低速磁浮线路最大横坡角取值进行了分析,进而给出最小平曲线半径取值。时瑾等[8]通过计算中低速磁浮车辆滑枕偏移距离、弹簧变形量等指标,对其最小平、竖曲线半径展开了研究,并提出建议值。Jiang等[9]基于理论分析得到高速磁浮最小平曲线半径理论值,并通过动力学仿真对其优化调整。在磁浮车辆的缓和曲线研究中,武巍[10]通过仿真研究了缓和曲线参数对中低速磁浮动力学性能的影响规律,得到了乘客舒适度随缓和曲线类型及长度的变化关系。米隆等[11-12]基于行驶动力学理论,推导出适用于高速磁浮线路的平、竖缓和曲线长度计算公式,进一步提出其建议值。苟智平[13]参照高速轮轨铁路线路参数的设计方法,对高速磁浮线路平面缓和曲线展开了研究,并得到一系列取值。Han等[14]利用建立的中低速磁浮列车模型分析了缓和曲线参数对列车悬浮稳定性的影响,得到悬浮稳定性随缓和曲线参数的变化规律。

上述研究成果一定程度上促进了磁浮交通的选线设计,但目前中低速磁浮线路研究成果均为基于速度在100 km/h等级以下曲线半径取值的研究,且多数研究仅通过受力分析得到最小曲线半径取值,该方法将车辆视为质点,未考虑车辆中各部件之间的相对运动关系;对于缓和曲线的研究,则多集中在高速磁浮线路缓和曲线的取值,且上述研究均忽略了列车在缓和曲线上运行时受到的法向冲击为空间曲线决定的法向冲击和横坡扭转产生的法向冲击的叠加。而中低速磁浮列车运行速度得到提升、系统结构复杂且线路缓和曲线类型不同于高速磁浮线路的一波正弦型,因此有必要开展中低速磁浮线路最小曲线半径及缓和曲线长度的研究。

1 舒适度控制目标值

旅客舒适度是指列车运行时,车上旅客受到车体各种运动的作用后,在生理和心理上感觉不舒适的程度。由于中低速磁浮列车多采用“抱轨”的方式运行,降低了列车脱轨的风险。因此,旅客舒适度控制目标值是中低速磁浮列车线路参数选取的主要影响因素。列车行驶过程中会产生振动,在通过曲线路段时,车体会产生未被平衡的侧向、法向离心加速度,当产生的离心加速度为0时,线路的曲率、横坡角和列车的运行速度必须完美匹配,这较难实现。因此,CJJ/T 262—2017《中低速磁浮交通设计规范》[15]、TB 10630—2019《磁浮铁路技术标准(试行)》[16]规定了其最大允许值来保证旅客乘坐的舒适度,各舒适度控制目标值如表1所示。

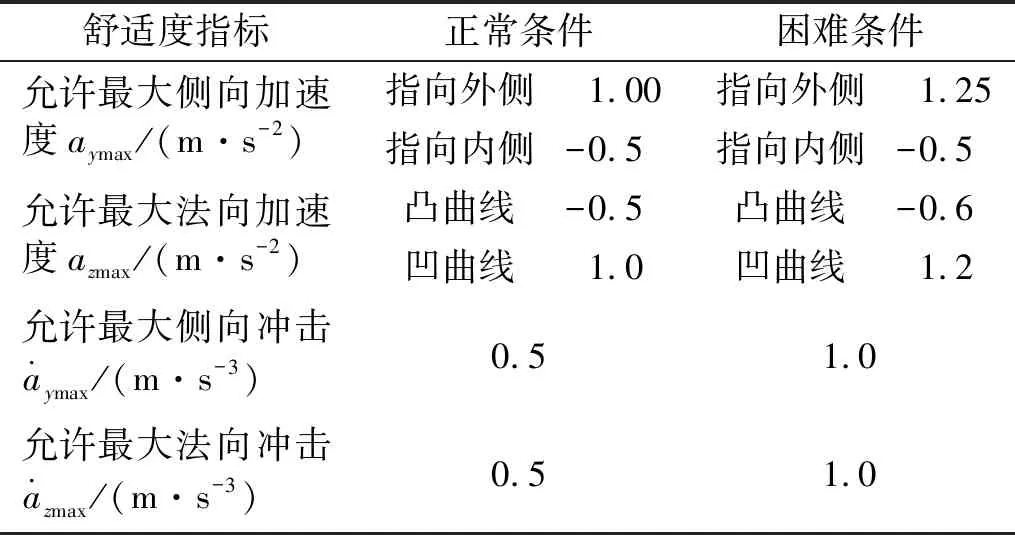
表1 舒适度控制目标值Tab.1 Comfort controls the target value

2 最小曲线半径

曲线半径是磁浮线路的关键参数之一,最小曲线半径是指在规定的横坡角、纵坡、行车速度等条件下,既保证列车在曲线路段时,产生的离心力等横向力不超过轨道与车辆之间阻力所允许的限值,又能使车上旅客感觉舒适的临界半径。根据曲线线路相邻两坡段纵坡是否为0,曲线半径可分为平曲线半径和竖曲线半径。

2.1 最小平曲线半径

中低速磁浮列车通过空间曲线时的受力情况如图1所示。图1中:Y轴、Z轴分别平行、垂直于轨面;α、β分别为横坡角、线路中心线的纵坡角;Re为空间圆曲线的半径;m为中低速磁浮列车质量;g为重力加速度,取9.81 m/s2;FN为轨道对磁浮列车的反作用力;ay、az分别为磁浮列车在曲线上运行时受到的未平衡离心侧向、法向加速度;FH、FV分别为磁浮列车通过平曲线、竖曲线时受到的离心力,FH、FV的计算公式为

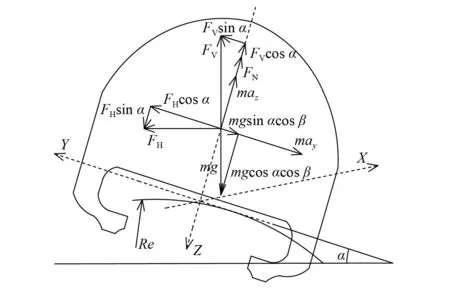
图1 中低速磁浮列车通过空间曲线时的受力情况Fig.1 The force on a medium- and low-speed maglev train as it passes through a spatial curve

(1)

(2)

式中:V为磁浮列车运行速度;RH和RV分别为平曲线和竖曲线半径。

当列车通过曲线时,在Y轴方向的受力应满足

may≥FVsinα+FHcosα-mgsinαcosβ

(3)

将FH、FV代入式(3)得到平曲线半径计算公式

(4)

根据式(4)可见,中低速磁浮列车平曲线半径的取值受列车运行速度、横坡角、纵坡角、竖曲线半径和侧向加速度共同控制。当列车在平曲线上运行时,竖曲线半径对平曲线半径取值的影响可忽略,即RV取∞。图2为横坡角6°、侧向加速度-0.5 m/s2和1.0 m/s2时,纵坡对平曲线半径的影响。由图2可以看出,当列车运行条件、速度相同时,随着纵坡坡度的增大,平曲线半径基本保持不变,因此可忽略纵坡对平曲线半径取值的影响,即纵坡取0‰。将式(4)进一步简化为式(5)

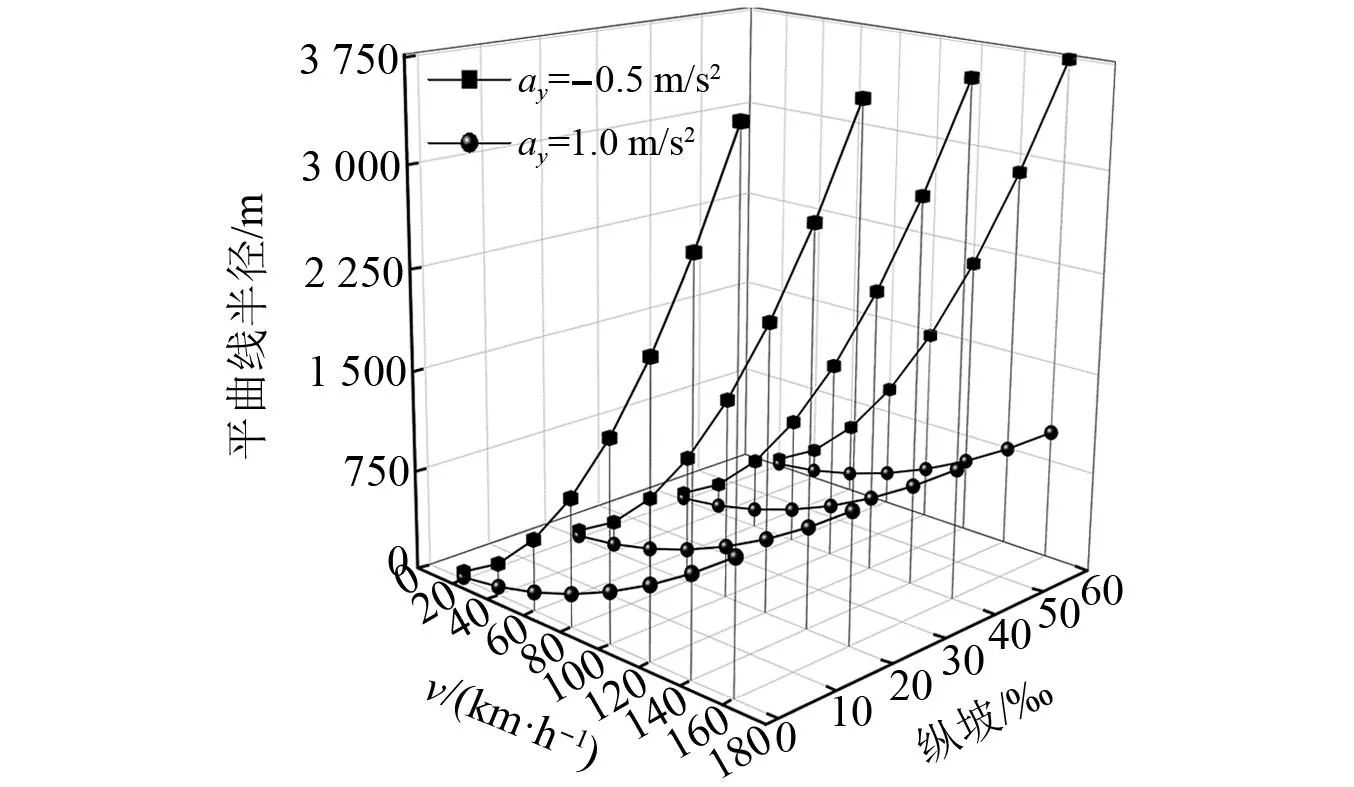
图2 纵坡对平曲线半径的影响Fig.2 Influence of longitudinal slope on radius of horizontal curve

(5)

根据CJJ/T 262—2017《中低速磁浮交通设计规范》的规定,中低速磁浮交通线路允许设置的最大横坡角为6°。因此,考虑横坡角为2°、4°、6°时,对中低速磁浮列车以20～160 km/h速度时的最小平曲线半径展开计算。其中正常条件下,aymax取-0.5 m/s2、1.0 m/s2;困难条件下,aymax取-0.5 m/s2、1.25 m/s2,对正常和困难条件下各自对应的两组计算结果进行比较,并取最小值,得到满足舒适度要求的中低速磁浮列车最小平曲线半径取值,如附录A中表A.1所示。图3为侧向加速度控制下,速度、横坡角与平曲线半径的关系,由图3可以发现,正常条件、困难条件下,指向内侧的最大侧向加速度确定的平曲线半径取值远大于指向外侧的最大侧向加速度确定的平曲线半径取值,因此指向外侧的最大侧向加速度控制着最小平曲线半径的取值;当列车通过平曲线速度一定时,横坡角越大,中低速磁浮列车可允许通过的平曲线半径越小。

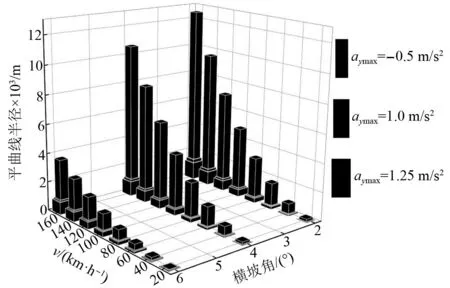
图3 侧向加速度控制下速度、横坡角与平曲线半径的关系Fig.3 Relationship between speed, cross slope angle and radiusof horizontal curve under lateral acceleration control

2.2 最小竖曲线半径

当列车通过曲线时,在Z轴方向的受力应满足

maz≥mgcosαcosβ+FHsinα-FVcosα-FN

(6)

其中,

FN≈mg

(7)

将FH、FV代入式(6)得到中低速磁浮竖曲线半径计算公式

(8)

根据式(8)可见,中低速磁浮列车竖曲线半径的取值受列车运行速度、横坡角、纵坡角、平曲线半径和法向加速度共同控制。当磁浮列车在竖曲线上运行时,平曲线半径对竖曲线半径取值的影响可忽略,即RH取∞。图4为纵坡60‰、法向加速度-0.5 m/s2和1 m/s2时,横坡角对竖曲线半径的影响。由图4可以看出,当磁浮列车运行条件、速度相同时,横坡角对线路竖曲线半径影响很小,可忽略,即横坡角取0°。因此,将式(8)进一步简化为式(9)

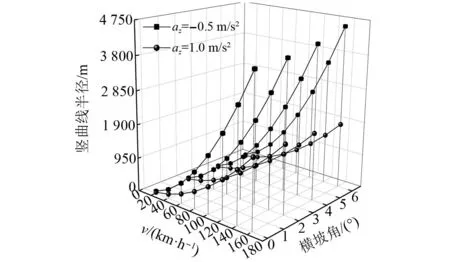
图4 横坡角对竖曲线半径的影响Fig.4 Influence of cross slope angle on radius of vertical curve

(9)

根据CJJ/T 262—2017《中低速磁浮交通设计规范》的规定,中低速磁浮交通正线的最大纵坡不宜大于60‰。因此,考虑纵坡为20‰、40‰、60‰时,对中低速磁浮列车以20～160 km/h速度通过曲线时的最小竖曲线半径展开计算。其中正常条件下,azmax取-0.5 m/s2(指向内侧)、1.0 m/s2(指向外侧);困难条件下,azmax取-0.6 m/s2、1.2 m/s2,对正常和困难条件下各自对应的两组计算结果进行比较,并取最小值,得到满足舒适度要求的中低速磁浮列车最小竖曲线半径取值,如附录A表A.2所示。图5为法向加速度控制下,速度、纵坡与竖曲线半径的关系。由图5可以发现,凸曲线上法向加速度确定的竖曲线半径取值远大于凹曲线上法向加速度确定的竖曲线半径取值,因此凹曲线上允许的最大法向加速度控制着最小竖曲线半径的取值;在中低速磁浮交通正线规定的最大纵坡范围内,纵坡对最小竖曲线半径的取值几乎无影响。

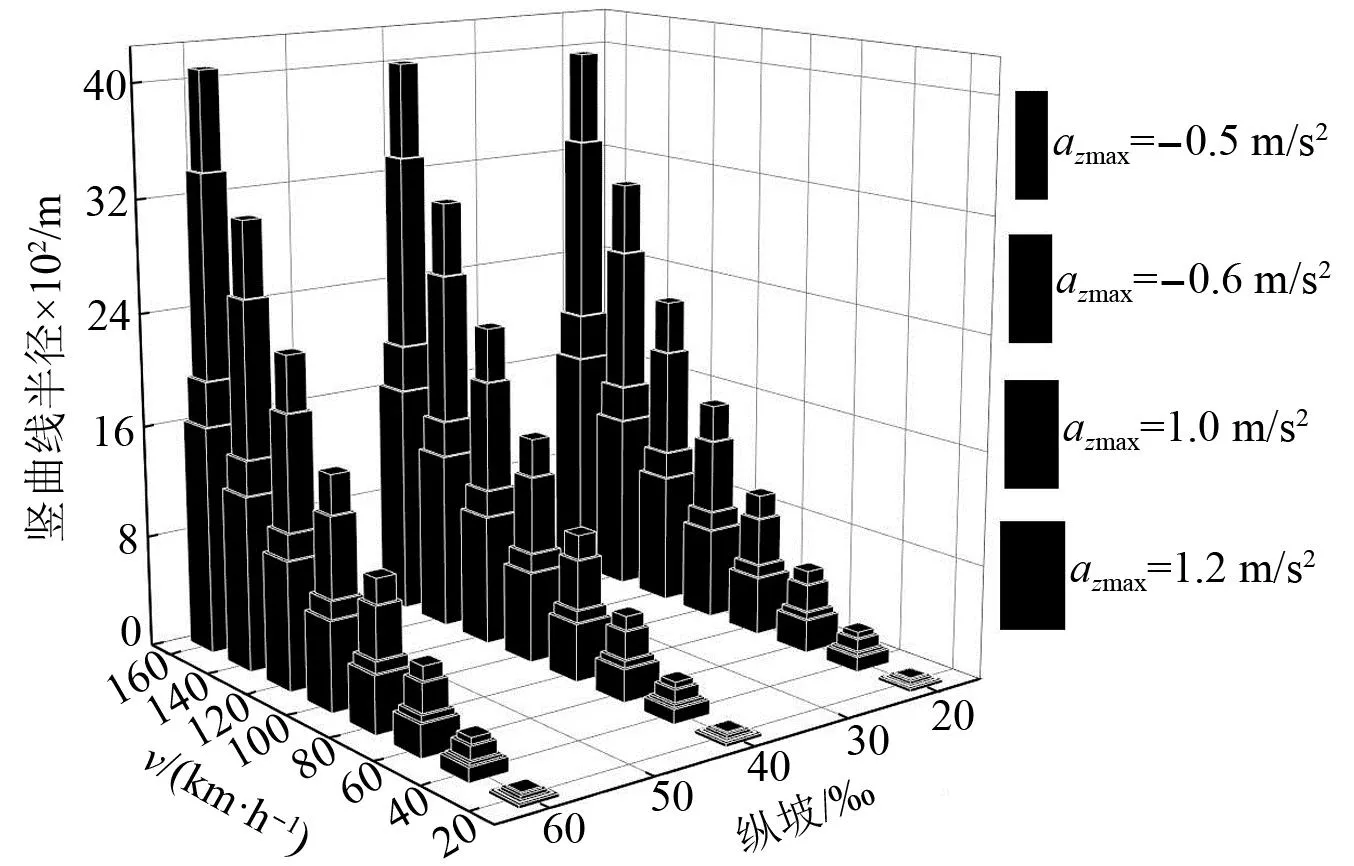
图5 法向加速度控制下速度、纵坡与竖曲线半径的关系Fig.5 Relationship between speed, longitudinal slope and radius of vertical curve under normal acceleration control

3 最小缓和曲线长度

缓和曲线是磁浮线路线形要素之一,在中低速磁浮线路纵断面设计中,在相邻两坡度之间,一般不设置缓和曲线,故中低速磁浮交通缓和曲线为平面缓和曲线,它通常用于连接圆曲线和直线或两个转向相同且半径差值较大的两段圆曲线。为了使列车能够在线路上平稳、安全地运行,国内外学者提出了很多类型的缓和曲线[17-18],如:三次抛物线型、五次曲线型、S曲线型、一波正弦型等。根据TB 10630—2019《磁浮铁路技术标准(试行)》的规定,中低速磁浮交通线路采用三次抛物线型缓和曲线,其上任意一点处的曲率和横坡角可表示为

(10)

(11)

式中:k0为圆曲线曲率;α0为圆曲线横坡角;l为缓和曲线上任意一点到直缓点的曲线距离,0≤l≤ls,ls为缓和曲线长度。

3.1 侧向冲击确定的缓和曲线长度

当中低速磁浮列车在缓和曲线上运行时,其受到的侧向加速度为

(12)

由于中低速磁浮交通线路横坡角很小,不大于6°,因此,可将式(12)进一步简化为式(13)

(13)

式中,ρ为角度制到弧度制的换算符。

若列车以匀速通过缓和曲线,则其受到的侧向冲击为

(14)

故满足侧向冲击要求的最小平面缓和曲线长度为

(15)

3.2 法向冲击确定的缓和曲线长度

当中低速磁浮列车在缓和曲线上运行时,可忽略竖曲线半径、纵坡的影响,即RV=∞,β=0‰。同时考虑外轨超高角甚小,可得列车在缓和曲线上运行时受到的由曲线决定的法向加速度

(16)

若列车以匀速通过缓和曲线,则其受到的由曲线决定的法向冲击为

(17)

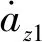
(18)

由横坡扭转产生的法向加速度应按式(19)计算

(19)

式中:bG为乘车区域最外侧座位中心距线路中心线的侧向距离,取1.5 m;αa为缓和曲线起点横坡角;αe为缓和曲线终点横坡角。

若列车以匀速通过缓和曲线,则其受到的由横坡扭转产生的法向冲击为

(20)

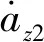
(21)

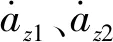
对式(22)进一步整理得式(23)

(23)

其中,

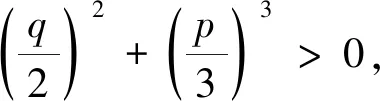
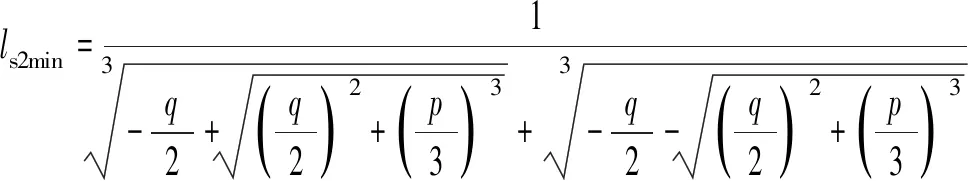
3.3 横坡扭转率确定的缓和曲线长度

因中低速磁浮交通线路采用三次抛物线型缓和曲线,其横坡角在缓和曲线上的变化规律如式(11)所示,因此,列车通过平面缓和曲线时的横坡扭转率为

(26)

式中,Δα为横坡扭转率。

由式(26)可知,缓和曲线长度与连接的圆曲线横坡角和缓和曲线上的横坡扭转率有关,根据CJJ/T 262—2017《中低速磁浮交通设计规范》中的规定,横坡扭转率在正常条件下不应大于0.12 (°)/m,困难条件下不应大于0.15 (°)/m,即正常条件下Δαmax=0.12 (°)/m,困难条件下Δαmax=0.15 (°)/m。所以,由横坡扭转率确定的平面缓和曲线最小长度为

(27)

综上所述,3个因素共同决定中低速磁浮交通最小缓和曲线长度,最终的最小平面缓和曲线长度lsmin=max{ls1min,ls2min,ls3min}。考虑与缓和曲线相连的圆曲线横坡角为2°、4°、6°,对中低速磁浮列车以20～160 km/h速度通过缓和曲线时的最小长度展开计算,其中与缓和曲线相连的圆曲线半径大小分别取附录A表A.1列车正常条件下运行时对应的建议值,中低速磁浮交通最小缓和曲线长度取值见附录A表A.3。图6为正常、困难运行条件下,侧向冲击、法相冲击、横坡扭转率对缓和曲线长度取值的影响,由图6可以发现,当横坡角为2°,列车在正常/困难条件下以20 km/h速度运行时,最小缓和曲线长度受最大横坡扭转率控制,以40～160 km/h速度在正常条件下运行时,最小缓和曲线长度受最大侧向冲击控制,在困难条件下运行时,最小缓和曲线长度受最大法向冲击控制;当横坡角为4°,列车在正常/困难条件下以20～40 km/h速度运行时,最小缓和曲线长度受最大横坡扭转率控制,以60～160 km/h速度运行时,最小缓和曲线长度受最大法向冲击控制;当横坡角为6°,列车在正常/困难条件下以20～60 km/h速度运行时,最小缓和曲线长度受最大横坡扭转率控制,以80～160 km/h速度运行时,最小缓和曲线长度受最大法向冲击控制。

图6 不同因素对最小缓和曲线长度的影响Fig.6 The effect of different factors on the length of the minimum alleviating curve

4 动力学仿真

4.1 车辆模型

以三悬浮架的(悬挂)端置式中低速磁浮车辆为例,悬浮架结构呈“口字形”框架(如图7所示),主要由2根纵梁、2个悬浮模块、4片防侧滚梁组成。

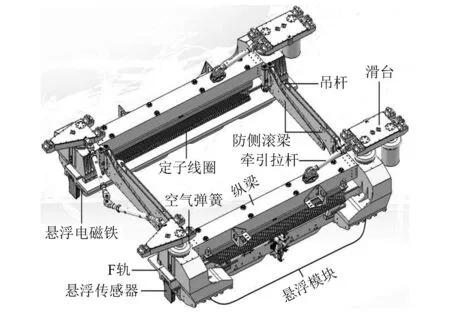
图7 (悬挂)端置式悬浮架Fig.7 (Suspension) end-set levitation frame

车辆系统由1个车体、3个悬浮架、6个牵引杆、8个滑台等部件组成,其中滑台又分为端部移动滑台和中部固定滑台。当车辆通过曲线时,移动滑台可以实现相应位置的悬浮架相对于车体发生横向位移,发生横向位移时,相应的悬浮架侧架以固定滑台为回转中心。车体和悬浮架之间还安装了迫导向机构,以此来改善车辆的曲线通过能力。对车辆结构进行适当简化,基于Simpack软件建立了具有如下微分代数方程形式的90自由度车辆系统动力学模型[19],如图8所示,图中各刚体的自由度说明见表2。

图8 车辆系统动力学模型Fig.8 Vehicle system dynamics model

表2 车辆系统自由度Tab.2 Vehicle system degrees of freedom

(28)

式中:q为各刚体的广义坐标;M为各刚体的质量矩阵;S为广义惯量;Q为作用在各刚体上的广义力矩阵;λ为拉格朗日乘子;Ф为约束雅可比矩阵;η为约束条件的加速度矢量。

4.2 悬浮控制模型

中低速磁浮车辆利用悬浮电磁铁与F轨之间的电磁吸力实现车体悬浮,电磁力F为悬浮间隙δ与悬浮电磁铁线圈电流i的函数[20]

(29)

式中:μ0为空气磁导率;A为磁极正对面积;N为线圈匝数。

根据保角变换、四角几何法[21]对式(29)分析可得悬浮力Fz、导向力Fy

(30)

(31)

式中:y为电磁铁横向位移;W为磁极宽度。

开环的电磁悬浮系统是不稳定的,遇到外部激扰时,系统容易失衡,因此需进行主动反馈控制。在实际的工程应用中,悬浮传感器可检测到悬浮电磁铁端部的悬浮间隙、加速度信号,但无法获得速度信号,悬浮间隙、加速度信号经滤波器处理后,还需引入状态观测器来重构悬浮间隙、加速度信号并构造速度信号[22]

(32)

(33)

(34)

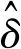
悬浮控制器利用状态观测器生成的悬浮间隙、速度和加速度信号生成控制电流

(35)

式中,k0、k1和k2分别为电磁铁悬浮间隙、垂向速度和加速度反馈系数。

由式(29)～式(35),可搭建出悬浮控制系统流程图,如图9所示,工作时两端相邻线圈串联在一起与悬浮控制器构成一套悬浮控制回路。

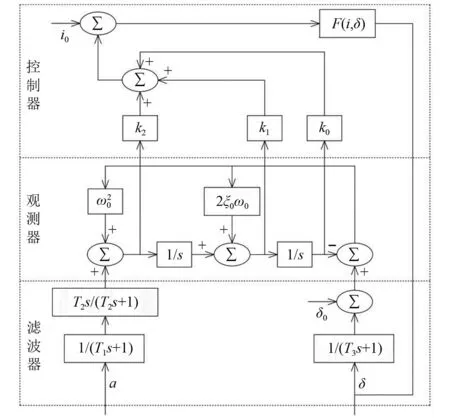
图9 悬浮控制系统流程Fig.9 Suspension control system processes

4.3 工况设置

根据理论分析得到的最小曲线半径和该半径下推导得到的最小缓和曲线长度来设置线路进行动力学仿真,对其取值的可靠性进行逐一验证,结果表明,中低速磁浮列车均能平稳地通过由上述参数设置的任意一组曲线工况。为避免赘述,本文以横坡角6°,平曲线半径970 m,缓和曲线长度120 m的曲线工况为例展开介绍,线路组成见图10,与该线路匹配的中低速磁浮列车运行速度为160 km/h。中低速磁浮列车对轨道不平顺引起的随机激励十分敏感,轨道不平顺是磁浮交通主要的外部激励源,加剧了车辆与轨道的相互作用,是造成车-轨耦合振动现象的重要因素。由于磁浮交通起步较晚,中低速磁浮轨道特殊“F”形结构也为轨道不平顺的测量产生了一定限制,目前中低速磁浮轨道不平顺的数据较少,还未形成统一的磁浮轨道不平顺功率谱轨道不平顺功率谱函数,因此本文选择文献[23]中的解析式(见式(36)),该解析式功率谱能很好的和实测线路谱相吻合,根据式(36)反演出本文仿真计算所需的轨道不平顺样本,如图11所示,轨向不平顺幅值在±2 mm内波动,高低不平顺幅值在±4 mm内波动。

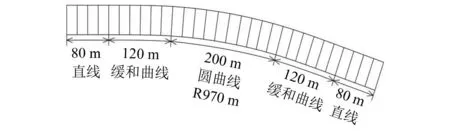
图10 线路组成Fig.10 Line composition

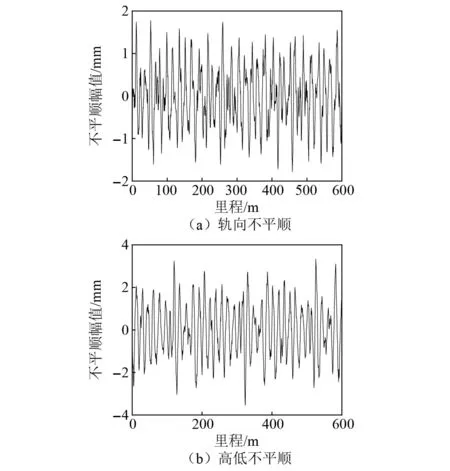
图11 轨道不平顺Fig.11 Track irregularity

(36)

式中:f为空间频率;A、B、C、D、E、F、G为轨道谱特征参数。

4.4 结果与讨论

以车体横向和垂向振动加速度、电磁铁悬浮间隙波动量和横向位移、空气弹簧横向和垂向位移为评价指标,通过动力学仿真对车辆的曲线通过性能进行评估,进而判断理论分析得到的中低速磁浮最小曲线半径及缓和曲线长度取值是否可靠。

图12所示为车辆以160 km/h的速度运行时车体的横向和垂向振动加速度时间历程曲线。图12中,Car_F、Car_R分别为车体前、后侧对应位置。

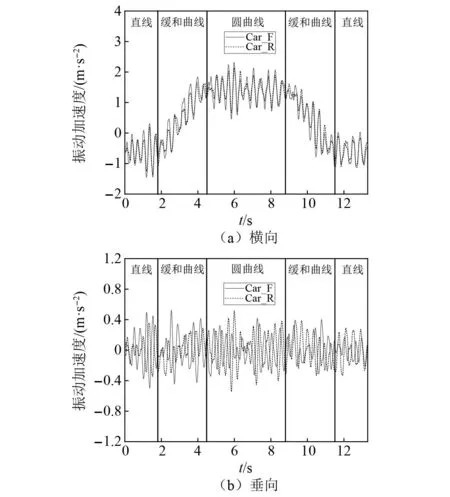
图12 车体振动加速度Fig.12 Body vibration acceleration

从图12可知,当车辆在圆曲线上运行时,车体横向振动加速度达到最大,车辆在进圆曲线的缓和曲线上运行时,车体垂向振动加速度达到最大,且最大值均出现在车体前端,分别为2.32 m/s2、0.53 m/s2,进一步得到横向、垂向平稳性最大值2.41、2.04,均小于2.5,表明车辆在曲线上运行时具有优秀的平稳性。

图13所示为车辆以160 km/h的速度运行时电磁铁的悬浮间隙波动量和横向位移时间历程曲线。图13中,L11、L14/R11、R14分别为一位悬浮架左/右侧悬浮模块前、后端电磁铁对应位置。

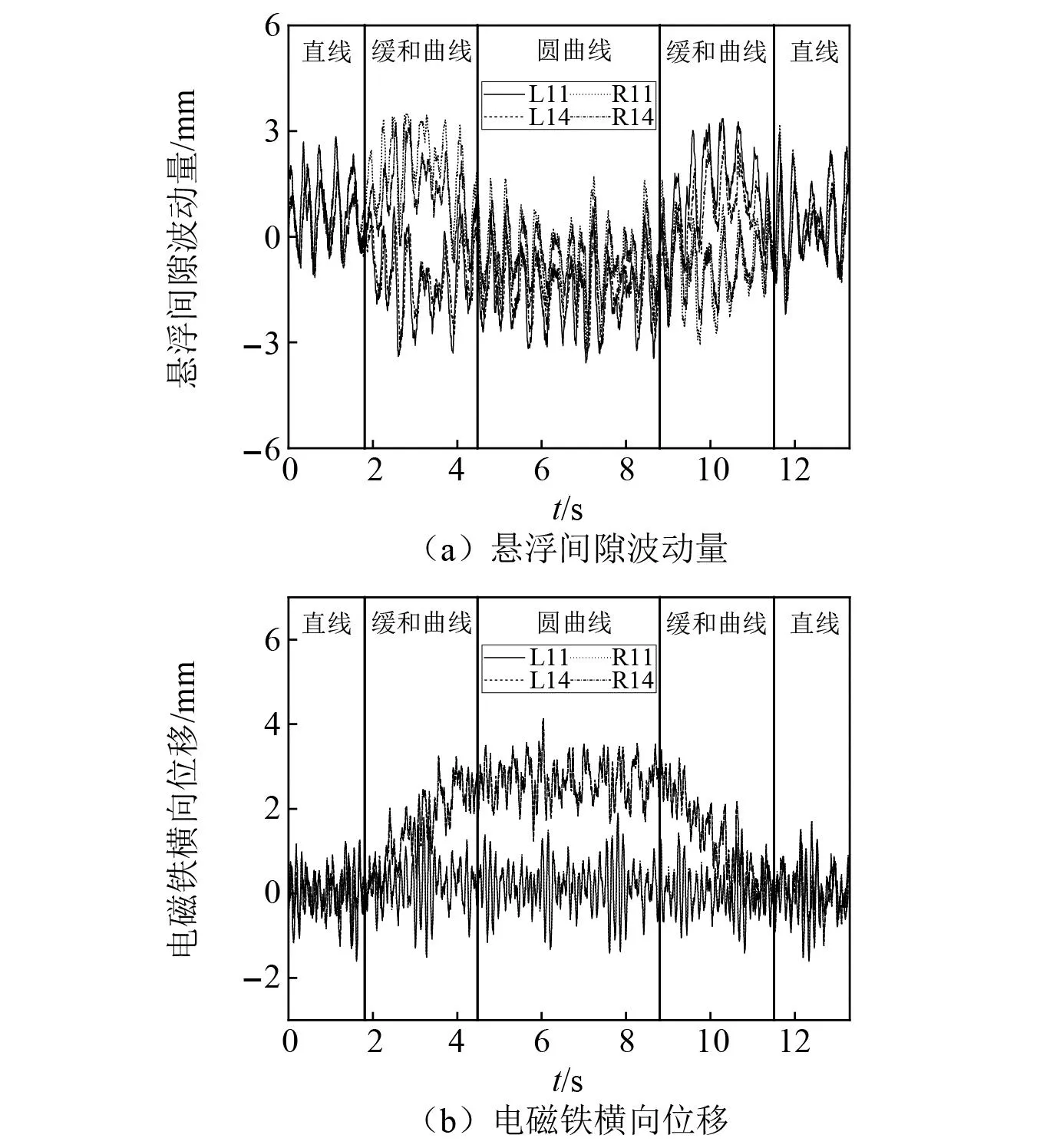
图13 电磁铁动态响应Fig.13 Dynamic response of electromagnet

计算结果表明,电磁铁悬浮间隙波动量在-3.58～3.47 mm变化,在±4 mm以内,横向位移最大值为4.12 mm,电磁铁与F轨不会发生机械碰撞,表明车辆在曲线上运行时具有良好的悬浮稳定性和导向能力。

图14所示为车辆以160 km/h的速度运行时空气弹簧的横向、垂向位移时间历程曲线。图14中,1LF、1LR/1RF、1RR分别为一位悬浮架左/右侧纵梁前、后端空气弹簧对应位置。

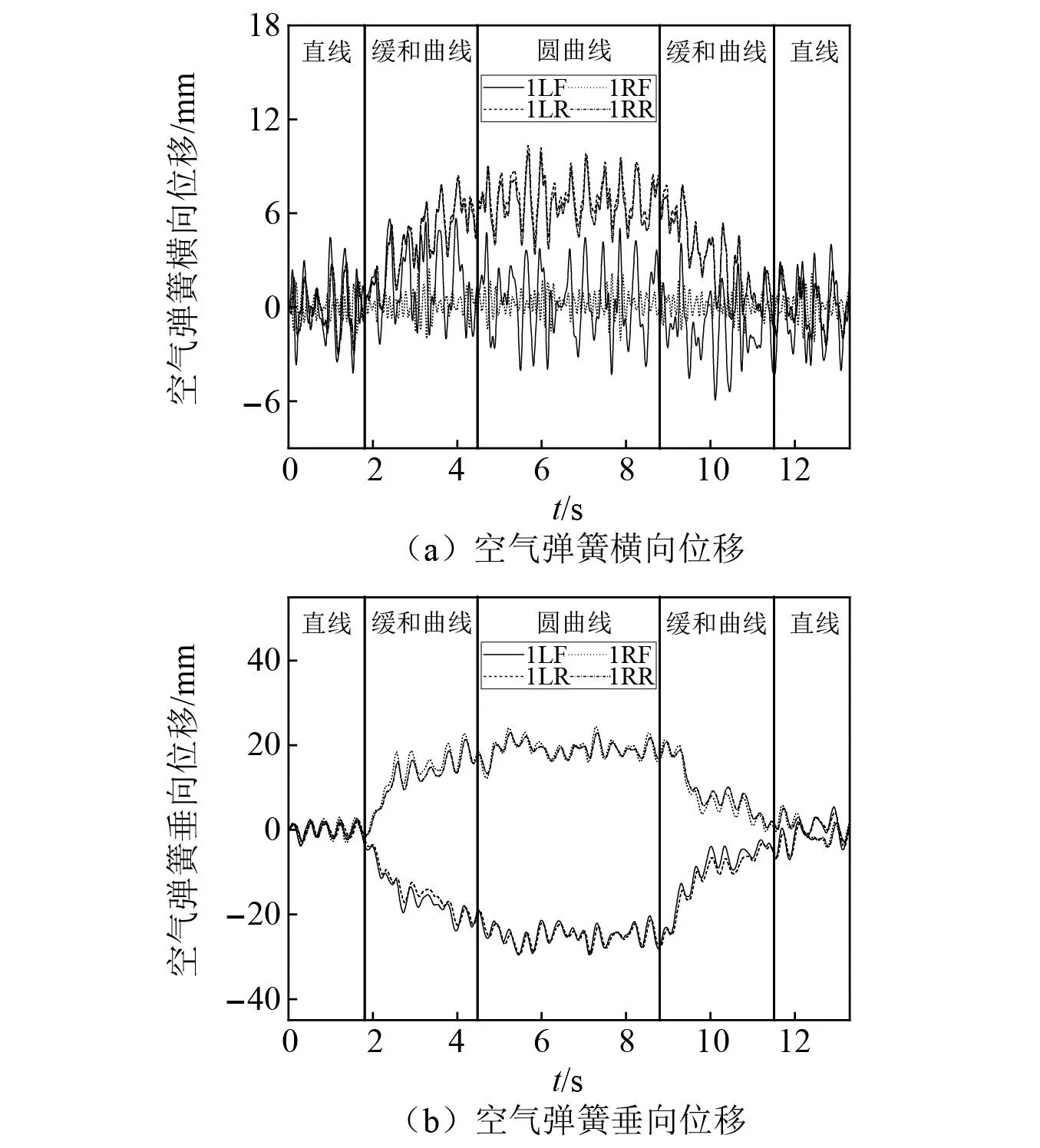
图14 空气弹簧位移Fig.14 The displacement of the gas spring

计算结果表明,当车辆在圆曲线上运行时,空气弹簧横向、垂向位移达到最大,空气弹簧的横向位移最大值为10.33 mm,出现在左侧纵梁后端空气弹簧上,垂向位移最大值为29.62 mm,出现在左侧纵梁前端空气弹簧上,空气弹簧横向、垂向位移均小于其限值。

综上所述,车辆在曲线上运行时,具有优秀的平稳性和良好的悬浮稳定性、导向能力,空气弹簧横向、垂向位移均满足规格要求。仿真结果表明,车辆曲线通过性能良好,曲线半径及缓和曲线长度取值可靠。

5 结 论

通过上述研究,可以得到如下结论:

(1)中低速磁浮列车在正常、困难条件下运行时,最小平曲线半径的取值受指向外侧的最大侧向加速度控制,最小竖曲线半径的取值受凹曲线上最大法相加速度控制,当列车运行速度一定时,横坡角越大,最小平曲线半径取值越小,而纵坡对最小竖曲线半径取值几乎无影响。

(2)当横坡角为2°,列车在正常/困难条件下以20 km/h速度运行时,最小缓和曲线长度受最大横坡扭转率控制,以40～160 km/h速度在正常条件下运行时,最小缓和曲线长度受最大侧向冲击控制,在困难条件下运行时,最小缓和曲线长度受最大法向冲击控制;当横坡角为4°,列车在正常/困难条件下以20～40 km/h速度运行时,最小缓和曲线长度受最大横坡扭转率控制,以60～160 km/h速度运行时,最小缓和曲线长度受最大法向冲击控制;当横坡角为6°,列车在正常/困难条件下以20～60 km/h速度运行时,最小缓和曲线长度受最大横坡扭转率控制,以80～160 km/h速度运行时,最小缓和曲线长度受最大法向冲击控制。

(3)理论分析得到中低速磁浮列车以20～160 km/h速度运行时可通过的最小平、竖曲线半径及缓和曲线长度,进一步给出其建议值,并通过动力学仿真对车辆的曲线通过性能进行评估,验证了取值的可靠性,可为将来中低速磁浮交通的选线设计提供理论依据和数据参考。

附录A

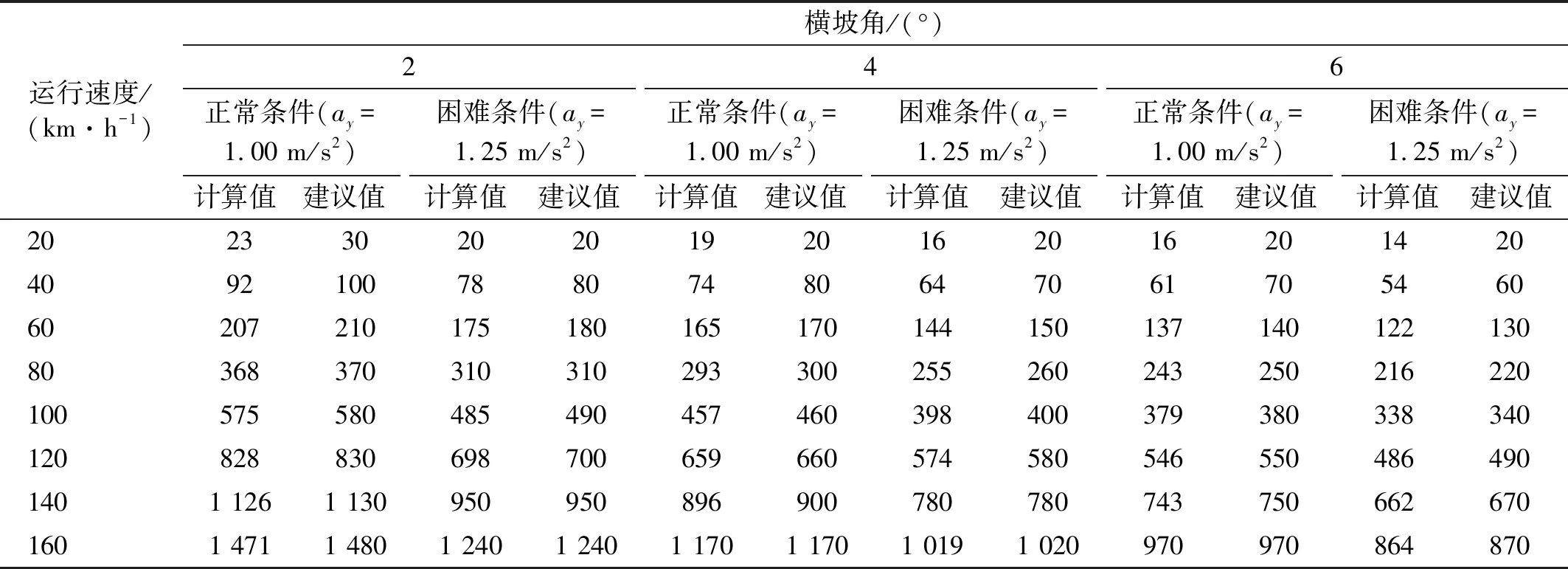
表A.1 中低速磁浮列车最小平曲线半径Tab.A.1 The minimum flat curve radius for medium and low speed maglev trains 单位:m