中国ETF期权Delta对冲收益的日夜特征研究①
刘彦初, 汤昊文, 钱潮阳
(1. 中山大学岭南学院, 广州 510275; 2. 华宝基金管理有限公司, 上海 200120)
0 引 言
随着资本市场全面深化改革的持续推进,国内期权市场体系逐渐成熟(1)据《2022年上海证券交易所股票期权市场发展报告》统计,以ETF期权为例,上海证券交易所2022年期权合约累计成交10.75亿张,累计成交面值高达38.29万亿元.、经济功能日益凸显.ETF期权作为重要的投资工具,既满足了中长期股票市场投资者增强收益、对冲风险的需求,又提升了金融市场定价效率.研究ETF期权对冲的日夜特征对于理解我国ETF期权市场和ETF现货市场联动运行机制、促进金融市场高质量发展十分关键.一方面,隔夜时段是金融市场的非交易时段,在全天时间中占比较大,对于期权做市商和持仓过夜投资者而言,隔夜时段无法及时调仓,面临更大的存货风险;另一方面,我国股票类ETF期权市场和ETF现货市场在制度上不匹配,表现为ETF市场受到诸如T+1交易制度等条件的约束,进而可能影响期权市场的定价和对冲效率.然而,我国ETF期权Delta对冲收益(简称对冲收益)的日内和隔夜特征如何、不同期权类型是否存在差异、这些特征和我国市场制度有何关系等问题尚未得到回答.在此背景下,本文基于日内和隔夜的视角对我国ETF期权的Delta对冲收益问题展开了研究.
期权Delta对冲可以看作买入一份期权的同时卖出Delta份标的资产,采用这种方法构造的投资组合一般被称为Delta对冲组合或者Delta中性组合.Delta是期权价格对标的资产价格的偏导.在Black-Scholes(BS)模型的假设下,Delta对冲收益应该等于无风险收益.然而,一些研究表明Delta对冲存在异常收益.例如,Bakshi和Kapadia[1]发现标普500指数期权的Delta对冲收益显著为负,Muravyev和Ni[2]则进一步发现Delta对冲收益存在日夜差异.这些学者从风险溢价、波动率偏差等角度进行了解释.
我国资本市场尚处于发展阶段,在市场风险偏好、交易制度等方面和海外市场存在较大差异,因此在期权市场运行机制方面可能存在较大不同.因此,本文对我国ETF期权的Delta对冲收益进行了研究,并发现以下特征:首先,总体上隔夜的Delta对冲收益显著为负,日内的收益不显著;其次,认购和认沽期权的Delta对冲收益在日内和隔夜呈现非对称的特征,即认购期权的日内收益为负、隔夜收益为正,而认沽期权恰好相反.上述结果在不同的在值程度和到期时间都稳健,使用Hull和White[3]和Xia等[4]提出的基于波动率和标的资产价格关系的Delta对冲模型并不能消除上述异象,其他一系列的稳健性检验也均支持上述结论.
针对以上发现并结合以往文献研究,本文从风险溢价、模型误差、交易制度、价格压力的角度探讨了可能的成因并进行了实证检验.首先,发现Delta对冲收益对隔夜波动率回归系数为负,这说明我国隔夜的股票ETF市场存在负的波动率风险溢价,而跳跃风险的解释力较弱;其次,认购和认沽期权的Delta对冲收益的非对称现象是由模型误差与标的资产收益共同作用产生的;进一步分析发现,T+1交易制度约束是标的资产收益出现日夜反转进而产生Delta对冲收益非对称性异象的重要原因,并且由于T+1交易制度和卖空约束的长期存在,投资者难以通过套利交易消除日内和隔夜的Delta对冲收益异象.
相关的文献研究主要涉及以下几个方面:首先是Delta对冲收益异象的研究.Bakshi和Kapadia[1]发现Delta中性组合的负收益是波动率风险溢价导致的.Broadie等[5]提出了一种新的方式度量期权收益,并且发现跳跃风险能够解释期权的Delta对冲收益.Jones和Shemesh[6]发现期权Delta对冲收益在非交易时段更低,其中绝大多数是周末,并且不能被风险因素解释,这是由于在非交易时间期权对股票波动率的不正确反应而导致的定价错误.Muravyev和Ni[2]发现美国股票市场Delta中性组合日内收益为正,隔夜收益为负,并使用波动率偏差对该现象进行了解释.
其次是波动率风险和跳跃风险的研究.Lockwood和Linn[7]发现股票的波动率在日内先降后升,并且日内的波动率显著大于隔夜的波动率.Campbell和Hentschel[8]开发了一个波动率反馈模型,研究了波动率反馈在不同波动率水平下和股票收益的关系.Grleanu等[9]对期权的需求压力效应进行了建模,理论模型证明了在期权需求定价模型的框架下,期权价格和无法对冲的风险(标的价格的跳跃、随机波动风险)正相关.Carr和Wu[10]提出了一种方法来测量金融资产的波动率风险溢价.Hull和White[3]考虑了期权隐含波动率和标的资产价格的关系,并提出了一种新的方差最小对冲方法.郑振龙和秦明[11]发现从时间维度上来看,尤其是在牛市样本中,我国期权被明显高估.陈蓉等[12]发现上证50的波动率风险溢价为负,且具有明显的时变特征.刘杨树等[13]和陈淼鑫和武晨[14]从跳跃风险的角度对期权的对冲收益等进行了研究.夏泽宇和高峰[15]构造了夜间波动率占比指标,发现夜间波动率占比能够解释全天超额波动率以及波动率溢价.
除了上述经典文献以外,本文的研究还与模型误差、标的资产日夜收益相关.在模型误差研究方面,Branger和Schlag[16]发现只有在理想连续的情形以及模型设定正确的情况下,Delta对冲收益才能识别波动率风险溢价.郑振龙和刘杨树[17]发现在存在模型误差的情况下,标的资产价格过程的漂移项会影响Delta对冲收益.Grleanu等[9]认为离散化风险等因素会放大做市商的存货风险.在标的资产日内和隔夜收益研究方面,Lou等[18]认为不同投资者的过度需求导致了股票日内和隔夜收益的反转.张兵[19]发现在T+1交易制度下,投资者在开盘的买入风险更大因而需要补偿,导致股票市场隔夜回报为负.Bogousslavsky[20]研究了日内和隔夜股票回报的横截面变化,发现制度限制和隔夜风险激励了套利者在收盘前根据错误定价进行交易以减少头寸.张兵和朱红兵[21]发现A股标的风险越大,其隔夜收益率相比于H股的折价程度就越大.
最后,相关的研究还包括到期权特征、市场制度、需求压力等方面.Bakshi等[22]发现短期和长期的期权合约蕴含了不同的信息,在引入了随机利率模型以后可以改善长期合约的对冲效果.Bakshi等[23]认为U型的定价核可以解释期权的回报.Santa-Clara和Saretto[24]发现交易摩擦和保证金要求影响了期权卖方的收益,限制了市场流动性.乔帅等[25]研究了台指期权市场散户的交易行为.郑振龙等[26]研究了50ETF 期权“净购买压力”指标,发现该指标能够预测指数的方向和波动.
本文的贡献主要有以下几点.第一,多数学者在研究Delta对冲收益时未对日内和隔夜进行区分,忽略了隔夜时段的重要性.本文则重点研究了Delta对冲收益的日内和隔夜特征.第二,本文发现,波动率风险溢价是我国ETF期权隔夜对冲收益为负的主要原因;Muravyev和Ni[2]提出的波动率偏差和Jones和Shemesh[6]提出的非交易时间效应在中国市场并不具有解释力.第三,以往研究没有考虑T+1交易制度对期权对冲的影响,本文则详细论证了T+1制度约束如何导致了认购和认沽期权对冲收益的非对称性.第四,在注册制改革的背景下,资本市场的市场化程度也会越来越高,本文的发现为金融监管层未来可能逐步放开T+1制度和减少卖空约束提供了一定的依据.总之,本文丰富了我国期权对冲收益日夜特征的研究,一方面有利于投资者更好地进行风险管理和投资,另一方面也可以为监管层理解市场行为和完善资本市场交易制度提供启发,从而进一步推进资本市场全面深化改革,助力中国特色现代资本市场建设.
1 数据与度量
选取了我国上市的三种ETF期权,分别是上交所的华夏上证50 ETF(记为50ETF.SH,代码510050)期权、深交所的嘉实沪深300 ETF(记为300ETF.SZ,代码159919)期权和上交所的华泰柏瑞沪深300 ETF(记为300ETF.SH,代码510300)期权.本文选取50 ETF期权2015年2月9日~2021年6月4日的日度数据,由于300ETF期权上市时间较短,所以只选取2019年12月23日~2021年6月4日的日度数据.数据来源为国泰安数据库.
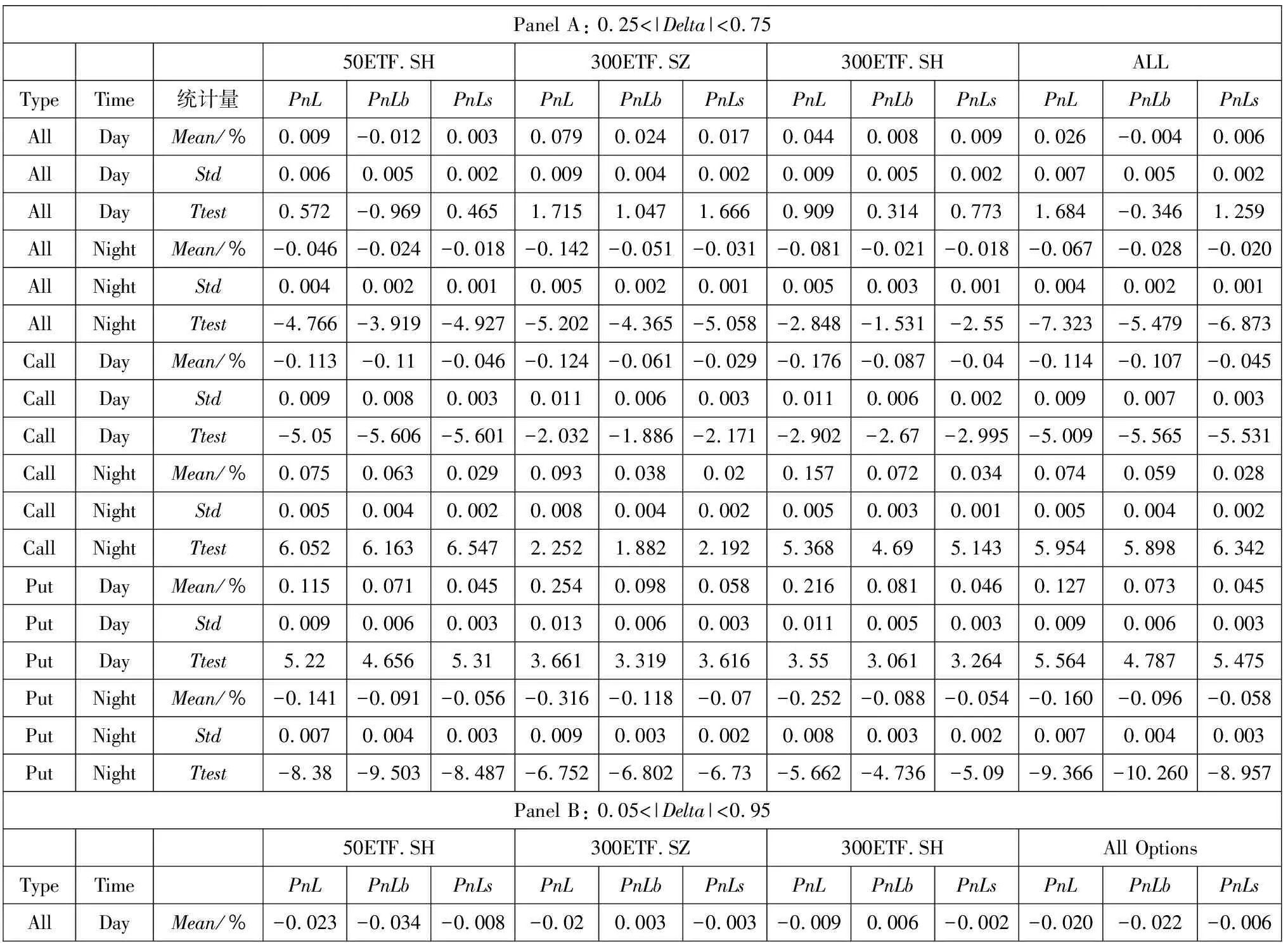
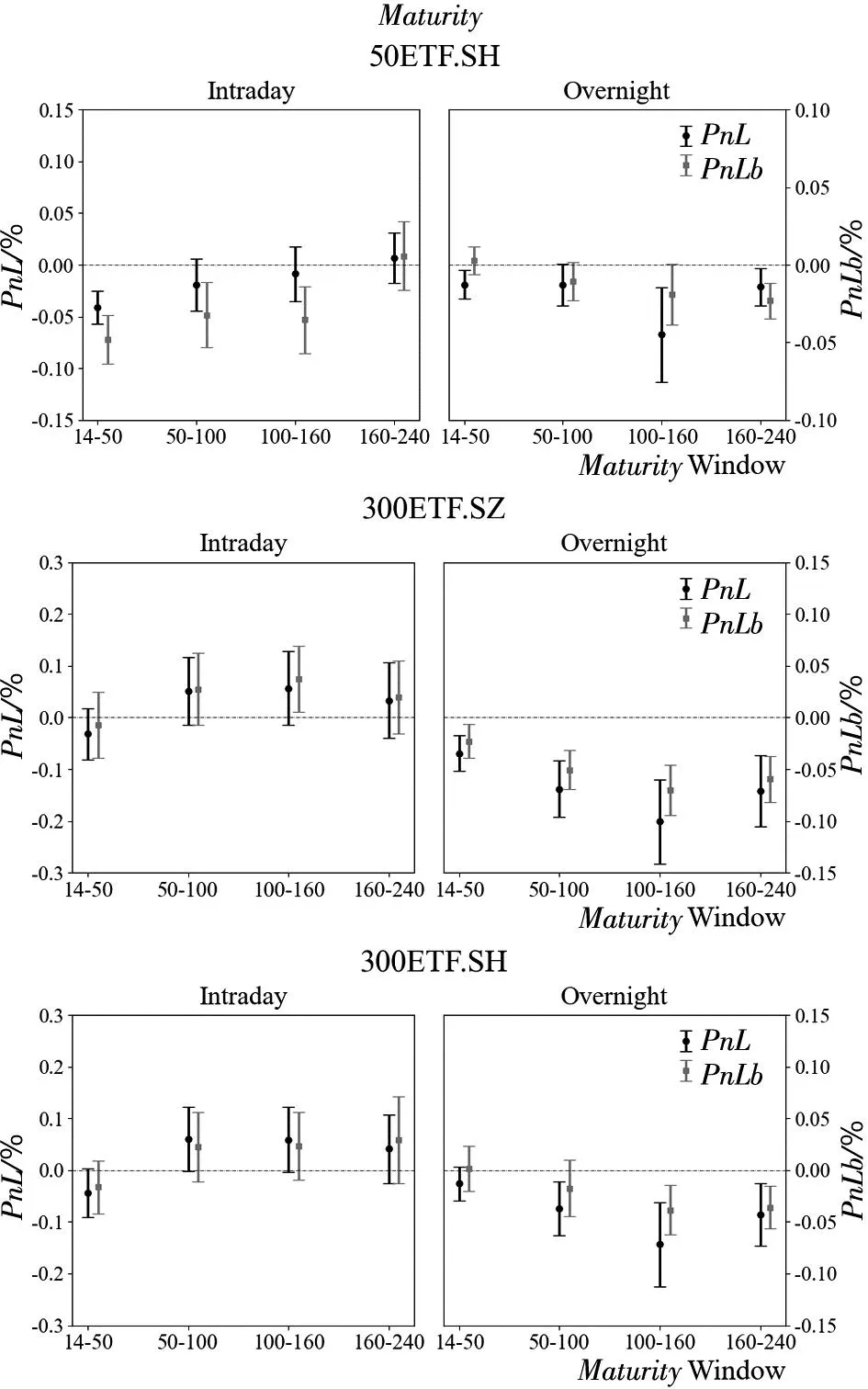
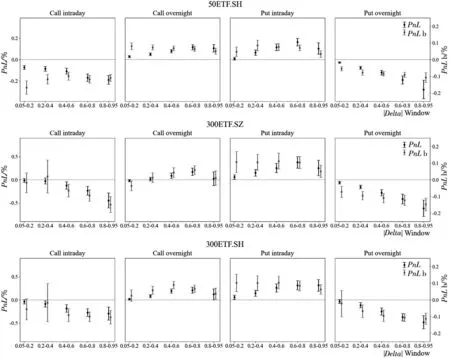
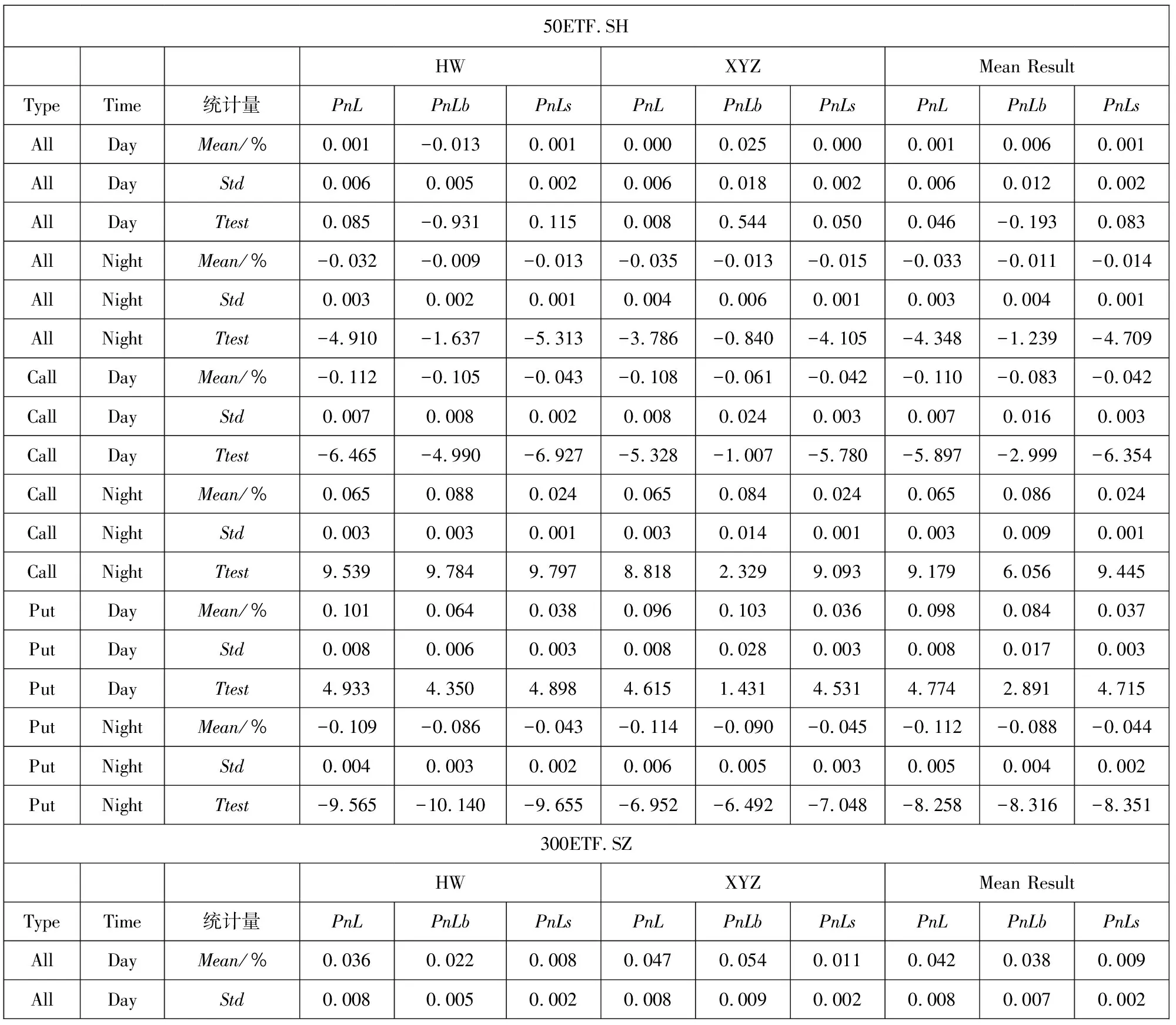
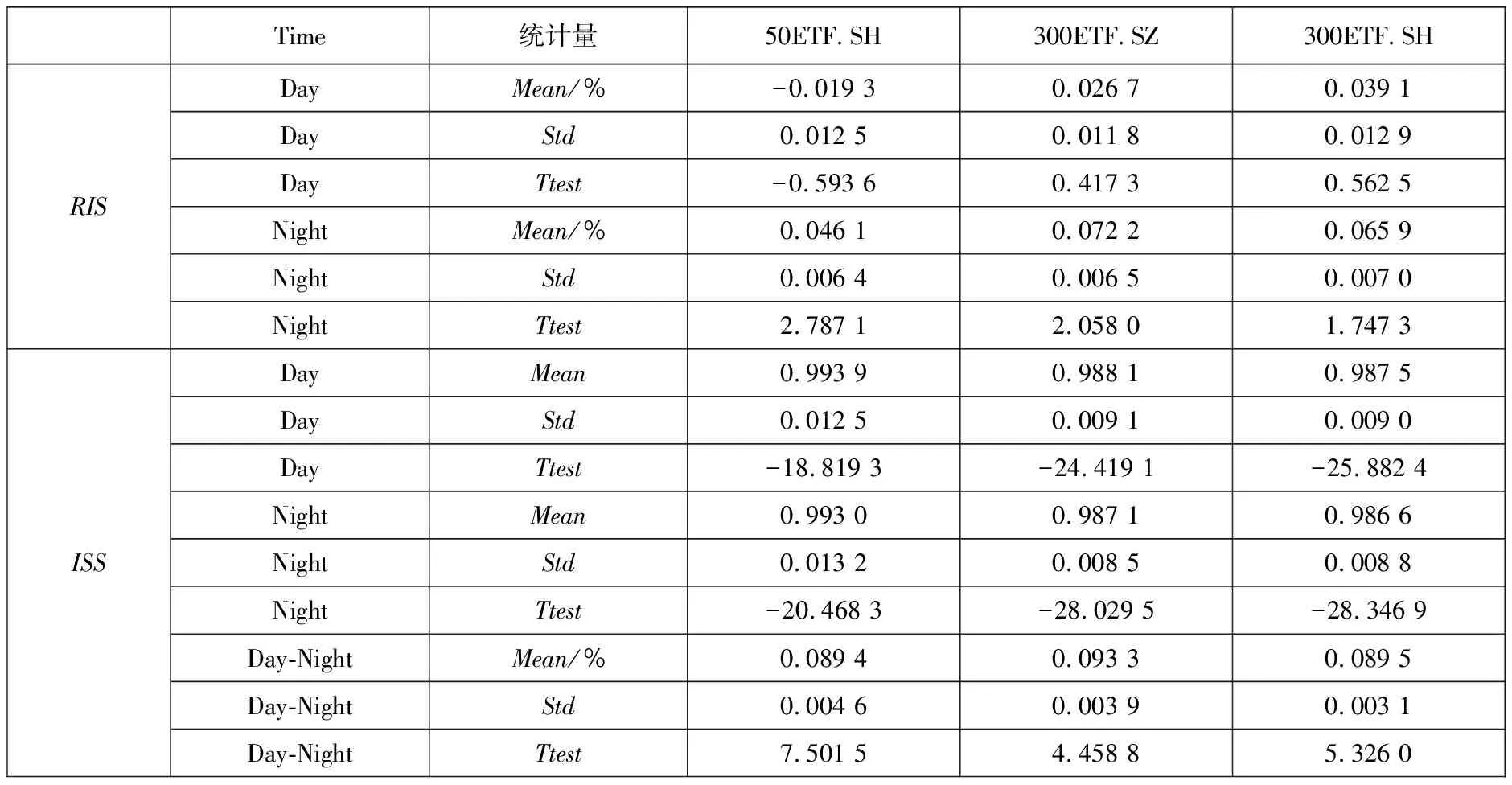
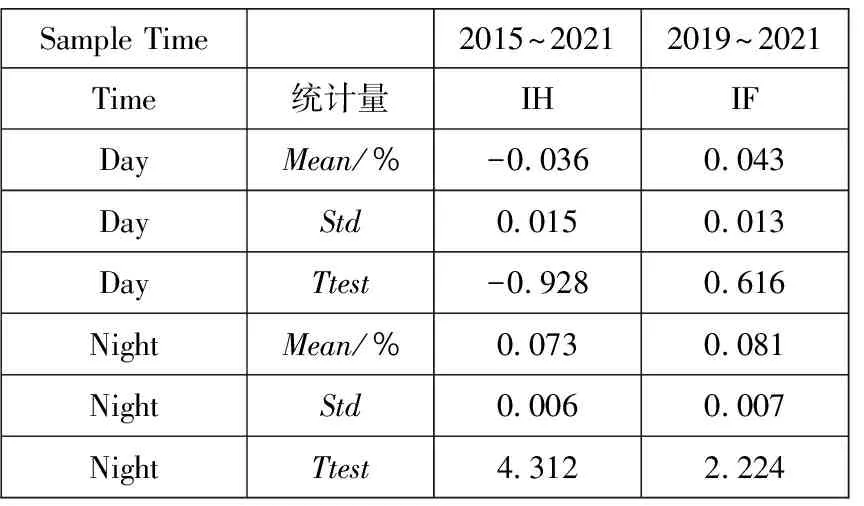
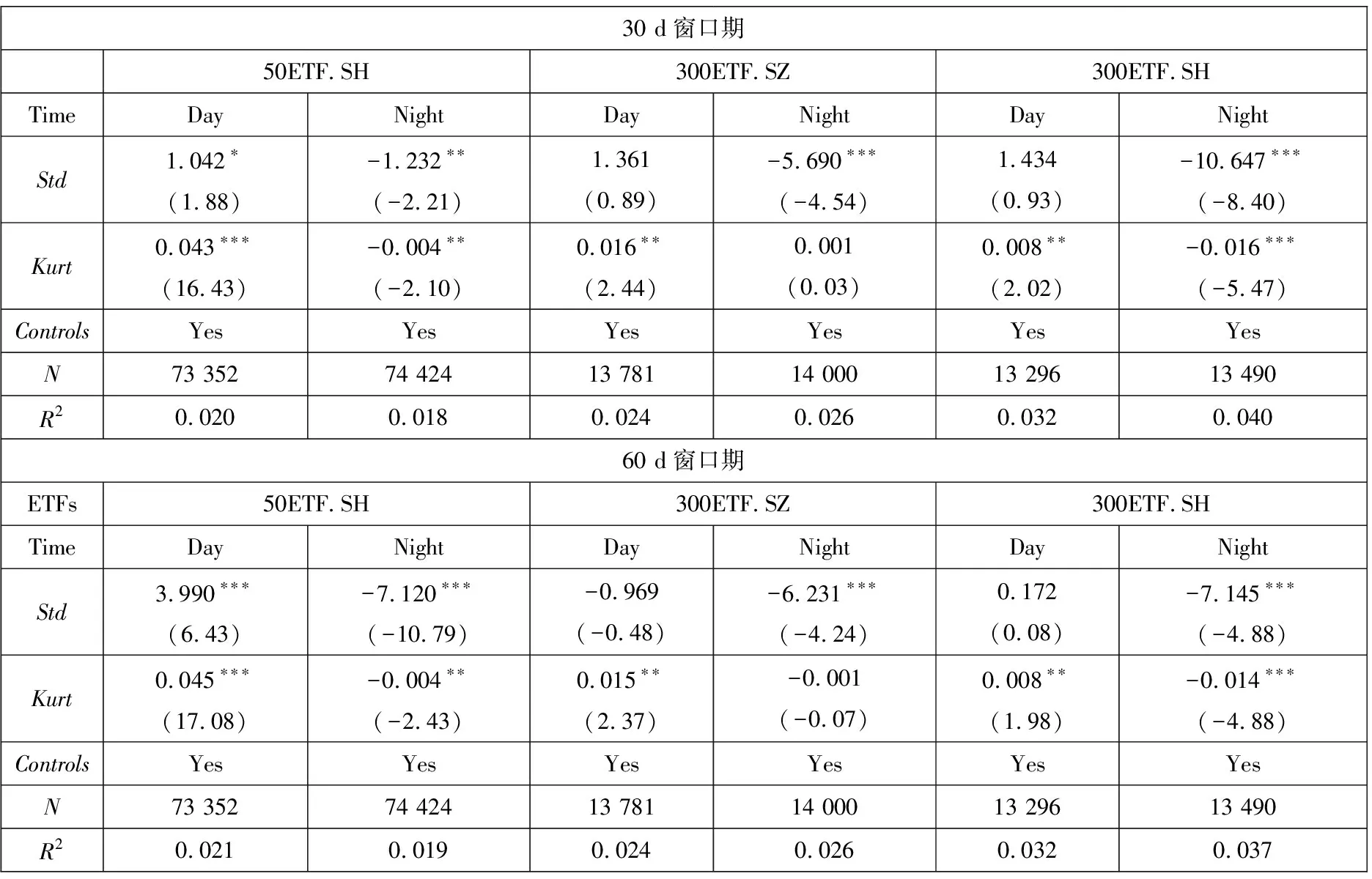
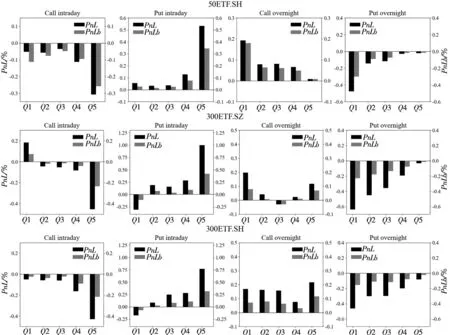
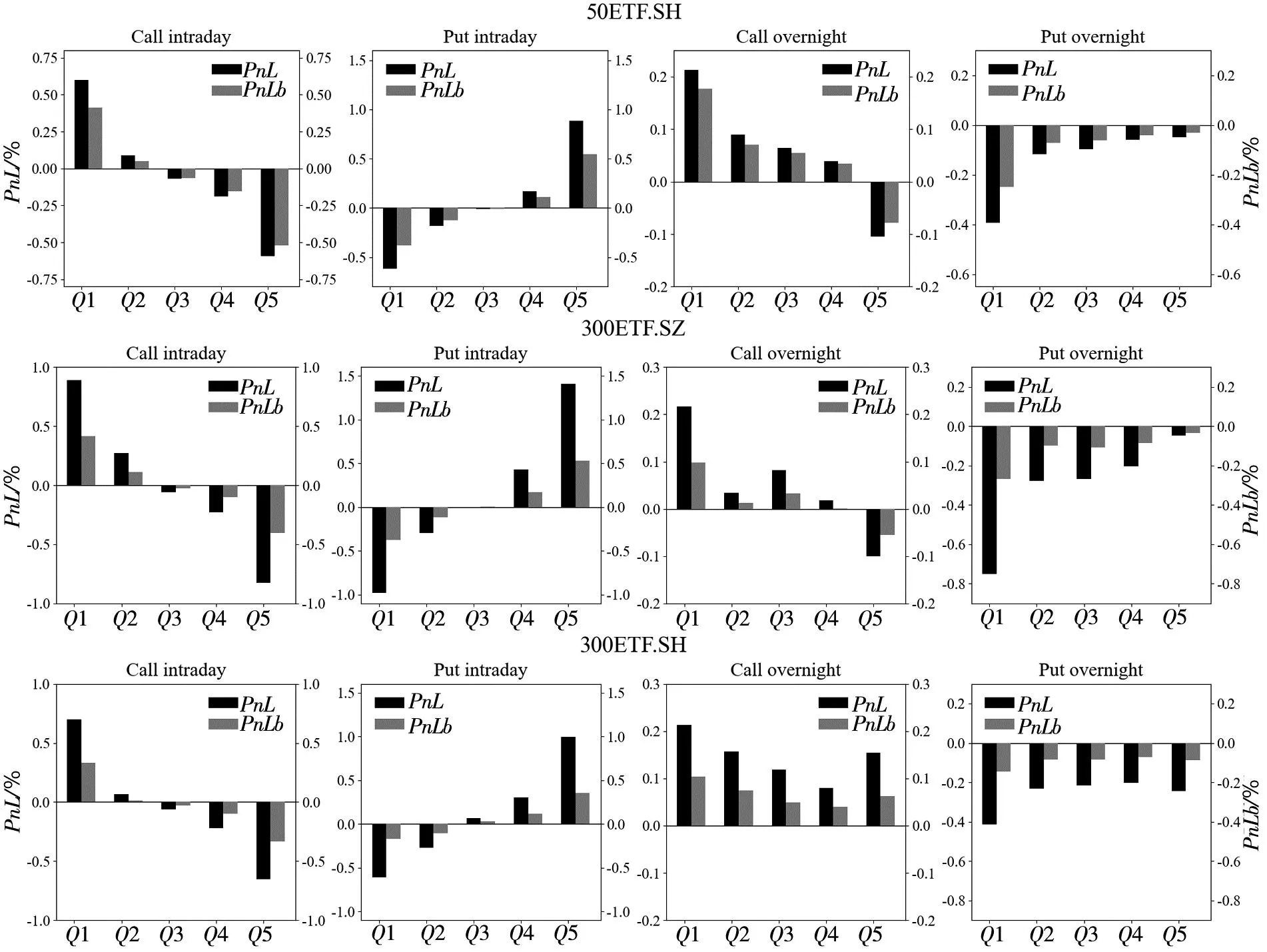
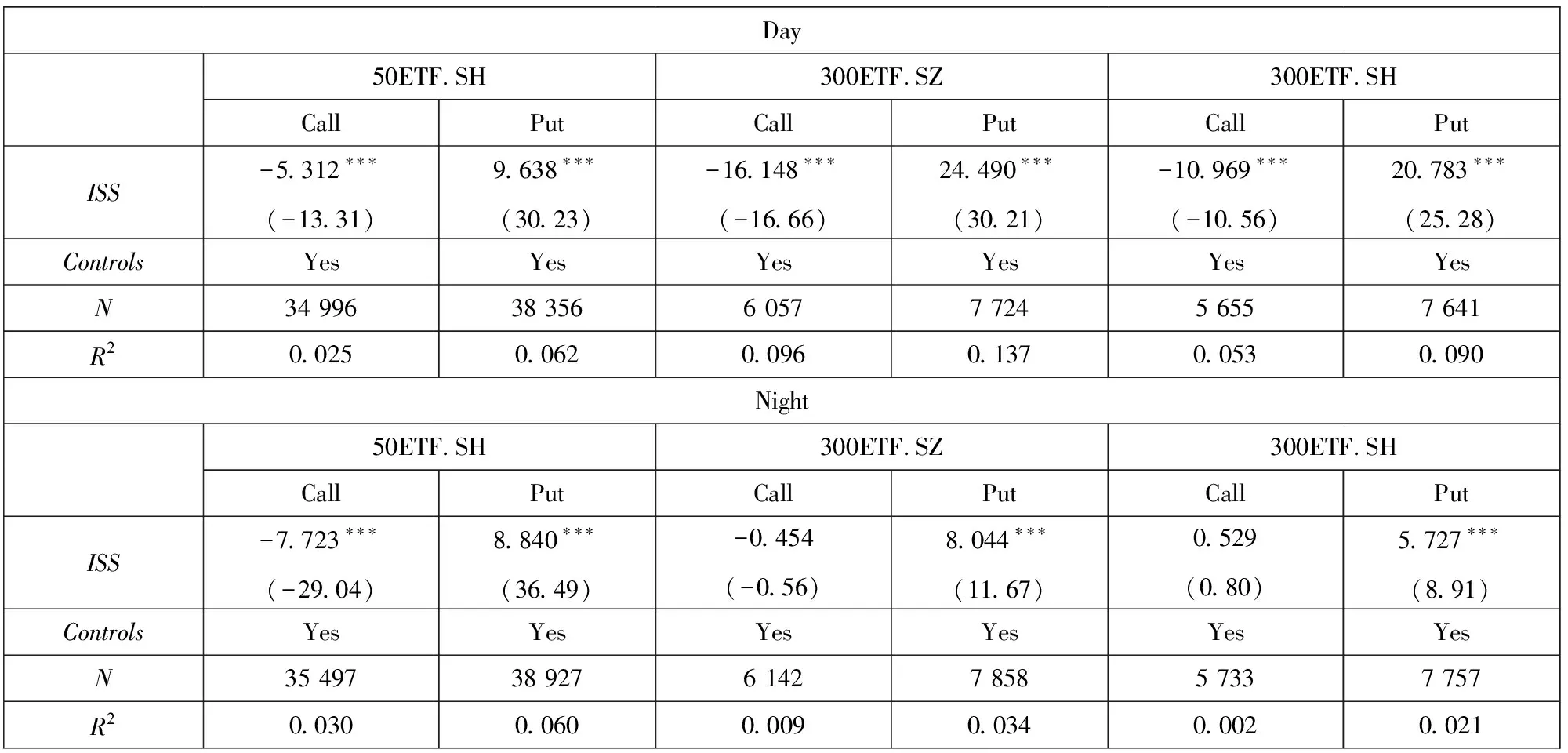
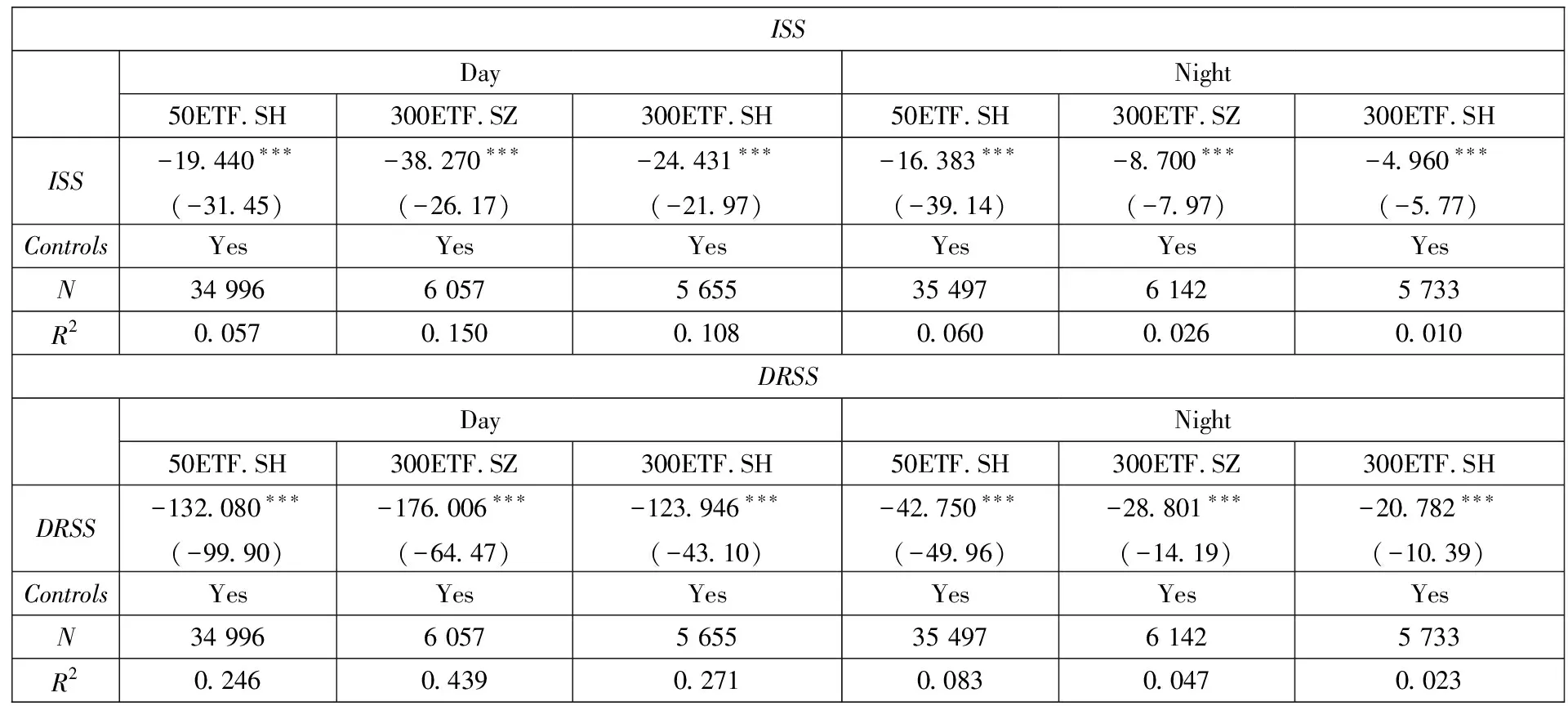
为避免极端值等因素的影响,综合考虑Bakshi和Kapadia[1]、Muravyev和Ni[2]等学者的处理方法,设定了以下筛选条件:到期时间在14 d~240 d内;去除成交量为0的样本;隐含波动率在0.01~1之间;认购期权价格范围是S-Ke-rτ PnLt+τ=ft+τ-ft-Δt(St+τ-St)- (1) 其中τ表示到期时间,r表示无风险收益率,f表示期权价格,S表示标的资产价格,Δ表示对冲比率Delta,N取365.无特殊说明的情况下本文使用BS模型的Delta作为期权的对冲比率,即用隐含波动率(IV)计算Delta值. 式(1)中最后一项数值较小,其影响可以忽略不记,且参考Muravyev和Ni[2]的处理方法,假设无风险收益率为零,式(1)即为 PnLt+τ=ft+τ-ft-Δt(St+τ-St) (2) 表1分别展示了|Delta|处于区间0.25~0.75(Panel A)和0.05~0.95(Panel B)的结果(5)具体计算步骤是:先对每期所有合约的Delta对冲收益取均值,记为Rt,再对R1,R2,…,RN进行统计分析..从总体(All)来看,我国ETF期权Delta对冲收益在隔夜显著为负,在日内则不能显著拒绝均值为零的原假设.当|Delta|处于区间0.25~0.75,全样本的结果(All Options)显示日内PnLb均值为-0.004%(t值-0.346),隔夜PnLb均值为-0.028%(t值-5.479);当|Delta|处于区间0.05~0.95,PnLb均值为-0.022%(t值-2.115),隔夜PnLb均值为-0.025%(t值-4.917).50ETF的日内Delta对冲收益在0.05<|Delta|<0.95的情况下变为显著,这说明深度实值和深度虚值对50ETF的日内对冲收益影响较大. 表1 Delta对冲收益的日夜特征 从认购(Call)和认沽(Put)期权的差异性来看,三种ETF期权的Delta对冲收益均呈现出非对称性.这种非对称性表现为认购期权的对冲收益日内为负、隔夜为正,认沽期权则是日内为正、隔夜为负.所有期权品种的结果(All Options)显示,在|Delta|处于区间0.25~0.75,认购期权的日内PnLb均值为-0.107%(t值-5.565)、隔夜PnLb均值为0.059%(t值5.898),认沽期权的日内PnLb均值为0.073%(t值4.787)、隔夜PnLb均值为-0.096%(t值-10.260);在|Delta|处于区间0.05~0.95可以得到相似的结果.进一步分析发现,认购期权和认沽期权Delta中性组合日夜收益绝对值大致相等且二者符号相反;对于隔夜收益,虽然认沽期权和认购期权的Delta对冲收益符号相反,但是认沽期权的隔夜收益绝对值更大.因此,如果仅考虑总体的结果,就会低估不同类型期权对冲误差的影响. 对比以往文献研究,本节考察了仅收盘调仓(不区分日夜)的情形,三种ETF期权的Delta对冲收益均为负,其中50ETF期权的Delta对冲收益显著为负, 这与陈蓉等[12]的结果一致.这暗示仅收盘调仓的对冲收益可能主要来源于隔夜部分,间接说明了区分日内和隔夜对冲收益的必要性.此外,Muravyev和Ni[2]发现美国市场期权的Delta对冲收益日内显著为正、隔夜显著为负,并且认购期权和认沽期权都是日内为正、隔夜为负.然而,他们发现FXI期权的日内平均收益显著为负,隔夜平均收益为正但不显著.FXI期权是以我国公司股票为标的资产(iShares China Large-Cap ETF,简称FXI(6)iShares China Large-Cap ETF 是追踪在香港上市的市值排名前50的中国内地企业.)且在美国上市的期权.FXI的日内交易时间正好对应我国的隔夜时间(7)美国市场和中国市场交易时间是错位的,美国日内交易时间为9:30~16:00,以美国夏令时为例,换算成北京时间是21:30~次日4:00,冬令时则延后1 h.中国的日内交易时间为北京时间9:30~11:30、13:00~15:00.,因此与本文的主要结论是一致的. 本节检验了Delta对冲收益与不同到期时间、在值程度的关系.为此按照样本分布情况将到期时间划分为14 d~50 d、 50 d~100 d、 100 d~160 d、 160 d~240 d,将在值程度(Delta绝对值)划分为0.05~0.2、 0.2~0.4、 0.4~0.6、 0.6~0.8、 0.8~0.95. 图1考察了全样本情况下(不区分认购和认沽)不同到期时间和在值程度的Delta中性组合的日夜收益特征.随着到期时间增加,隔夜收益呈现下降趋势且符号为负,而日内收益则呈现上升趋势.另外,随着实值程度的增加,隔夜收益也呈现下降趋势且符号为负,日内收益则不确定. 注:左侧和右侧分别展示了不同到期时间和不同在值程度下的Delta中性组合日夜收益.其中每个子图的左侧纵坐标表示PnL,右侧纵坐标表示PnLb,单位是%.垂直线段表示95%的置信区间. 图2、图3分别考察了认购和认沽期权在不同到期时间和在值程度下Delta中性组合的日夜收益特征,可以看到总体上结果与表1的结论一致,认沽期权和认购期权日夜收益呈现明显的非对称特征.从到期时间看(图2),随着到期时间的增加,认沽期权收益的绝对值逐渐变大,认购期权则基本持平.这一现象说明,到期时间越长认沽期权对冲的效果越差.从在值程度看(图3),随着期权实值程度的增加,Delta对冲收益的绝对值呈现逐渐增加的趋势.总之,Delta对冲收益的特征在不同到期时间和不同在值程度的情况下结果仍然稳健. 图2 Delta对冲收益与到期时间 图3 Delta对冲收益与在值程度 股票收益率和波动率存在相关性[27, 28],即杠杆效应.Bakshi和Kapadia[1]认为正是这种相关性产生了波动率风险溢价.Hull和White[3]发现杠杆效应导致BS模型Delta对冲存在较大误差,因此在最小方差对冲比率的框架中引入了波动率对标的价格的偏导.Xia等[4]在此基础上进一步改进了估计方法,考虑了股票价格和隐含波动率的动态关系,即假设“杠杆”服从O-U随机过程.本节基于上述两种改进的方法重新检验了Delta对冲收益.下文分别将Hull和White[3]和Xia等[4]的方法记为HW方法和XYZ方法.在HW方法部分,选取半年作为窗口期并按日滚动计算;在XYZ方法部分,先选取一个月的窗口期计算价格敏感度,后选取半年的窗口期按月滚动计算对冲系数. 表2展示了上述两种方法的结果,并给出了两种方法的平均统计结果(Mean Result).可以看到总体上对冲收益显著性有所下降,其中50ETF.SH隔夜的PnLb指标不显著,并且部分认购期权的对冲收益变为不显著,但是总体上仍然存在认购和认沽期权对冲收益的非对称性.一方面,基于波动率和标的资产价格关系的方法部分降低了对冲误差,这说明改进后的模型一定程度上识别到了波动风险溢价;另一方面,虽然这些方法针对BS模型的Delta进行了改进,但是仍然无法解释认购和认沽期权对冲收益的非对称性. 表2 基于波动率和标的资产价格关系(0.25<|Delta|<0.75) 本节考虑了7种稳健性检验: 1)由于收益率可能存在异方差和自相关性,所以考虑Newey-West调整后的t值; 2)采用一年期国债利率作为无风险利率,检验无风险收益率的影响,即式(1); 3)不同的波动率计算方式得到的Delta不同,因此用实现波动率计算Delta; 4)由于手续费可能会影响实际的收益,因此加入了手续费因素,具体设定是 ETF期权单张手续费取1.6元,标的资产单笔交易收取交易额的0.004%; 5)使用50ETF的日内一分钟数据,对50ETF一小时调仓一次; 6)BS模型并未考虑波动率的动态特征,因此对基于Heston模型的Delta对冲收益进行检验; 7)考虑到股票ETF采用T+1交易制度且存在卖空约束,本文也采用了相应的股指期货进行对冲(8)详情见3.1.4节部分..上述检验的结果都是稳健的,尤其是认购和认沽期权的非对称性在所有检验结果中均显著(9)此处省略稳健性结果,有需要的读者可以向作者索取.. 下面将分析两个问题:一,如何解释总体上 ETF期权的Delta对冲隔夜收益显著为负;二,如何解释认购和认沽的非对称性.借鉴以往学者的研究,本节将从不同的角度进行探讨,具体包括波动率风险溢价[1, 16]、波动率偏差[2]、跳跃风险溢价[1, 5, 13]、模型误差风险[13, 16, 17]、交易制度[19, 21, 29]、价格压力[9, 18]. 3.1.1 波动率风险溢价 波动率风险溢价是影响期权定价和对冲的重要因素.现实中隐含波动率往往高于实际测度下的波动率,这意味着期权买方需要向期权卖方支付一部分溢价,一般被称为波动率风险溢价.波动率风险溢价的来源是多方面的,例如:期权买方有对冲风险或投资的迫切需求,或者期权卖方难以对冲自身风险[9]等.根据模型的不同,波动率风险溢价的检验可以分为以下两种方法: 第一种波动率溢价检验方法是基于BS模型构造的.在经典BS模型假设下,波动率风险溢价表现为隐含波动率和实际波动率的差异.根据Muravyev和Ni[2],期权对冲的收益可以表示为 (3) VRPt=E(σt,t+τ)-E(σt,t+τ) (4) 其中实际测度下的波动率E(σt,t+τ)可以用实现波动率替代,风险中性测度下的波动率E(σt,t+τ)可以用iVIX(10)iVIX的计算参考芝加哥期权交易所VIX指数(CBOE Volatility Index)的编制方法,这是一种无模型的期权隐含波动率计算方法.代替.然而,由于日内和隔夜的实际时间跨度不同,实现波动率难以在统一量纲下比较.虽然Muravyev和Ni[2]采用实际时间作为权重对波动率进行调整,但是简单按照真实时间权重进行调整仍存在一定的主观性. 另一种波动率溢价检验方法是基于随机波动率模型(Stochastic Volatility Model)构造的,Bakshi和Kapadia[1]认为预期的Delta对冲收益可以表示为 λφt(τ)Stσt (5) λu表示标的资产收益率和波动率的相关性,φt(τ)为正(11)详见Bakshi和Kapadia[1]中的命题2.,即Delta对冲收益应该和σ负相关.该方法的优点在于无需对波动率进行调整,基于该方法本文提出: 假设A总体上,隔夜的实现波动率和Delta对冲收益负相关. 3.1.2 跳跃风险溢价 期权价格不仅反映了预期的波动率风险,同样也反映了预期的尾部风险(跳跃风险).跳跃风险是期权定价的重要因素[1, 13, 30].Bakshi等[30]采用无模型的方法计算风险中性测度下的偏度和峰度.其中,风险中性的偏度(Skew)反映跳跃幅度,风险中性的峰度(Kurt)反映跳跃强度. 根据Bakshi和Kapadia[1]和Branger和Schlag[16],在引入跳跃过程的随机波动率模型下,跳跃风险对于Delta中性组合的影响有两条路径:第一,对于认购期权,一般情况下跳跃幅度均值(风险中性的偏度)和认购期权Delta对冲收益正相关,和认沽期权Delta对冲收益负相关;第二,Delta对冲收益与风险中性的峰度负相关.基于上述理论本文提出: 假设B1风险中性的偏度与认购期权的Delta对冲收益正相关,与认沽期权的Delta对冲收益负相关; 假设B2风险中性的峰度与期权Delta对冲收益负相关. 3.1.3 模型误差与标的资产收益 Branger和Schlag[16]发现只有在连续交易以及模型设定正确的情况下,Delta对冲收益才能完全由波动率风险溢价和跳跃风险溢价解释.现实中投资者一般采用模型的方法进行对冲.然而,模型的假设往往与现实情况不符,因此可能会产生较大的对冲误差.刘杨树等[13]在实证检验中引入了标的资产收益作为模型误差因子.郑振龙和刘杨树[17]发现在假设模型存在较大误差的情况下,标的资产收益会影响衍生品的定价和复制,一段时间内Delta对冲的累积误差可以表示为 (6) 在标的资产收益方面,表4展示了标的资产的日内和隔夜的平均收益(12)这里选取与期权上市时间一致的时间段,除此之外,本文还对ETF成立以来的所有数据进行了检验,发现除了300ETF(159919)的隔夜收益不显著,其他ETF均呈现显著的日内为正和隔夜为负的特征.,可以看到标的资产日夜收益存在反转效应.具体而言,50ETF 期权的日内收益显著为正,平均每日为0.086%,隔夜收益显著为负,平均为-0.04%,另外300ETF的日内收益显著为正的0.12%,隔夜收益虽然不显著,但是平均来看为负.这些发现与张兵[19]发现的我国股票日内和隔夜收益的结果一致.模型误差和标的资产收益的共同作用导致了认购和认沽期权的日夜收益的非对称性.具体影响途径是,认购期权的Delta普遍高估,即deltaerror,t为正,所以对冲收益和标的资产收益方向一致,又因为标的资产收益隔夜为负、日内为正,最终导致了认购期权对冲收益日内为负、隔夜为正,而认沽期权普遍低估,因此导致了相反的结果. 综上,由于标的资产收益存在日夜反转效应,因此PnLbt对deltaerror,t×dSt的回归系数应该与对deltaerror,t×dSt-1的回归系数符号恰好相反.通过以上分析,本节提出以下假设: 假设C1当期Delta对冲收益对当期标的资产收益的交互项的回归系数为负; 假设C2当期Delta对冲收益对上一期标的资产收益的交互项的回归系数为正. 3.1.4 T+1交易制度 我国股票类ETF和股票一样受到T+1制度的限制.张兵[19]认为由于T+1交易制度的限制,ETF投资者无法在日内连续交易.一方面,开盘买入股票的投资者只能隔天才能卖出,因此需要获取一定的风险溢价补偿;另一方面,t期买入股票的投资者在t+1期开盘积压了卖出压力.最终导致了ETF价格开盘相对于收盘价偏低. 接下来,将从期权隐含标的资产和期货的角度分析T+1制度的影响.期权隐含的标的资产价格(以下简称期权隐含价格)是由期权价格反推出来的,由于期权市场本身没有T+1制度的限制,可以通过对比期权隐含价格和标的资产实际价格(以下简称实际价格)分析T+1制度带来的影响. 首先,利用期权平价公式,即 ImpliedSt=Ct-Pt+Ke-rτ (7) 构造了期权隐含价格的收益率(记为RIS) (8) 表5展示了RIS的统计量,三种期权的RIS均表现出隔夜显著为正、日内不显著的特征,正好与表4的标的资产的实际收益率特征相反. 表5 期权隐含的标的资产收益 其次,本文构造了期权隐含价格和实际价格的比值(记为ISS) (9) 其中ISS衡量了某时刻实际价格相对于期权隐含价格的低估程度,ISS越大表示实际价格相对于期权隐含价格越低.由表5可知,三种ETF期权的ISS存在明显的日夜差异,表现为日内(开盘)ISS值显著大于隔夜(收盘)ISS值,这表明相对于收盘时刻,开盘时刻的期权隐含价格较大、实际价格较小.因此,T+1制度在开盘时刻压低了实际价格,导致期权隐含价格和标的资产价格的分歧程度在开盘和收盘时刻存在差异.这种分歧程度差异本质上是因为经典期权定价模型假设市场交易无摩擦与现实的T+1制度不一致.在T+1的约束下,纵使标的资产的价格和期权隐含价格出现了明显异象,投资者也难以通过套利消除异象,继而出现了所谓的模型误差. 为进一步分析T+1交易机制影响,本节还检验了股指期货自身的日夜收益特征以及使用股指期货进行期权对冲的情况.我国股指期货实行T+0交易限制,因此股指期货的日内和隔夜收益特征可能有所不同.这里选取上证50股指期货(IH)和沪深300股指期货(IF)作为对冲工具.由于股指期货采用双向保证金交易,因此PnLb的分母改为ft+|Δt|St×保证金比例(13)为便于计算,统一使用20%作为保证金比例..先看表6,股指期货的隔夜收益都为显著为正,这与期权隐含价格特征相同,与ETF现货价格特征正好相反.这也与张兵[19]发现的我国股指期货隔夜回报为正、隔夜回报为负的结果一致.因此预期使用期货对冲不会出现收益的非对称性.表7的结果证实了本文的猜测,总体上,相较于使用ETF进行对冲,使用股指期货对冲的收益显著性有所下降,但是50ETF.SH和300ETF.SZ期权的隔夜对冲收益仍然显著;并且,从不同期权类型来看,使用股指期货对冲与使用ETF对冲存在明显差异,使用期货对冲的收益并无明显的非对称性,认购和认沽期权的隔夜对冲收益与使用现货对冲的结果完全相反.综上,我国的T+1交易制度是Delta对冲日夜收益的重要影响因素. T+1交易制度导致了ETF资产的日内收益为正、隔夜收益为负的异象以及模型误差,然而投资者又不能及时交易ETF资产,导致套利机会长期存在.即使如此,使用期货进行对冲在总体上仍然存在负的隔夜收益,这说明交易制度并非唯一影响因素.通过以上分析,本文提出以下假设: 表6 股指期货收益的日夜特征 表7 基于期货对冲的Delta对冲收益 假设D标的资产收益日夜反转的强弱反映了T+1交易制度的约束程度.受T+1交易制度影响,标的资产开盘买入的溢价补偿越大,T+1交易制度约束的程度就越深,进而认购和认沽期权的Delta对冲收益的非对称性就越明显. 3.1.5 卖空成本 我国ETF市场的卖空成本相对较高(14)我国50ETF可以当日买入和赎回或者当日申购和卖出,以实现T+0的ETF市场价格和基金净值的套利,然而价格和净值的关系面临不确定性.另外,虽然股票ETF资产纳入了融资融券名单,但是融券交易存在较高的交易成本和持仓限制.,这导致了看跌期权价值更容易被高估而看涨期权价值则容易被低估[29],然而卖空成本和日内、隔夜的关系不大,并不能解释期权对冲日内和隔夜收益的差异.另外,高卖空成本的存在限制了标的市场的卖空行为,投资者难以通过套利交易消除套利空间,导致收益的异象长期存在.由表8可知,在隔夜时段交易(不受T+1限制),买认购期权卖ETF和卖认沽期权卖ETF的策略均可以获取正的收益,然而由于卖空成本的存在,这两种策略均难以执行. 3.1.6 价格压力 由期权卖方或者买方的需求变化导致的期权价格变化统称为“价格压力效应”.Grleanu[9]考察了需求压力对期权价格的影响,发现需求压力会导致不完全的Delta对冲.如果该假设成立,需求压力会直接影响期权本身的收益率,从而影响Delta对冲收益.因此,本节检验了期权自身的收益情况,除了50 ETF.SH期权的隔夜收益为正,其他期权的价格压力效应都不显著.另外,Jones和Shemesh[6]认为期权卖方面临更大的下行风险,因此倾向于收盘前平仓而非持仓过夜,并且这种行为在非交易时间(周末或者节假日)更明显,导致Delta中性组合的回报明显低于交易期间.因此,将样本分为交易时间和非交易时间,分别检验了Delta对冲收益,发现交易时间的结果和前文分析一致,而非交易时间总体上的并结果不显著,且认购和认沽的显著性较弱.因此,Delta对冲收益的异象主要是由交易时间所带来的,非交易时间对结果影响较弱(15)此处省略检验结果,有需要的读者可以向作者索取.. 3.2.1 风险溢价 1)波动率和风险中性峰度为检验实现波动率(假设A)和风险中性峰度(假设B2)如何影响Delta对冲收益,本节构建了回归方程 β3Controlst,dn+εt,dn (10) 表9 Delta对冲收益对波动率和风险中性峰度的回归 从经济意义上分析,隔夜时间是非交易时间,在该时段市场无法通过交易及时反应新的信息,因而面临了较大的不确定性风险.一方面投资者在隔夜时间可能更需要认沽期权进行保险,或者知情交易者在隔夜消息公布以前提前买入期权,愿意支付给期权卖方更高的期权费用;另一方面做市商在隔夜时间也面临更大的对冲风险,需要一定的风险补偿.因此,这些因素叠加可能导致隔夜时间出现了更加明显的波动率风险溢价. 另外,三种期权的风险中性的峰度的日内系数显著为正,隔夜系数基本显著为负(159919期权的隔夜系数不显著).隔夜的回归系数符合理论分析,说明隔夜存在跳跃强度风险的溢价,然而日内正的回归系数均显著为正,这显然不符合日内收益不显著的结果.因此,风险中性峰度的解释能力较弱. 本节还进行了如下稳健性检验:1)Delta绝对值扩大为0.05~0.95(加入深度实值和深度虚值期权数据),结果依然稳健;2)参考Bakshi和Kapadia[1]的分析,检验了标的资产收益率和波动率的相关性关系,发现隔夜的相关性都为负,而日内的大部分为正,这说明隔夜情况符合波动率风险溢价的假设;3)检验了Muravyev和Ni[2]构造的波动率偏差指标,即日内实现波动率除以隔夜实现波动率,结果显示该指标解释力较差,这是因为国内日内Delta对冲收益并非显著为正,因此该检验方法不适用于我国市场(18)此处省略稳健性检验结果,有需要的读者可以向作者索取..综上,假设A成立,假设B2不成立. 2)风险中性偏度 为检验风险中性偏度(假设B1)如何影响Delta对冲收益,本节构建了回归方程 (11) 3.2.2 交易制度 1)模型误差与标的资产收益为检验模型误差与标的资产收益如何影响Delta对冲收益(假设C1、假设C2),本节构建了回归方程 (12) (13) 表11 模型误差与标的资产收益的交互效应 综上,一方面,模型倾向于高估认购期权的对冲比率(模型误差大于0),低估认沽期权的对冲比率(模型误差小于0);另一方面,ETF收益倾向于日内为正,隔夜为负.两者共同作用下,导致了非对称性特征. PnLbt,cp=β1RSt+β2CP+β3RSt× CPD+β4Controlst+εt (14) PnLbt,cp=β1L.RSt+β2CP+β3L.RSt× CP+β4Controlst+εt (15) 回归结果见表12,可以看到结论不变.因此,假设C1和假设C2成立. 表12 期权类型与标的资产收益的交互效应 2)T+1交易制度的约束程度为检验T+1交易制度的约束程度如何影响Delta对冲收益的日夜非对称性(假设D),本节首先考察了期权隐含价格和实际价格的比值ISS(见式(9))和Delta对冲收益的关系,将样本按照ISS由小到大排序,并按照分位数平均分为5组,记为Q1~Q5.图4展示了排序分组后的ISS和对冲收益的关系,从日内来看(图中1列、2列),开盘时ISS越大,认购期权对冲收益越负,认沽期权对冲收益越正,二者差异逐渐扩大.这说明,开盘时刻T+1交易制度的约束程度与认购和认沽期权的非对称正相关.从隔夜来看(图中第3列、第4列),两者关系正好相反,表现为收盘时ISS越小,认购期权对冲收益越正,而认沽期权对冲收益越负.这是因为,开盘时刻标的资产价格相对期权隐含价格越低,收盘时刻就相对越高,即标的资产的日夜反转效应越明显,此时认购和认沽期权的非对称性就越明显. 图4 按ISS分组后的Delta对冲收益 另外,为了更准确的衡量期权隐含价格和实际价格的相对变化的差异,本节还构建了一个新的指标:期权隐含的标的资产收益减去实际标的资产收益(记为DRSS),即 (16) DRSS表示期权隐含的标的资产价格变化相对于实际标的资产价格变化.同样,本节将样本按照DRSS由小到大排序,并按照分位数平均分为5组,记为Q1~Q5.图5展示了排序分组后的DRSS和Delta对冲收益的关系,可以看到无论是日内还是隔夜,均表现出与ISS类似的特征.开盘时刻的DRSS越大,则隔夜的实际标的资产收益率相对越低,意味着日内实际标的资产的收益率相对越高.收盘时刻DRSS越小,则日内实际标的资产收益率相对越高,意味着隔夜实际标的资产的收益率相对越低.最终都加剧了认购和认沽期权的非对称性.为进一步检验上述指标,同时控制住其他因素的影响,本节构建了如下回归 图5 按DRSS分组后的Delta对冲收益 PnLbt,cp,dn=β1ISSt,cp,dn+β2Controlst,cp,dn+ εt,cp,dn (17) PnLbt,cp,dn=β1DRSSt,cp,dn+β2Controlst,cp,dn+ εt,cp,dn (18) 控制变量Controlst包括实现波动率、跳跃风险(包括风险中性下的偏度和峰度)、期权成交量、期权持仓量、到期时间、在值程度和常数项.表13、表14分别展示了回归方程(17)、回归方程(18)的结果.可以看到,在控制了一系列变量以后,两种指标的认购期权系数均为负,认沽期权的系数均为正,这符合单因素分组的结果. 表13 ISS对Delta对冲收益的影响 表14 DRSS对Delta对冲收益的影响 此外,本节还构造了认购期权对冲收益减去认沽期权对冲收益指标,即PnLbt,c,dn-PnLbt,p,dn,作为认购和认沽期权对冲收益非对称性的代理变量,并且用该指标分别对ISS和DRSS回归.由表15可知,在控制了其他变量以后,随着T+1制度约束程度的增加,ISS和DRSS增加,认购和认沽的Delta对冲收益差异越明显.并且,日内回归R方明显大于隔夜的回归,这说明T+1制度约束程度对日内Delta对冲收益的非对称性的解释力较强. 表15 ISS、 DRSS对Delta对冲收益的非对称性的影响 本节还进行了一系列稳健性分析:首先,由于周末效应可能对结果产生影响,因此去除周末和节假日的数据,结论基本稳健.其次,还进行模拟分析,假设存在模型误差,在此基础上检验了不同的标的资产日夜收益对Delta对冲收益的影响,结果符合前文分析(19)此处省略稳健性检验结果,有需要的读者可以向作者索取..综上,假设D成立. 本文对我国股票ETF期权Delta对冲收益的日夜特征进行了研究.研究结果表明,总体上Delta对冲组合的隔夜收益显著为负,日内收益不显著;认沽期权和认购期权的收益存在非对称性,即认购期权的日内收益为负、隔夜收益为正,认沽期权恰好相反.Delta对冲收益异于零的影响因素是多方面的,本文综合考虑了各种可能的影响因素,研究发现总体上波动率风险溢价能够解释隔夜负的Delta对冲收益,但是并不能解释认购和认沽期权的Delta对冲收益的非对称特征;模型误差与标的资产收益的日夜差异能够解释认沽和认购期权Delta对冲收益的非对称性;进一步分析发现,T+1交易制度约束造成了标的资产日夜收益的反转,进而影响到期权对冲收益,T+1交易制度约束程度越大,对冲收益的非对称特征就越明显;最后,T+1交易制度和卖空约束并存导致对冲收益异象长期存在. 本文的发现可以为监管者和投资者带来一定的启发.首先,我国股票ETF市场实行T+1 交易制度,这造成了期权市场交易制度和现货市场交易制度的分歧,不利于市场间的高效联动,一定程度上影响了期权对冲的效率.一方面,T+1交易制度造成了股票ETF日夜收益的反转效应,在存在模型误差的情况下,该效应可能会造成期权对冲误差较大、效率较低.另一方面,T+1交易制度也限制了套利者的日内交易,导致期权和现货定价出现偏差时无法通过套利交易及时消除.在注册制改革的背景下,随着投资者素质提升和各项配套措施的逐渐完善,资本市场的市场化程度也会越来越高.本文的发现为金融监管层未来可能逐步放开T+1制度提供了一定的依据.其次,对于投资者而言,由于模型误差影响了Delta对冲收益,因此投资者可以开发更先进的方法进行期权对冲,例如半参数、非参数或者机器学习的方法,并且充分考虑T+1制度的影响,以尽量规避模型误差风险.总之,本文的研究有助于投资者和监管者更好地理解我国的资本市场,从而提升金融市场定价和对冲效率,更好发挥期权价格发现和风险对冲的功能.未来有两方面研究值得跟进,一是探讨股票市场制度的约束如何影响期权定价,二是将市场制度因素融入期权定价模型.
2 Delta对冲收益的日夜特征
2.1 主要结果
2.2 不同到期时间和在值程度

2.3 基于波动率和标的资产价格关系的Delta
2.4 稳健性检验
3 对冲收益日夜异象的成因
3.1 理论分析与假设
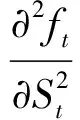




3.2 假设检验
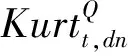




4 结束语

