基于模型平均的中国产出增长和通货膨胀密度预测①

林 娟, 陈海强*, 林 青

(1. 厦门大学经济学院金融系和王亚南经济研究院, 厦门 361005;2. 上海潼骁投资发展中心(有限合伙), 上海 200030)

0 引 言

产出增长和通货膨胀一直是政府部门制定相关经济政策的重要依据[1, 2].对产出增长和通货膨胀展开精准预测有利于政府及时制定有效的宏观经济政策.已有国内外宏观经济预测相关文献大多基于点预测,例如,Stock和Watson[3]基于大型宏观经济数据集评估了多个模型对各国产出增长和通货膨胀的点预测绩效.在国内宏观经济预测方面,陈伟和牛霖琳[4]基于28个解释变量构建了线性预测模型集合,并采用贝叶斯模型平均(BMA)方法对通货膨胀进行预测,发现通胀一阶滞后、工业增加值增速和狭义货币(M1)能够显著预测通胀率.Higgins等[5]基于贝叶斯向量自回归模型(BVAR)预测中国产出增长和通货膨胀,发现广义货币供应量(M2)是关键的预测因子.郑挺国等[6]对我国通货膨胀率进行实时预测,发现“产出—通胀”型菲利普斯曲线在我国并不适用.Sun等[7]使用滚动加权最小二乘法预测中国的经济增长和通货膨胀,发现资产价格是预测产出增长的关键变量.

上述文献研究的点预测仅仅提供了对经济变量未来期望值的预测,并不能全面刻画预测的不确定性.当前国内外形势日趋复杂,中美贸易摩擦叠加新冠疫情全球大流行加大了世界经济发展的不确定性.国内经济也处于转型关键阶段,地方政府债务风险的累积以及局部地区房地产泡沫破灭也加大了我国宏观经济运行的风险.因此,如何考虑上述不确定性带来的影响是宏观经济预测面临的重要问题.

与点预测不同,密度预测是对经济变量的未来条件概率分布进行预测,能有效地刻画预测的不确定性.事实上,近年来密度预测越来越受到各国中央银行和国际组织的重视,其中扇形图(fan chart)作为最常用的直观展示密度预测结果的形式在业界得到广泛使用.例如,英国中央银行自1997年开始定期在《通货膨胀报告》(inflation report)中以扇形图的形式公布对GDP增长、CPI通货膨胀和失业率等指标的密度预测结果.同时,该报告也以表格的形式展示了对这些宏观经济变量在10、25、50、75和90百分位(percentile)下的预测.在这之后,欧洲中央银行、日本中央银行、瑞士中央银行、挪威中央银行和美联储等纷纷以扇形图的形式公布对主要宏观经济变量的密度预测结果.从2006年4月开始,国际货币基金组织开始在《世界经济展望》中以扇形图的形式公布对世界GDP增长前景的密度预测结果,该图形直观地显示了《世界经济展望》核心预测在50%、70%和90%置信区间上的不确定性.Yu[8]基于北大CCER的“朗润预测”对中国GDP进行密度预测并绘制扇形图,发现扇形图能够有效地刻画经济不确定性和经济风险水平.

与点预测类似,不同的模型设定和预测变量选择亦可能产生不同的密度预测,因此需要对不同密度预测模型进行评估.然而,类似均方根预测误差(RMSE)等传统预测比较方法不再适用于评判密度预测的优劣,因此文献中往往通过统计检验的方式来分析该密度预测模型是否能够有效近似被预测变量的分布函数.Diebold等[9]首次证明检验密度预测模型的设定正确与否等价于检验概率积分变换(PIT)序列是否服从[0,1]区间的独立均匀分布.针对这个双重假设检验问题,Diebold等[9]使用直方图检验PIT序列是否服从U[0,1]分布,使用自相关图检验PIT序列是否具有独立性.继Diebold等[9]的开创性论文后,检验PIT序列是否服从[0,1]区间上的独立均匀分布成为了评估密度预测模型的主流方法.Bai[10]提出了基于Kolmogorov检验的非参数方法.该方法在假定PIT序列独立的前提下,仅仅对均匀分布性质进行检验.Hong等[11]提出了非参数检验统计量同时检验PIT序列的独立性和均匀分布假设.Lin和Wu[12]提出了基于Copula方法的序贯检验法,分步检验独立性和均匀分布假设.Rossi和Sekhposyan[13]在检验原假设中考虑了模型的参数估计误差.上述密度预测评估方法被广泛应用于宏观经济实证研究.例如,Rossi和Sekhposyan[14]比较了大量的基于正态假定的宏观经济预测模型对美国产出增长和通货膨胀的密度预测绩效.Hong等[15]考察了各种利率模型对中国7天回购利率的样本内拟合绩效.

本文使用资产价格、实体经济、工资物价以及货币等17个变量预测中国的产出增长和通货膨胀.参照Stock和Waston[3],将上述17个预测因子单独或联合加入预测模型构建密度预测模型集合,并在这些模型基础上通过加权平均方法得到加权密度预测.此外,本文运用Diebold等[9]提出的模型设定检验方法对各预测模型进行可适性检验.本文主要发现如下:第一,仅基于产出增长和通货膨胀自身滞后期构建的AR模型无法通过所有的统计检验,因此有必要在预测模型中引入其他预测因子.第二,在预测产出增长时,货币供给是影响我国产出增长未来分布的重要因素.而在预测通货膨胀时,银行同业拆借市场1天加权平均利率、人民币名义有效汇率指数、商品房销售均价以及货币供给均是影响我国通货膨胀未来分布的重要因素.第三,基于正态假设的单个ADL模型大多存在着模型误设的问题,无法通过可适性检验,然而对多个ADL模型进行加权平均后能够显著降低模型误设风险,与汪寿阳等[16]结论一致.最后,基于最小二乘法(OLS)估计的贝叶斯模型平均(BMA-OLS)方法通过了所有的模型设定检验,可以用来预测中国产出增长和通货膨胀的未来分布.本研究对于政策制定部门开展宏观经济预测监控,制定精细化、精准化宏观经济调控措施提供了参考依据和方法支撑.

1 密度预测评估方法

假定{Yt}是一个宏观经济时间序列,例如产出增长或通货膨胀.本文关注在t时刻对{Yt}的真实条件密度函数进行预测.假设存在参数化的密度预测模型(ft+h(y|Ωt,θ0),其中θ0是有限维的未知参数,Ωt是在t时刻的可用信息集.定义ft+h(y|Ωt,θ0)对应的概率积分变换(PIT)序列

t=R+1,…,T-h

(1)

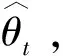
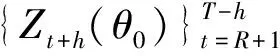
(2)

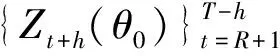
原假设(2)是一个联合检验问题,需要同时检验PIT序列的独立性以及[0,1]区间上的同均匀分布性质.如果PIT序列的独立性假设被拒绝,说明密度预测模型错误地捕捉了序列中的动态信息;如果PIT序列服从均匀分布的假设被拒绝,说明密度预测模型可能错误地捕捉了边缘分布的信息,或者可能错误地捕捉了序列中的动态信息,或者可能同时错误地捕捉了这两方面的信息.如果PIT序列的同分布假设被拒绝,说明密度预测模型错误地捕捉了数据中的结构性变化特征.

针对原假设(2),文献中有两类常用的检验方法:直接检验法和逆正态变换检验法.

1.1 直接检验法

这类方法直接检验PIT序列{Zt+h(θ0)}是否服从[0,1]区间上的独立同均匀分布.本文将运用下面的检验统计量分别检验PIT序列的均匀分布性质、独立性和同分布性质.

1)均匀分布检验

(3)

(4)

2)独立性检验

使用Ljung-Box(LB)统计量检验原假设:PIT序列的一阶和二阶中心矩不存在序列相关.LB统计量的计算公式如下

(5)

3)同分布检验

(6)

(7)

Andrews[17]结构断点检验的基本思想是在结构断点T1可能出现的区间[t1,t2]内,遍历所有时点,逐个计算Wald统计检验量W(T1),本文定义t1=[0.15P],t2=[0.85P],[·]表示取整,P为样本外预测的总长度.在此基础上,计算最大Wald检验统计量

SupW=supT1W(T1)

(8)

如果检验结果拒绝了原假设,则判断存在结构性变化,并取最大Wald统计检验量对应的时点定义为结构断点.采用遍历的方法避免了Chow检验需要事先设定断点位置而可能造成的对结构性变化位置的误判.

1.2 逆正态变换检验法

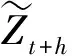
1)Berkowitz[18]检验

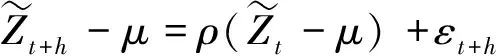
(9)

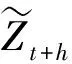
2)Doornik和Hansen[19]检验(DH检验)

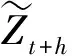
2 宏观经济密度预测模型

首先介绍自回归分布滞后(ADL)模型,然后再介绍基于多个ADL模型进行加权平均得到的组合预测模型(pooled model).

2.1 自回归分布滞后模型

令Xt={Xt1,...,XtK}表示K个预测变量集.本文考虑了资产价格、实体经济、工资物价以及货币等17个关键指标,具体定义和计算方法见后文.单一预测因子的ADL模型具体形式描述如下

Yt+h=αk0+αk1(L)Xtk+αk2(L)Yt+ut+h,k

(10)

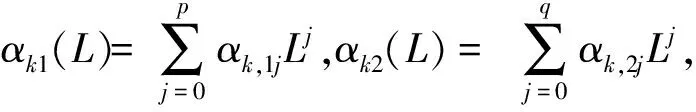
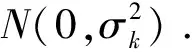
(11)

注意简单自回归模型(AR)是ADL模型的一个特例,即只使用因变量的滞后项来预测产出增长和通货膨胀,沿用式(11)中的符号,AR模型在t+h时刻的概率积分变换为

(12)

在单因子预测模型(10)的基础上,还考虑了基于多因子的ADL模型,具体形式如下

(13)

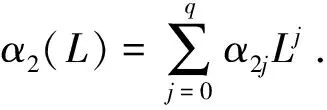
2.2 组合预测模型

组合预测模型通过对多个子模型赋予适当的权重进行加权平均构建新的模型,能够改善预测绩效[21].在权重的选取上,考虑等权重和变权重两种不同的方法.在子模型的选取上,既考虑了单因子模型,又考虑了多因子模型.值得指出的是,虽然假定单个模型的残差项ut+h,k服从正态分布,但组合密度预测模型将服从混合正态分布.随着子模型个数的增加,组合密度预测模型的灵活性增加,能较好地刻画数据中可能存在的厚尾特征.由于本文使用的是线性组合模型,先对单个条件密度预测模型进行组合,再计算组合预测模型的PIT,和先计算单个条件密度预测模型的PIT再对PIT序列进行组合,两者是等价的.为了简单起见,先计算单个预测模型的PIT序列,而后对各PIT序列进行加权.

1)简单平均模型(SAM)

Stock和Watson[3, 22]证明了简单平均的组合预测模型在点预测中具有较好的预测效果.本文将这一思路拓展到密度预测的框架中.首先估计K个单因子ADL模型并计算各模型对应的PIT序列,再对各序列赋予相等的权重(1/K).SAM的概率积分变换定义如下

(14)

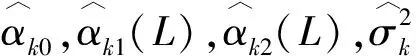
2)贝叶斯模型平均(BMA)

①基于OLS参数估计的贝叶斯模型平均(BMA-OLS)

BMA-OLS模型使用OLS方法估计ADL模型中的参数.在计算出各ADL模型对应的PIT序列后,使用模型的后验概率作为权重对各序列进行加权平均.相应的概率积分变换如下

(15)

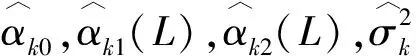
②完全贝叶斯模型平均(BMA-Full)

BMA-Full模型使用贝叶斯方法估计模型的参数,并使用模型的后验概率作为权重对各PIT序列进行加权平均.BMA-Full的概率积分变换为

(16)

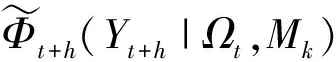
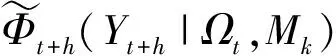
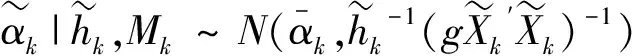
(17)

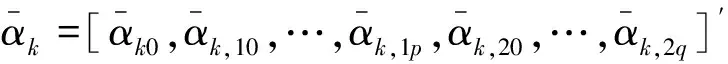
(18)

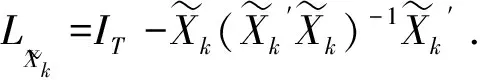
(19)

其中

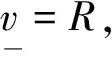
(20)

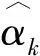
(21)

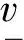
假设所有单一模型都拥有相同的先验概率.通过贝叶斯公式可以得到模型的后验概率

(22)

和边际似然值

(23)

其中∝表示成比例.

③BMA-MC3模型

BMA-MC3(Markov Chain Monte Carlo Model Composition)模型和BMA-Full模型都采用贝叶斯方法估计模型的参数.两者的不同之处在于,BMA-Full模型是对包含单一预测因子的ADL模型进行加权平均.而BMA-MC3模型则允许将k个解释变量同时加入回归模型中,k=1,…,K.在单一模型是线性模型的假定下,当解释变量的个数是K时,模型空间中的模型总数达到2K,因而,遍历模型空间中的所有模型是不可行的.BMA-MC3模型采用马尔科夫蒙特卡洛模型综合算法对模型进行抽取.具体算法如下:

第一步:将初始模型记为M0.初始模型中除了包括被解释变量的q阶滞后项外,还包括了一个解释变量.

第二步:在第s次抽签中,s=1,…,S,以相同的概率从下面的模型中随机抽取备选模型M*:a)当前的模型M(s-1);b)从当前模型M(s-1)中删除一个解释变量得到的新模型;c)增加一个解释变量到当前模型M(s-1)中得到的新模型.备选模型生成后,依据如下的接受概率判断是否接受备选模型

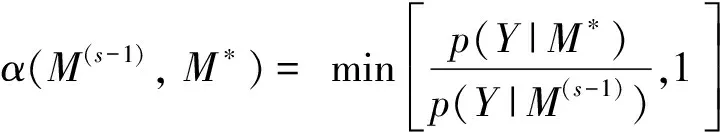
(24)

其中p(Y|M(s-1))和p(Y|M*)由式(23)计算得到.如果备选模型被接受,M(s)=M*;如果备选模型不被接受,M(s)=M(s-1).

MC3算法倾向于抽取后验概率较高的模型.当抽取次数足够多时,MC3算法能够确保抽取的模型趋近于真实模型.

BMA-MC3模型的概率积分变换可以表示为

(25)

3 数据及变量选取

本文旨在估计产出增长和通货膨胀的预期条件密度分布,参考Rossi和Sekhposyan[14],将产出增长和通货膨胀分别使用经季节调整后的实际GDP和GDP平减指数的环比折年率计算得到,具体计算公式为

GDP_growtht+h=(400/h)ln(RGDPt+h/RGDPt)

(26)

Inflationt+h=(400/h)ln(PGDPt+h/PGDPt)

(27)

其中RGDP和PGDP分别表示实际GDP和GDP平减指数.当h=1时,该预测为季度预测,即将季度环比增长率折算为年度增长率,而当h=4时,该预测为基于季度同比增长率的预测.当经济处于大幅波动时期,相较于同比增速,环比折年率更具有时效性,能够更好地捕捉经济的拐点,从而有助于政策制定者了解宏观经济的短期走势.图1描绘了1999年第1季度～2019年第2季度经季节调整后的中国实际GDP和产出增长走势图.图2描绘了同时期中国GDP平减指数和通货膨胀走势图.从图中可以看出,实际GDP和GDP平减指数均呈明显上升趋势.此外,产出增长和通货膨胀在2008年金融危机期间均出现大幅波动.参照Stock和Waston[3],考虑资产价格、实体经济、工资物价以及货币等方面的17个关键指标(见表1).代表资产价格的指标包括利率、股指、汇率和商品房价格.其中,利率指标选取了反映短期资金面需求的指标(银行同业拆借市场1天加权平均利率)和反映期限结构的指标(由中债公司编制的不同期限国债到期收益率).除了反映资金成本的利率指标外,股票价格也是资产价格的重要组成,本文选取上证综合指数作为股票资产价格的指标.汇率指标反映了一国资本价格相对于外国的变化情况,是开放经济体资本价格的重要影响因素.本文选取人民币名义有效汇率指数作为汇率指标.住房制度改革后,房地产市场的价格波动与我国经济和物价等宏观变量高度相关,本文选取了商品房销售均价(销售额/销售面积)作为房价指标.

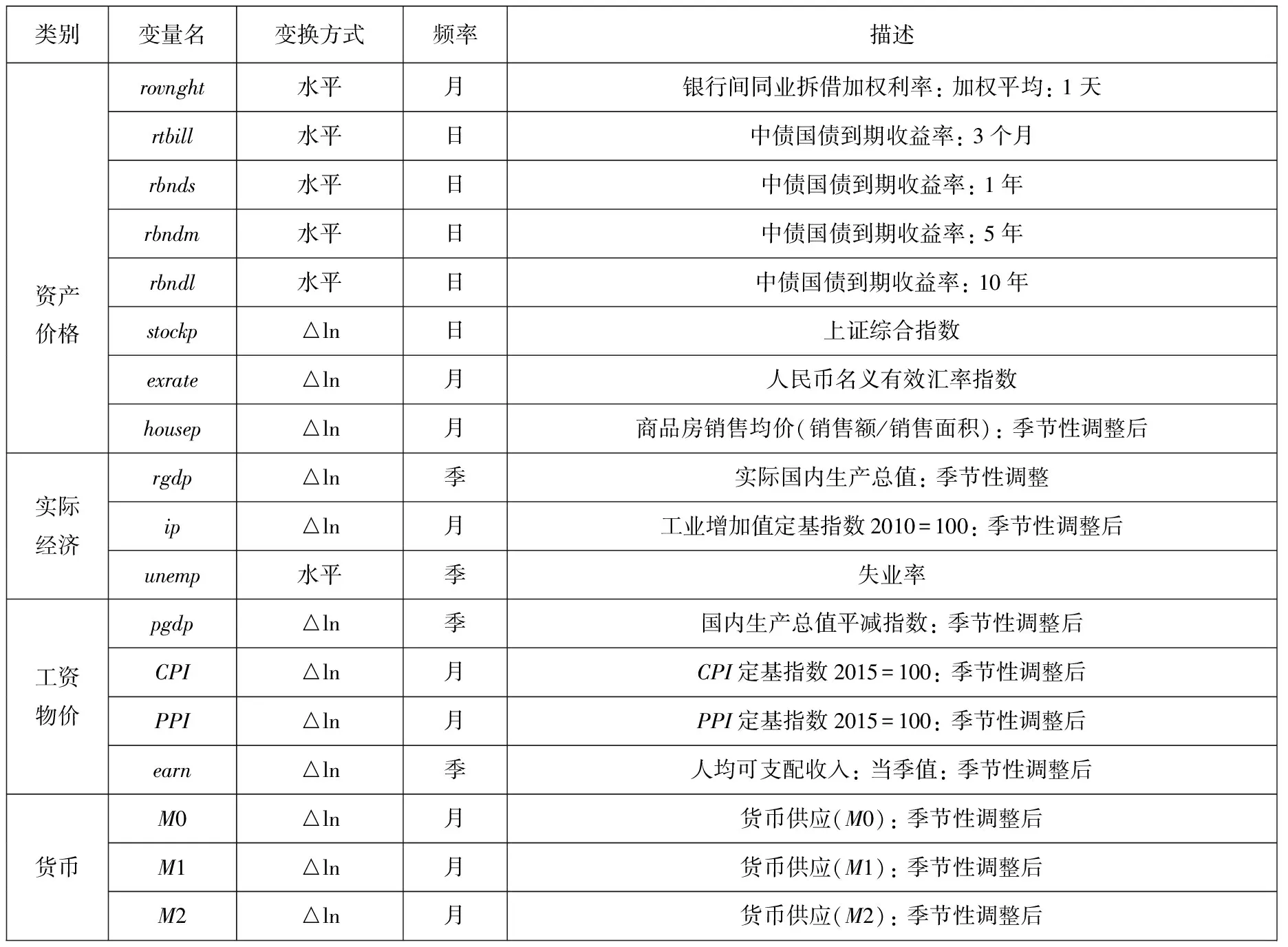
表1 宏观经济数据集描述

图1 实际国内生产总值和产出增长

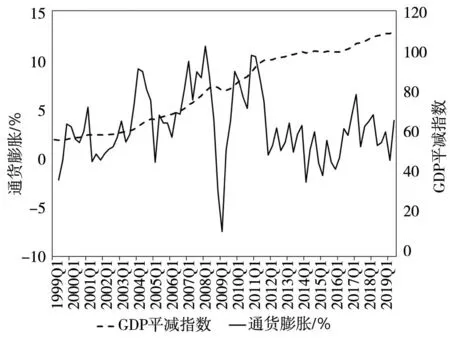
图2 GDP平减指数和通货膨胀

代表实体经济的指标包括实际GDP,工业增加值以及失业率.实际GDP由GDP现价值剔除了通货膨胀的影响后得到.工业增加值反映了工业生产增减变动.失业率反映了宏观经济运行状况和劳动力市场景气程度.代表工资和物价的指标包括GDP平减指数、居民消费价格指数(CPI)、生产者价格指数(PPI)和人均可支配收入.贺力平等[25]指出,消费者价格指数更多地反映消费需求因素,而生产者价格指数较多地反映工业原料供给因素.人均可支配收入反映了居民总体可支配收入.货币指标包括了流通中的货币(M0)、狭义货币(M1)和广义货币(M2).它们都是反映货币供应量的重要指标.

本文所有指标的原始数据都来源于WIND宏观经济数据库和CEIC中国经济数据库.为了剔除数据序列中随机性、确定性趋势和季节性的影响,参照Stock和Waston[3]对数据进行转换.如果原始数据是百分比形式,对数据不做特别处理,变换方式标记为“水平”.如果原始数据不是百分比形式,对数据做对数差分处理,变换方式标记为“△ln”.处理后的所有数据都保持百分数形式,所有增长率都是年化后的数据.对于存在季节性变动特征的序列,采用国际通用的X-11ARIMA的方法对其进行季节性调整.由于定基指数的基期定期更换,借鉴杨子晖[26]和杨子晖等[27],采用同比指数将其转换为同一基期的定基指数.由于各指标可获取数据长度的限制,该数据集涵盖的样本区间从1999年1月～2019年6月,并且以1993年第1季度～1998年第4季度的产出增长和通货膨胀作为先验样本数据.数据的起始和终止时间是由数据的可获得性决定.此外,出于数据频率一致性的考虑,对于频率为“日”的数据序列,使用月度内日平均值作为月度变量值.对于月频数据,参照Stock和Waston[3]的处理方式,对工业增加值和CPI的月度数据求平均值计算季度数据.针对其他变量,使用3月、 6月、 9月和12月的最后一个观测值作为季度数据.最终使用季度数据进行分析.

4 实证结果

4.1 密度预测模型评估结果

由于数据长度限制,本文只考虑一步密度预测(2)根据第2部分的论述,当h=4,在进行假设检验时需要将全样本分成4个子样本,每个子样本序列的时间间隔为4.通过分别检验每个子样本序列是否是独立且同服从[0,1]区间上的均匀分布,以判别条件密度预测模型的设定是否正确.然而若将文中的样本数除以4,每个子样本中只有20个数据点,样本量太少,鉴于此,只讨论一步预测.但本文提出的方法可以应用于h=4对应的年度预测.,即h=1.借鉴Rossi和Sekhposyan[14]和Mandalinci[28],使用滚动预测窗口方法,滚动窗口设置为R=40.表2给出了对AR模型和17个ADL模型进行统计检验得到的经验p值.使用的检验方法包括:直接检验法中的均匀分布检验(KS检验和AD检验)、独立性检验(基于一阶中心矩和二阶中心矩的LB检验)、同分布检验(基于一阶非中心矩和二阶非中心矩的QLR检验)和逆正态变换检验法(Berkowitz检验和Doornik和Hansen检验).“AR”行报告的是对AR模型进行统计检验得到的经验p值.加粗的“ADL”行报告的是通过特定假设检验的ADL模型个数占模型总个数(17个)的比重.

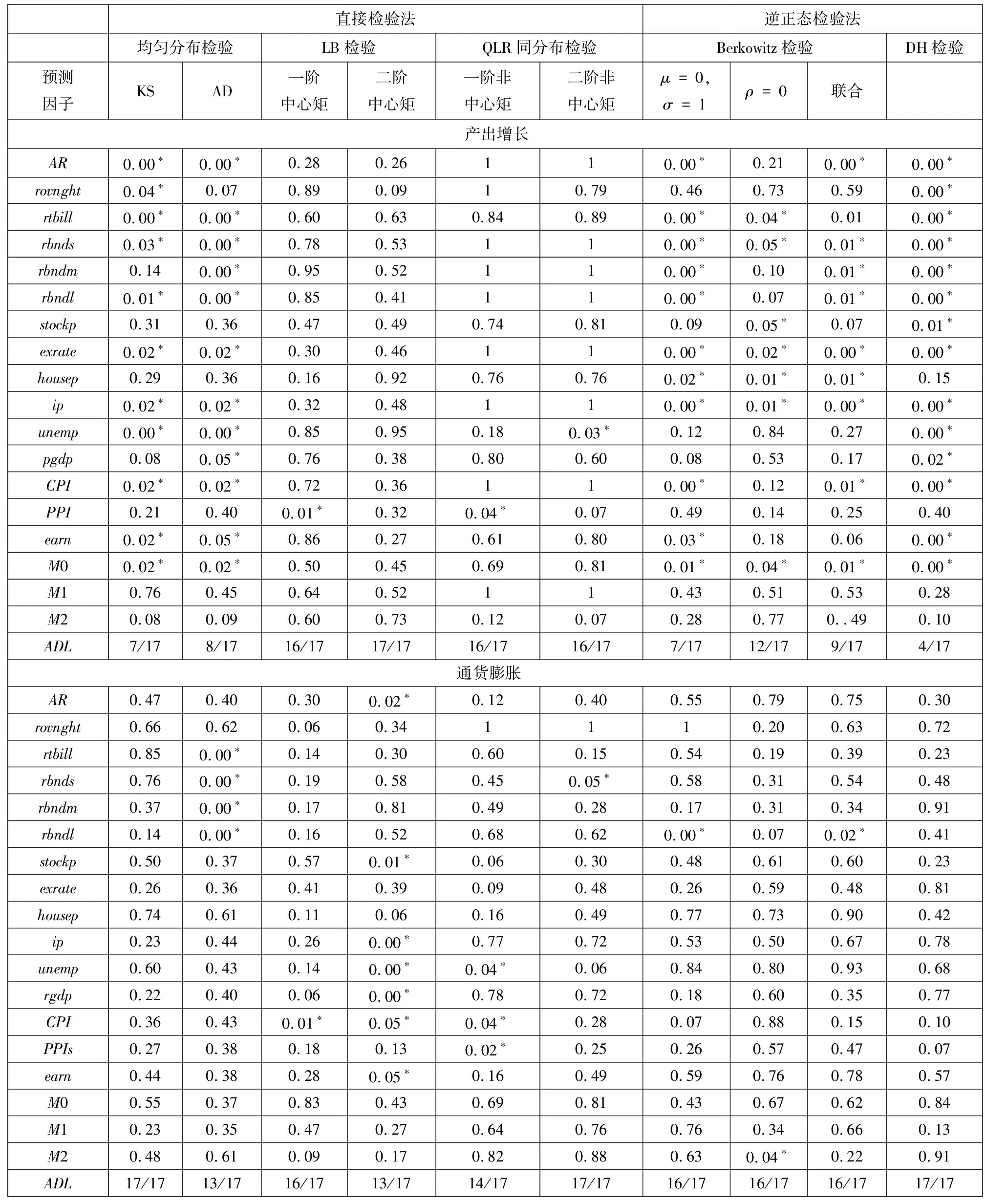
表2 基于AR模型和单一因子的ADL模型的检验结果汇总

表3汇总了对组合预测模型进行统计检验得到的经验p值.

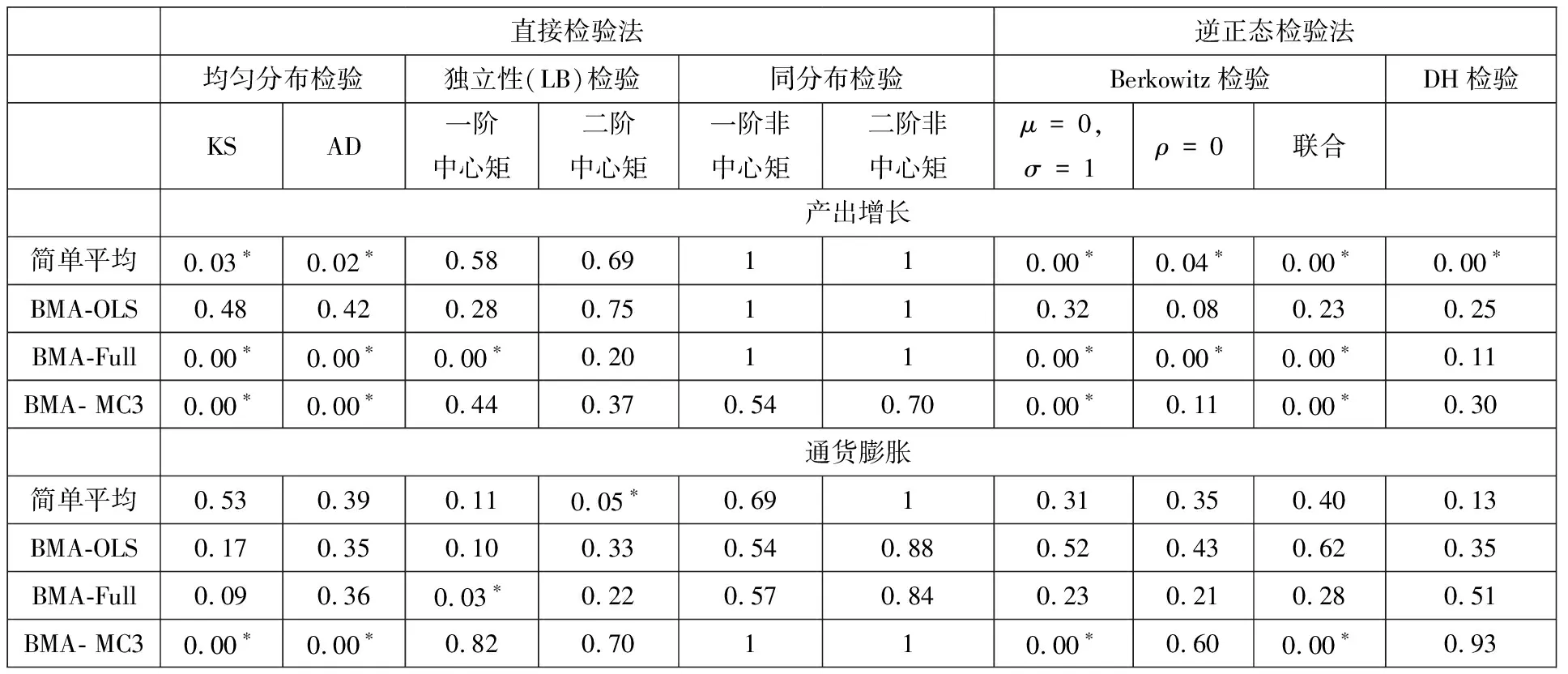
表3 组合预测模型检验结果汇总

从表2和表3的结果可以看出,在针对产出增长的预测中,以M1和M2为预测因子的ADL模型和BMA-OLS模型在95%的置信水平上通过了所有的检验.而在通货膨胀密度预测中,以rovnght、exrate、housep、M0和M1为预测因子的ADL模型和BMA-OLS模型在95%的置信水平上通过了所有的检验.借鉴Rossi和Sekhposyan[14],如果某个预测模型通过了所有的统计检验,则认为该模型设定是基本正确的.虽然某些包含单一预测因子的ADL模型也通过了所有的模型检验,但是为了避免实证研究中预测因子选择所带来的困难,在下面的分析中仅关注BMA-OLS组合预测模型.

4.2 产出增长和通货膨胀的密度预测结果

在这一部分中,将基于4.1节的模型检验结果,使用10年滚动窗口估计方法对产出增长和通货膨胀进行样本外一步预测.初始滚动窗口选择为1999年第3季度～2009年第2季度.

图3描绘了2009年第3季度～2019年第2季度间中国产出增长的真实值(黑色实线),以及基于BMA-OLS密度预测模型得到的第95百分位数(95 percentile, 虚线)和第5百分位数(5 percentile, 虚点线)预测结果.为了方便比较,图中也描绘了点预测结果(点线).从图3中可以看出,除了2017年第3季度和2019年第1季度外,真实值均处于预测的第95百分位数和第5百分位数的预测区间之内.BMA-OLS模型较好地捕捉了产出增长预测中的不确定性.

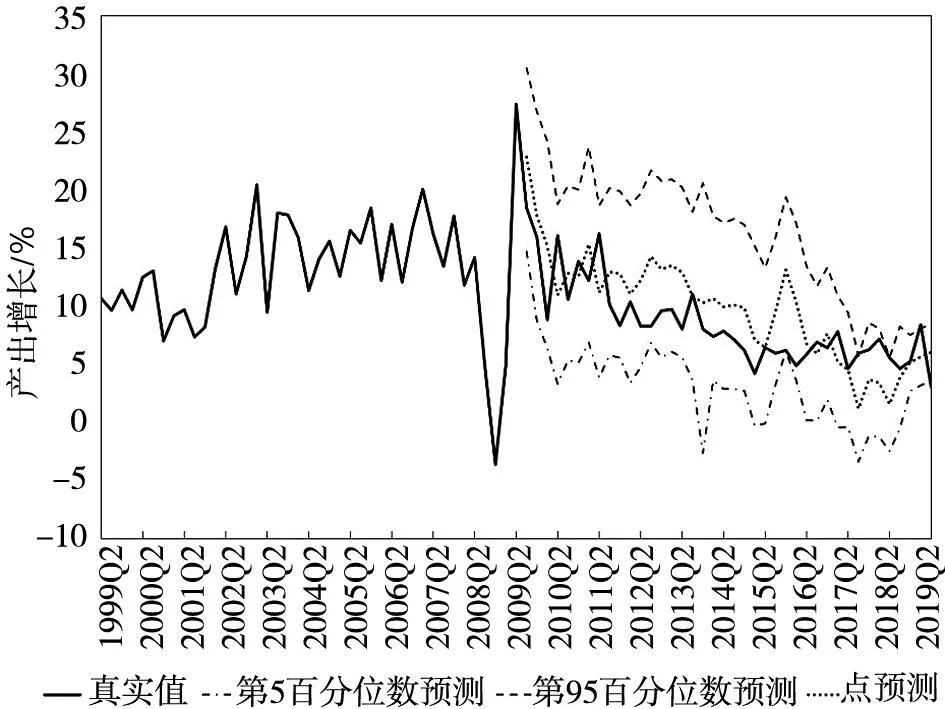
图3 基于BMA-OLS模型的中国产出增长预测

图4描绘了2009年第3季度～2019年第2季度间通货膨胀的真实值(黑色实线),以及基于BMA-OLS密度预测模型得到的第95百分位数(虚线)和第5百分位数(虚点线)预测值.为了方便比较,图中也描绘了点预测结果(点线).从图中可以看出,除了2010年第4季度、2013年第2季度和2019年第2季度外,真实值均处于第95百分位数和第5百分位数的预测区间之内.BMA-OLS模型较好地捕捉了通货膨胀预测中的不确定性.

图4 基于BMA-OLS模型的中国通货膨胀预测

5 结束语

现有宏观经济变量的预测文献大多基于点预测,然而点预测仅仅对宏观经济变量的条件均值做出预测,在不确定性因素明显增多的国内外新形势下,往往不能完全满足政策制定的需要.据此,本文基于大量宏观经济预测因子构建了中国产出增长和通货膨胀的密度预测模型集合,并利用Diebold等[9]提出的检验方法评估各密度预测模型的可适性.为降低模型不确定性带来的风险,本文使用组合预测模型方法,并最终基于可适用的BMA-OLS组合密度预测模型,得到我国产出增长和通货膨胀的密度预测.

本文主要结论可概括如下:第一,基于产出增长和通货膨胀自身滞后期构建的AR模型无法通过所有的统计检验,因此有必要在预测模型中引入其他的预测因子.第二,在预测产出增长时,本文发现货币供给是影响我国产出增长未来分布的重要因素.而在预测通货膨胀时,本文发现银行同业拆借市场1天加权平均利率、人民币名义有效汇率指数、商品房销售均价、M0或M1均是影响我国通货膨胀未来分布的重要因素.第三,组合预测方法显著地降低了模型设定误差,在产出增长和通货膨胀的密度预测中具有明显的优势.

本文政策建议如下:首先,中国央行可以遵循国际惯例,对中国主要宏观经济变量进行密度预测,并基于密度预测结果定期公布主要宏观经济变量的扇形图,以展示中国经济前景面临的不确定性.其次,货币供给是影响中国产出增长未来分布的重要因素.政府部门在进行稳增长调控时应充分发挥货币政策工具的作用.最后,利率、汇率、房地产价格和货币供给都是影响中国通货膨胀未来分布的关键因素.央行在稳定物价、稳定通货膨胀预期时应综合考虑货币供给、利率水平、汇率因素和资产价格等多方面因素.