基于改进分层博弈交叉效率模型的政策评价①

王兆华, 李靖云, 王 博*, 张 斌

(1. 北京理工大学管理与经济学院, 北京 100081; 2. 数字经济与政策智能工业和信息化部重点实验室, 北京 100081)

0 引 言

政策效果评估作为政策过程中的关键环节,是检验公共政策质量和水平的基本途径,也是实现公共资源合理、有效配置的重要依据.在能源与环境领域,如何提升能源资源利用效率是促进经济、社会与生态环境协调发展的基本问题.政策的出台所导致的政策前后的能源与资源利用效率评价成为重要研究议题,该问题的探讨对于助力我国“碳达峰”与“碳中和”目标的实现具有重要意义.

数据包络分析方法[1-5]在1978年被Charnes等[6]提出,简称DEA模型,它解决了决策单元多投入产出的相对效率评价问题,得到了各领域学者与产业界的广泛应用[7-18].近年来,学者们围绕决策单元竞争与合作关系的动态变化以及决策单元最优权重偏好设定问题,对传统DEA方法进行了一系列改进.在决策单元竞合关系方面,传统DEA方法将每个决策单元看作独立的评价体系,并没有考虑主体之间的交互影响.围绕决策单元间的竞合关系,学者们对传统的DEA分析方法进行不断地改进和完善.其中,交叉效率理论考虑各方主体的评价,从全局考量最优决策单元,解决了传统评价方法中权重仅仅依赖目标单元而设定的问题,由于综合考虑多个目标单元的优势,改进的交叉DEA方法被广泛地应用于评价决策问题[19-22].该模型在计算交叉效率的过程中,并没有将合作博弈情形充分纳入分析框架,因而无法考虑主体间存在竞争关系的效率评价.基于此,Liang等[23]将博弈理论与交叉效率相结合,提出了博弈交叉DEA,对交叉效率做了进一步的改进,有效地解决了上述问题.随后,该方法被广泛的应用于解决成本和资源分配、碳配额分配以及节能减排潜力等领域[24-28].

在现实世界中,主体之间的博弈是复杂的,现有的博弈交叉效率对于决策单元间关系的考量要么是竞争关系、要么是合作关系,同时考量竞争与合作动态关系变化的模型极其匮乏[29].尽管有不少学者探讨了主体的竞争与合作关系并存的状态,如竞合交叉效率DEA[30],然而这些方法并未同时从时间和空间维度上考虑竞合关系,也并未考虑现实外界冲击对竞合关系的影响.实际情况中,决策单元间竞争与合作关系经常同时存在,同时,决策单元间竞合关系也并非一成不变,如在受到试点政策等外界冲击后会发生明显或微妙的变化,进而引起效率的变动.为此,将合作与竞争关系动态演化纳入效率评价的分析框架具有重要意义.在合作与竞争过程中,决策单元为了得到更高的交叉效率会选择结盟,而联盟外的单元由于存在着竞争会导致较低的交叉效率.如果每个决策单元都选择竞争,那么决策单元都将会得到最小交叉效率;如果都选择合作形成一个大联盟,那么决策单元都将得到最大交叉效率.现实情况往往是决策单元间形成不同的联盟且联盟之间存在着竞争.

在决策单元最优权重偏好设定问题上,传统DEA确定评价效率值时,采用最有利于评价单元的取值原则,容易夸大决策单元长处、回避缺陷.针对这一问题,学者们对交叉效率矩阵进行了深入的分析和整合,并进一步改进了传统的平均交叉效率得分.Chen和Wang[31]讨论了决策者偏好对交叉效率的影响,解决了传统DEA在目标设置方面的局限性;Kao和Liu[32]基于松弛的测量方法来计算交叉效率,避免了传统交叉效率的一些缺陷;Wu等[33]和Giannis[34]利用信息熵对交叉效率矩阵进行了加权平均.传统交叉效率具有综合考虑各主体之间的相互评价的优势,结果体现一定的公平性.然而,在交叉效率评价过程中,决策单元虽然同时考虑了自身和其他决策单元的最优权重,但计算最终效率时对自评的考量不充分,自评的过分稀释导致了自评的价值不能充分体现,引起评价的公平问题.基于此,本文从公平角度出发,提出公平博弈交叉DEA算法,对所有的他评取均值作为他评的综合数值,然后再分配自评和综合他评的比例,解决自评过度稀释的问题.

为此,本文首先构建分层博弈交叉效率评价方法,实施二次目标模型构建多层次效率矩阵,充分考虑试点政策前后主体间合作与竞争关系变化,放松传统评价模型竞争性假设.其次,在公平视角下,修正传统交叉模型自评和他评的占比,弥补了传统交叉效率模型对自评的过分稀释的问题,并在公平的分配原则下,利用Shapley值对效率进行综合的评价.最后,以水权交易市场为例,通过比较竞合关系演变所带来的效率差异,验证了水权交易市场政策的有效性和外溢性,为能源与环境领域试点政策效果评价提供了可行方法.

1 分层博弈交叉效率算法

1.1 考虑公平的交叉效率评价模型

数据包络分析(DEA)在处理多投入多产出情况的效率评价具有明显的优势,该模型避免了函数形式的假设,具有客观性,并且易于变形,可进行其他形式的扩展[35, 36].具体的一般形式如下所示

urk,vik≥0,r=1,2,…,s,

i=1,2,…,m

(1)

在交叉效率值的计算过程中,各主体都是尽可能地使得自己的效率得分最大,而不考虑是否会降低其他主体的效率值.其实,在现实的过程中,各主体间存在着竞争和合作的关系,那么有必要进行更深层次的效率值的探究.主体k的最优效率值为Ekk,则其他主体在主体k效率值不降低的前提下,最大化自身的效率,即寻找各自最优权重.具体模型如下所示

urk,vik≥0,r=1,2,…,s,i=1,2,…,m

(2)

传统交叉效率模型在求解交叉效率时,自评的效率值只占交叉效率的1/n,本文对交叉效率的求解过程进行了改进,先对所有的他评取均值作为他评的综合数值,称为综合他评,然后,再分配自评和综合他评的比例.本文中自评和综合他评各占50%,具体的求解如下所示

(3)

(4)

(5)

1.2 公平原则下Shapley值的效率方法

定义1N={1,2,…,n}表示n个主体组成的集合,对于任一子集A⊂N,定义A的特征函数为

(6)

其中

(7)

各决策单元在合作博弈(N,F)的收益可以根据Shapely值进行分配,具体公式如下

[F(A)-F(A-{k})]

(8)

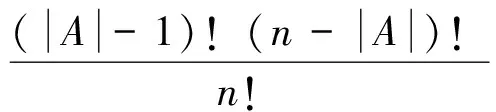
对于定义1中的合作博弈(N,F),主体k(k∈{1,2,…,n})的Shapley值为

(9)

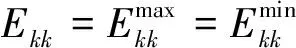
证明对于DMUk,假设k∈A,由定义1可知

(10)

(11)

则DMUk在A中的贡献为

(12)

由式(7)定义可得,当j∈A-{k}时

(13)

将式(7)、式(13)代入式(12)可得

(14)

将式(14)代入到式(8)

(15)

设a,bj,cj满足下列等式

(16)

进一步可知

(17)

进一步可知

(18)

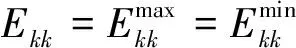
1.3 考虑竞合关系动态演化的分层博弈DEA

试点政策评价问题是政策研究领域的重要课题之一,试点政策的实施通常会引起主体间竞合关系发生变化,进而引致效率的变化.政策实施前,主体之间的竞争与合作关系是不确定的,各地区可以根据自身效率判断与最优资源配置的差距,制定策略提高资源配置效率.因此,从效率的角度来看,每个主体都具有结盟的动力,以便获得更高的评价[37].

政策实施后,主体之间的合作与竞争关系由于试点地区的政绩比拼和政策考核而发生变化.试点地区内部由于存在交易约束,其效率会因为合理分配而得到较高的评价,形成新的联盟,试点地区内部的相互评价趋于最大,而对其他地区的评价趋于最小.非试点地区内部合作与竞争关系共存,利用Shapley值综合考虑非试点地区内部自评和他评.非试点地区和试点地区之间存在着政绩竞争,相关交易无法在其中流转,非试点地区对试点地区的评价较复杂.试点地区和非试点地区的博弈情况如表1所示,每个地区都有两个策略,分别是对其他地区高的效率评价和低的效率评价,V(Z)表示非试点地区A和试点地区B选择策略后的收益,该收益通过效率和排名两个特性表示.

表1 试点地区与非试点地区博弈情况

定义收益函数V,具体形式如下所示

(19)

Zi=(Xnew-Xlow)×(Ynew-Ylow),X表示决策单元排名,Y表示效率值,new和low分别代表其他决策单元对被评价单元的任何评价和低评价,Xnew表示其他决策单元选择任何策略时被评价单元的排名,Xlow表示其他决策单元选择低评价时被评价单元的排名,同上,Ynew和Ylow代表其他决策单元选择策略时被评价单元的效率值.

传统的博弈交叉效率基于非合作博弈视角,没有充分考虑主体间竞合关系的动态变化.改进后该方法考虑了政策对竞合关系的冲击,并测度了竞合关系变化所引致的效率变化,可以通过竞合关系演变所导致的效率差异评价政策的有效性.

2 模型的实证分析

本文以水权交易市场为例验证改进分层博弈交叉效率模型的可行性,比较了竞合关系的动态演变带来的效率差异,进而验证水权交易市场的有效性.目前,国际社会有很多成功的案例已经肯定了水权市场的积极作用[18, 38-40],然而我国的水权交易仍处于初级阶段.评价大多从时间维度上进行前后对比,而忽略了技术进步等因素的影响,不能准确识别政策效果.相比于传统的博弈交叉模型,本文考虑了多主体博弈及政策所引致的竞合关系的演变,在多主体博弈效率评价方面具有明显的优势.

2.1 数据

考虑到影响水资源利用效率的关键因素与数据的可获得性,本文选取省级效率评价数据开展模型的实证分析.投入指标包括:资本存量(亿元),劳动力(万人),总用水量(亿m3),其中各省资本存量计算方法为永续盘存法[41],劳动力为各地区年末就业人数,总用水量包括了农业用水、工业用水、生活用水和生态用水;产出指标包括:地区生产总值(亿元),废水排放量(万吨),其中各地区废水排放量包括了工业废水、生活废水等.除水资源利用效率值,其余数据均来源于《中国统计年鉴》、各省统计年鉴以及各地区历年的水资源公报.各省生产总值、资本存量以2000年为不变价格进行折算.本文探究了2002年—2017年中国30个省份的水资源利用效率,以水权交易试点建立的时间为分界线,划分了两个时间段,水权交易试点前:2002年—2013年,水权交易试点后:2014年—2017年.

2.2 水权交易市场的竞合关系变化

水权交易市场实施前主体间竞合关系如表2所示,主体间选择相同的策略收益最大,即加入联盟会得到高的评价,不加入联盟则都会选择低的评价.

表2 水权交易实施之前决策单元间的策略

政策实施后,主体之间的合作与竞争关系由于试点地区的政绩比拼和政策考核而发生了变化.试点地区不仅要考核效率的提升,而且还要考虑效率排名的上升.水权交易市场实施后的关系如表3所示,(低,低)的收益是(1,1),(低,高)的收益是(1,0),(高,低)的收益是(0,1),(高,高)的收益可能存在四个值(0,0)、(0,1)、(1,0)和(1,1).类型1～类型3的均衡策略是(低,低).类型4存在两个均衡策略(高,高)和(低,低).一方面假如存在试点地区B(非试点地区A)对非试点地区A(试点地区B)的最大他评和最小他评一致的情况,那么由于政绩的比拼和加入联盟后收益并没有增加,非试点地区A(试点地区B)会更倾向于给试点地区B(非试点地区A)低的评价,这种情况下,(高,高)为均衡点的情况不会出现,即类型4的情况不存在.同时,因为试点地区内部存在着水资源交易的束缚,一旦试点地区B与非试点地区A之间的评价都是低的,那么试点地区的其他决策单元会由于水交易而捆绑在一起,因此,试点地区对非试点地区会形成统一的低评价.另一方面,西部试点地区水资源利用效率低[18],假如效率排名靠前的非试点地区加入联盟后,若联盟利益增加,则在联盟分配收益时,基于公平原则下的最小、最大交叉效率基础上,将对其增加一部分收益分配,这对效率排名末尾的试点地区不利,加剧了排名的差异,因此,试点地区会对非试点地区进行低评价.综上,试点地区与非试点地区的相互评价都是低评价.

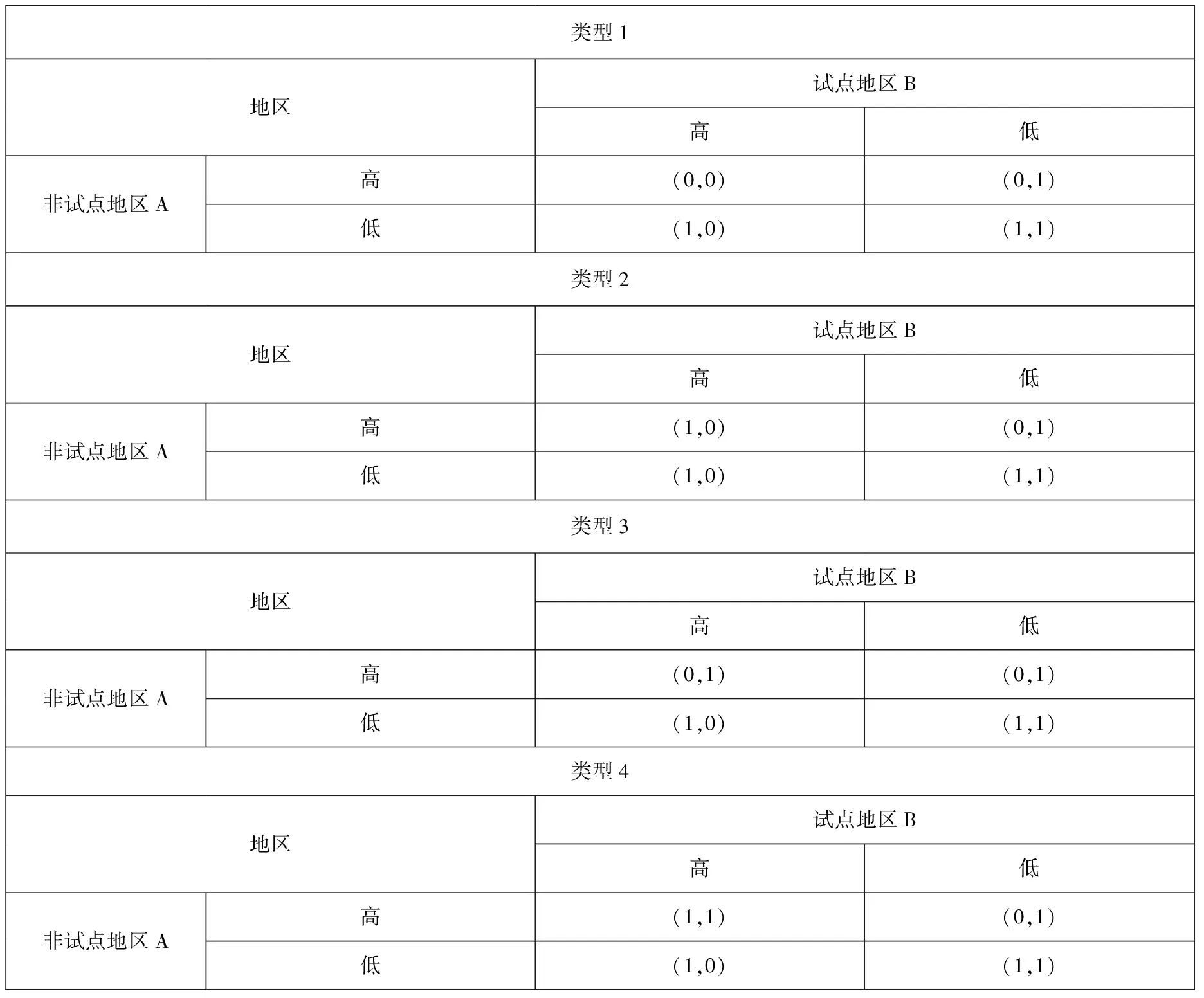
表3 水权交易实施后决策单元间的博弈类型

水权交易市场运行前,各主体之间的竞合关系是不确定的,可以是合作的关系而选择(高,高)的策略,也可以是竞争的关系而选择(低,低)的策略.为此,本文基于合作博弈的视角,利用Shapley值探究水资源利用效率,联盟内各主体之间的评价为(高,高),而联盟内的主体和联盟外的主体之间的评价为(低,低)的策略.水权交易市场运行后,该政策的实施影响了各地区竞合关系的变化,而竞合关系的演变又会通过最大、最小效率矩阵影响最终的评价,为此,本文通过比较竞合关系演变所带来的效率差异来验证水权交易市场的有效性.

2.3 水权交易市场的有效性分析

水权交易市场实施改变了地区间之前的竞合关系,而效率的差异体现了水权交易市场的影响.水权交易市场运行前,各地区水资源利用效率采用合作博弈的Shapley值求解,各地区组成相应的合作团体,团体内部的相互评价都是最大值,团体之间的相互评价都是最小值;运行后,所有地区被分成2个以上的团体,分别是国家试点地区、省级试点地区和非试点地区组成的团体.

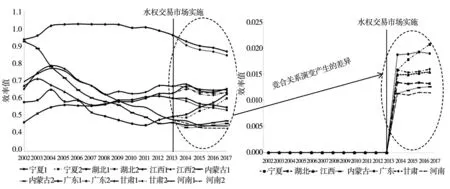
如图1所示,本文首先考察了水权交易市场对国家试点地区的影响,国家试点地区水资源利用效率的平均值由于竞合关系演变提升最大,且效率差异还在逐年增加;其次考察了省级试点地区受到的影响,省级试点地区效率的平均值相比于原来竞合关系的效率均值提升幅度小于国家试点地区;最后考察了非试点地区受到的影响,非试点地区效率的平均值在竞合关系发生变化后并没有迅速得到提升,但也受到了正向的影响,差异值在2015年达到了最大.本文与相关学者的结论相似[18, 39],验证了水权交易市场的有效性.综合来看,水权交易市场的运行能够有效地提高试点地区的水资源利用效率,同时,对非试点地区的水资源利用效率也具有溢出效应.

图1 水权交易市场实施后,竞合关系演变引起的效率变

从各地区的差异来看,如图2所示,地区1表示竞合关系发生变化的水资源利用效率,地区2表示竞合关系保持不变的水资源利用效率.本文首先考察了国家试点地区水资源利用效率的提升情况.如图2(a)所示,水权交易市场运行后,国家试点各地区的水资源利用效率在竞合关系演变后都得到了提升,说明水权交易市场对国家试点所有地区的水资源利用效率的提升有显著作用,同时,效率的差异非常明显,其中,宁夏和广东差异最大,说明水权交易市场对这两个省效率的提升最大;其次考察了省级试点各地区水资源利用效率的提升情况,如图2(b),水权交易市场运行后,省级试点地区水资源利用效率全部都得到了提升,同时,竞合关系所引致的效率差异大,其中,山东最大,浙江次之;最后考察了非试点地区水资源利用效率的情况,如图2(c)所示,水权交易市场引发竞合关系变化后,非试点地区的水资源利用效率大部分小于之前竞合关系不变的效率,这说明水权交易市场运行后,这些非试点地区的水资源利用效率低于之前竞合模式的效率,因此,全面推广水权交易市场、推进地区间合作交易可以起到提高效率的效果.

(a)国家试点各地区的效率值比较(1) 地区1表示竞合关系变化的效率值;地区2表示竞合关系不变的效率值.

3 结束语

对决策单元的评价与选择是一个相对复杂的过程,不仅需要考虑主体的自评和他评,也要考虑主体之间的竞合关系.以往的研究大多侧重决策单元间稳定竞合关系,但在复杂博弈情境下,决策单元间竞合关系会随着外界的冲击发生动态的演变.因此,本文提出了分层博弈交叉效率评价方法,在考虑外界冲击的情况下,探索了主体策略选择所导致的竞合关系的变化,进而影响效率的变化,同时,从公平的视角,重新分配了权重,并通过算例分析验证了方法的可行性,将决策单元间动态的竞合关系纳入效率评价框架更具现实意义.

具体来说,本文基于分层博弈交叉效率评价方法,分析了竞合关系演变所引致的水资源利用效率的差异,评价了水权交易市场的有效性,结果显示:地区间竞合关系演变通过效率评价矩阵影响最终效率,验证了水权交易市场的运行能够提高水资源利用效率,其中国家级试点地区的提升最大,省级试点地区次之,最后是非试点地区,并且该市场具有外溢效应.

政策评价问题是政策研究领域的重要课题,试点政策的实施通常会引起主体间竞合关系变化.本文提出的评价体系在碳市场、电价改革等政策评价领域具有重要应用价值.同时,本文也存在以下局限性,在研究政策冲击的效果时,仅探究了一种政策对主体之间博弈关系的影响,在未来研究中,将进一步探究考虑多种政策冲击所引致的竞合关系变化而带来的效率差异.